第二十二章二次函数求二次函数解析式专项练(含答案)2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 第二十二章二次函数求二次函数解析式专项练(含答案)2024--2025学年上学期初中数学人教版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 460.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览



文档简介
第二十二章 二次函数 求二次函数解析式 专项练
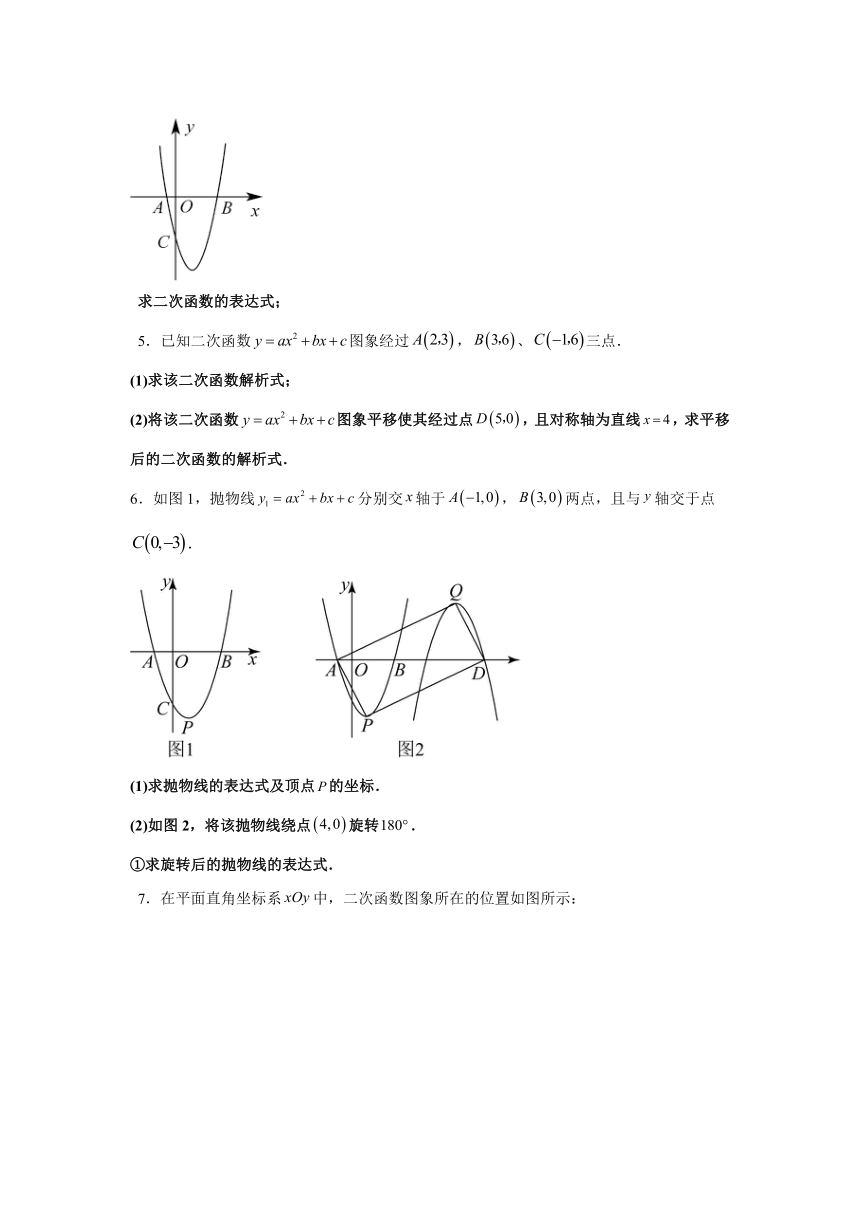
1.如图,抛物线,过,,三点,其中D为顶点,对称轴为直线.
求抛物线的解析式;
2.已知抛物线经过点和点.
求此抛物线的解析式及顶点坐标;
3.如图,已知拋物线的顶点坐标是,且与轴交于,两点,与轴交于点,点是直线下方抛物线上的一个动点,过点作轴,交于点,作于点.设点的横坐标为.
求抛物线的表达式.
4.如图,二次函数的图象与轴交于,两点,与轴交于点.
求二次函数的表达式;
5.已知二次函数图象经过,、三点.
(1)求该二次函数解析式;
(2)将该二次函数图象平移使其经过点,且对称轴为直线,求平移后的二次函数的解析式.
6.如图1,抛物线分别交轴于,两点,且与轴交于点.
(1)求抛物线的表达式及顶点的坐标.
(2)如图2,将该抛物线绕点旋转.
①求旋转后的抛物线的表达式.
7.在平面直角坐标系中,二次函数图象所在的位置如图所示:
请根据图象信息求该二次函数的表达式;
8.如图,在平面直角坐标系中,点,的坐标分别为、,经过、作轴的垂线分别交于、两点,得到正方形,抛物线经过,两点,点为抛物线上一点(不与点重合),过点分别作轴交轴于点,轴交轴于点,设点的横坐标为,
求抛物线的解析式
9.如图,直线与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且,抛物线经过A,B,C三点.
求抛物线的表达式;
10.如图,在平面直角坐标系中,已知点B的坐标为,且,抛物线图像经过A,B,C三点.
(1)求A,C两点的坐标;
(2)求抛物线的解析式;
参考答案:
解:将,,代入,
,
解得,
;
解析式为:;顶点坐标为
解:将点和点代入中得,
,解得:,
∴,
∵,
∴顶点坐标为;
拋物线的顶点坐标是,
,
将的坐标代入得,,
解得,
,
即;
二次函数的解析式为;
解:二次函数的表达式为,
把代入得,
解得,
∴二次函数的表达式为;
5.(1);
(2).
(1)解:把,、代入,
得:,
解得:,
∴该二次函数的解析式为;
(2)解:若将该二次函数图象平移后经过点,且对称轴为直线,
设平移后的二次函数的解析式为,
将点代入,得,
解得,.
∴将二次函数的图象平移后的二次函数的解析式为.
6.(1),
(2) ;
(1)解:由题意可设二次函数的表达式为,将点代入得,
∴二次函数表达式为,
∴顶点的坐标为.
(2)解:①设旋转后抛物线的顶点坐标为,
∵为顶点和的中点,即,,
∴点的坐标为,
∵旋转前后图形的形状不变,开口相反,
∴,
故旋转后的抛物线表达式为;
由图象可知二次函数图象过点,,,
设该二次函数的表达式为,
代入点得,
解得,
该二次函数的表达式为,即;
;
解:∵,轴于,
∴,
将点,代入中得:
,
∴,
∴抛物线所对应的函数表达式为.
解:由,当时,;当时,,
∴,
∴,
∴,
∴,
把代入抛物线中得:
,
解得:,
∴抛物线的解析式为;
10.(1)
(2)
(1)解:∵点B的坐标为,
∴,
∵,
∴,
∴;
(2)解:设该抛物线的表达式为,
把点代入得:,
把点代入得:,
解得:,
∴该抛物线的解析式为:,
1.如图,抛物线,过,,三点,其中D为顶点,对称轴为直线.
求抛物线的解析式;
2.已知抛物线经过点和点.
求此抛物线的解析式及顶点坐标;
3.如图,已知拋物线的顶点坐标是,且与轴交于,两点,与轴交于点,点是直线下方抛物线上的一个动点,过点作轴,交于点,作于点.设点的横坐标为.
求抛物线的表达式.
4.如图,二次函数的图象与轴交于,两点,与轴交于点.
求二次函数的表达式;
5.已知二次函数图象经过,、三点.
(1)求该二次函数解析式;
(2)将该二次函数图象平移使其经过点,且对称轴为直线,求平移后的二次函数的解析式.
6.如图1,抛物线分别交轴于,两点,且与轴交于点.
(1)求抛物线的表达式及顶点的坐标.
(2)如图2,将该抛物线绕点旋转.
①求旋转后的抛物线的表达式.
7.在平面直角坐标系中,二次函数图象所在的位置如图所示:
请根据图象信息求该二次函数的表达式;
8.如图,在平面直角坐标系中,点,的坐标分别为、,经过、作轴的垂线分别交于、两点,得到正方形,抛物线经过,两点,点为抛物线上一点(不与点重合),过点分别作轴交轴于点,轴交轴于点,设点的横坐标为,
求抛物线的解析式
9.如图,直线与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且,抛物线经过A,B,C三点.
求抛物线的表达式;
10.如图,在平面直角坐标系中,已知点B的坐标为,且,抛物线图像经过A,B,C三点.
(1)求A,C两点的坐标;
(2)求抛物线的解析式;
参考答案:
解:将,,代入,
,
解得,
;
解析式为:;顶点坐标为
解:将点和点代入中得,
,解得:,
∴,
∵,
∴顶点坐标为;
拋物线的顶点坐标是,
,
将的坐标代入得,,
解得,
,
即;
二次函数的解析式为;
解:二次函数的表达式为,
把代入得,
解得,
∴二次函数的表达式为;
5.(1);
(2).
(1)解:把,、代入,
得:,
解得:,
∴该二次函数的解析式为;
(2)解:若将该二次函数图象平移后经过点,且对称轴为直线,
设平移后的二次函数的解析式为,
将点代入,得,
解得,.
∴将二次函数的图象平移后的二次函数的解析式为.
6.(1),
(2) ;
(1)解:由题意可设二次函数的表达式为,将点代入得,
∴二次函数表达式为,
∴顶点的坐标为.
(2)解:①设旋转后抛物线的顶点坐标为,
∵为顶点和的中点,即,,
∴点的坐标为,
∵旋转前后图形的形状不变,开口相反,
∴,
故旋转后的抛物线表达式为;
由图象可知二次函数图象过点,,,
设该二次函数的表达式为,
代入点得,
解得,
该二次函数的表达式为,即;
;
解:∵,轴于,
∴,
将点,代入中得:
,
∴,
∴抛物线所对应的函数表达式为.
解:由,当时,;当时,,
∴,
∴,
∴,
∴,
把代入抛物线中得:
,
解得:,
∴抛物线的解析式为;
10.(1)
(2)
(1)解:∵点B的坐标为,
∴,
∵,
∴,
∴;
(2)解:设该抛物线的表达式为,
把点代入得:,
把点代入得:,
解得:,
∴该抛物线的解析式为:,
同课章节目录
