2024-2025学年人教版数学八上 第十三章 轴对称 单元试卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学八上 第十三章 轴对称 单元试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 488.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 10:25:45 | ||
图片预览



文档简介
2024-2025学年人教版数学八上 第十三章 轴对称 单元试卷
一、单选题
1.下列图形中,是中心对称的图形是( )
A.B.C. D.
2.在平面直角坐标系中,点关于轴的对称点的坐标为( )
A. B. C. D.
3.等腰三角形三边中有两边的长分别是4和9,则这个等腰三角形的周长是( )
A.17 B.22 C.17或22 D.不能确定
4.等腰三角形一内角为,则底角度数是( )
A.或 B. C. D.
5.如图,在中,与的平分线交于点I,过点I作交于点D,交于点E,且,,,则下列说法错误的是( ).
A.和是等腰三角形 B.
C.的周长是8 D.
6.如图,中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,的周长为9cm,则的周长是( )
A.12cm B.15cm C.21cm D.18cm
7.如图,在中,,将沿直线m翻折,点B落在点D的位置,则的度数是( )
A. B. C. D.
8.图,在△ABC中,,分别以点A、C为圆心,大于的长为半径作弧,两弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连接AE,若,则( )
A. B. C. D.
9.如图,等边三角形的边长为2,A、B、三点在一条直线上,且.若D为线段上一动点,则的最小值是( )
A.3 B.4 C.5 D.6
10.如图,,点C在上,且.按下列要求画图:以C为圆心,1为半径向右画弧交于点,得第1条线段;再以为圆心,1为半径向右画弧交于点,得第2条线段;再以为圆心,1为半径向右画弧交于点,得第3条线段;…;这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值为( )
A.7 B.8 C.9 D.10
二、填空题
11.一个等腰三角形的两边长分别是2cm和4cm,则第三边长为 cm.
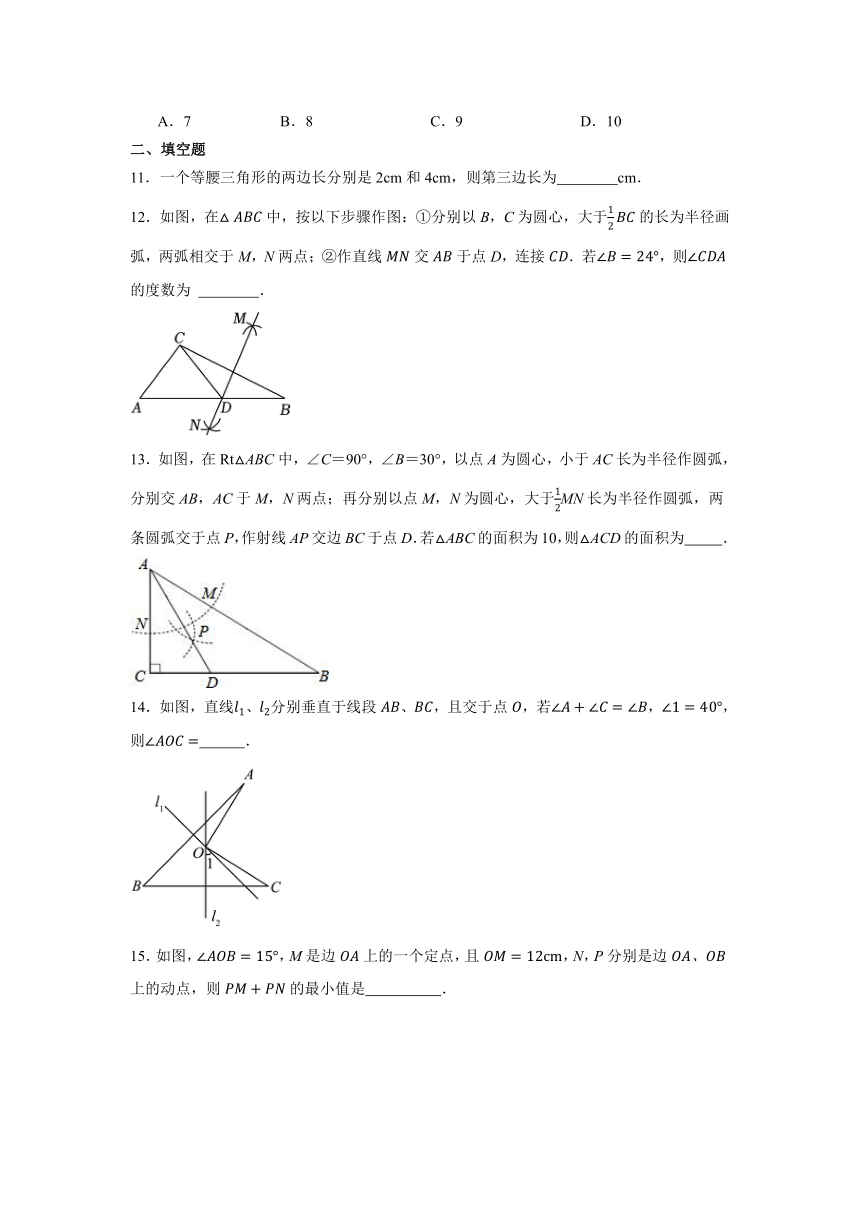
12.如图,在中,按以下步骤作图:①分别以B,C为圆心,大于的长为半径画弧,两弧相交于M,N两点;②作直线交于点D,连接.若,则的度数为 .
13.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于M,N两点;再分别以点M,N为圆心,大于MN长为半径作圆弧,两条圆弧交于点P,作射线AP交边BC于点D.若△ABC的面积为10,则△ACD的面积为 .
14.如图,直线、分别垂直于线段、,且交于点,若,,则 .
15.如图,,M是边上的一个定点,且,N,P分别是边上的动点,则的最小值是 .
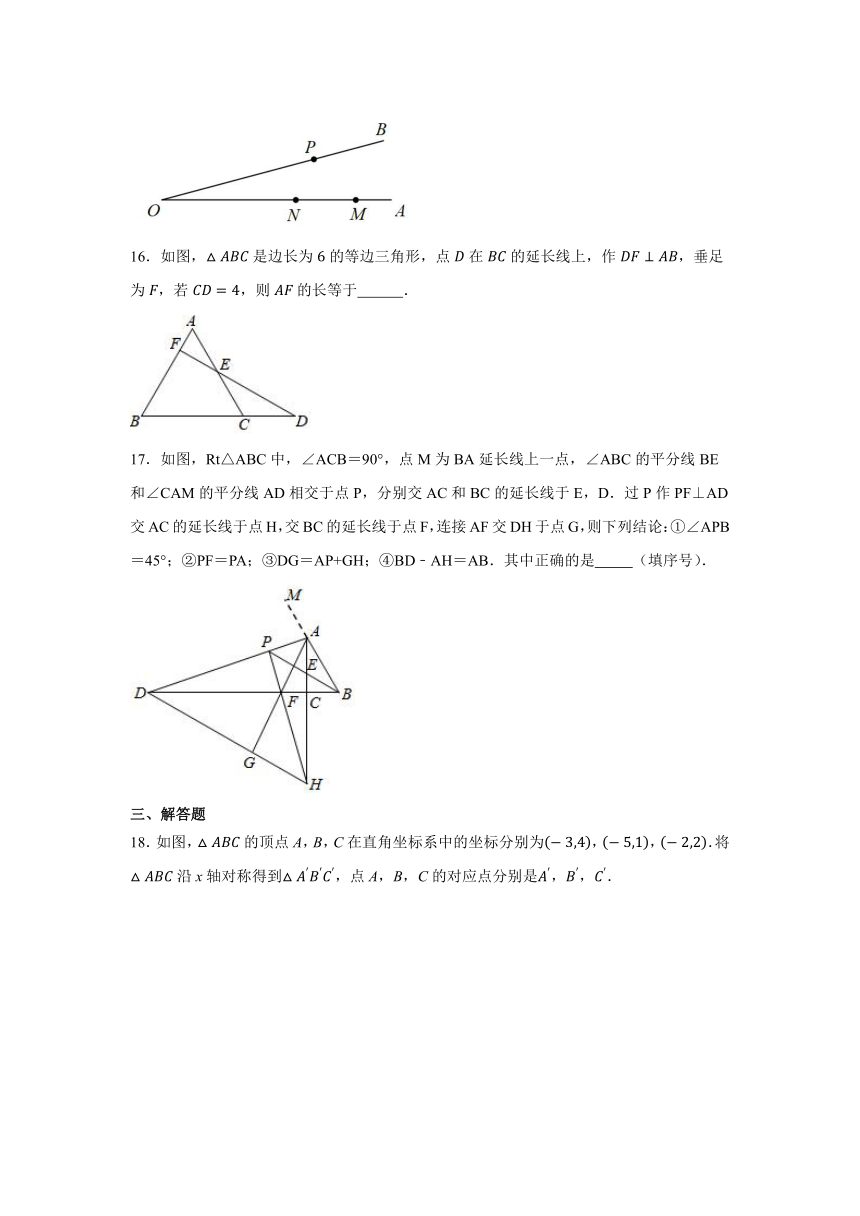
16.如图,是边长为的等边三角形,点在的延长线上,作,垂足为,若,则的长等于 .
17.如图,Rt△ABC中,∠ACB=90°,点M为BA延长线上一点,∠ABC的平分线BE和∠CAM的平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G,则下列结论:①∠APB=45°;②PF=PA;③DG=AP+GH;④BD﹣AH=AB.其中正确的是 (填序号).
三、解答题
18.如图,的顶点A,B,C在直角坐标系中的坐标分别为,,.将沿x轴对称得到,点A,B,C的对应点分别是,,.
(1)请在图中画出;
(2)若点是内部一点,则点P经过上述变换后的对应点的坐标为(______,______).
19.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为10,求BC的长.
20.如图,在中,,,点D是的中点,点E为边上一点,连接,,以为边在的左侧作等边三角形,连接.
(1)求证:为等边三角形;
(2)求证:.
21.如图,点是等边内一点,,.以为一边作等边三角形,连接、.
(1)求证:;
(2)当时,试判断的形状,并说明理由;
(3)当是等腰三角形时,求的度数.
22.在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以BD为一边且在BD的下方作等边△BDE,连接CE.
(1)在图1中,若D与M重合时,则∠BCE= 度;
(2)在图2中,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AC=10,试求BE的长.
23.已知Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,∠ADE=∠AED=45°,连接CF.
(1)发现问题
如图①,当点D在边BC上时.
①请写出BD和CE之间的数量关系为 ,位置关系为 ;
②求证:CE+CD=BC
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中BC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,不证明.
(3)拓展延伸
如图③,当点D在CB的延长线上且其他条件不变时,若BC=6,CE=2,求线段CD的长.
参考答案:
1.B
2.A
3.B
4.D
5.B
6.B
7.C
8.B
9.B
10.B
11.4
12.
13.
14.
15.
16.
17.①②④
18.(1)解:如图所示:即为所求;
(2)解:∵沿x轴对称得到,点,
∴点,
19.(1)∠BAC=180﹣∠ABC﹣∠ACB=180﹣30﹣50=100,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30,
∵FG是AC的垂直平分线,
∴FA=FC,
∴∠FAC=∠ACB=50,
∴∠DAF=∠BAC﹣(∠DAB+∠FAC)=20;
(2)∵△DAF的周长为10,
∴AD+DF+FC=10,
∴BC=BD+DF+FC=AD+DF+FC=10.
20.(1)证明:∵在中,,,
∴,,
又∵点D是的中点,
∴,
∴,
∴为等腰三角形,
又∵,
∴为等边三角形;
(2)证明:由(1)可知为等边三角形,
∴,
∵为等边三角形,
∴,
∴,
∴ ,
即,
在和中,
,
∴ ,
∴.
21.(1)和是等边三角形,
,,,,
,
,
在和中
,
;
(2)是直角三角形.
是等边三角形,
,
是等边三角形,
,
,
,
,
,
,,
,
是直角三角形;
(3),,,,
①当时,,
,
;
②当时,,
,
;
③当时,,
,
.
所以,当为、、时,是等腰三角形.
22.(1)如图1,∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=CD,∠BAD=∠BAC=30°,
∵△BDE是等边三角形,
∴∠BDE=60°,BD=DE,
在△ABD和△BCE中,
∵AB=BC,∠ABD=∠CBE,BD=BE,
∴△ABD≌△CBE,
∴∠BCE=∠BAD=30°;
(2)(1)中的结论成立.理由如下:
如图2,∵△ABC和△BDE均为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE.
在△ABD与△CBE中,
∵AB=BC,∠ABD=∠CBE,BD=BE,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∵在等边△ABC中,M是BC中点.
∴∠BAD=∠BAC=30°,
∴∠BCE=30°;
(3)如图1,∵在等边△ABC中,AC=10,
∴BC=AC=10.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=BC=5,
∵△BDE是等边三角形,
∴BE=BD=5.
23.(1)解:①BD=CE,BD⊥CE.
∵∠ABC=∠ACB=45°,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
∵
∴,
∴BD=CE,∠ACE=∠B=45°,
∴∠BCE=90°,即BD⊥CE,
故答案为:BD=CE;BD⊥CE.
②证明:∵BD=CE,
∴BC=BD+CD=CE+CD.
(2)解:(1)中BC、CE、CD之间存在的数量关系不成立,新的数量关系是CE=BC+CD.
证明:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
∵
∴,
∴BD=CE,
∴CE=BC+CD.
(3)解:由(1)、(2)可知∠BAD=∠CAE,
在△BAD和△CAE中,
∵
∴,
∴
∴
∴的长为8.
一、单选题
1.下列图形中,是中心对称的图形是( )
A.B.C. D.
2.在平面直角坐标系中,点关于轴的对称点的坐标为( )
A. B. C. D.
3.等腰三角形三边中有两边的长分别是4和9,则这个等腰三角形的周长是( )
A.17 B.22 C.17或22 D.不能确定
4.等腰三角形一内角为,则底角度数是( )
A.或 B. C. D.
5.如图,在中,与的平分线交于点I,过点I作交于点D,交于点E,且,,,则下列说法错误的是( ).
A.和是等腰三角形 B.
C.的周长是8 D.
6.如图,中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,的周长为9cm,则的周长是( )
A.12cm B.15cm C.21cm D.18cm
7.如图,在中,,将沿直线m翻折,点B落在点D的位置,则的度数是( )
A. B. C. D.
8.图,在△ABC中,,分别以点A、C为圆心,大于的长为半径作弧,两弧相交于点M、N,作直线MN,分别交AC、BC于点D、E,连接AE,若,则( )
A. B. C. D.
9.如图,等边三角形的边长为2,A、B、三点在一条直线上,且.若D为线段上一动点,则的最小值是( )
A.3 B.4 C.5 D.6
10.如图,,点C在上,且.按下列要求画图:以C为圆心,1为半径向右画弧交于点,得第1条线段;再以为圆心,1为半径向右画弧交于点,得第2条线段;再以为圆心,1为半径向右画弧交于点,得第3条线段;…;这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值为( )
A.7 B.8 C.9 D.10
二、填空题
11.一个等腰三角形的两边长分别是2cm和4cm,则第三边长为 cm.
12.如图,在中,按以下步骤作图:①分别以B,C为圆心,大于的长为半径画弧,两弧相交于M,N两点;②作直线交于点D,连接.若,则的度数为 .
13.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于M,N两点;再分别以点M,N为圆心,大于MN长为半径作圆弧,两条圆弧交于点P,作射线AP交边BC于点D.若△ABC的面积为10,则△ACD的面积为 .
14.如图,直线、分别垂直于线段、,且交于点,若,,则 .
15.如图,,M是边上的一个定点,且,N,P分别是边上的动点,则的最小值是 .
16.如图,是边长为的等边三角形,点在的延长线上,作,垂足为,若,则的长等于 .
17.如图,Rt△ABC中,∠ACB=90°,点M为BA延长线上一点,∠ABC的平分线BE和∠CAM的平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G,则下列结论:①∠APB=45°;②PF=PA;③DG=AP+GH;④BD﹣AH=AB.其中正确的是 (填序号).
三、解答题
18.如图,的顶点A,B,C在直角坐标系中的坐标分别为,,.将沿x轴对称得到,点A,B,C的对应点分别是,,.
(1)请在图中画出;
(2)若点是内部一点,则点P经过上述变换后的对应点的坐标为(______,______).
19.如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
(1)求∠DAF的度数;
(2)若△DAF的周长为10,求BC的长.
20.如图,在中,,,点D是的中点,点E为边上一点,连接,,以为边在的左侧作等边三角形,连接.
(1)求证:为等边三角形;
(2)求证:.
21.如图,点是等边内一点,,.以为一边作等边三角形,连接、.
(1)求证:;
(2)当时,试判断的形状,并说明理由;
(3)当是等腰三角形时,求的度数.
22.在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以BD为一边且在BD的下方作等边△BDE,连接CE.
(1)在图1中,若D与M重合时,则∠BCE= 度;
(2)在图2中,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AC=10,试求BE的长.
23.已知Rt△ABC中,AB=AC,∠ABC=∠ACB=45°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,∠ADE=∠AED=45°,连接CF.
(1)发现问题
如图①,当点D在边BC上时.
①请写出BD和CE之间的数量关系为 ,位置关系为 ;
②求证:CE+CD=BC
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中BC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,不证明.
(3)拓展延伸
如图③,当点D在CB的延长线上且其他条件不变时,若BC=6,CE=2,求线段CD的长.
参考答案:
1.B
2.A
3.B
4.D
5.B
6.B
7.C
8.B
9.B
10.B
11.4
12.
13.
14.
15.
16.
17.①②④
18.(1)解:如图所示:即为所求;
(2)解:∵沿x轴对称得到,点,
∴点,
19.(1)∠BAC=180﹣∠ABC﹣∠ACB=180﹣30﹣50=100,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠ABC=30,
∵FG是AC的垂直平分线,
∴FA=FC,
∴∠FAC=∠ACB=50,
∴∠DAF=∠BAC﹣(∠DAB+∠FAC)=20;
(2)∵△DAF的周长为10,
∴AD+DF+FC=10,
∴BC=BD+DF+FC=AD+DF+FC=10.
20.(1)证明:∵在中,,,
∴,,
又∵点D是的中点,
∴,
∴,
∴为等腰三角形,
又∵,
∴为等边三角形;
(2)证明:由(1)可知为等边三角形,
∴,
∵为等边三角形,
∴,
∴,
∴ ,
即,
在和中,
,
∴ ,
∴.
21.(1)和是等边三角形,
,,,,
,
,
在和中
,
;
(2)是直角三角形.
是等边三角形,
,
是等边三角形,
,
,
,
,
,
,,
,
是直角三角形;
(3),,,,
①当时,,
,
;
②当时,,
,
;
③当时,,
,
.
所以,当为、、时,是等腰三角形.
22.(1)如图1,∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=CD,∠BAD=∠BAC=30°,
∵△BDE是等边三角形,
∴∠BDE=60°,BD=DE,
在△ABD和△BCE中,
∵AB=BC,∠ABD=∠CBE,BD=BE,
∴△ABD≌△CBE,
∴∠BCE=∠BAD=30°;
(2)(1)中的结论成立.理由如下:
如图2,∵△ABC和△BDE均为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE.
在△ABD与△CBE中,
∵AB=BC,∠ABD=∠CBE,BD=BE,
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,
∵在等边△ABC中,M是BC中点.
∴∠BAD=∠BAC=30°,
∴∠BCE=30°;
(3)如图1,∵在等边△ABC中,AC=10,
∴BC=AC=10.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=BC=5,
∵△BDE是等边三角形,
∴BE=BD=5.
23.(1)解:①BD=CE,BD⊥CE.
∵∠ABC=∠ACB=45°,∠ADE=∠AED=45°,
∴∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
∵
∴,
∴BD=CE,∠ACE=∠B=45°,
∴∠BCE=90°,即BD⊥CE,
故答案为:BD=CE;BD⊥CE.
②证明:∵BD=CE,
∴BC=BD+CD=CE+CD.
(2)解:(1)中BC、CE、CD之间存在的数量关系不成立,新的数量关系是CE=BC+CD.
证明:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
∵
∴,
∴BD=CE,
∴CE=BC+CD.
(3)解:由(1)、(2)可知∠BAD=∠CAE,
在△BAD和△CAE中,
∵
∴,
∴
∴
∴的长为8.
