人教版六年级数学上册第四单元综合复习练习题(含答案)
文档属性
| 名称 | 人教版六年级数学上册第四单元综合复习练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 848.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 19:47:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版六年级数学上册第四单元综合复习练习题(含答案)
一、填空题(第1题4分,其余每题2分,共26分)
1. ( )÷4==( ):28=0.75=
2.若a÷b=0.625,则b:a=( ):( ),b比a多。
3.一辆汽车从甲地开往乙地,小时行驶了80千米,这辆汽车行驶的路程与时间比值是( ),这个比值表示的意义是( )。
4.甲、乙、丙三个数的平均数是150,甲、乙、丙三数的比是4:5:6,乙数是( )。
5.甲、乙两列火车的速度比是5:6,甲车行驶的路时间比乙车少,那么这两列火车行驶的路程( ):( )。
6.甲、乙两辆汽车同时从A、B两地出发,相向而行,6小时相遇,甲车再行4小时即可到达B地。那么乙车再行( )小时到达A地。
7.如图所示,一个底面是正方形的长方体,其侧面积是1200平方厘米,底面边长与高之比是1:3。那么这个长方体的体积是( )立方厘米。
8.如图所示,大小正方形中阴影部分的面积比是3:2,那么大小正方形中空白部分的面积比是( ):( )。
9.如图所示,由4个完全相同的小长方形拼成一个大长方形,已知大长方形的周长是56dm,则每个 小长方形的面积是( )dm2。
10.一个等腰三角形中两条边的长度之比为1:2,这两条边的长度相差2cm,这个等腰三角形的周长是( )cm。
11.今年王老师与聪聪的年龄比是7:3,再过5年,王老师与聪聪的年龄比2:1,今年王老师与聪聪的年龄分别是( )、( )岁。
12. 一个分数的分子和分母的和是18,如果将分子加上8,分母加上9,新的分数约分后是,那么原来的分数是( )。
二、选择题(10分)
13.甲与乙的比是4:5那些说法正确的是( )。
A. 甲比乙少 B.乙比甲多 C.甲占甲、乙之和的 D.乙占甲、乙之和的
14.被减数、减数与差三数之和是32,减数与差的比是5:3,这差是( )。
A.6 B.12 C.32
15.在正方形ABCD中,已知BE:EC=1:2,三角形DEC的面积占总面积的。
A. B. C. D.
16.小明花了40元买了2本笔记本和4支钢笔,笔记本和钢笔的单价比是1:2,笔记本和钢笔的单价分别是( )。
A.1元和2元 B.2元和4元 C.4元和8元 D.8元和10元。
17.甲、乙两根铁棒竖直插入圆柱体容器中,甲棒露在容器外面,乙棒露在容器外面,则甲、乙两根铁棒的长度之比为( )。
A.3:5 B.5:6 C.9:10 D.9:15
三、计算题(24分)
18.化简比(6分)
0.375: :2 3时45分:50分钟
19.脱式计算(能简算用简算)(9分)
45×+43× (-+)÷ 2024×
20.解方程(9分)
:x= x:0.25 = 13:(x+5)=
四、操作题(3+3=6分)
涂一涂,使涂色部分和未涂色部分方格数的比是5:3,并说一说你是怎样理解“涂色部分和未涂色部分方格数的比是5:3”的。
我的想法:
五、解决问题(6+6+7+7+8=34分)
21.聪聪打算自制蜂蜜水,他往15克的蜂蜜原料中加入60克水后,发现一份调制说明书(如下图)。请帮聪聪判断:为了使口感最佳,应往已调制的蜂蜜水中加水还是加蜂蜜原料?应加多少克?
22.白棋子比黑棋子多18枚,将黑白棋子各加上1枚后,黑棋子正好是白棋子的比是1:3。现在黑白棋子共有多少枚?
23.聪聪读一本书,第一天读了全书的,第二天再读了18页,这时已读与未读的页数之比是3:2。这本书共有多少页?
24.水果店共运进 114 筐水果,香蕉筐数的、梨的筐数的与苹果筐数的相等.这三种水果各有多少筐
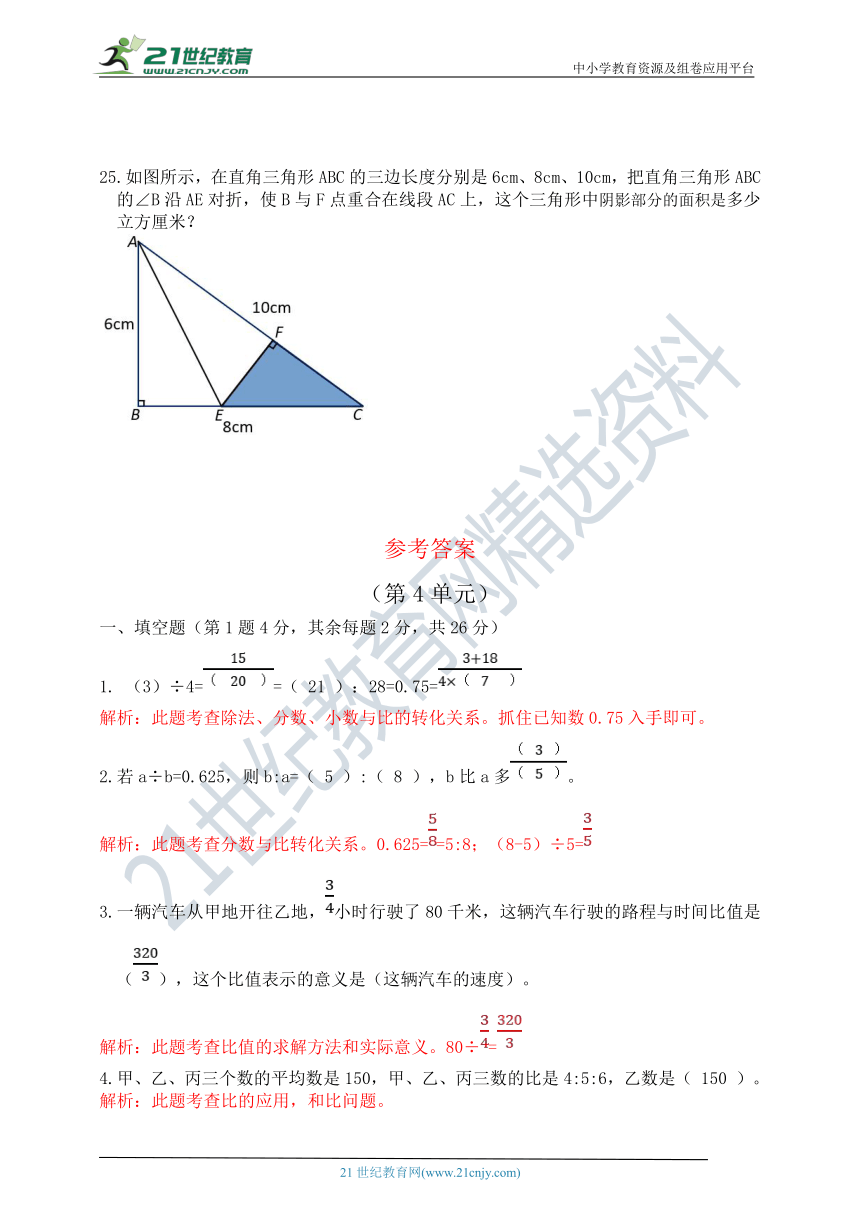
25.如图所示,在直角三角形ABC的三边长度分别是6cm、8cm、10cm,把直角三角形ABC的∠B沿AE对折,使B与F点重合在线段AC上,这个三角形中阴影部分的面积是多少立方厘米?
参考答案
(第4单元)
一、填空题(第1题4分,其余每题2分,共26分)
1. (3)÷4==( 21 ):28=0.75=
解析:此题考查除法、分数、小数与比的转化关系。抓住已知数0.75入手即可。
2.若a÷b=0.625,则b:a=( 5 ):( 8 ),b比a多。
解析:此题考查分数与比转化关系。0.625==5:8;(8-5)÷5=
3.一辆汽车从甲地开往乙地,小时行驶了80千米,这辆汽车行驶的路程与时间比值是(),这个比值表示的意义是(这辆汽车的速度)。
解析:此题考查比值的求解方法和实际意义。80÷=
4.甲、乙、丙三个数的平均数是150,甲、乙、丙三数的比是4:5:6,乙数是( 150 )。
解析:此题考查比的应用,和比问题。
三个数的和是150×3=450,按比分配,乙数=450×=150
5.甲、乙两列火车的速度比是5:6,甲车行驶的路时间比乙车少,那么这两列火车行驶的路程( 5 ):( 18 )。
解析:此题考查复比问题,分数与比的转化关系。
速度比=5:6
时间比=(1-):1=1:3
路程比=(5×1):(6×3)=5:18
6.甲、乙两辆汽车同时从A、B两地出发,相向而行,6小时相遇,甲车再行4小时即可到达B地。那么乙车再行( 9 )小时到达A地。
解析:此题考查比的应用。
甲行驶4小时的路程相当于乙行驶6小时的路程。在里程相同的情况下,甲乙所用时间的比是4:6=(4+6):(6+9)
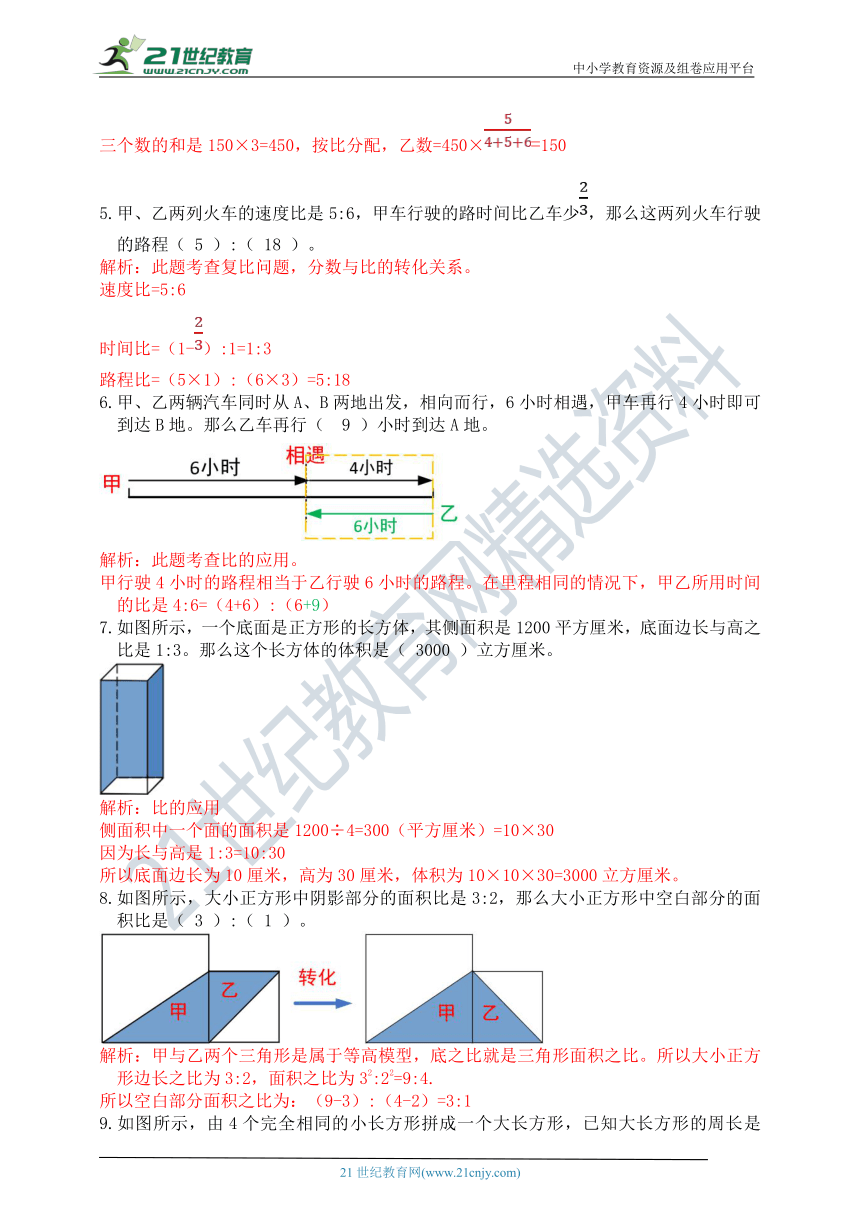
7.如图所示,一个底面是正方形的长方体,其侧面积是1200平方厘米,底面边长与高之比是1:3。那么这个长方体的体积是( 3000 )立方厘米。
解析:比的应用
侧面积中一个面的面积是1200÷4=300(平方厘米)=10×30
因为长与高是1:3=10:30
所以底面边长为10厘米,高为30厘米,体积为10×10×30=3000立方厘米。
8.如图所示,大小正方形中阴影部分的面积比是3:2,那么大小正方形中空白部分的面积比是( 3 ):( 1 )。
解析:甲与乙两个三角形是属于等高模型,底之比就是三角形面积之比。所以大小正方形边长之比为3:2,面积之比为32:22=9:4.
所以空白部分面积之比为:(9-3):(4-2)=3:1
9.如图所示,由4个完全相同的小长方形拼成一个大长方形,已知大长方形的周长是56dm,则每个 小长方形的面积是( 48 )dm2。
解析:通过我观察,很容易发现大长方形的长与宽的比是(3+1):3=4:3
长=56÷2×=16(厘米)
宽=56÷2-16=12(厘米)
小长方形面积=16×12÷4=48(cm2)
10.一个等腰三角形中两条边的长度之比为1:2,这两条边的长度相差2cm,这个等腰三角形的周长是( 10 )cm。
解析:考查比的应用和三角形三边关系两个知识点。
等腰三角形三边之比为1:1:2(1+1=2),不符合任意两边之和大于第三边三角形三边关系,不符合题意,舍去;应该为1:2:2、
得出等腰三角形周长=2÷(2-1)×(1+2+2)=10(cm)
11.今年王老师与聪聪的年龄比是7:3,再过5年,王老师与聪聪的年龄比2:1,今年王老师与聪聪的年龄分别是( 35 )、( 15 )岁。
解析:考查抓住不变量(年龄差不变)转化单位“1”问题。
解法一:
今年王老师的年龄相当于王老师与聪聪年龄差的,5年之后,王老师的年龄相当于王老师与聪聪年龄差的。
王老师与聪聪年龄差=5÷(-)=20(岁)
王老师年龄=20×=35(岁)
聪聪年龄=20×=15(岁)或35-20=15(岁)
解法二:
解:设王老师今年的年龄为x岁,则聪聪的年龄为x岁。
X+5=2(x+5)
X=35
聪聪x=×35=15(岁)
12. 一个分数的分子和分母的和是18,如果将分子加上8,分母加上9,新的分数约分后是,那么原来的分数是( )。
解析:分子与分母的和比问题。
(1)分子与分母的和是18+8+9=35;分子与分母之比为3:4.
(2)新分数的分子是35×=15,分母是35×=20,即现在的分数是
(3)15-8=7,20-9=11,所以,原来的分数是
二、选择题(10分)
13.甲与乙的比是4:5那些说法正确的是( C )。
A. 甲比乙少 B.乙比甲多 C.甲占甲、乙之和的 D.乙占甲、乙之和的
解析:考查比与分数关系转化
14.被减数、减数与差三数之和是32,减数与差的比是5:3,这差是( A )。
A.6 B.12 C.32
解析:考查减数与差的和倍问题:32÷2÷(5+3)×3=6
15.在正方形ABCD中,已知BE:EC=1:2,三角形DEC的面积占总面积的( A )。
A. B. C. D.
解析:采用分割法即可解答。
16.小明花了40元买了2本笔记本和4支钢笔,笔记本和钢笔的单价比是1:2,笔记本和钢笔的单价分别是( C )。
A.1元和2元 B.2元和4元 C.4元和8元 D.8元和10元。
解析:复比问题
笔记本和钢笔数量比2:4,单价比1:2,总价比(2×1):(4×2)=1:4。
笔记本总价=40÷(1+4)×1=8(元),单价8÷2=4(元)
钢笔单价=4×2=8(元)
17.甲、乙两根铁棒竖直插入圆柱体容器中,甲棒露在容器外面,乙棒露在容器外面,则甲、乙两根铁棒的长度之比为( C )。
A.3:5 B.5:6 C.9:10 D.9:15
解析:等式换比。甲棒和乙棒在容器里面部分长度相等。
即甲棒×(1-)=乙棒×(1-),设甲棒×=乙棒×=1
甲棒:乙棒=:=9:10
三、计算题(24分)
18.化简比(6分)
0.375: :2 3时45分:50分钟
=: =: =225分钟:50分钟
=25:32 =20:77 =9:2
19.脱式计算(能简算用简算)(9分)
45×+43× (-+)÷ 2024×
=(44+1)×+(44-1)× =(-+)×60 =(2023+)×
=44×(+)+- =45-24+10 =2022+1
=28.5 =31 =2023
20.解方程(9分)
:x= x:0.25 = 13:(x+5)=
解:x=÷ 解:x=0.25× 解:
X= x=
X=
四、操作题(3+3=6分)
涂一涂,使涂色部分和未涂色部分方格数的比是5:3,并说一说你是怎样理解“涂色部分和未涂色部分方格数的比是5:3”的。
我的想法:
我的想法:把方格总数平均分成8份,每份是3格,涂色部分占5份就是15格,未涂色部分占3份就是9格。(言之有理即可)
五、解决问题(6+6+7+7+8=34分)
21.聪聪打算自制蜂蜜水,他往15克的蜂蜜原料中加入60克水后,发现一份调制说明书(如下图)。请帮聪聪判断:为了使口感最佳,应往已调制的蜂蜜水中加水还是加蜂蜜原料?应加多少克?
解答:15:60=,>,15÷-60=40(g)
答:应往已调制的蜂蜜水中加水,应加40g。
22.白棋子比黑棋子多18枚,将黑白棋子各加上1枚后,黑棋子正好是白棋子的比是1:3。现在黑白棋子共有多少枚?
解析:差比问题。
差不变:将黑白棋子各加上1枚后,白棋子比黑棋子还是多18枚,且黑棋子正好是白棋子的比是1:3。
现在黑棋子=18÷(3-1)×1=9(枚)
现在白棋子=18÷(3-1)×3=27(枚)
现在一共9+27=36(枚)
答:(略)
23.聪聪读一本书,第一天读了全书的,第二天再读了18页,这时已读与未读的页数之比是3:2。这本书共有多少页?
解析:转化单位“1”。
把“这时已读与未读的页数之比是3:2”转化为“已读的页数占全书页数的”
根据量率对应关系:18页占全书的-。
列式:18÷(-)=80(页)
答:(略)
24.水果店共运进 114 筐水果,香蕉筐数的、梨的筐数的与苹果筐数的相等.这三种水果各有多少筐
解析:考查等式换比。
设:香蕉筐数×=梨的筐数×=苹果筐数×=1
所以香蕉:梨:苹果=(1÷):(1÷):(1÷)=6:8:5
114÷(6+8+5)=6(筐)
香蕉:6×6=36(筐)
梨:6×8=48(筐)
苹果:6×5=30(筐)
答:(略)
25.如图所示,在直角三角形ABC的三边长度分别是6cm、8cm、10cm,把直角三角形ABC的∠B沿AE对折,使B与F点重合在线段AC上,这个三角形中阴影部分的面积是多少立方厘米?
解析:
方法一:底高模型。
在△AEC中,△AEF和△FEC构成等高模型。两个三角形的面积之比就是底之比。
所以S△AEF:S△FEC=6:(10-6)=3:2;又因为△AEF和△AEB为重叠三角形,所以此两个三角形面积相等。所以S△AEB:S△AEF:S△FEC=3:3:2。所以阴影△EFC面积为△ABC面积的:
列式:6×8÷2×=6(cm2)
方法二:方程法
解:设BE=x,则EF=x.
根据关系式:S△ABE+S△AEC=S△ABC
得出方程:6x÷2+10x÷2=6×8÷2
3x+5x=24
X=3
所以S△EFC=(10-6)×3÷2=6(cm2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版六年级数学上册第四单元综合复习练习题(含答案)
一、填空题(第1题4分,其余每题2分,共26分)
1. ( )÷4==( ):28=0.75=
2.若a÷b=0.625,则b:a=( ):( ),b比a多。
3.一辆汽车从甲地开往乙地,小时行驶了80千米,这辆汽车行驶的路程与时间比值是( ),这个比值表示的意义是( )。
4.甲、乙、丙三个数的平均数是150,甲、乙、丙三数的比是4:5:6,乙数是( )。
5.甲、乙两列火车的速度比是5:6,甲车行驶的路时间比乙车少,那么这两列火车行驶的路程( ):( )。
6.甲、乙两辆汽车同时从A、B两地出发,相向而行,6小时相遇,甲车再行4小时即可到达B地。那么乙车再行( )小时到达A地。
7.如图所示,一个底面是正方形的长方体,其侧面积是1200平方厘米,底面边长与高之比是1:3。那么这个长方体的体积是( )立方厘米。
8.如图所示,大小正方形中阴影部分的面积比是3:2,那么大小正方形中空白部分的面积比是( ):( )。
9.如图所示,由4个完全相同的小长方形拼成一个大长方形,已知大长方形的周长是56dm,则每个 小长方形的面积是( )dm2。
10.一个等腰三角形中两条边的长度之比为1:2,这两条边的长度相差2cm,这个等腰三角形的周长是( )cm。
11.今年王老师与聪聪的年龄比是7:3,再过5年,王老师与聪聪的年龄比2:1,今年王老师与聪聪的年龄分别是( )、( )岁。
12. 一个分数的分子和分母的和是18,如果将分子加上8,分母加上9,新的分数约分后是,那么原来的分数是( )。
二、选择题(10分)
13.甲与乙的比是4:5那些说法正确的是( )。
A. 甲比乙少 B.乙比甲多 C.甲占甲、乙之和的 D.乙占甲、乙之和的
14.被减数、减数与差三数之和是32,减数与差的比是5:3,这差是( )。
A.6 B.12 C.32
15.在正方形ABCD中,已知BE:EC=1:2,三角形DEC的面积占总面积的。
A. B. C. D.
16.小明花了40元买了2本笔记本和4支钢笔,笔记本和钢笔的单价比是1:2,笔记本和钢笔的单价分别是( )。
A.1元和2元 B.2元和4元 C.4元和8元 D.8元和10元。
17.甲、乙两根铁棒竖直插入圆柱体容器中,甲棒露在容器外面,乙棒露在容器外面,则甲、乙两根铁棒的长度之比为( )。
A.3:5 B.5:6 C.9:10 D.9:15
三、计算题(24分)
18.化简比(6分)
0.375: :2 3时45分:50分钟
19.脱式计算(能简算用简算)(9分)
45×+43× (-+)÷ 2024×
20.解方程(9分)
:x= x:0.25 = 13:(x+5)=
四、操作题(3+3=6分)
涂一涂,使涂色部分和未涂色部分方格数的比是5:3,并说一说你是怎样理解“涂色部分和未涂色部分方格数的比是5:3”的。
我的想法:
五、解决问题(6+6+7+7+8=34分)
21.聪聪打算自制蜂蜜水,他往15克的蜂蜜原料中加入60克水后,发现一份调制说明书(如下图)。请帮聪聪判断:为了使口感最佳,应往已调制的蜂蜜水中加水还是加蜂蜜原料?应加多少克?
22.白棋子比黑棋子多18枚,将黑白棋子各加上1枚后,黑棋子正好是白棋子的比是1:3。现在黑白棋子共有多少枚?
23.聪聪读一本书,第一天读了全书的,第二天再读了18页,这时已读与未读的页数之比是3:2。这本书共有多少页?
24.水果店共运进 114 筐水果,香蕉筐数的、梨的筐数的与苹果筐数的相等.这三种水果各有多少筐
25.如图所示,在直角三角形ABC的三边长度分别是6cm、8cm、10cm,把直角三角形ABC的∠B沿AE对折,使B与F点重合在线段AC上,这个三角形中阴影部分的面积是多少立方厘米?
参考答案
(第4单元)
一、填空题(第1题4分,其余每题2分,共26分)
1. (3)÷4==( 21 ):28=0.75=
解析:此题考查除法、分数、小数与比的转化关系。抓住已知数0.75入手即可。
2.若a÷b=0.625,则b:a=( 5 ):( 8 ),b比a多。
解析:此题考查分数与比转化关系。0.625==5:8;(8-5)÷5=
3.一辆汽车从甲地开往乙地,小时行驶了80千米,这辆汽车行驶的路程与时间比值是(),这个比值表示的意义是(这辆汽车的速度)。
解析:此题考查比值的求解方法和实际意义。80÷=
4.甲、乙、丙三个数的平均数是150,甲、乙、丙三数的比是4:5:6,乙数是( 150 )。
解析:此题考查比的应用,和比问题。
三个数的和是150×3=450,按比分配,乙数=450×=150
5.甲、乙两列火车的速度比是5:6,甲车行驶的路时间比乙车少,那么这两列火车行驶的路程( 5 ):( 18 )。
解析:此题考查复比问题,分数与比的转化关系。
速度比=5:6
时间比=(1-):1=1:3
路程比=(5×1):(6×3)=5:18
6.甲、乙两辆汽车同时从A、B两地出发,相向而行,6小时相遇,甲车再行4小时即可到达B地。那么乙车再行( 9 )小时到达A地。
解析:此题考查比的应用。
甲行驶4小时的路程相当于乙行驶6小时的路程。在里程相同的情况下,甲乙所用时间的比是4:6=(4+6):(6+9)
7.如图所示,一个底面是正方形的长方体,其侧面积是1200平方厘米,底面边长与高之比是1:3。那么这个长方体的体积是( 3000 )立方厘米。
解析:比的应用
侧面积中一个面的面积是1200÷4=300(平方厘米)=10×30
因为长与高是1:3=10:30
所以底面边长为10厘米,高为30厘米,体积为10×10×30=3000立方厘米。
8.如图所示,大小正方形中阴影部分的面积比是3:2,那么大小正方形中空白部分的面积比是( 3 ):( 1 )。
解析:甲与乙两个三角形是属于等高模型,底之比就是三角形面积之比。所以大小正方形边长之比为3:2,面积之比为32:22=9:4.
所以空白部分面积之比为:(9-3):(4-2)=3:1
9.如图所示,由4个完全相同的小长方形拼成一个大长方形,已知大长方形的周长是56dm,则每个 小长方形的面积是( 48 )dm2。
解析:通过我观察,很容易发现大长方形的长与宽的比是(3+1):3=4:3
长=56÷2×=16(厘米)
宽=56÷2-16=12(厘米)
小长方形面积=16×12÷4=48(cm2)
10.一个等腰三角形中两条边的长度之比为1:2,这两条边的长度相差2cm,这个等腰三角形的周长是( 10 )cm。
解析:考查比的应用和三角形三边关系两个知识点。
等腰三角形三边之比为1:1:2(1+1=2),不符合任意两边之和大于第三边三角形三边关系,不符合题意,舍去;应该为1:2:2、
得出等腰三角形周长=2÷(2-1)×(1+2+2)=10(cm)
11.今年王老师与聪聪的年龄比是7:3,再过5年,王老师与聪聪的年龄比2:1,今年王老师与聪聪的年龄分别是( 35 )、( 15 )岁。
解析:考查抓住不变量(年龄差不变)转化单位“1”问题。
解法一:
今年王老师的年龄相当于王老师与聪聪年龄差的,5年之后,王老师的年龄相当于王老师与聪聪年龄差的。
王老师与聪聪年龄差=5÷(-)=20(岁)
王老师年龄=20×=35(岁)
聪聪年龄=20×=15(岁)或35-20=15(岁)
解法二:
解:设王老师今年的年龄为x岁,则聪聪的年龄为x岁。
X+5=2(x+5)
X=35
聪聪x=×35=15(岁)
12. 一个分数的分子和分母的和是18,如果将分子加上8,分母加上9,新的分数约分后是,那么原来的分数是( )。
解析:分子与分母的和比问题。
(1)分子与分母的和是18+8+9=35;分子与分母之比为3:4.
(2)新分数的分子是35×=15,分母是35×=20,即现在的分数是
(3)15-8=7,20-9=11,所以,原来的分数是
二、选择题(10分)
13.甲与乙的比是4:5那些说法正确的是( C )。
A. 甲比乙少 B.乙比甲多 C.甲占甲、乙之和的 D.乙占甲、乙之和的
解析:考查比与分数关系转化
14.被减数、减数与差三数之和是32,减数与差的比是5:3,这差是( A )。
A.6 B.12 C.32
解析:考查减数与差的和倍问题:32÷2÷(5+3)×3=6
15.在正方形ABCD中,已知BE:EC=1:2,三角形DEC的面积占总面积的( A )。
A. B. C. D.
解析:采用分割法即可解答。
16.小明花了40元买了2本笔记本和4支钢笔,笔记本和钢笔的单价比是1:2,笔记本和钢笔的单价分别是( C )。
A.1元和2元 B.2元和4元 C.4元和8元 D.8元和10元。
解析:复比问题
笔记本和钢笔数量比2:4,单价比1:2,总价比(2×1):(4×2)=1:4。
笔记本总价=40÷(1+4)×1=8(元),单价8÷2=4(元)
钢笔单价=4×2=8(元)
17.甲、乙两根铁棒竖直插入圆柱体容器中,甲棒露在容器外面,乙棒露在容器外面,则甲、乙两根铁棒的长度之比为( C )。
A.3:5 B.5:6 C.9:10 D.9:15
解析:等式换比。甲棒和乙棒在容器里面部分长度相等。
即甲棒×(1-)=乙棒×(1-),设甲棒×=乙棒×=1
甲棒:乙棒=:=9:10
三、计算题(24分)
18.化简比(6分)
0.375: :2 3时45分:50分钟
=: =: =225分钟:50分钟
=25:32 =20:77 =9:2
19.脱式计算(能简算用简算)(9分)
45×+43× (-+)÷ 2024×
=(44+1)×+(44-1)× =(-+)×60 =(2023+)×
=44×(+)+- =45-24+10 =2022+1
=28.5 =31 =2023
20.解方程(9分)
:x= x:0.25 = 13:(x+5)=
解:x=÷ 解:x=0.25× 解:
X= x=
X=
四、操作题(3+3=6分)
涂一涂,使涂色部分和未涂色部分方格数的比是5:3,并说一说你是怎样理解“涂色部分和未涂色部分方格数的比是5:3”的。
我的想法:
我的想法:把方格总数平均分成8份,每份是3格,涂色部分占5份就是15格,未涂色部分占3份就是9格。(言之有理即可)
五、解决问题(6+6+7+7+8=34分)
21.聪聪打算自制蜂蜜水,他往15克的蜂蜜原料中加入60克水后,发现一份调制说明书(如下图)。请帮聪聪判断:为了使口感最佳,应往已调制的蜂蜜水中加水还是加蜂蜜原料?应加多少克?
解答:15:60=,>,15÷-60=40(g)
答:应往已调制的蜂蜜水中加水,应加40g。
22.白棋子比黑棋子多18枚,将黑白棋子各加上1枚后,黑棋子正好是白棋子的比是1:3。现在黑白棋子共有多少枚?
解析:差比问题。
差不变:将黑白棋子各加上1枚后,白棋子比黑棋子还是多18枚,且黑棋子正好是白棋子的比是1:3。
现在黑棋子=18÷(3-1)×1=9(枚)
现在白棋子=18÷(3-1)×3=27(枚)
现在一共9+27=36(枚)
答:(略)
23.聪聪读一本书,第一天读了全书的,第二天再读了18页,这时已读与未读的页数之比是3:2。这本书共有多少页?
解析:转化单位“1”。
把“这时已读与未读的页数之比是3:2”转化为“已读的页数占全书页数的”
根据量率对应关系:18页占全书的-。
列式:18÷(-)=80(页)
答:(略)
24.水果店共运进 114 筐水果,香蕉筐数的、梨的筐数的与苹果筐数的相等.这三种水果各有多少筐
解析:考查等式换比。
设:香蕉筐数×=梨的筐数×=苹果筐数×=1
所以香蕉:梨:苹果=(1÷):(1÷):(1÷)=6:8:5
114÷(6+8+5)=6(筐)
香蕉:6×6=36(筐)
梨:6×8=48(筐)
苹果:6×5=30(筐)
答:(略)
25.如图所示,在直角三角形ABC的三边长度分别是6cm、8cm、10cm,把直角三角形ABC的∠B沿AE对折,使B与F点重合在线段AC上,这个三角形中阴影部分的面积是多少立方厘米?
解析:
方法一:底高模型。
在△AEC中,△AEF和△FEC构成等高模型。两个三角形的面积之比就是底之比。
所以S△AEF:S△FEC=6:(10-6)=3:2;又因为△AEF和△AEB为重叠三角形,所以此两个三角形面积相等。所以S△AEB:S△AEF:S△FEC=3:3:2。所以阴影△EFC面积为△ABC面积的:
列式:6×8÷2×=6(cm2)
方法二:方程法
解:设BE=x,则EF=x.
根据关系式:S△ABE+S△AEC=S△ABC
得出方程:6x÷2+10x÷2=6×8÷2
3x+5x=24
X=3
所以S△EFC=(10-6)×3÷2=6(cm2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
