北师大版八年级上学期第一次月考数学试题(含解析)
文档属性
| 名称 | 北师大版八年级上学期第一次月考数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 372.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 08:40:38 | ||
图片预览




文档简介
北师大版八年级上学期第一次月考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.实数9的算术平方根是( )
A.3 B. C. D.
2.计算的结果是( )
A. B.1 C. D.3
3.下列二次根式中,不能与合并的是( )
A. B. C. D.
4.实数﹣2023的绝对值是( )
A.2023 B.﹣2023 C. D.
5.如图是由一串有公共点O的直角三角形演化而成的,,那么的长为( )
A. B.4 C.3 D.
6.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
A.6000米 B.5000米 C.4000米 D.2000米
7.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别为4,6,3,4,则最大正方形E的面积是( )
A.17 B.34 C.77 D.86
8.已知一个直角三角形的两边长分别为6和8,则第三边长的平方是( )
A.100 B.28 C.10或14 D.100或28
9.估计的值应在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
10.实数在数轴上的对应点的位置如图所示,若,则A,B,C,D四个点中可能是原点的为( )
A.A点 B.B点 C.C点 D.D点
二、填空题
11.要使代数式有意义,则x可以取的最小整数是 .
12.已知x,y都是实数,且,则 .
13.对于任意两个不相等的实数,定义一种新运算“”如下:,如:.那么 .
14.已知跷跷板长为3.9米,小明和小红坐在两端玩跷跷板,在这个过程中,跷跷板的两端端点在水平方向的距离的最小值为3.6米,此时较高端点距离地面的高度等于 米.
15.一个正数a的两个平方根是和,则的立方根为 .
三、解答题
16.计算:①×﹣5
②
③
④(+)2
17.已知实数的平方根是,的立方根是,求式子的值.
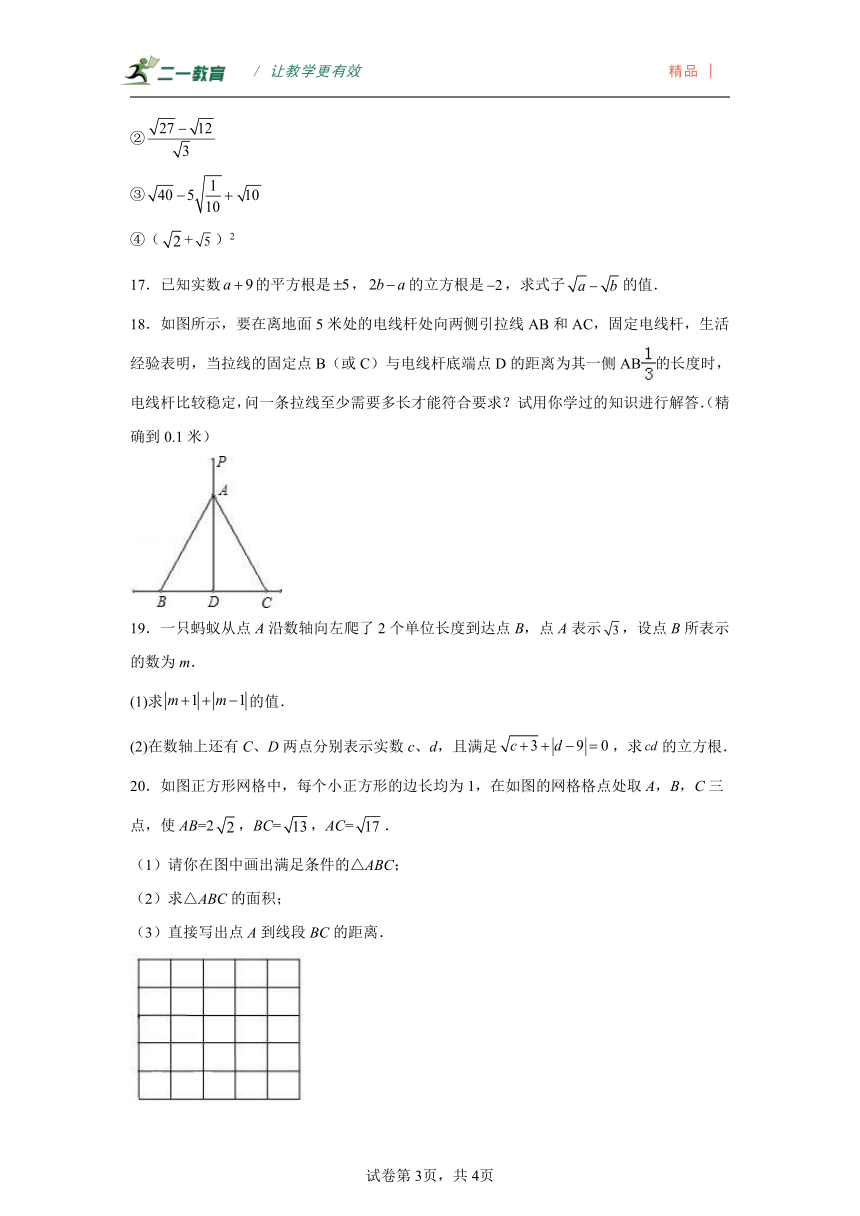
18.如图所示,要在离地面5米处的电线杆处向两侧引拉线AB和AC,固定电线杆,生活经验表明,当拉线的固定点B(或C)与电线杆底端点D的距离为其一侧AB的长度时,电线杆比较稳定,问一条拉线至少需要多长才能符合要求?试用你学过的知识进行解答.(精确到0.1米)
19.一只蚂蚁从点A沿数轴向左爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)求的值.
(2)在数轴上还有C、D两点分别表示实数c、d,且满足,求的立方根.
20.如图正方形网格中,每个小正方形的边长均为1,在如图的网格格点处取A,B,C三点,使AB=2,BC=,AC=.
(1)请你在图中画出满足条件的△ABC;
(2)求△ABC的面积;
(3)直接写出点A到线段BC的距离.
21.)若a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是=-1,-1的差倒数是.已知a1=-,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推.
(1)分别求出a2,a3,a4的值;
(2)求a1+a2+a3+…+a2160的值.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据算术平方根的定义即可求出结果.
【详解】解:,
故选:A.
【点睛】本题考查了平方根和算术平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
2.B
【分析】把括号内的每一项分别乘以 再合并即可.
【详解】解:
故选:B.
【点睛】本题考查的是二次根式的乘法运算,掌握“二次根式的乘法运算法则”是解本题的关键.
3.C
【分析】化简二次根式,根据最简二次根式的被开方数相同,可得答案.
【详解】解:A、,能与合并,故A不符合题意;
B、,能与合并,故B不符合题意;
C、,不能与合并,故C符合题意;
D、,能与合并,故D不符合题意.
故选:C.
【点睛】本题主要考查了同类二次根式, 关键是掌握被开方数相同的最简二次根式是同类二次根式.
4.A
【分析】根据绝对值的代数意义即可得出答案.
【详解】解:因为负数的绝对值等于它的相反数,
所以,﹣2023的绝对值等于2023.
故选:A.
【点睛】本题考查了绝对值的代数意义,熟练掌握知识点是本题的关键.
5.D
【分析】根据勾股定理可以求得OA2,OA3,OA4,OA5的值,即可发现数值的变化特点,从而可以求得OA8的长.
【详解】解:由图可得,
…,
,
故选:D.
【点睛】本题考查勾股定理、数字类规律探索,解答本题的关键是发现数字的变化特点,利用勾股定理与二次根式的化简解答是关键.
6.B
【详解】【分析】连接AC,由勾股定理可得AC=.
【详解】连接AC
由已知可得∠ABC=90°
所以,由勾股定理可得AC=米,
所以, 张明家与王强家的距离为5000米.
故选B
【点睛】本题考核知识点:勾股定理. 解题关键点:构造直角三角形.
7.C
【分析】根据正方形的面积公式,结合勾股定理,能够导出正方形A,B,C,D的面积和即为最大正方形的面积.
【详解】解:如下图:
根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,
S1=42+62,S2=32+42,
于是S3=S1+S2,
即可得S3=16+36+9+16=77.
故选:C.
【点睛】本题考查了勾股定理的知识,根据勾股定理的几何意义表示出S3是解答本题的关键.
8.D
【分析】根据已知条题意,求第三边的长必须分类讨论,即8是斜边或是直角边的两种情况,然后利用勾股定理即可求解.
【详解】解: 当8是直角边时,设第三边为斜边值x,
由勾股定理得:,
当8是斜边时,则可设第三边直角边值y,
由勾股定理得:.
故答案为:D.
【点睛】本题考查了勾股定理解直角三角形,当已知条件没有明确哪边是斜边时,必须分类讨论.
9.B
【分析】根据利用夹逼法得到取值范围,即可得到答案;
【详解】解:由题意可得,
,
∵,
∴,
∴,
故选B.
【点睛】本题考查根数的估算,解题的关键是将原来的根数变形.
10.D
【分析】分①若原点的位置为A点时,②若原点的位置为B点或C点时,③若原点的位置为D点时,结合有理数的加法法则和点在数轴上的位置分析即可得出正确选项.
【详解】解:根据数轴可知,
①若原点的位置为A点时,x>0,则,,,
∴,舍去;
②若原点的位置为B点或C点时,,
则或,,
∴,舍去;
③若原点的位置为D点时,
则 ,
∴,符合条件,
∴最有可能是原点的是D点,
故选:D.
【点睛】本题考查实数与数轴,有理数的加法法则,化简绝对值.熟记有理数的加法法则是解题关键.
11.3
【分析】
本题主要考查了二次根式有意义的条件.根据“二次根式的被开方数为非负数”,即可求解.
【详解】解:根据题意得:,
解得:,
∴x可以取的最小整数是3.
故答案为:3
12.4
【分析】利用二次根式被开方数的非负性求出x值,再代入求出y值,即可求解.
【详解】解:∵,
∴,,
∴,
将代入,
得:,
故答案为:4.
【点睛】本题考查了二次根式被开方数的非负性,熟练掌握并灵活运用二次根式被开方数的非负性是解题的关键.
13.
【分析】根据新定义,将,代入计算即可.
【详解】解:∵,
∴,
故答案为:.
【点睛】本题考查实数的计算,解题的关键是将,正确代入再化简.
14./
【分析】设较高端点距离地面的高度为h米,此时,跷跷板长即为直角三角形的斜边长,两端端点在水平方向的距离的最小值即为一条直角边长,利用勾股定理即可求出结果.
【详解】解:设较高端点距离地面的高度为h米,
根据勾股定理得:h2=3.92﹣3.62=2.25,
∴h=1.5(米),
故答案为:1.5.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解决问题的关键.
15.2
【分析】根据一个正数的平方根互为相反数,将和相加等于0,列出方程,解出b,再将b代入任意一个平方根中,进行平方运算求出这个正数a,将算出后,求立方根即可.
【详解】∵和是正数a的平方根,
∴,
解得 ,
将b代入,
∴正数 ,
∴,
∴的立方根为:,
故填:2.
【点睛】本题考查正数的平方根的性质,求一个数的立方根,解题关键是知道一个正数的两个平方根互为相反数.
16.①1;②1;③④
【分析】①根据二次根式的乘法计算即可;
②根据二次根式的加减法则和乘除法则计算即可;
③化简二次根式,根据二次根式的加减法则计算即可;
④根据二次根式的运算法则计算即可
【详解】①原式=
②原式=
③原式=
④原式=
【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的混合运算是解题的关键.
17.
【分析】此题考查了立方根以及平方根,利用平方根,立方根定义求出a与b的值,代入原式计算即可求出值.
【详解】解:根据题意得:,
解得:,
则原式
18.5.3米
【详解】试题分析:根据题意得出BD与AB的长度关系,然后在Rt△ADB中利用勾股定理的应用进行解答即可.
解:如图,BD=AB,AD=5,
在Rt△ADB中,AD2+BD2=AB2
即52+(AB)2=AB2,
∴AB=≈5.3.
答:一条拉线至少需5.3米长才能符合要求.
【点评】本题考查勾股定理的运用,属于理论结合实际的题目,解答关键把实际问题转化为数学问题加以计算.
19.(1)2
(2)
【分析】(1)根据点的移动先表示,再代入代数式化简绝对值即可;
(2)根据非负数的性质可得,,再代入代数式计算即可;
【详解】(1)解:由题意可知
∴
.
(2)∵,,,
∴,,
∴,
∴的立方根为.
【点睛】本题考查的是实数的绝对值的化简,算术平方根的非负性的应用,求解一个数的立方根,掌握以上基础知识是解本题的关键.
20.(1)画图见解析;(2)5;(3).
【分析】(1)在正方形网格中,根据勾股定理画出线段AB,BC,AC,从而画出△ABC;
(2)利用分割法求三角形的面积即可;
(3)利用三角形的面积公式,可求点B到线段AC的距离.
【详解】解:(1)△ABC如图所示:
(2)S△ABC=3×4-×2×2-×2×3-×4×1=5.
(3)作AH⊥BC于H.
∵S△ABC= BC AH=5,
∴AH=,
∴点A到线段BC的距离为.
【点睛】本题考查了勾股定理,三角形的面积等知识,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方.
21.(1),4,-,(2)3180.
【详解】试题分析:(1)根据差倒数的定义进行计算即可得解;
(2)根据计算可知,每三个数为一个循环组循环,求出每一个循环组的三个数的和,再用2160除以3求出正好有720个循环组,然后求解即可.
试题解析:(1)∵a1=-,
∴a2=,
a3=,
a4=;
(2)根据(1)可知,每三个数为一个循环组循环,
∵a1+a2+a3=-++4=,2160÷3=720,
∴a1+a2+a3+…+a2160=×720=3180.
考点:规律型:数字的变化类.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.实数9的算术平方根是( )
A.3 B. C. D.
2.计算的结果是( )
A. B.1 C. D.3
3.下列二次根式中,不能与合并的是( )
A. B. C. D.
4.实数﹣2023的绝对值是( )
A.2023 B.﹣2023 C. D.
5.如图是由一串有公共点O的直角三角形演化而成的,,那么的长为( )
A. B.4 C.3 D.
6.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
A.6000米 B.5000米 C.4000米 D.2000米
7.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别为4,6,3,4,则最大正方形E的面积是( )
A.17 B.34 C.77 D.86
8.已知一个直角三角形的两边长分别为6和8,则第三边长的平方是( )
A.100 B.28 C.10或14 D.100或28
9.估计的值应在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
10.实数在数轴上的对应点的位置如图所示,若,则A,B,C,D四个点中可能是原点的为( )
A.A点 B.B点 C.C点 D.D点
二、填空题
11.要使代数式有意义,则x可以取的最小整数是 .
12.已知x,y都是实数,且,则 .
13.对于任意两个不相等的实数,定义一种新运算“”如下:,如:.那么 .
14.已知跷跷板长为3.9米,小明和小红坐在两端玩跷跷板,在这个过程中,跷跷板的两端端点在水平方向的距离的最小值为3.6米,此时较高端点距离地面的高度等于 米.
15.一个正数a的两个平方根是和,则的立方根为 .
三、解答题
16.计算:①×﹣5
②
③
④(+)2
17.已知实数的平方根是,的立方根是,求式子的值.
18.如图所示,要在离地面5米处的电线杆处向两侧引拉线AB和AC,固定电线杆,生活经验表明,当拉线的固定点B(或C)与电线杆底端点D的距离为其一侧AB的长度时,电线杆比较稳定,问一条拉线至少需要多长才能符合要求?试用你学过的知识进行解答.(精确到0.1米)
19.一只蚂蚁从点A沿数轴向左爬了2个单位长度到达点B,点A表示,设点B所表示的数为m.
(1)求的值.
(2)在数轴上还有C、D两点分别表示实数c、d,且满足,求的立方根.
20.如图正方形网格中,每个小正方形的边长均为1,在如图的网格格点处取A,B,C三点,使AB=2,BC=,AC=.
(1)请你在图中画出满足条件的△ABC;
(2)求△ABC的面积;
(3)直接写出点A到线段BC的距离.
21.)若a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是=-1,-1的差倒数是.已知a1=-,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推.
(1)分别求出a2,a3,a4的值;
(2)求a1+a2+a3+…+a2160的值.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】根据算术平方根的定义即可求出结果.
【详解】解:,
故选:A.
【点睛】本题考查了平方根和算术平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
2.B
【分析】把括号内的每一项分别乘以 再合并即可.
【详解】解:
故选:B.
【点睛】本题考查的是二次根式的乘法运算,掌握“二次根式的乘法运算法则”是解本题的关键.
3.C
【分析】化简二次根式,根据最简二次根式的被开方数相同,可得答案.
【详解】解:A、,能与合并,故A不符合题意;
B、,能与合并,故B不符合题意;
C、,不能与合并,故C符合题意;
D、,能与合并,故D不符合题意.
故选:C.
【点睛】本题主要考查了同类二次根式, 关键是掌握被开方数相同的最简二次根式是同类二次根式.
4.A
【分析】根据绝对值的代数意义即可得出答案.
【详解】解:因为负数的绝对值等于它的相反数,
所以,﹣2023的绝对值等于2023.
故选:A.
【点睛】本题考查了绝对值的代数意义,熟练掌握知识点是本题的关键.
5.D
【分析】根据勾股定理可以求得OA2,OA3,OA4,OA5的值,即可发现数值的变化特点,从而可以求得OA8的长.
【详解】解:由图可得,
…,
,
故选:D.
【点睛】本题考查勾股定理、数字类规律探索,解答本题的关键是发现数字的变化特点,利用勾股定理与二次根式的化简解答是关键.
6.B
【详解】【分析】连接AC,由勾股定理可得AC=.
【详解】连接AC
由已知可得∠ABC=90°
所以,由勾股定理可得AC=米,
所以, 张明家与王强家的距离为5000米.
故选B
【点睛】本题考核知识点:勾股定理. 解题关键点:构造直角三角形.
7.C
【分析】根据正方形的面积公式,结合勾股定理,能够导出正方形A,B,C,D的面积和即为最大正方形的面积.
【详解】解:如下图:
根据勾股定理的几何意义,可得A、B的面积和为S1,C、D的面积和为S2,
S1=42+62,S2=32+42,
于是S3=S1+S2,
即可得S3=16+36+9+16=77.
故选:C.
【点睛】本题考查了勾股定理的知识,根据勾股定理的几何意义表示出S3是解答本题的关键.
8.D
【分析】根据已知条题意,求第三边的长必须分类讨论,即8是斜边或是直角边的两种情况,然后利用勾股定理即可求解.
【详解】解: 当8是直角边时,设第三边为斜边值x,
由勾股定理得:,
当8是斜边时,则可设第三边直角边值y,
由勾股定理得:.
故答案为:D.
【点睛】本题考查了勾股定理解直角三角形,当已知条件没有明确哪边是斜边时,必须分类讨论.
9.B
【分析】根据利用夹逼法得到取值范围,即可得到答案;
【详解】解:由题意可得,
,
∵,
∴,
∴,
故选B.
【点睛】本题考查根数的估算,解题的关键是将原来的根数变形.
10.D
【分析】分①若原点的位置为A点时,②若原点的位置为B点或C点时,③若原点的位置为D点时,结合有理数的加法法则和点在数轴上的位置分析即可得出正确选项.
【详解】解:根据数轴可知,
①若原点的位置为A点时,x>0,则,,,
∴,舍去;
②若原点的位置为B点或C点时,,
则或,,
∴,舍去;
③若原点的位置为D点时,
则 ,
∴,符合条件,
∴最有可能是原点的是D点,
故选:D.
【点睛】本题考查实数与数轴,有理数的加法法则,化简绝对值.熟记有理数的加法法则是解题关键.
11.3
【分析】
本题主要考查了二次根式有意义的条件.根据“二次根式的被开方数为非负数”,即可求解.
【详解】解:根据题意得:,
解得:,
∴x可以取的最小整数是3.
故答案为:3
12.4
【分析】利用二次根式被开方数的非负性求出x值,再代入求出y值,即可求解.
【详解】解:∵,
∴,,
∴,
将代入,
得:,
故答案为:4.
【点睛】本题考查了二次根式被开方数的非负性,熟练掌握并灵活运用二次根式被开方数的非负性是解题的关键.
13.
【分析】根据新定义,将,代入计算即可.
【详解】解:∵,
∴,
故答案为:.
【点睛】本题考查实数的计算,解题的关键是将,正确代入再化简.
14./
【分析】设较高端点距离地面的高度为h米,此时,跷跷板长即为直角三角形的斜边长,两端端点在水平方向的距离的最小值即为一条直角边长,利用勾股定理即可求出结果.
【详解】解:设较高端点距离地面的高度为h米,
根据勾股定理得:h2=3.92﹣3.62=2.25,
∴h=1.5(米),
故答案为:1.5.
【点睛】本题考查了勾股定理的应用,掌握勾股定理是解决问题的关键.
15.2
【分析】根据一个正数的平方根互为相反数,将和相加等于0,列出方程,解出b,再将b代入任意一个平方根中,进行平方运算求出这个正数a,将算出后,求立方根即可.
【详解】∵和是正数a的平方根,
∴,
解得 ,
将b代入,
∴正数 ,
∴,
∴的立方根为:,
故填:2.
【点睛】本题考查正数的平方根的性质,求一个数的立方根,解题关键是知道一个正数的两个平方根互为相反数.
16.①1;②1;③④
【分析】①根据二次根式的乘法计算即可;
②根据二次根式的加减法则和乘除法则计算即可;
③化简二次根式,根据二次根式的加减法则计算即可;
④根据二次根式的运算法则计算即可
【详解】①原式=
②原式=
③原式=
④原式=
【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的混合运算是解题的关键.
17.
【分析】此题考查了立方根以及平方根,利用平方根,立方根定义求出a与b的值,代入原式计算即可求出值.
【详解】解:根据题意得:,
解得:,
则原式
18.5.3米
【详解】试题分析:根据题意得出BD与AB的长度关系,然后在Rt△ADB中利用勾股定理的应用进行解答即可.
解:如图,BD=AB,AD=5,
在Rt△ADB中,AD2+BD2=AB2
即52+(AB)2=AB2,
∴AB=≈5.3.
答:一条拉线至少需5.3米长才能符合要求.
【点评】本题考查勾股定理的运用,属于理论结合实际的题目,解答关键把实际问题转化为数学问题加以计算.
19.(1)2
(2)
【分析】(1)根据点的移动先表示,再代入代数式化简绝对值即可;
(2)根据非负数的性质可得,,再代入代数式计算即可;
【详解】(1)解:由题意可知
∴
.
(2)∵,,,
∴,,
∴,
∴的立方根为.
【点睛】本题考查的是实数的绝对值的化简,算术平方根的非负性的应用,求解一个数的立方根,掌握以上基础知识是解本题的关键.
20.(1)画图见解析;(2)5;(3).
【分析】(1)在正方形网格中,根据勾股定理画出线段AB,BC,AC,从而画出△ABC;
(2)利用分割法求三角形的面积即可;
(3)利用三角形的面积公式,可求点B到线段AC的距离.
【详解】解:(1)△ABC如图所示:
(2)S△ABC=3×4-×2×2-×2×3-×4×1=5.
(3)作AH⊥BC于H.
∵S△ABC= BC AH=5,
∴AH=,
∴点A到线段BC的距离为.
【点睛】本题考查了勾股定理,三角形的面积等知识,关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方.
21.(1),4,-,(2)3180.
【详解】试题分析:(1)根据差倒数的定义进行计算即可得解;
(2)根据计算可知,每三个数为一个循环组循环,求出每一个循环组的三个数的和,再用2160除以3求出正好有720个循环组,然后求解即可.
试题解析:(1)∵a1=-,
∴a2=,
a3=,
a4=;
(2)根据(1)可知,每三个数为一个循环组循环,
∵a1+a2+a3=-++4=,2160÷3=720,
∴a1+a2+a3+…+a2160=×720=3180.
考点:规律型:数字的变化类.
答案第1页,共2页
答案第1页,共2页
同课章节目录
