12.3角的平分线的性质同步练习(含解析)
文档属性
| 名称 | 12.3角的平分线的性质同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 08:50:32 | ||
图片预览



文档简介
12.3 角的平分线的性质 同步练习
一、单选题
1.如图,点P是内一点,于C,于D,且,点E在上,,,则的度数是( )
A. B. C. D.
2.如图,的三边AC、BC、AB的长分别是8、12、16,点O是三条角平分线的交点,则的值为( )
A. B. C. D.
3.如图,△ABC中,AB=5,AC=7,BC=10.∠BAC的平分线AD交BC于点D.则DC的长度为 ( )
A. B.6 C. D.
4.如图,已知直角中,I为各内角平分线的交点,过I点作的垂线,垂足为H,若,,,那么的值为( )
A.2 B.3 C.4 D.5
5.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC的面积是△PBD面积的2倍,其中结论正确的个数有( )
A.4个 B.3个 C.2个 D.1个
6.如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
7.如图,已知在四边形中,,平分,,,,则四边形的面积是( )
A.24 B.30 C.36 D.42
8.如图,已知的周长是,点为与的平分线的交点,且于点,若,则的面积是( )
A. B. C. D.
二、填空题
9.如图,点为上任意一点,且于点,于点,,若,则 .
10.如图.在中,是边上的高,的角平分线交于,当,的面积为12时,的长为 .
11.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,△ABC的面积是 .
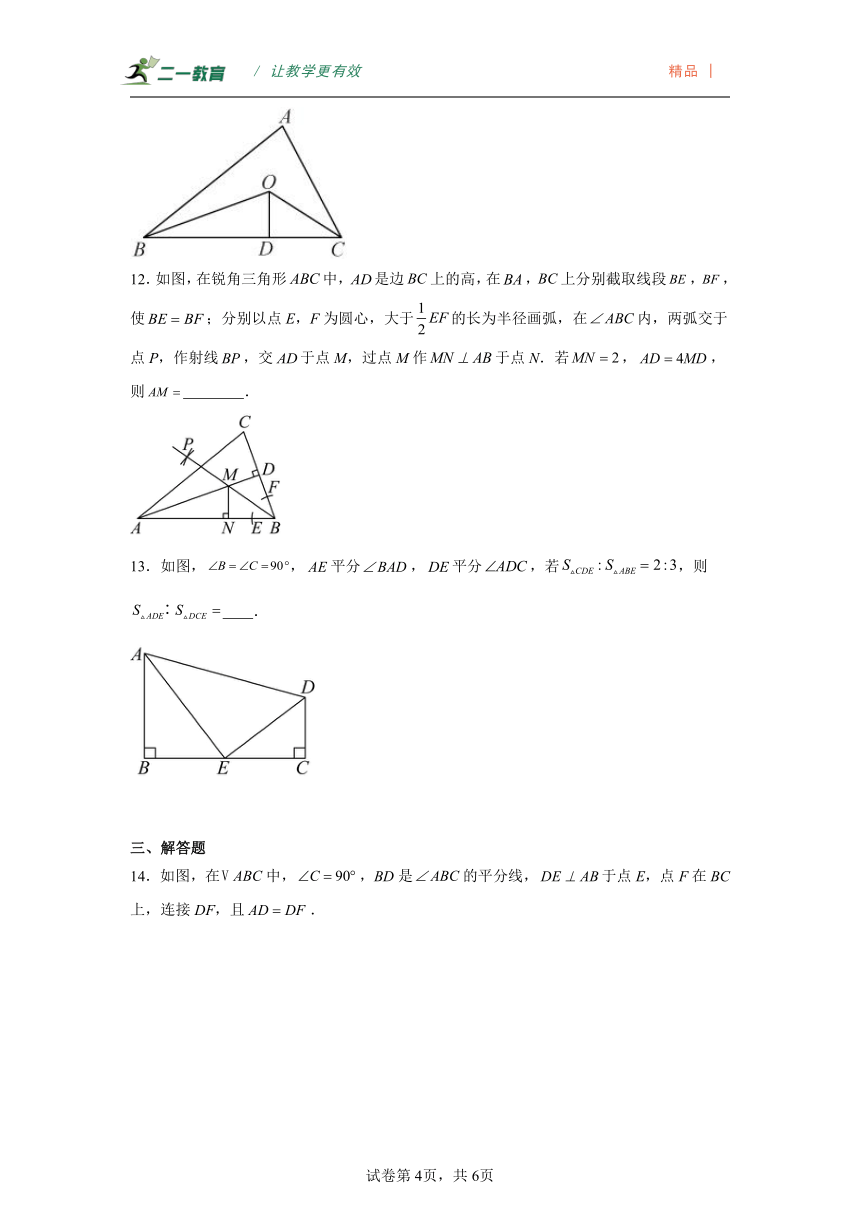
12.如图,在锐角三角形中,是边上的高,在,上分别截取线段,,使;分别以点E,F为圆心,大于的长为半径画弧,在内,两弧交于点P,作射线,交于点M,过点M作于点N.若,,则 .
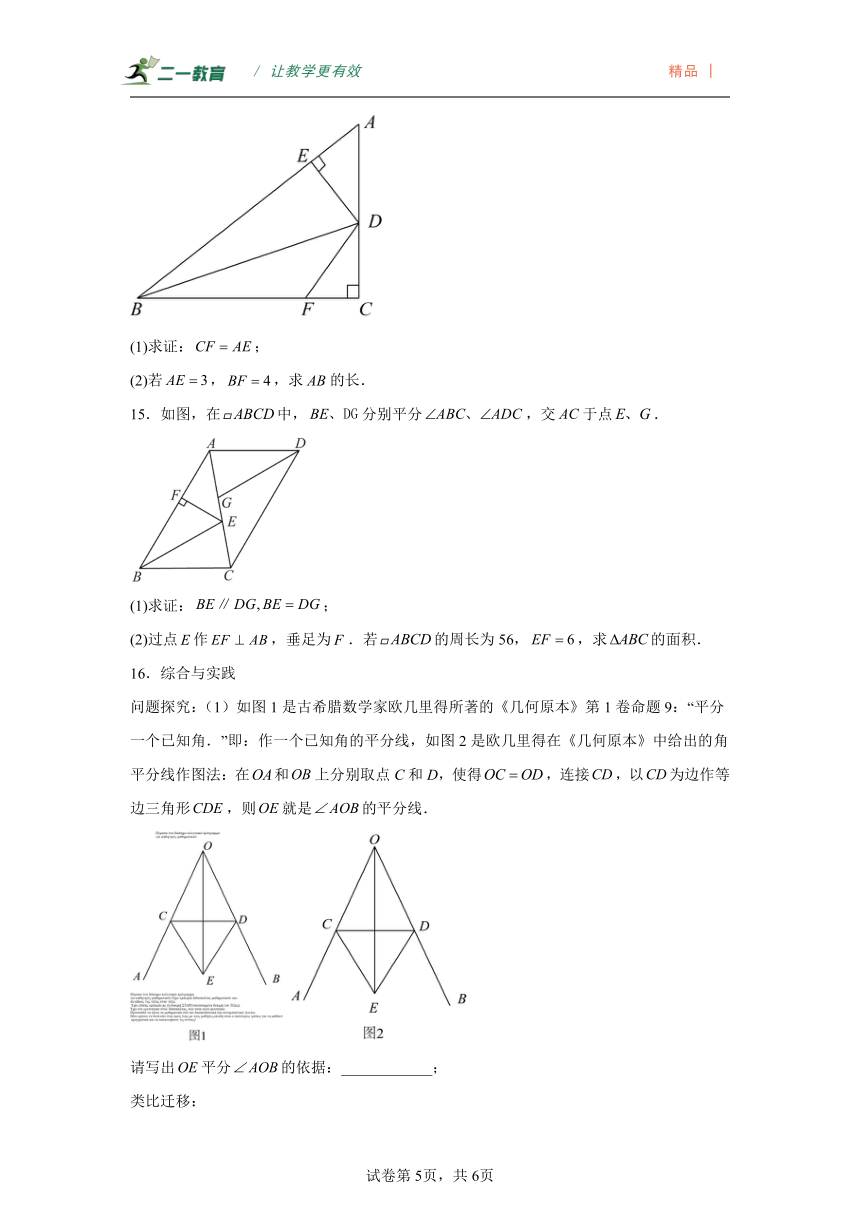
13.如图,,平分,平分,若,则 .
三、解答题
14.如图,在中,,BD是的平分线,于点E,点F在BC上,连接DF,且.
(1)求证:;
(2)若,,求AB的长.
15.如图,在中,分别平分,交于点.
(1)求证:;
(2)过点作,垂足为.若的周长为56,,求的面积.
16.综合与实践
问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得,连接,以为边作等边三角形,则就是的平分线.
请写出平分的依据:____________;
类比迁移:
(2)小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边,上分别取,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
拓展实践:
(3)小明将研究应用于实践.如图4,校园的两条小路和,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
17.(1)模型:如图1,在中,平分,,,求证:.
(2)模型应用:如图2,平分交的延长线于点,求证:.
(3)类比应用:如图3,平分,,,求证:.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据到角两边距离相等的点在角平分线上,从而求出,再利用外交与内角的关系求出结果.
【详解】,,,
平分,
,
又,
故选B.
【点睛】本题考查了角平分线的判定和与三角形有关的角的计算,解决问题的关键是角平分线的判定,然后利用角平分线的性质求出角,从而求解.
2.A
【分析】
过点O作于点D,于点E,于点F,根据角平分线的性质定理可知.再由三角形的面积公式计算,作比即可.
【详解】
如图,过点O作于点D,于点E,于点F,
∵点是三条角平分线的交点,
∴.
∵,
,
,
∴.
故选A.
【点睛】
本题主要考查角平分线的性质定理.正确作出辅助线,由角平分线的性质定理得出是解题关键.
3.A
【分析】作DE⊥AB于E,DF⊥AC于F,由角平分线性质得DE=DF,则△ABD与△ACD分别以AB、AC为底时高相等,则△ABD与△ACD的面积比=AB:AC=5:7;同时△ABD与△ACD分别以BD、DC为底时高也相等,则△ABD与△ACD的面积比=BD:DC=5:7;求解即可.
【详解】作DE⊥AB于E,DF⊥AC于F,
AD是∠BAC的平分线,
DE=DF,
AB=5,AC=7,
,
BC=10,
,
故选:A.
【点睛】本题考查了角平分线的性质定理及三角形的面积,熟练掌握知识点并能够准确作出辅助线是解题的关键.
4.A
【分析】作于,于,连接,根据角平分线的性质得到,根据三角形的面积公式计算即可得到答案.
【详解】作于,于,连接,如图:
为各内角平分线的交点,,,
,
则:
解得:,
故选:A.
【点睛】本题主要考查角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
5.A
【分析】过点P作PK⊥AB,垂足为点K.证明Rt△BPK≌Rt△BPD,△PAK≌△PCD,利用全等三角形的性质即可解决问题.
【详解】解:过点P作PK⊥AB,垂足为点K.
∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,
∴PK=PD,
在Rt△BPK和Rt△BPD中,
,
∴Rt△BPK≌Rt△BPD(HL),
∴BK=BD,
∵∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,
∴∠KPD=∠APC,
∴∠APK=∠CPD,故①正确,
在△PAK和△PCD中,
,
∴△PAK≌△PCD(ASA),
∴AK=CD,PA=PC,故②正确,
∴BK﹣AB=BC﹣BD,
∴BD﹣AB=BC﹣BD,
∴AB+BC=2BD,故③正确,
∵Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),
∴S△BPK=S△BPD,S△APK=S△PDC,
∴S四边形ABCP=S四边形KBDP=2S△PBD.故④正确.
故选A.
【点睛】本题考查全等三角形的判定和性质,角平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
6.A
【分析】过点D作DG⊥AB于点G,由角平分线的定义及平行线的性质可得∠ADB=90°,然后可证△ADC≌△ADB,△DEC≌△DFB,进而问题可求解.
【详解】解:∵AD平分∠BAC,BC平分∠ABF,
∴,
∵BF∥AC,
∴,
∴,即,
∴,即AD是△ABC的高,故①正确;
∵,AD=AD,
∴△ADC≌△ADB(ASA),
∴,即AD是△ABC的中线,故②正确;
∵BF∥AC,
∴,
∵,
∴△DEC≌△DFB(AAS),
∴ED=FD,故③正确;
过点D作DG⊥AB于点G,如图所示:
∵AD平分∠BAC,BC平分∠ABF,,
∴,
∵AD=AD,
∴(HL),
∴,
同理可知,
∵,
∴,故④正确;
综上所述:正确的个数有4个;
故选A.
【点睛】本题主要考查全等三角形的性质与判定、平行线的性质及角平分线的性质,熟练掌握全等三角形的性质与判定、平行线的性质及角平分线的性质是解题的关键.
7.B
【分析】过D作DE⊥AB交BA的延长线于E,根据角平分线的性质得到DE=CD=4,根据三角形的面积公式即可得到结论.
【详解】如图,过D作DE⊥AB交BA的延长线于E,
∵BD平分∠ABC,∠BCD=90°,
∴DE=CD=4,
∴四边形的面积
故选B.
【点睛】本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.
8.B
【分析】本题考查的是角平分线的性质:角的平分线上的点到角的两边的距离相等.作于E,于F,连接,根据角平分线的性质得到,根据三角形的面积公式计算即可.
【详解】解:作于E,于F,连接,
∵O为与的平分线的交点,,
∴,
∴的面积的面积的面积的面积
,
故选:B.
9.
【分析】根据角平分线的判定定理解答即可.
【详解】∵于点,于点,,
∴是的平分线,
∴,
故答案为:.
【点睛】本题考查的是角平分线的判定,掌握到角的两边的距离相等的点在角的平分线上是解题的关键.
10.3
【分析】本题主要考查了角平分线的性质,三角形面积计算,如图所示,过点E作于F,根据角平分线上的点到角两边的距离相等得到,再利用面积法求出的长即可得到答案.
【详解】解:如图所示,过点E作于F,
∵是边上的高,
∴,
∵的角平分线交于,,,
∴,
∵,的面积为12,
∴,
∴,
故答案为:3.
11.42
【分析】根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等(即OE=OD=OF),从而可得到的面积等于周长的一半乘以2,代入求出即可.
【详解】如下图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=4,
∵的周长是21,OD⊥BC于D,且OD=4,
∴
=42,
故答案为:42.
【点睛】本题主要考查了角平分线的性质及三角形面积的求法,熟练掌握角平分线的性质是解决本题的关键.
12.6
【分析】本题考查了尺规作图,角平分线的性质等知识,根据作图可知平分,根据角平分线的性质可知,结合求出,.
【详解】解:作图可知平分,
∵是边上的高,,,
∴,
∵,
∴,
∴,
故答案为:6.
13.
【分析】过点作于,根据角平分线上的点到角的两边距离相等可得,然后证明,根据全等三角形的面积相等可得,同理可得:,设,,表示出,然后求解即可.
【详解】如图,过点作于,
∵,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
同理:,
设,,
∴,
∴,
故答案为:.
【点睛】此题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.
14.(1)证明见解析
(2)10
【分析】(1)由角平分线的性质可得,证明,进而结论得证;
(2)证明,可得,根据计算求解即可.
【详解】(1)证明:(1)∵,
∴,
又∵BD是的平分线,,
∴,,
在和中,
∵,
∴,
∴.
(2)解:由(1)可得,
∴,
∵,
∴,
∴,
∵BD是的平分线,
∴,
在和中,
∵,
∴,
∴,
∴,
∴AB的长为10.
【点睛】本题考查了角平分线的性质,三角形全等的判定与性质.解题的关键在于熟练掌握角平分线的性质并证明三角形全等.
15.(1)见详解
(2)84
【分析】(1)由平行四边形的性质证即可求证;
(2)作,由即可求解;
【详解】(1)证明:在中,
∵,
∴,
∵分别平分,,
∴,
在和中,
∵
∴,
∴,
∴.
(2)如图,作,
∵的周长为56,
∴,
∵平分,
∴,
∴.
【点睛】本题主要考查平行四边形的性质、三角形的全等、角平分线的性质,掌握相关知识并灵活应用是解题的关键.
16.(1);(2)证明见解析;(3)作图见解析;
【分析】(1)先证明,可得,从而可得答案;
(2)先证明,可得,可得是的角平分线;
(3)先作的角平分线,再在角平分线上截取即可.
【详解】解:(1)∵,,,
∴,
∴,
∴是的角平分线;
故答案为:
(2)∵,,,
∴,
∴,
∴是的角平分线;
(3)如图,点即为所求作的点;
.
【点睛】本题考查的是全等三角形的判定与性质,角平分线的定义与角平分线的性质,作已知角的角平分线,理解题意,熟练的作角的平分线是解本题的关键.
17.(1)证明见解析;(2)证明见解析;(3)证明见解析;
【分析】(1)由题意得DE=DF,,,即可得出:=AB:AC;
(2)在AB上取点E,使得AE=AC,根据题意可证△ACD≌△AED,从而可求出,,即可求解;
(3)延长BE至M,使EM=DC,连接AM,根据题意可证△ADC≌△AEM,故而得出AE为∠BAM的角平分线,即,即可得出答案;
【详解】解:(1)∵AD平分∠BAC,DE⊥AB,DE⊥AC,
∴DE=DF,
∵ ,,
∴:=AB:AC;
(2)如图,在AB上取点E,使得AE=AC,连接DE
又∵ AD平分∠CAE,
∴ ∠CAD=∠DAE,
在△ACD和△AED中,
,
∴△ACD≌△AED(SAS),
∴CD=DE且∠ADC=∠ADE,
∴ ,
∴ ,
∴AB:AC=BD:CD;
(3)如图延长BE至M,使EM=DC,连接AM,
∵ ∠D+∠AEB=180°,
又∵∠AEB+∠AEM=180°,
∴∠D=∠AEM,
在△ADC与△AEM中,
,
∴△ADC≌△AEM(SAS),
∴∠DAC=∠EAM=∠BAE,AC=AM,
∴AE为∠BAM的角平分线,
故 ,
∴BE:CD=AB:AC;
【点睛】本题考查了全等三角形的判定与性质、角平分线的性质、以及三角形的面积的应用,正确掌握知识点是解题的关键;
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,点P是内一点,于C,于D,且,点E在上,,,则的度数是( )
A. B. C. D.
2.如图,的三边AC、BC、AB的长分别是8、12、16,点O是三条角平分线的交点,则的值为( )
A. B. C. D.
3.如图,△ABC中,AB=5,AC=7,BC=10.∠BAC的平分线AD交BC于点D.则DC的长度为 ( )
A. B.6 C. D.
4.如图,已知直角中,I为各内角平分线的交点,过I点作的垂线,垂足为H,若,,,那么的值为( )
A.2 B.3 C.4 D.5
5.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC的面积是△PBD面积的2倍,其中结论正确的个数有( )
A.4个 B.3个 C.2个 D.1个
6.如图,AD平分∠BAC,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF.则下列结论中:①AD是△ABC的高;②AD是△ABC的中线;③ED=FD;④AB=AE+BF.其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
7.如图,已知在四边形中,,平分,,,,则四边形的面积是( )
A.24 B.30 C.36 D.42
8.如图,已知的周长是,点为与的平分线的交点,且于点,若,则的面积是( )
A. B. C. D.
二、填空题
9.如图,点为上任意一点,且于点,于点,,若,则 .
10.如图.在中,是边上的高,的角平分线交于,当,的面积为12时,的长为 .
11.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,△ABC的面积是 .
12.如图,在锐角三角形中,是边上的高,在,上分别截取线段,,使;分别以点E,F为圆心,大于的长为半径画弧,在内,两弧交于点P,作射线,交于点M,过点M作于点N.若,,则 .
13.如图,,平分,平分,若,则 .
三、解答题
14.如图,在中,,BD是的平分线,于点E,点F在BC上,连接DF,且.
(1)求证:;
(2)若,,求AB的长.
15.如图,在中,分别平分,交于点.
(1)求证:;
(2)过点作,垂足为.若的周长为56,,求的面积.
16.综合与实践
问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得,连接,以为边作等边三角形,则就是的平分线.
请写出平分的依据:____________;
类比迁移:
(2)小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边,上分别取,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
拓展实践:
(3)小明将研究应用于实践.如图4,校园的两条小路和,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
17.(1)模型:如图1,在中,平分,,,求证:.
(2)模型应用:如图2,平分交的延长线于点,求证:.
(3)类比应用:如图3,平分,,,求证:.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据到角两边距离相等的点在角平分线上,从而求出,再利用外交与内角的关系求出结果.
【详解】,,,
平分,
,
又,
故选B.
【点睛】本题考查了角平分线的判定和与三角形有关的角的计算,解决问题的关键是角平分线的判定,然后利用角平分线的性质求出角,从而求解.
2.A
【分析】
过点O作于点D,于点E,于点F,根据角平分线的性质定理可知.再由三角形的面积公式计算,作比即可.
【详解】
如图,过点O作于点D,于点E,于点F,
∵点是三条角平分线的交点,
∴.
∵,
,
,
∴.
故选A.
【点睛】
本题主要考查角平分线的性质定理.正确作出辅助线,由角平分线的性质定理得出是解题关键.
3.A
【分析】作DE⊥AB于E,DF⊥AC于F,由角平分线性质得DE=DF,则△ABD与△ACD分别以AB、AC为底时高相等,则△ABD与△ACD的面积比=AB:AC=5:7;同时△ABD与△ACD分别以BD、DC为底时高也相等,则△ABD与△ACD的面积比=BD:DC=5:7;求解即可.
【详解】作DE⊥AB于E,DF⊥AC于F,
AD是∠BAC的平分线,
DE=DF,
AB=5,AC=7,
,
BC=10,
,
故选:A.
【点睛】本题考查了角平分线的性质定理及三角形的面积,熟练掌握知识点并能够准确作出辅助线是解题的关键.
4.A
【分析】作于,于,连接,根据角平分线的性质得到,根据三角形的面积公式计算即可得到答案.
【详解】作于,于,连接,如图:
为各内角平分线的交点,,,
,
则:
解得:,
故选:A.
【点睛】本题主要考查角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
5.A
【分析】过点P作PK⊥AB,垂足为点K.证明Rt△BPK≌Rt△BPD,△PAK≌△PCD,利用全等三角形的性质即可解决问题.
【详解】解:过点P作PK⊥AB,垂足为点K.
∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,
∴PK=PD,
在Rt△BPK和Rt△BPD中,
,
∴Rt△BPK≌Rt△BPD(HL),
∴BK=BD,
∵∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,
∴∠KPD=∠APC,
∴∠APK=∠CPD,故①正确,
在△PAK和△PCD中,
,
∴△PAK≌△PCD(ASA),
∴AK=CD,PA=PC,故②正确,
∴BK﹣AB=BC﹣BD,
∴BD﹣AB=BC﹣BD,
∴AB+BC=2BD,故③正确,
∵Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),
∴S△BPK=S△BPD,S△APK=S△PDC,
∴S四边形ABCP=S四边形KBDP=2S△PBD.故④正确.
故选A.
【点睛】本题考查全等三角形的判定和性质,角平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
6.A
【分析】过点D作DG⊥AB于点G,由角平分线的定义及平行线的性质可得∠ADB=90°,然后可证△ADC≌△ADB,△DEC≌△DFB,进而问题可求解.
【详解】解:∵AD平分∠BAC,BC平分∠ABF,
∴,
∵BF∥AC,
∴,
∴,即,
∴,即AD是△ABC的高,故①正确;
∵,AD=AD,
∴△ADC≌△ADB(ASA),
∴,即AD是△ABC的中线,故②正确;
∵BF∥AC,
∴,
∵,
∴△DEC≌△DFB(AAS),
∴ED=FD,故③正确;
过点D作DG⊥AB于点G,如图所示:
∵AD平分∠BAC,BC平分∠ABF,,
∴,
∵AD=AD,
∴(HL),
∴,
同理可知,
∵,
∴,故④正确;
综上所述:正确的个数有4个;
故选A.
【点睛】本题主要考查全等三角形的性质与判定、平行线的性质及角平分线的性质,熟练掌握全等三角形的性质与判定、平行线的性质及角平分线的性质是解题的关键.
7.B
【分析】过D作DE⊥AB交BA的延长线于E,根据角平分线的性质得到DE=CD=4,根据三角形的面积公式即可得到结论.
【详解】如图,过D作DE⊥AB交BA的延长线于E,
∵BD平分∠ABC,∠BCD=90°,
∴DE=CD=4,
∴四边形的面积
故选B.
【点睛】本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.
8.B
【分析】本题考查的是角平分线的性质:角的平分线上的点到角的两边的距离相等.作于E,于F,连接,根据角平分线的性质得到,根据三角形的面积公式计算即可.
【详解】解:作于E,于F,连接,
∵O为与的平分线的交点,,
∴,
∴的面积的面积的面积的面积
,
故选:B.
9.
【分析】根据角平分线的判定定理解答即可.
【详解】∵于点,于点,,
∴是的平分线,
∴,
故答案为:.
【点睛】本题考查的是角平分线的判定,掌握到角的两边的距离相等的点在角的平分线上是解题的关键.
10.3
【分析】本题主要考查了角平分线的性质,三角形面积计算,如图所示,过点E作于F,根据角平分线上的点到角两边的距离相等得到,再利用面积法求出的长即可得到答案.
【详解】解:如图所示,过点E作于F,
∵是边上的高,
∴,
∵的角平分线交于,,,
∴,
∵,的面积为12,
∴,
∴,
故答案为:3.
11.42
【分析】根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等(即OE=OD=OF),从而可得到的面积等于周长的一半乘以2,代入求出即可.
【详解】如下图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=4,
∵的周长是21,OD⊥BC于D,且OD=4,
∴
=42,
故答案为:42.
【点睛】本题主要考查了角平分线的性质及三角形面积的求法,熟练掌握角平分线的性质是解决本题的关键.
12.6
【分析】本题考查了尺规作图,角平分线的性质等知识,根据作图可知平分,根据角平分线的性质可知,结合求出,.
【详解】解:作图可知平分,
∵是边上的高,,,
∴,
∵,
∴,
∴,
故答案为:6.
13.
【分析】过点作于,根据角平分线上的点到角的两边距离相等可得,然后证明,根据全等三角形的面积相等可得,同理可得:,设,,表示出,然后求解即可.
【详解】如图,过点作于,
∵,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
同理:,
设,,
∴,
∴,
故答案为:.
【点睛】此题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.
14.(1)证明见解析
(2)10
【分析】(1)由角平分线的性质可得,证明,进而结论得证;
(2)证明,可得,根据计算求解即可.
【详解】(1)证明:(1)∵,
∴,
又∵BD是的平分线,,
∴,,
在和中,
∵,
∴,
∴.
(2)解:由(1)可得,
∴,
∵,
∴,
∴,
∵BD是的平分线,
∴,
在和中,
∵,
∴,
∴,
∴,
∴AB的长为10.
【点睛】本题考查了角平分线的性质,三角形全等的判定与性质.解题的关键在于熟练掌握角平分线的性质并证明三角形全等.
15.(1)见详解
(2)84
【分析】(1)由平行四边形的性质证即可求证;
(2)作,由即可求解;
【详解】(1)证明:在中,
∵,
∴,
∵分别平分,,
∴,
在和中,
∵
∴,
∴,
∴.
(2)如图,作,
∵的周长为56,
∴,
∵平分,
∴,
∴.
【点睛】本题主要考查平行四边形的性质、三角形的全等、角平分线的性质,掌握相关知识并灵活应用是解题的关键.
16.(1);(2)证明见解析;(3)作图见解析;
【分析】(1)先证明,可得,从而可得答案;
(2)先证明,可得,可得是的角平分线;
(3)先作的角平分线,再在角平分线上截取即可.
【详解】解:(1)∵,,,
∴,
∴,
∴是的角平分线;
故答案为:
(2)∵,,,
∴,
∴,
∴是的角平分线;
(3)如图,点即为所求作的点;
.
【点睛】本题考查的是全等三角形的判定与性质,角平分线的定义与角平分线的性质,作已知角的角平分线,理解题意,熟练的作角的平分线是解本题的关键.
17.(1)证明见解析;(2)证明见解析;(3)证明见解析;
【分析】(1)由题意得DE=DF,,,即可得出:=AB:AC;
(2)在AB上取点E,使得AE=AC,根据题意可证△ACD≌△AED,从而可求出,,即可求解;
(3)延长BE至M,使EM=DC,连接AM,根据题意可证△ADC≌△AEM,故而得出AE为∠BAM的角平分线,即,即可得出答案;
【详解】解:(1)∵AD平分∠BAC,DE⊥AB,DE⊥AC,
∴DE=DF,
∵ ,,
∴:=AB:AC;
(2)如图,在AB上取点E,使得AE=AC,连接DE
又∵ AD平分∠CAE,
∴ ∠CAD=∠DAE,
在△ACD和△AED中,
,
∴△ACD≌△AED(SAS),
∴CD=DE且∠ADC=∠ADE,
∴ ,
∴ ,
∴AB:AC=BD:CD;
(3)如图延长BE至M,使EM=DC,连接AM,
∵ ∠D+∠AEB=180°,
又∵∠AEB+∠AEM=180°,
∴∠D=∠AEM,
在△ADC与△AEM中,
,
∴△ADC≌△AEM(SAS),
∴∠DAC=∠EAM=∠BAE,AC=AM,
∴AE为∠BAM的角平分线,
故 ,
∴BE:CD=AB:AC;
【点睛】本题考查了全等三角形的判定与性质、角平分线的性质、以及三角形的面积的应用,正确掌握知识点是解题的关键;
答案第1页,共2页
答案第1页,共2页
