12.2三角形全等的判定练习(含解析)
文档属性
| 名称 | 12.2三角形全等的判定练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 678.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览

文档简介
12.2 三角形全等的判定练习
2024-2025学年人教版数学八年级上学期
一、单选题
1.如图,在和中,,,添加一个条件后,仍然不能证明,这个条件可能是( )
A. B. C. D.
2.如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
3.如图,点在上,,,添加一个条件,不能证明的是( )
A. B. C. D.
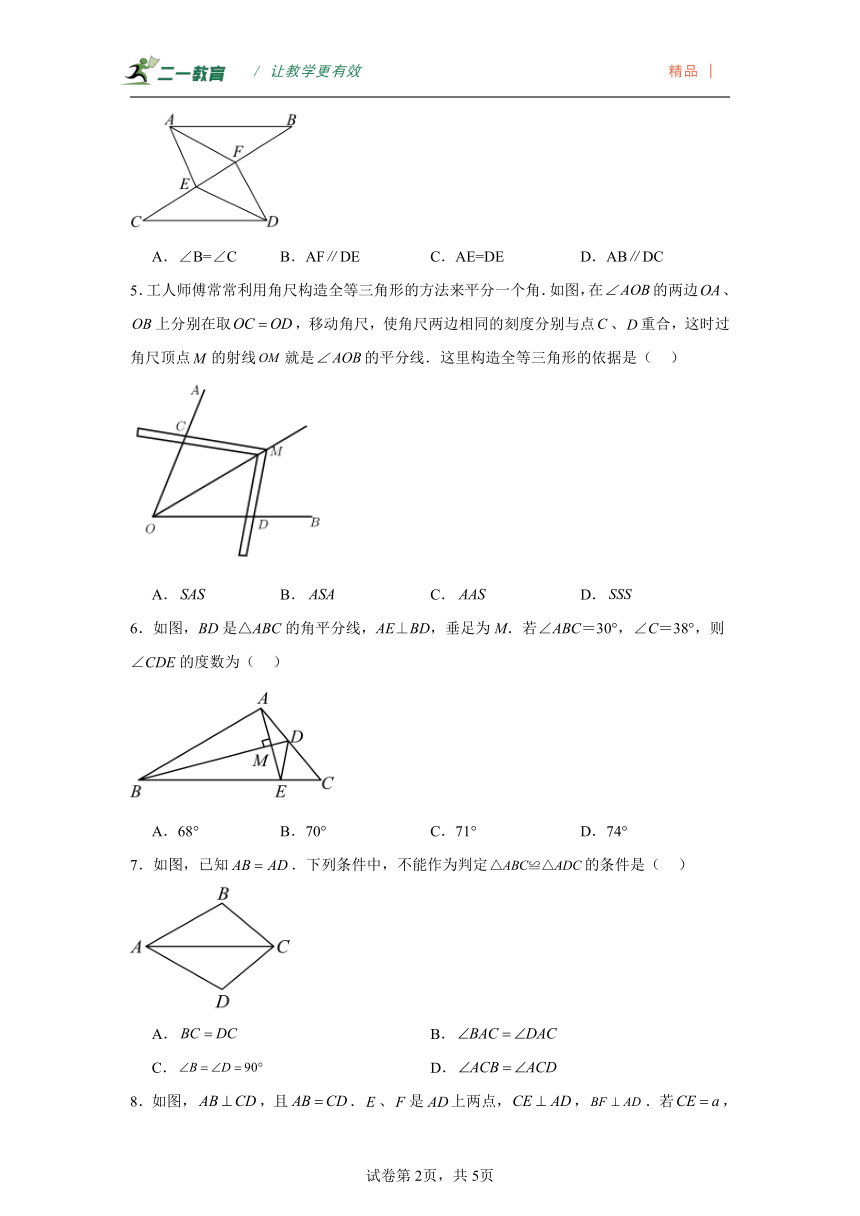
4.如图,E、F在线段BC上,AB=DC,AE=DF,BF=CE,下列问题不一定成立的是( )
A.∠B=∠C B.AF∥DE C.AE=DE D.AB∥DC
5.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取,移动角尺,使角尺两边相同的刻度分别与点、重合,这时过角尺顶点的射线就是的平分线.这里构造全等三角形的依据是( )
A. B. C. D.
6.如图,BD是△ABC的角平分线,AE⊥BD,垂足为M.若∠ABC=30°,∠C=38°,则∠CDE的度数为( )
A.68° B.70° C.71° D.74°
7.如图,已知.下列条件中,不能作为判定的条件是( )
A. B.
C. D.
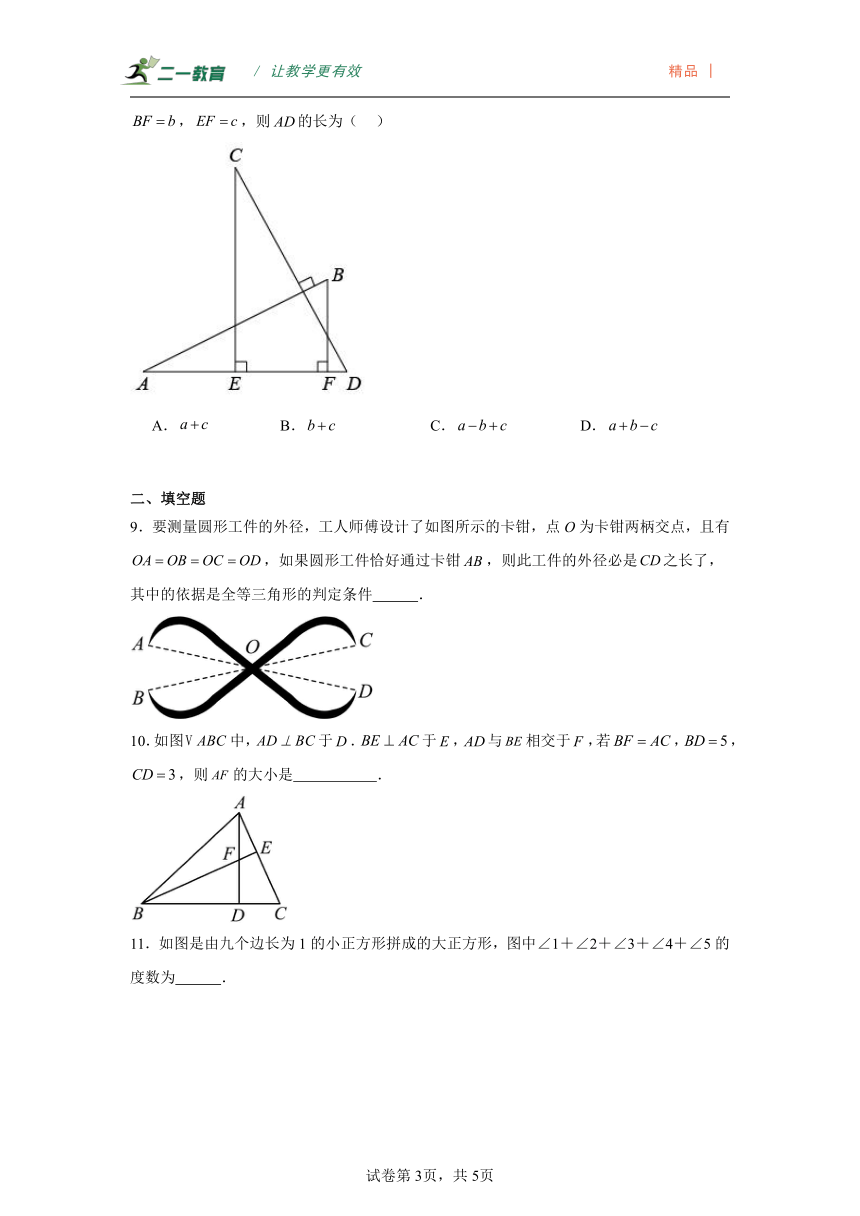
8.如图,,且.、是上两点,,.若,,,则的长为( )
A. B. C. D.
二、填空题
9.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有,如果圆形工件恰好通过卡钳,则此工件的外径必是之长了,其中的依据是全等三角形的判定条件 .
10.如图中,于.于,与相交于,若,,,则的大小是 .
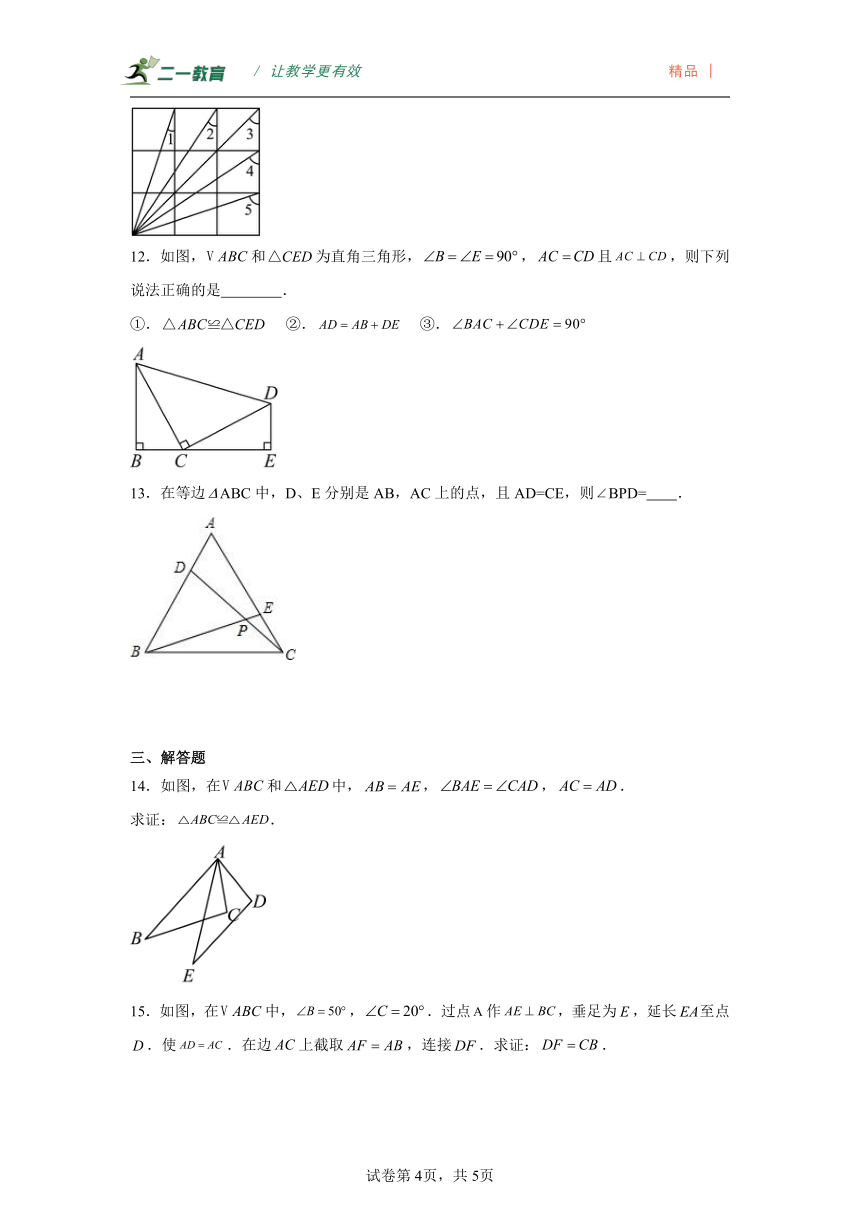
11.如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为 .
12.如图,和为直角三角形,,且,则下列说法正确的是 .
①. ②. ③.
13.在等边ABC中,D、E分别是AB,AC上的点,且AD=CE,则BPD= .
三、解答题
14.如图,在和中,,,.
求证:.
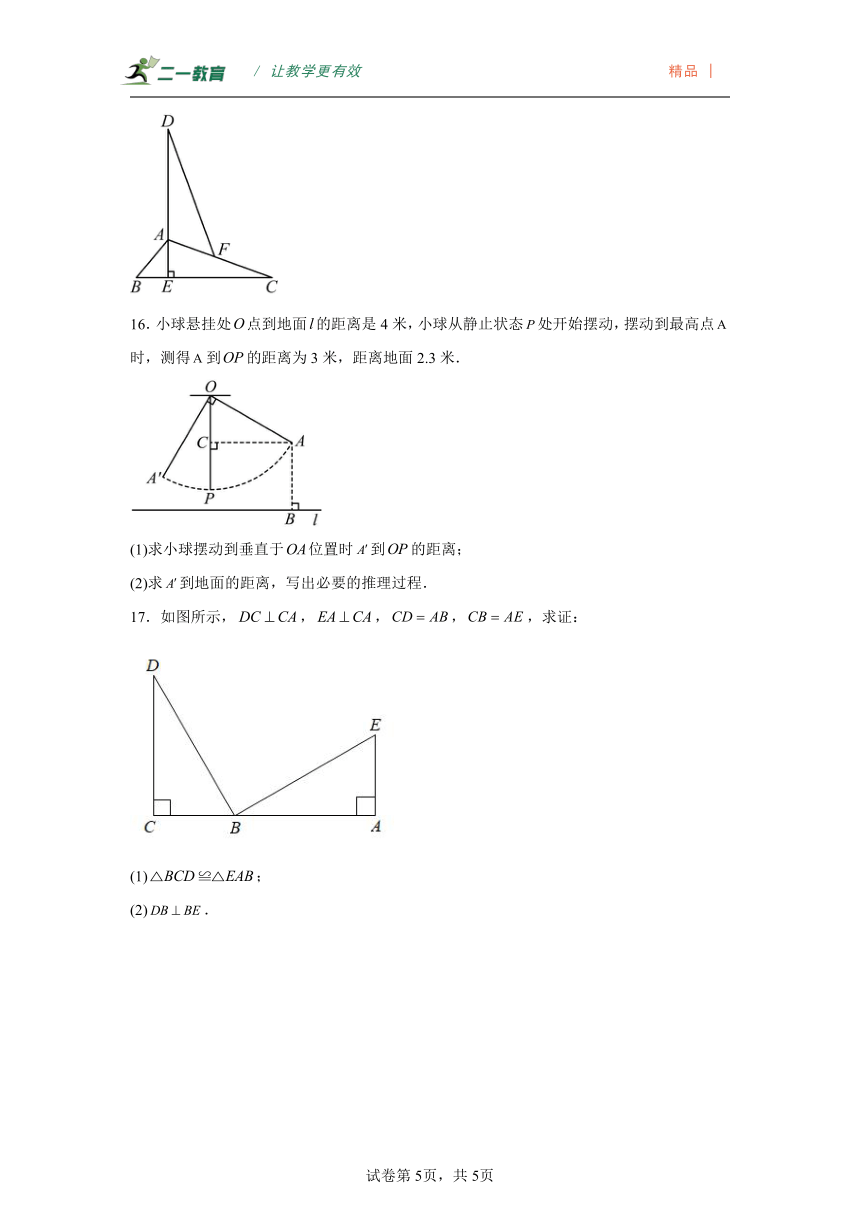
15.如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
16.小球悬挂处点到地面的距离是4米,小球从静止状态处开始摆动,摆动到最高点时,测得到的距离为3米,距离地面2.3米.
(1)求小球摆动到垂直于位置时到的距离;
(2)求到地面的距离,写出必要的推理过程.
17.如图所示,,,,,求证:
(1);
(2).
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据全等三角形的判定,利用、、即可得出答案.
【详解】解:∵,,
∴当时,由可得,故A不符合题意;
当时,则,由可得,故B不符合题意;
当时,则,由可得,故C不符合题意;
当时,不能得出,故D符合题意;
故选:D.
【点睛】本题主要考查全等三角形的判定,解答的关键是熟记全等三角形的判定条件并灵活运用.
2.A
【分析】根据全等三角形的SSS判定条件解答即可.
【详解】解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
3.D
【分析】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,全等三角形的判定定理有,两直角三角形全等还有等.根据求出,再根据全等三角形的判定定理进行分析即可.
【详解】解:∵,
∴,即,
,
∴当时,利用可得;
当时,利用可得;
当时,利用可得;
当时,无法证明;
故选:D.
4.C
【分析】先证明△ABE≌△DCF,然后证明出△ABF≌△CDE,再对选项进行一一分析即可.
【详解】∵BF=CE
∴BE=CF
在△ABE与△DCF中,有AB=DC,AE=DF,BE=CF
∴△ABE≌△DCF
∴∠B=∠C,故A正确
∴AB∥DC,故D正确
∴AB=CD
又∠B=∠C,BF=CE
∴△ABF≌△CDE
∴∠AFB=∠CED
∴AF∥DE,故B正确
无法证明AE=DE
故选C
【点睛】本题主要考查全等三角形的判定及性质,解题关键在于找到全等三角形.
5.D
【分析】根据全等三角形的判定条件判断即可.
【详解】解:由题意可知
在中
∴(SSS)
∴
∴就是的平分线
故选:D
【点睛】本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.
6.D
【分析】利用三角形内角和定理求出∠BAC=112°,利用全等三角形的性质证明∠BED=∠BAD即可解决问题.
【详解】解:∵∠ABC=30°,∠C=38°,
∴∠BAC=112°,
在△BMA和△BME中,
.
∴△BMA≌△BME(ASA),
∴BA=BE,
在△BDA和△BDE中,
,
∴△BDA≌△BDE(SAS),
∴∠BED=∠BAD=112°,
∴∠CED=68°,
∴∠CDE=180°-∠C-∠CED=74°,
故选:D.
【点睛】本题考查三角形内角和定理,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
7.D
【分析】本题考查了全等三角形的判定,根据全等三角形的判定方法逐一判断即可求解,掌握全等三角形的判定方法是解题的关键.
【详解】解:、,,,由可判断,该选项不合题意;
、,,,由可判断,该选项不合题意;
、,,,由可判断,该选项不合题意;
、,,不能判定,该选项符合题意;
故选:.
8.D
【详解】如图,
∵AB⊥CD,CE⊥AD,
∴∠1=∠2,
又∵∠3=∠4,
∴180°-∠1-∠4=180°-∠2-∠3,
即∠A=∠C.
∵BF⊥AD,
∴∠CED=∠BFD=90°,
∵AB=CD,
∴△ABF≌△CDE,
∴AF=CE=a,ED=BF=b,
又∵EF=c,
∴AD=a+b-c.
故选:D.
【点睛】本题主要考查全等三角形的判定与性质,证明△ABF≌△CDE是关键.
9.
【分析】本题考查了全等三角形的判定与性质,对顶角相等,即可作答.
【详解】解:连接,如图所示:
∵,
∴
故
故答案为:
10.2
【分析】根据三角形全等的判定和性质,先证,可得,即可解决问题;
【详解】解:于,于
,,
又(对顶角相等)
,
在和中,
,
,
,,
,
故答案为:2.
【点睛】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
11.225°
【分析】首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,即可求得∠1+∠2+∠3+∠4+∠5的值.
【详解】解:如图所示:
在△ABC和△AEF中,
∴△ABC≌△AEF(SAS),
∴∠5=∠BCA,
∴∠1+∠5=∠1+∠BCA=90°,
在Rt△ABD和Rt△AEH中,
∴Rt△ABD≌Rt△AEH(HL),
∴∠4=∠BDA,
∴∠2+∠4=∠2+∠BDA=90°,
∵∠3=45°,
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.
故答案为:225°.
【点睛】此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等即可求解.
12.①③/③①
【分析】先根据等角的余角相等可得,再结合已知条件可证,即可判定①;根据全等三角形的性质可得,,再根据线段的和差及等量代换可判定②,根据直角三角形两锐角互余以及等量代换可判定③;掌握全等三角形的判定与性质是解题的关键.
【详解】解:∵,,
∴,,
∴,
在和中,
,
∴,即①正确;
∴,
∴,即②错误;
∵,
∴,
∴,即③正确.
故答案为①③.
13.
【分析】根据SAS证出△CAD≌△BCE,得出∠DCA=∠EBC,再根据三角形的外角性质即可得出∠BPD的度数.
【详解】∵△ABC是等边三角形,
∴∠BAC=∠ACB,AC=BC,
在△CAD和△BCE中,,
∴△CAD≌△BCE(SAS),
∴∠DCA=∠EBC,
∴∠BPD=∠BCD+∠EBC =∠BCD+∠DCA =60°,
故答案为:60°.
【点睛】本题考查了三角形的判定与性质和三角形的外角性质,根据全等证出∠DCA=∠EBC是解决本题的关键.
14.见解析
【分析】本题考查了全等三角形的判定和性质,熟练掌握三角形全等的判定定理是解题关键.利用“”证明,即可解决问题.
【详解】证明:,
,即,
在和中,
,
.
15.见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点睛】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
16.(1)1.7米
(2)1米
【分析】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
(1)过作于点,证明,得到米,即可求解;
(2)由(1)得米,再求解即可.
【详解】(1)过作于点,
在和中,
米
(2)由(1)知:米
故到地面距离为:米.
17.(1)证明见解析;
(2)证明见解析.
【分析】(1)利用判定定理证明三角形全等即可;
(2)由,可得,,再利用,可得,即,
所以.
【详解】(1)证明:∵,,
∴,
在和中,
∴.
(2)证明:由(1)可知,
∴,,
∵,
∴,即,
∴.
【点睛】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.
答案第1页,共2页
答案第1页,共2页
2024-2025学年人教版数学八年级上学期
一、单选题
1.如图,在和中,,,添加一个条件后,仍然不能证明,这个条件可能是( )
A. B. C. D.
2.如图,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或② B.②或③ C.①或③ D.①或④
3.如图,点在上,,,添加一个条件,不能证明的是( )
A. B. C. D.
4.如图,E、F在线段BC上,AB=DC,AE=DF,BF=CE,下列问题不一定成立的是( )
A.∠B=∠C B.AF∥DE C.AE=DE D.AB∥DC
5.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取,移动角尺,使角尺两边相同的刻度分别与点、重合,这时过角尺顶点的射线就是的平分线.这里构造全等三角形的依据是( )
A. B. C. D.
6.如图,BD是△ABC的角平分线,AE⊥BD,垂足为M.若∠ABC=30°,∠C=38°,则∠CDE的度数为( )
A.68° B.70° C.71° D.74°
7.如图,已知.下列条件中,不能作为判定的条件是( )
A. B.
C. D.
8.如图,,且.、是上两点,,.若,,,则的长为( )
A. B. C. D.
二、填空题
9.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有,如果圆形工件恰好通过卡钳,则此工件的外径必是之长了,其中的依据是全等三角形的判定条件 .
10.如图中,于.于,与相交于,若,,,则的大小是 .
11.如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为 .
12.如图,和为直角三角形,,且,则下列说法正确的是 .
①. ②. ③.
13.在等边ABC中,D、E分别是AB,AC上的点,且AD=CE,则BPD= .
三、解答题
14.如图,在和中,,,.
求证:.
15.如图,在中,,.过点作,垂足为,延长至点.使.在边上截取,连接.求证:.
16.小球悬挂处点到地面的距离是4米,小球从静止状态处开始摆动,摆动到最高点时,测得到的距离为3米,距离地面2.3米.
(1)求小球摆动到垂直于位置时到的距离;
(2)求到地面的距离,写出必要的推理过程.
17.如图所示,,,,,求证:
(1);
(2).
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据全等三角形的判定,利用、、即可得出答案.
【详解】解:∵,,
∴当时,由可得,故A不符合题意;
当时,则,由可得,故B不符合题意;
当时,则,由可得,故C不符合题意;
当时,不能得出,故D符合题意;
故选:D.
【点睛】本题主要考查全等三角形的判定,解答的关键是熟记全等三角形的判定条件并灵活运用.
2.A
【分析】根据全等三角形的SSS判定条件解答即可.
【详解】解:∵AE=FB,
∴AE+BE=FB+BE,
∴AB=FE,
在△ABC和△FED中,
,
∴△ABC≌△FED(SSS),
∵AE=BE和BF=BE推不出AB=FE,
∴可利用的是①或②,
故选:A.
【点睛】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解答的关键.
3.D
【分析】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,全等三角形的判定定理有,两直角三角形全等还有等.根据求出,再根据全等三角形的判定定理进行分析即可.
【详解】解:∵,
∴,即,
,
∴当时,利用可得;
当时,利用可得;
当时,利用可得;
当时,无法证明;
故选:D.
4.C
【分析】先证明△ABE≌△DCF,然后证明出△ABF≌△CDE,再对选项进行一一分析即可.
【详解】∵BF=CE
∴BE=CF
在△ABE与△DCF中,有AB=DC,AE=DF,BE=CF
∴△ABE≌△DCF
∴∠B=∠C,故A正确
∴AB∥DC,故D正确
∴AB=CD
又∠B=∠C,BF=CE
∴△ABF≌△CDE
∴∠AFB=∠CED
∴AF∥DE,故B正确
无法证明AE=DE
故选C
【点睛】本题主要考查全等三角形的判定及性质,解题关键在于找到全等三角形.
5.D
【分析】根据全等三角形的判定条件判断即可.
【详解】解:由题意可知
在中
∴(SSS)
∴
∴就是的平分线
故选:D
【点睛】本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.
6.D
【分析】利用三角形内角和定理求出∠BAC=112°,利用全等三角形的性质证明∠BED=∠BAD即可解决问题.
【详解】解:∵∠ABC=30°,∠C=38°,
∴∠BAC=112°,
在△BMA和△BME中,
.
∴△BMA≌△BME(ASA),
∴BA=BE,
在△BDA和△BDE中,
,
∴△BDA≌△BDE(SAS),
∴∠BED=∠BAD=112°,
∴∠CED=68°,
∴∠CDE=180°-∠C-∠CED=74°,
故选:D.
【点睛】本题考查三角形内角和定理,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
7.D
【分析】本题考查了全等三角形的判定,根据全等三角形的判定方法逐一判断即可求解,掌握全等三角形的判定方法是解题的关键.
【详解】解:、,,,由可判断,该选项不合题意;
、,,,由可判断,该选项不合题意;
、,,,由可判断,该选项不合题意;
、,,不能判定,该选项符合题意;
故选:.
8.D
【详解】如图,
∵AB⊥CD,CE⊥AD,
∴∠1=∠2,
又∵∠3=∠4,
∴180°-∠1-∠4=180°-∠2-∠3,
即∠A=∠C.
∵BF⊥AD,
∴∠CED=∠BFD=90°,
∵AB=CD,
∴△ABF≌△CDE,
∴AF=CE=a,ED=BF=b,
又∵EF=c,
∴AD=a+b-c.
故选:D.
【点睛】本题主要考查全等三角形的判定与性质,证明△ABF≌△CDE是关键.
9.
【分析】本题考查了全等三角形的判定与性质,对顶角相等,即可作答.
【详解】解:连接,如图所示:
∵,
∴
故
故答案为:
10.2
【分析】根据三角形全等的判定和性质,先证,可得,即可解决问题;
【详解】解:于,于
,,
又(对顶角相等)
,
在和中,
,
,
,,
,
故答案为:2.
【点睛】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
11.225°
【分析】首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,即可求得∠1+∠2+∠3+∠4+∠5的值.
【详解】解:如图所示:
在△ABC和△AEF中,
∴△ABC≌△AEF(SAS),
∴∠5=∠BCA,
∴∠1+∠5=∠1+∠BCA=90°,
在Rt△ABD和Rt△AEH中,
∴Rt△ABD≌Rt△AEH(HL),
∴∠4=∠BDA,
∴∠2+∠4=∠2+∠BDA=90°,
∵∠3=45°,
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.
故答案为:225°.
【点睛】此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等即可求解.
12.①③/③①
【分析】先根据等角的余角相等可得,再结合已知条件可证,即可判定①;根据全等三角形的性质可得,,再根据线段的和差及等量代换可判定②,根据直角三角形两锐角互余以及等量代换可判定③;掌握全等三角形的判定与性质是解题的关键.
【详解】解:∵,,
∴,,
∴,
在和中,
,
∴,即①正确;
∴,
∴,即②错误;
∵,
∴,
∴,即③正确.
故答案为①③.
13.
【分析】根据SAS证出△CAD≌△BCE,得出∠DCA=∠EBC,再根据三角形的外角性质即可得出∠BPD的度数.
【详解】∵△ABC是等边三角形,
∴∠BAC=∠ACB,AC=BC,
在△CAD和△BCE中,,
∴△CAD≌△BCE(SAS),
∴∠DCA=∠EBC,
∴∠BPD=∠BCD+∠EBC =∠BCD+∠DCA =60°,
故答案为:60°.
【点睛】本题考查了三角形的判定与性质和三角形的外角性质,根据全等证出∠DCA=∠EBC是解决本题的关键.
14.见解析
【分析】本题考查了全等三角形的判定和性质,熟练掌握三角形全等的判定定理是解题关键.利用“”证明,即可解决问题.
【详解】证明:,
,即,
在和中,
,
.
15.见解析
【分析】利用三角形内角和定理得的度数,再根据全等三角形的判定与性质可得结论.
【详解】证明:在 中,,,
.
.
.
,
.
在和中,
,
∴.
.
【点睛】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
16.(1)1.7米
(2)1米
【分析】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
(1)过作于点,证明,得到米,即可求解;
(2)由(1)得米,再求解即可.
【详解】(1)过作于点,
在和中,
米
(2)由(1)知:米
故到地面距离为:米.
17.(1)证明见解析;
(2)证明见解析.
【分析】(1)利用判定定理证明三角形全等即可;
(2)由,可得,,再利用,可得,即,
所以.
【详解】(1)证明:∵,,
∴,
在和中,
∴.
(2)证明:由(1)可知,
∴,,
∵,
∴,即,
∴.
【点睛】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.
答案第1页,共2页
答案第1页,共2页
