2024-2025学年浙江省杭州市上城区绿城育华学校九年级(上)月考数学试卷(10月份)(含答案)
文档属性
| 名称 | 2024-2025学年浙江省杭州市上城区绿城育华学校九年级(上)月考数学试卷(10月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 10:46:47 | ||
图片预览




文档简介
2024-2025学年浙江省杭州市上城区绿城育华学校九年级(上)月考
数学试卷(10月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知的半径为,点到圆心的距离为,则点与的位置关系是( )
A. 点在外 B. 点在上 C. 点在内 D. 无法确定
2.盒子里有个球,它们只有颜色不同,其中红球有个,黄球有个,黑球有个小军从中任意摸一个球,下面说法正确的是( )
A. 一定是红球 B. 摸出红球的可能性最大
C. 不可能是黑球 D. 摸出黄球的可能性最小
3.如图是海上风力发电装置,相同的三个转子叶片呈均匀分布若图案绕中心旋转后能与原图案重合,则可以取( )
A.
B.
C.
D.
4.设的两条直角边长分别为,,则此直角三角形外接圆半径为( )
A. B. C. D. 或
5.关于二次函数的图象,下列说法正确的是( )
A. 对称轴是直线 B. 当时,随的增大而减小
C. 最小值是 D. 图象与轴没有交点
6.已知抛物线上的部分点的横坐标与纵坐标的对应值如表,则方程的根是( )
A. , B. , C. , D. ,
7.两名同学在研究函数为常数时,甲发现当时,是方程的一个根;乙发现时,该函数图象的对称轴在直线的右侧,则( )
A. 甲正确,乙正确 B. 甲正确,乙错误 C. 甲错误,乙正确 D. 甲错误,乙错误
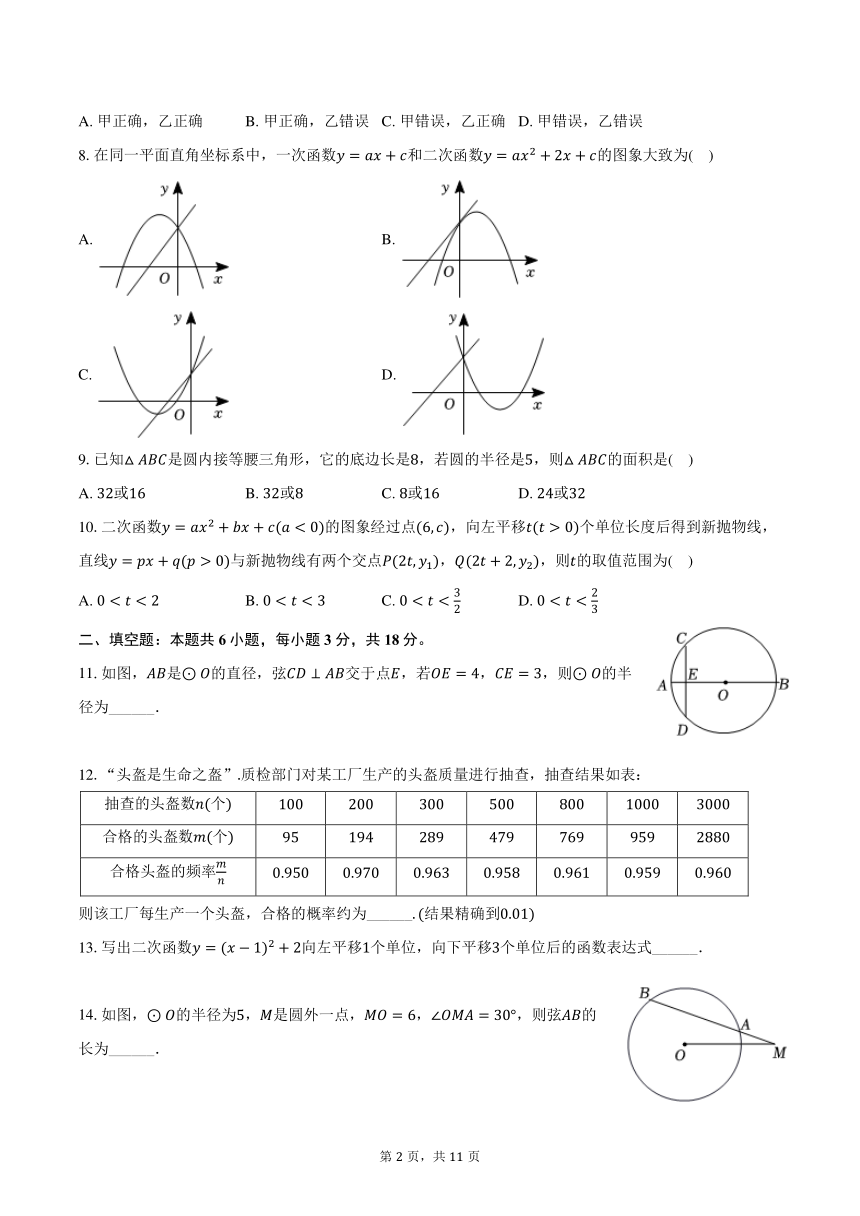
8.在同一平面直角坐标系中,一次函数和二次函数的图象大致为( )
A. B.
C. D.
9.已知是圆内接等腰三角形,它的底边长是,若圆的半径是,则的面积是( )
A. 或 B. 或 C. 或 D. 或
10.二次函数的图象经过点,向左平移个单位长度后得到新抛物线,直线与新抛物线有两个交点,,则的取值范围为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,是的直径,弦交于点,若,,则的半径为______.
12.“头盔是生命之盔”质检部门对某工厂生产的头盔质量进行抽查,抽查结果如表:
抽查的头盔数个
合格的头盔数个
合格头盔的频率
则该工厂每生产一个头盔,合格的概率约为______结果精确到
13.写出二次函数向左平移个单位,向下平移个单位后的函数表达式______.
14.如图,的半径为,是圆外一点,,,则弦的长为______.
15.若抛物线与轴有两个交点,则这两个交点间的距离称为该抛物线在轴上截得的“弦长”则下列抛物线:;;其中“弦长”最短的是抛物线______填题序号即可.
16.已知二次函数的图象经过点,,且满足当时,该函数的最大值为,最小值为, ______请用含的代数式表示.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知在平面直角坐标系中的位置如图所示.
画出绕点按顺时针方向旋转的;
在的条件下,仅使用无刻度的直尺作出的外接圆圆心,请在图中标出点的位置,要求保留作图痕迹,痕迹用实线表示不写作法,并直接写出圆心的坐标:______.
18.本小题分
在平面直角坐标系中,二次函数的图象与一次函数的图象交于点和点,点为二次函数图象的顶点.
求一次函数的表达式和点的坐标;
结合图象直接写出不等式的解集.
19.本小题分
有四张牌,点数分别是、、、,洗牌后把牌背面向上放好.
若增加张点数为偶数的牌,使得只抽一张抽到奇数和偶数的概率相等,直接填写的值: ______为正整数;
小丽先从这四张牌中抽一张,小芳从剩下的三张牌中抽一张,求两张牌上的数字之和是奇数的概率,请用列表或画树状图的方法说明.
20.本小题分
如图,等腰三角形内接于,,,点为的中点,连结.
求证:平分;
求的半径.
21.本小题分
如图,有两种尺寸的正方形,正方形的边长为,正方形的边长为,经过计算发现,,和的边长均不小于,使用个正方形和个正方形拼出如图所示的图案.
求的取值范围;
求图案中五个正方形的面积和的最大值.
22.本小题分
诗句“君到姑苏见,人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州.小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面宽度时,拱顶高出水平面,货船宽,船舱顶部为矩形并高出水面.
请你帮助小勇求此圆弧形拱桥的半径;
小勇在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
23.本小题分
如图,将球从点的正上方的点处发出,把球看成点,其运行的高度与运行的水平距离满足关系式.
若当小球运动的水平距离为时,小球达到最大高度,求小球达到的最大高度.
若小球的正前方处有一个截面为长方形的球筐,其中为,为,若要使小球落人筐中,求的取值范围.
24.本小题分
已知二次函数是实数.
求函数顶点坐标用含的代数式表示;
若,且函数顶点在轴上,当时,函数最大值为,求的值;
对于该二次函数图象上的两点,,当时,始终有成立求的取值范围.
参考答案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.
17.
18.解:抛物线的对称轴为:直线,
由题意得:,
解得:,
一次函数的表达式为:,
;
由图象得:不等式的解集为:.
19.
20.证明:如图,连接,,
是直径,
,
与都是直角三角形,
在与中,
,
≌,
,
平分;
解:如图,连接,设与交于点,
由可知,垂直平分,
,
在中,由勾股定理得,
,
设,则,
在中,由勾股定理得,
,
,
解得,
的半径为.
21.解:由题意可得,,,
,
,即,解得:,
;
根据题意有,
,
,即,
,
,
当时,,取得最大值,最大值为,
的最大值为.
22.解:如图,连接.
,
为中点,
,
,
又,
设,则.
在中,根据勾股定理得:,
解得.
答:此圆弧形拱桥的半径为.
此货船不能顺利通过这座拱桥,理由如下:
连接,
,船舱顶部为长方形并高出水面,
,
,
在中,由勾股定理得:,
.
此货船不能顺利通过这座拱桥.
23.解:小球运动的水平距离为时,小球达到最大高度,
抛物线的对称轴为:直线.
.
解得:.
由题意得:抛物线上点的坐标为.
.
抛物线的解析式为:.
当时,.
答:小球达到的最大高度为;
由题意得:点的坐标为,点的坐标为.
抛物线上点的坐标为,
.
抛物线的解析式为:.
抛物线经过点.
.
解得:.
抛物线经过点.
.
解得:.
要使小球落人筐中,的取值范围为:.
24.解:,
函数顶点坐标为;
函数顶点在轴上,
,
解得或,
,
,
二次函数解析式为,
对称轴为直线,
当时,即,此时在对称轴右侧,
,
当时,有最大值,即,
解得,舍去,
;
当时,在对称轴左侧,
,
当时,有最大值,即,
解得,舍去,
;
当时,此时有最大值,与题矛盾,故舍去;
综上所述,或;
由知二次函数图象的对称轴为,且开口向下,
二次函数图象上的两点,,时,始终有成立,
点到对称轴的距离小于或等于点到对称轴的距离,
,即,
,
即,
,
,
,
即,
,
解得:,
,
.
第1页,共1页
数学试卷(10月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知的半径为,点到圆心的距离为,则点与的位置关系是( )
A. 点在外 B. 点在上 C. 点在内 D. 无法确定
2.盒子里有个球,它们只有颜色不同,其中红球有个,黄球有个,黑球有个小军从中任意摸一个球,下面说法正确的是( )
A. 一定是红球 B. 摸出红球的可能性最大
C. 不可能是黑球 D. 摸出黄球的可能性最小
3.如图是海上风力发电装置,相同的三个转子叶片呈均匀分布若图案绕中心旋转后能与原图案重合,则可以取( )
A.
B.
C.
D.
4.设的两条直角边长分别为,,则此直角三角形外接圆半径为( )
A. B. C. D. 或
5.关于二次函数的图象,下列说法正确的是( )
A. 对称轴是直线 B. 当时,随的增大而减小
C. 最小值是 D. 图象与轴没有交点
6.已知抛物线上的部分点的横坐标与纵坐标的对应值如表,则方程的根是( )
A. , B. , C. , D. ,
7.两名同学在研究函数为常数时,甲发现当时,是方程的一个根;乙发现时,该函数图象的对称轴在直线的右侧,则( )
A. 甲正确,乙正确 B. 甲正确,乙错误 C. 甲错误,乙正确 D. 甲错误,乙错误
8.在同一平面直角坐标系中,一次函数和二次函数的图象大致为( )
A. B.
C. D.
9.已知是圆内接等腰三角形,它的底边长是,若圆的半径是,则的面积是( )
A. 或 B. 或 C. 或 D. 或
10.二次函数的图象经过点,向左平移个单位长度后得到新抛物线,直线与新抛物线有两个交点,,则的取值范围为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,是的直径,弦交于点,若,,则的半径为______.
12.“头盔是生命之盔”质检部门对某工厂生产的头盔质量进行抽查,抽查结果如表:
抽查的头盔数个
合格的头盔数个
合格头盔的频率
则该工厂每生产一个头盔,合格的概率约为______结果精确到
13.写出二次函数向左平移个单位,向下平移个单位后的函数表达式______.
14.如图,的半径为,是圆外一点,,,则弦的长为______.
15.若抛物线与轴有两个交点,则这两个交点间的距离称为该抛物线在轴上截得的“弦长”则下列抛物线:;;其中“弦长”最短的是抛物线______填题序号即可.
16.已知二次函数的图象经过点,,且满足当时,该函数的最大值为,最小值为, ______请用含的代数式表示.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知在平面直角坐标系中的位置如图所示.
画出绕点按顺时针方向旋转的;
在的条件下,仅使用无刻度的直尺作出的外接圆圆心,请在图中标出点的位置,要求保留作图痕迹,痕迹用实线表示不写作法,并直接写出圆心的坐标:______.
18.本小题分
在平面直角坐标系中,二次函数的图象与一次函数的图象交于点和点,点为二次函数图象的顶点.
求一次函数的表达式和点的坐标;
结合图象直接写出不等式的解集.
19.本小题分
有四张牌,点数分别是、、、,洗牌后把牌背面向上放好.
若增加张点数为偶数的牌,使得只抽一张抽到奇数和偶数的概率相等,直接填写的值: ______为正整数;
小丽先从这四张牌中抽一张,小芳从剩下的三张牌中抽一张,求两张牌上的数字之和是奇数的概率,请用列表或画树状图的方法说明.
20.本小题分
如图,等腰三角形内接于,,,点为的中点,连结.
求证:平分;
求的半径.
21.本小题分
如图,有两种尺寸的正方形,正方形的边长为,正方形的边长为,经过计算发现,,和的边长均不小于,使用个正方形和个正方形拼出如图所示的图案.
求的取值范围;
求图案中五个正方形的面积和的最大值.
22.本小题分
诗句“君到姑苏见,人家尽枕河”所描绘的就是有东方威尼斯之称的水城苏州.小勇要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面宽度时,拱顶高出水平面,货船宽,船舱顶部为矩形并高出水面.
请你帮助小勇求此圆弧形拱桥的半径;
小勇在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
23.本小题分
如图,将球从点的正上方的点处发出,把球看成点,其运行的高度与运行的水平距离满足关系式.
若当小球运动的水平距离为时,小球达到最大高度,求小球达到的最大高度.
若小球的正前方处有一个截面为长方形的球筐,其中为,为,若要使小球落人筐中,求的取值范围.
24.本小题分
已知二次函数是实数.
求函数顶点坐标用含的代数式表示;
若,且函数顶点在轴上,当时,函数最大值为,求的值;
对于该二次函数图象上的两点,,当时,始终有成立求的取值范围.
参考答案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.
13.
14.
15.
16.
17.
18.解:抛物线的对称轴为:直线,
由题意得:,
解得:,
一次函数的表达式为:,
;
由图象得:不等式的解集为:.
19.
20.证明:如图,连接,,
是直径,
,
与都是直角三角形,
在与中,
,
≌,
,
平分;
解:如图,连接,设与交于点,
由可知,垂直平分,
,
在中,由勾股定理得,
,
设,则,
在中,由勾股定理得,
,
,
解得,
的半径为.
21.解:由题意可得,,,
,
,即,解得:,
;
根据题意有,
,
,即,
,
,
当时,,取得最大值,最大值为,
的最大值为.
22.解:如图,连接.
,
为中点,
,
,
又,
设,则.
在中,根据勾股定理得:,
解得.
答:此圆弧形拱桥的半径为.
此货船不能顺利通过这座拱桥,理由如下:
连接,
,船舱顶部为长方形并高出水面,
,
,
在中,由勾股定理得:,
.
此货船不能顺利通过这座拱桥.
23.解:小球运动的水平距离为时,小球达到最大高度,
抛物线的对称轴为:直线.
.
解得:.
由题意得:抛物线上点的坐标为.
.
抛物线的解析式为:.
当时,.
答:小球达到的最大高度为;
由题意得:点的坐标为,点的坐标为.
抛物线上点的坐标为,
.
抛物线的解析式为:.
抛物线经过点.
.
解得:.
抛物线经过点.
.
解得:.
要使小球落人筐中,的取值范围为:.
24.解:,
函数顶点坐标为;
函数顶点在轴上,
,
解得或,
,
,
二次函数解析式为,
对称轴为直线,
当时,即,此时在对称轴右侧,
,
当时,有最大值,即,
解得,舍去,
;
当时,在对称轴左侧,
,
当时,有最大值,即,
解得,舍去,
;
当时,此时有最大值,与题矛盾,故舍去;
综上所述,或;
由知二次函数图象的对称轴为,且开口向下,
二次函数图象上的两点,,时,始终有成立,
点到对称轴的距离小于或等于点到对称轴的距离,
,即,
,
即,
,
,
,
即,
,
解得:,
,
.
第1页,共1页
同课章节目录
