北师大版五年级上册数学图形与几何(课件)(共56张PPT)
文档属性
| 名称 | 北师大版五年级上册数学图形与几何(课件)(共56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 06:51:10 | ||
图片预览











文档简介
(共56张PPT)
五年级上册总复习·图形与几何
五年级数学·上 新课标[北师]
单 元 复 习
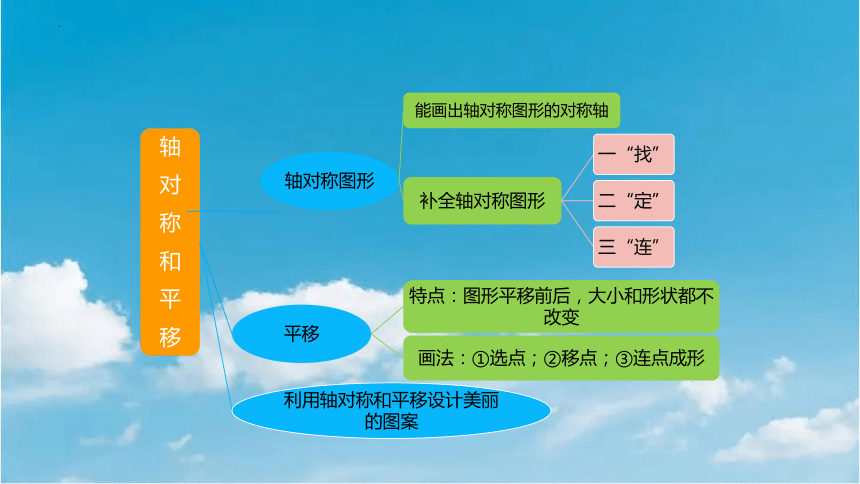
图形与几何之轴对称与平移
找找生活中的轴对称?
生活中像蝴蝶、天安门城楼这样,左右两边一样,就是对称的。
图形沿着一条直线对折后,两边完全重合,这样的图形叫做轴对称图形。
一、轴对称图形
轴对称图形的特征:
轴对称图形的对称点到对称轴的距离相等
连接对称点的连线与对称轴垂直。
补全轴对称图形的方法:
一“找”,找出图形上每条线段的端点
二“定”,根据对称轴确定每一个端点的对称点
三“连”,依次连接这些对称点,得到轴对称图形的另一半
二、平移
图形平移前后,有什么特点呢?
大小和形状都不改变
在画平移后的图形时,要注意些什么呢?
平移的距离是对应点之间的方格数,而不是平移前后两个图形之间的方格数
一、填空题。
轴对称
对称轴
直线
平移
二、选择题
①下列图形中,不是轴对称图形的是( )
A.等腰三角形 B.正方形
C.平行四边形 D.等腰梯形
②长方形有( )条对称轴,正方形有( )条对称轴,等边三角形有( )条对称轴。
A.1 B.2 C.3 D.4
③如图,下面四个图案可由图形(1)平移得到的是( )
C
B
D
C
B
三、判断。(对的打“√”,错的打“×”)
√
√
√
×
△
△
△
四、下列图形是轴对称图形吗?如果是,请画出它的对称轴。
5
2
4
五、
无数
1
2
猫
8
花瓶
衬衫
七、按要求画一画:将三角形先向上平移2格,再向左平移5格。
单 元 复 习
图形与几何之图形的规律
在摆图形中发现规律
摆一摆,想一想,填一填。
(1)摆1个六边形需要( )根小棒;
摆2个六边形需要( )根小棒;
摆3个六边形需要( )根小棒;
摆4个六边形需要( )根小棒。
21
6
11
16
(2)通过观察发现,除了摆第1个六边形用了6根小棒外,每多摆1个六边形,就增加( )根小棒。
(3)照这样摆下去,摆10个六边形需要( )根小棒;摆n个六边形需要( )根小棒。
(4)照这样摆下去,81根小棒可以摆( )个六边形。
5
51
5n+1
16
单 元 复 习
图形与几何之多边形的面积
多边形的面积
比较图形的面积
多边形的面积
比较图形的面积
计算图形的面积
作图形的高
平行四边形的面积
三角形的面积
梯形的面积
S=ah
实际应用
S=ah÷ 2
实际应用
——
S=(a+b)h÷ 2
知识网络
1.数方格法。
这是最基本的方法,借助方格纸,直接判断图形面积的大小。
2.平移、重合进行比较。
通过平移或旋转后再平移,使图形重叠进行比较。
3.直接计算图形的面积进行比较。
复习导入
1.三角形只有三条高,平行四边形和梯形都有无数条高。
2.高和底之间的关系是对应的。
3.用三角板画平行四边形、梯形、三角形的高。
从一个顶点向底引垂线,与底垂直的线段就是高。
注意:平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高。
复习导入
平行四边形面积计算公式是“底×高”,用字母表示S=ah。
1.平行四边形面积计算公式。
复习导入
2.三角形面积计算公式。
三角形面积计算公式是底×高÷2,用字母表示是S=ah÷2。
复习导入
3.梯形面积计算公式。
梯形的面积计算公式是(上底+下底)×高÷2,用字母表示是S=(a+b)×h÷2。
复习导入
一块平行四边形的广告牌,底是11.5 m,高是2 m。粉刷这块广告牌每平方米要用油漆0.6 kg,至少需要准备多少千克油漆?
首先要知道平行四边形的面积,再乘每平方米用的油漆质量,即可求出需要多少千克油漆。
11.5×2×0.6=13.8(千克)
答:至少需要准备13.8千
克油漆。
习
练
分析
把一个平行四边形剪成两个完全相同的图形,且没有剩余,可以剪成什么样的图形?
(1)如图①,沿对角线剪开,可以剪成两个完全相同的三角形。
(2)如图②,可以剪成两个相同的梯形,注意要使AB=CD。
(3)如图③,连接两条对边的中点,可以剪成两个完全相同的平行四边形。
习
练
分析
解答:
三角形、梯形或平行四边形。
把一个平行四边形剪成两个完全相同的图形,且没有剩余,可以剪成什么样的图形?
习
练
下图是一块三角形菜地,这块菜地的面积是多少平方米?
求三角形菜地的面积即求该三角形的面积,运用公式计算即可。
62×35÷2=1085(平方米)
答:这块菜地的面积是1085平方米。
习
练
分析
一个三角形的底边长10 cm,若高不变,底延长5 cm,则面积增加10 cm2,原来三角形的面积是多少?
原来的三角形与增加的三角形的高是相等的,可以通过增加的三角形的面积与延长的底求出高,再求出原来三角形的面积。
10×2÷5×10÷2=20(cm2)
分析
习
练
如下图,李叔叔在墙的一侧用篱笆围成了一个鸡舍。篱笆长42 m,这个鸡舍的面积是多少?
这个鸡舍是一个梯形,用篱笆的长减去鸡舍的高,就是梯形上、下底的和,根据梯形的面积公式,就能求出鸡舍的面积。
(42-12)×12÷2=180(平方米)
习
练
分析
如下图,梯形的面积是128 cm2,上底是12 cm,高是8 cm。求阴影部分的面积。
阴影部分是一个三角形,它的高就是梯形的高,它的底就是梯形的下底。再运用三角形面积计算公式即可求解。
(128×2÷8-12)×8÷2=80(平方厘米)
分析
习
练
三角形的面积等于平行四边形面积的一半。( √ )
三角形的面积是与它等底等高的平行四边形面积的一半。
正确解答:×
习
练
分析
复习导入
梯形的高不变,上底和下底变了,面积一定会发生改变。( √ )
梯形的面积=(上底+下底)×高÷2
正确解答: ×
分析
习
练
如下图,三个等底的三角形面积不相等。(×)
如下图,等底等高的三角形面积相等。
正确解答:√
习
练
分析
如下图,平行四边形一条底边长18 cm,两条高分别是15 cm和12 cm,这个平行四边形的面积是多少平方厘米?
18×15=270(平方厘米)
正确解答:18×12=216(平方厘米)
计算平行四边形的面积时,要用对应的底和高相乘。
分析
习
练
单 元 复 习
图形与几何之组合图形的面积
《组合图形的面积》复习课
知识梳理
组合图形的面积
组合图形的面积
不规则图形的面积
认识较大的面积单位
将组合图形转化为已学过的图形,再计算。
非基本图形的面积
1平方千米=100公顷
1公顷=10000平方米
1平方千米=100 0000平方米
方法1:数格子。
方法2:看作某个基本图形的近似图形,利用图形的面积公式求出面积。
小试牛刀
1.计算下面组合图形的面积,你有几种方法?
方法1:长方形+梯形
长方形的面积:6×5=30(cm2)
梯形的面积:(5+10)×(12-6)÷2=45(cm2)
组合图形的面积:30+45=75(cm2)
1.计算下面组合图形的面积,你有几种方法?
方法1:长方形+梯形
方法2:三角形+长方形
三角形的面积:(12-6)×(10-5)÷2=15(cm )
长方形的面积:12×5=60(cm )
组合图形的面积:15+60=75(cm )
小试牛刀
三角形的面积:10×(12-6)÷2=30(cm2)
梯形的面积:(6+12)×5÷2=45(cm2)
组合图形的面积:30+45=75(cm2)
1.计算下面组合图形的面积,你有几种方法?
方法2:三角形+长方形
方法3:三角形+梯形
方法1:长方形+梯形
小试牛刀
长方形的面积:12×10=120(cm2)
梯形的面积:(6+12)×(10-5)÷2=45(cm2)
组合图形的面积:120-45=75(cm2)
1.计算下面组合图形的面积,你有几种方法?
方法1:长方形+梯形
方法2:三角形+长方形
方法3:三角形+梯形
方法4:长方形-梯形
小试牛刀
2.有一块平行四边形麦田,底是250米,对应的高是84米,今年一共收小麦14.7吨。这块麦田有所少公顷,今年平均每公顷收小麦多少吨?
250×84=21000(m2)
21000平方米=2.1公顷
14.7÷2.1=7(吨)
答:今年平均每公顷收小麦7吨。
小试牛刀
3.估计下面图形的面积。(每个小方格的边长表示1cm)
面积约为 cm
面积约为 cm
小试牛刀
小试牛刀
平方千米 公顷 平方米 平方分米 平方厘米
100
100
100
10000
4.我们学过哪些面积单位?它们的进率是多少呢?
《鸡兔同笼》复习课
30000m2=( )公顷
3
6km2=( )公顷
0.64km2=( )m2
4800000m2=( )km2
600
640000
4.8
1.填一填
小试牛刀
2.在横线上填上合适的面积单位(m2、公顷、km2)。
圆明园占地面积约350 。
奥林匹克森林公园占地面积约6.8 。
故宫占地面积约
720000 。
公顷
km2
m2
小试牛刀
3.一个足球场,长110m、宽90m,它的面积是多少平方米?1km2大约相当于多少个这样的足球场?
110×90=9900(m2)
9900m2≈10000m2
1km2=1000000m2
1000000÷10000=100(个)
答:它的面积是9900平方米。1km2大约相当于100个这样的足球场。
小试牛刀
单 元 复 习
图形与几何之鸡兔同笼
《鸡兔同笼》复习课
知识梳理
鸡兔同笼解决方法
逐一列表法
取中列表法
假设法
列表法
跳跃列表法
假设全是兔
假设全是鸡
方程法
设未知数,根据等量关系列方程
1.《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
鸡有几只 兔有几只 腿有多少条
17
18
20
15
100
22
13
96
ⅹ
ⅹ
106
ⅹ
还可以先假设鸡兔只数差不多。
腿还多,兔子数应该减少。
差不多了,再调一点儿。
23
12
94
√
取中列表法
小试牛刀
1.《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
假设全是鸡,35只鸡一共几条腿?
35×2=70(条)
少了几条腿?
94-70=24(条)
将一只鸡换成一只兔,就增加几条腿?
4-2=2(条)
需要换几只兔才能增加24条腿?
24÷2=12(只)
兔子的数量
鸡有多少只?
35-12=23(只)
鸡的数量
答:鸡有23只,兔有12只
假设法
小试牛刀
1.《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
小试牛刀
方程法
解:设鸡有x只,则兔有(35-x)只.
2x+4×(35-x)=94
解得 x=23
35-23=12(只)
答:鸡有23只,兔有12只
鸡的数量+兔的数量=35
鸡腿的数量+兔腿的数量=94
2.全班一共有38人,共租了8条船,每条船都坐满了。大小船各租了几条?(大船乘6人,小船乘4人)
小试牛刀
假设都是小船
8×4=32(人)
38-32=6(人)
6-4=2(人)
6÷2=3(条)
小船:
8-3=5(条)
大船:
答:大船租了3条,小船租了5条
假设都是大船
8×6=48(人)
48—38=10(人)
6—4=2(人)
10÷2=5(条)
大船:
8-5=3(条)
小船:
小试牛刀
2.乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元,1角和5角的硬币各有多少枚?
27×1=27(角)
51-27=24(角)
5-1=4(角)
24÷4=6(枚)
27-6=21(枚)
假设都是1角的硬币
答:1角的硬币有21枚,5角的硬币有6枚
假设都是5角的硬币
5×27=135(角)
135-51=84(角)
5-1=4(角)
84÷4=21(枚)
27-21=6(枚)
谢谢大家
五年级上册总复习·图形与几何
五年级数学·上 新课标[北师]
单 元 复 习
图形与几何之轴对称与平移
找找生活中的轴对称?
生活中像蝴蝶、天安门城楼这样,左右两边一样,就是对称的。
图形沿着一条直线对折后,两边完全重合,这样的图形叫做轴对称图形。
一、轴对称图形
轴对称图形的特征:
轴对称图形的对称点到对称轴的距离相等
连接对称点的连线与对称轴垂直。
补全轴对称图形的方法:
一“找”,找出图形上每条线段的端点
二“定”,根据对称轴确定每一个端点的对称点
三“连”,依次连接这些对称点,得到轴对称图形的另一半
二、平移
图形平移前后,有什么特点呢?
大小和形状都不改变
在画平移后的图形时,要注意些什么呢?
平移的距离是对应点之间的方格数,而不是平移前后两个图形之间的方格数
一、填空题。
轴对称
对称轴
直线
平移
二、选择题
①下列图形中,不是轴对称图形的是( )
A.等腰三角形 B.正方形
C.平行四边形 D.等腰梯形
②长方形有( )条对称轴,正方形有( )条对称轴,等边三角形有( )条对称轴。
A.1 B.2 C.3 D.4
③如图,下面四个图案可由图形(1)平移得到的是( )
C
B
D
C
B
三、判断。(对的打“√”,错的打“×”)
√
√
√
×
△
△
△
四、下列图形是轴对称图形吗?如果是,请画出它的对称轴。
5
2
4
五、
无数
1
2
猫
8
花瓶
衬衫
七、按要求画一画:将三角形先向上平移2格,再向左平移5格。
单 元 复 习
图形与几何之图形的规律
在摆图形中发现规律
摆一摆,想一想,填一填。
(1)摆1个六边形需要( )根小棒;
摆2个六边形需要( )根小棒;
摆3个六边形需要( )根小棒;
摆4个六边形需要( )根小棒。
21
6
11
16
(2)通过观察发现,除了摆第1个六边形用了6根小棒外,每多摆1个六边形,就增加( )根小棒。
(3)照这样摆下去,摆10个六边形需要( )根小棒;摆n个六边形需要( )根小棒。
(4)照这样摆下去,81根小棒可以摆( )个六边形。
5
51
5n+1
16
单 元 复 习
图形与几何之多边形的面积
多边形的面积
比较图形的面积
多边形的面积
比较图形的面积
计算图形的面积
作图形的高
平行四边形的面积
三角形的面积
梯形的面积
S=ah
实际应用
S=ah÷ 2
实际应用
——
S=(a+b)h÷ 2
知识网络
1.数方格法。
这是最基本的方法,借助方格纸,直接判断图形面积的大小。
2.平移、重合进行比较。
通过平移或旋转后再平移,使图形重叠进行比较。
3.直接计算图形的面积进行比较。
复习导入
1.三角形只有三条高,平行四边形和梯形都有无数条高。
2.高和底之间的关系是对应的。
3.用三角板画平行四边形、梯形、三角形的高。
从一个顶点向底引垂线,与底垂直的线段就是高。
注意:平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高。
复习导入
平行四边形面积计算公式是“底×高”,用字母表示S=ah。
1.平行四边形面积计算公式。
复习导入
2.三角形面积计算公式。
三角形面积计算公式是底×高÷2,用字母表示是S=ah÷2。
复习导入
3.梯形面积计算公式。
梯形的面积计算公式是(上底+下底)×高÷2,用字母表示是S=(a+b)×h÷2。
复习导入
一块平行四边形的广告牌,底是11.5 m,高是2 m。粉刷这块广告牌每平方米要用油漆0.6 kg,至少需要准备多少千克油漆?
首先要知道平行四边形的面积,再乘每平方米用的油漆质量,即可求出需要多少千克油漆。
11.5×2×0.6=13.8(千克)
答:至少需要准备13.8千
克油漆。
习
练
分析
把一个平行四边形剪成两个完全相同的图形,且没有剩余,可以剪成什么样的图形?
(1)如图①,沿对角线剪开,可以剪成两个完全相同的三角形。
(2)如图②,可以剪成两个相同的梯形,注意要使AB=CD。
(3)如图③,连接两条对边的中点,可以剪成两个完全相同的平行四边形。
习
练
分析
解答:
三角形、梯形或平行四边形。
把一个平行四边形剪成两个完全相同的图形,且没有剩余,可以剪成什么样的图形?
习
练
下图是一块三角形菜地,这块菜地的面积是多少平方米?
求三角形菜地的面积即求该三角形的面积,运用公式计算即可。
62×35÷2=1085(平方米)
答:这块菜地的面积是1085平方米。
习
练
分析
一个三角形的底边长10 cm,若高不变,底延长5 cm,则面积增加10 cm2,原来三角形的面积是多少?
原来的三角形与增加的三角形的高是相等的,可以通过增加的三角形的面积与延长的底求出高,再求出原来三角形的面积。
10×2÷5×10÷2=20(cm2)
分析
习
练
如下图,李叔叔在墙的一侧用篱笆围成了一个鸡舍。篱笆长42 m,这个鸡舍的面积是多少?
这个鸡舍是一个梯形,用篱笆的长减去鸡舍的高,就是梯形上、下底的和,根据梯形的面积公式,就能求出鸡舍的面积。
(42-12)×12÷2=180(平方米)
习
练
分析
如下图,梯形的面积是128 cm2,上底是12 cm,高是8 cm。求阴影部分的面积。
阴影部分是一个三角形,它的高就是梯形的高,它的底就是梯形的下底。再运用三角形面积计算公式即可求解。
(128×2÷8-12)×8÷2=80(平方厘米)
分析
习
练
三角形的面积等于平行四边形面积的一半。( √ )
三角形的面积是与它等底等高的平行四边形面积的一半。
正确解答:×
习
练
分析
复习导入
梯形的高不变,上底和下底变了,面积一定会发生改变。( √ )
梯形的面积=(上底+下底)×高÷2
正确解答: ×
分析
习
练
如下图,三个等底的三角形面积不相等。(×)
如下图,等底等高的三角形面积相等。
正确解答:√
习
练
分析
如下图,平行四边形一条底边长18 cm,两条高分别是15 cm和12 cm,这个平行四边形的面积是多少平方厘米?
18×15=270(平方厘米)
正确解答:18×12=216(平方厘米)
计算平行四边形的面积时,要用对应的底和高相乘。
分析
习
练
单 元 复 习
图形与几何之组合图形的面积
《组合图形的面积》复习课
知识梳理
组合图形的面积
组合图形的面积
不规则图形的面积
认识较大的面积单位
将组合图形转化为已学过的图形,再计算。
非基本图形的面积
1平方千米=100公顷
1公顷=10000平方米
1平方千米=100 0000平方米
方法1:数格子。
方法2:看作某个基本图形的近似图形,利用图形的面积公式求出面积。
小试牛刀
1.计算下面组合图形的面积,你有几种方法?
方法1:长方形+梯形
长方形的面积:6×5=30(cm2)
梯形的面积:(5+10)×(12-6)÷2=45(cm2)
组合图形的面积:30+45=75(cm2)
1.计算下面组合图形的面积,你有几种方法?
方法1:长方形+梯形
方法2:三角形+长方形
三角形的面积:(12-6)×(10-5)÷2=15(cm )
长方形的面积:12×5=60(cm )
组合图形的面积:15+60=75(cm )
小试牛刀
三角形的面积:10×(12-6)÷2=30(cm2)
梯形的面积:(6+12)×5÷2=45(cm2)
组合图形的面积:30+45=75(cm2)
1.计算下面组合图形的面积,你有几种方法?
方法2:三角形+长方形
方法3:三角形+梯形
方法1:长方形+梯形
小试牛刀
长方形的面积:12×10=120(cm2)
梯形的面积:(6+12)×(10-5)÷2=45(cm2)
组合图形的面积:120-45=75(cm2)
1.计算下面组合图形的面积,你有几种方法?
方法1:长方形+梯形
方法2:三角形+长方形
方法3:三角形+梯形
方法4:长方形-梯形
小试牛刀
2.有一块平行四边形麦田,底是250米,对应的高是84米,今年一共收小麦14.7吨。这块麦田有所少公顷,今年平均每公顷收小麦多少吨?
250×84=21000(m2)
21000平方米=2.1公顷
14.7÷2.1=7(吨)
答:今年平均每公顷收小麦7吨。
小试牛刀
3.估计下面图形的面积。(每个小方格的边长表示1cm)
面积约为 cm
面积约为 cm
小试牛刀
小试牛刀
平方千米 公顷 平方米 平方分米 平方厘米
100
100
100
10000
4.我们学过哪些面积单位?它们的进率是多少呢?
《鸡兔同笼》复习课
30000m2=( )公顷
3
6km2=( )公顷
0.64km2=( )m2
4800000m2=( )km2
600
640000
4.8
1.填一填
小试牛刀
2.在横线上填上合适的面积单位(m2、公顷、km2)。
圆明园占地面积约350 。
奥林匹克森林公园占地面积约6.8 。
故宫占地面积约
720000 。
公顷
km2
m2
小试牛刀
3.一个足球场,长110m、宽90m,它的面积是多少平方米?1km2大约相当于多少个这样的足球场?
110×90=9900(m2)
9900m2≈10000m2
1km2=1000000m2
1000000÷10000=100(个)
答:它的面积是9900平方米。1km2大约相当于100个这样的足球场。
小试牛刀
单 元 复 习
图形与几何之鸡兔同笼
《鸡兔同笼》复习课
知识梳理
鸡兔同笼解决方法
逐一列表法
取中列表法
假设法
列表法
跳跃列表法
假设全是兔
假设全是鸡
方程法
设未知数,根据等量关系列方程
1.《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
鸡有几只 兔有几只 腿有多少条
17
18
20
15
100
22
13
96
ⅹ
ⅹ
106
ⅹ
还可以先假设鸡兔只数差不多。
腿还多,兔子数应该减少。
差不多了,再调一点儿。
23
12
94
√
取中列表法
小试牛刀
1.《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
假设全是鸡,35只鸡一共几条腿?
35×2=70(条)
少了几条腿?
94-70=24(条)
将一只鸡换成一只兔,就增加几条腿?
4-2=2(条)
需要换几只兔才能增加24条腿?
24÷2=12(只)
兔子的数量
鸡有多少只?
35-12=23(只)
鸡的数量
答:鸡有23只,兔有12只
假设法
小试牛刀
1.《孙子算经》中的原题是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
小试牛刀
方程法
解:设鸡有x只,则兔有(35-x)只.
2x+4×(35-x)=94
解得 x=23
35-23=12(只)
答:鸡有23只,兔有12只
鸡的数量+兔的数量=35
鸡腿的数量+兔腿的数量=94
2.全班一共有38人,共租了8条船,每条船都坐满了。大小船各租了几条?(大船乘6人,小船乘4人)
小试牛刀
假设都是小船
8×4=32(人)
38-32=6(人)
6-4=2(人)
6÷2=3(条)
小船:
8-3=5(条)
大船:
答:大船租了3条,小船租了5条
假设都是大船
8×6=48(人)
48—38=10(人)
6—4=2(人)
10÷2=5(条)
大船:
8-5=3(条)
小船:
小试牛刀
2.乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元,1角和5角的硬币各有多少枚?
27×1=27(角)
51-27=24(角)
5-1=4(角)
24÷4=6(枚)
27-6=21(枚)
假设都是1角的硬币
答:1角的硬币有21枚,5角的硬币有6枚
假设都是5角的硬币
5×27=135(角)
135-51=84(角)
5-1=4(角)
84÷4=21(枚)
27-21=6(枚)
谢谢大家
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
