5.1.2垂线(1)课件
图片预览




文档简介
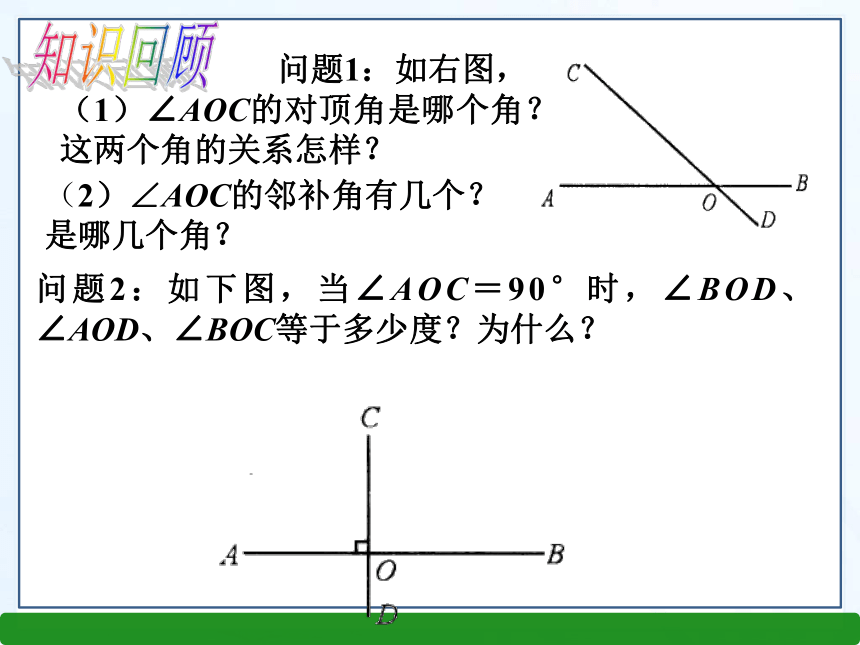
课件26张PPT。5.1.2 垂线(1)义务教育教科书(RJ)七年级数学下册第五章 相交线与平行线 问题1:如右图,
(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
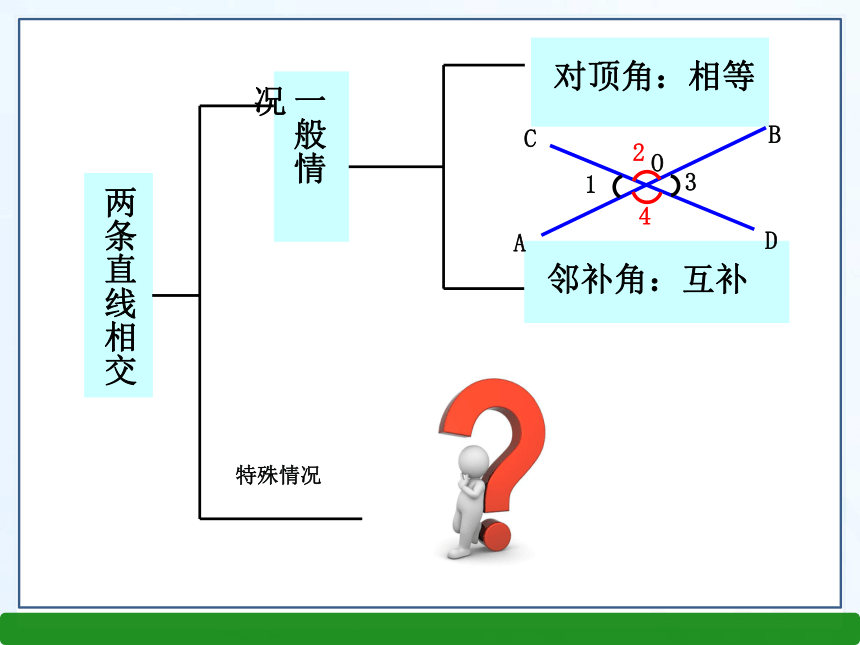
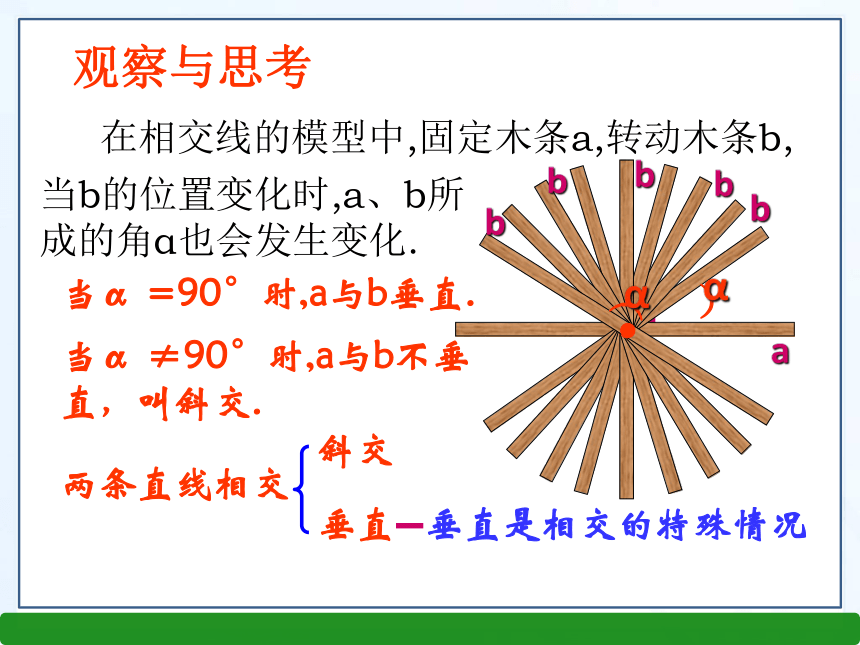
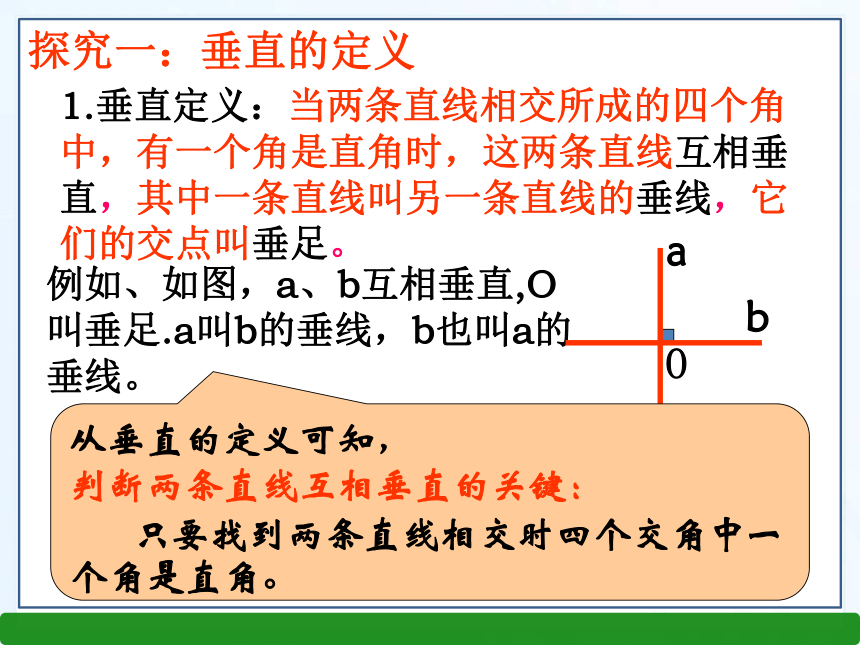
(2)∠AOC的邻补角有几个?是哪几个角? 问题2:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么? 知识回顾特殊情况BACDO1234入水姿势情境引入 观察:两条直线相交形成4个角,若固定木条a,旋转木条b,当b的位置发生变化时,a、b所成的角也会随之变化,其中有一个特殊的位置: =90° . 新知探究在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况)α abbbbb)α 观察与思考1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。探究一:垂直的定义日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?十字路口的两条道路围棋盘的横线和竖线铅垂线和水平线生活中的垂直图1图4图3图2ba1)图形:Oα 2)文字:a、b互相垂直, 垂足为O3)符号:a⊥b或b⊥a,
若要强调垂足,
则记为:a⊥b, 垂足为O 探究二:垂直的表示ABCDO书写形式:如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式:反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。②性质:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)探究三:垂直的书写形式做一做
1.两条直线相交所成的四个角中,下列条件中能断定两条直线垂直的是( )
(A)有一个角为90° (B)有两个角相等
(C) 有三个角相等 (D)有四个角相等
(E)有四对邻补角 (F)有一对对顶角互补(G)有一对邻补角相等 (H)有两组角相等 A C D F G2.如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35°, ∠2=55°,则OE与AB的位置关系
是 . 切记:要证垂直必先想到直角(90°)联想数学OE⊥ABACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55° 探究四: 例题例1 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.(对顶角相等)探究五:垂线的画法问题:
怎么样画垂线?1.垂线的画法:问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AB是过点A的直线l的垂线.思考:
结论: 过一点有且只有一条直线与已知直线垂直。(1)画已知直线l的垂线能画几条?
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条? 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.两条直线相交一般情况垂线对顶角:相等邻补角:互补垂线的存在性和唯一性
特殊情况相交成直角知识梳理 回忆两条直线相交这部分知识,你们能够把它们画成一个知识结构图吗? 1.过点P 向线段AB 所在直线引垂线,正确的是( ). A B C D
C随堂练习2.如何画一条线段或一条射线的垂线? 画已知线段、射线的垂线其实
就是经过已知点作已知线段、射线
所在的直线的垂线. 3.若直线m、n相交于点O,
∠1=90°,则__________。
4.若直线AB、CD相交于点O,
且AB⊥CD,那么∠BOD=____。
5.如图,BO⊥AO,∠BOC
与∠BOA的度数之比为1:5,
那么∠COA=_____,
∠BOC的补角为______度。m⊥n90°72°162
(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的邻补角有几个?是哪几个角? 问题2:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么? 知识回顾特殊情况BACDO1234入水姿势情境引入 观察:两条直线相交形成4个角,若固定木条a,旋转木条b,当b的位置发生变化时,a、b所成的角也会随之变化,其中有一个特殊的位置: =90° . 新知探究在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况)α abbbbb)α 观察与思考1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。探究一:垂直的定义日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?十字路口的两条道路围棋盘的横线和竖线铅垂线和水平线生活中的垂直图1图4图3图2ba1)图形:Oα 2)文字:a、b互相垂直, 垂足为O3)符号:a⊥b或b⊥a,
若要强调垂足,
则记为:a⊥b, 垂足为O 探究二:垂直的表示ABCDO书写形式:如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式:反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。②性质:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)探究三:垂直的书写形式做一做
1.两条直线相交所成的四个角中,下列条件中能断定两条直线垂直的是( )
(A)有一个角为90° (B)有两个角相等
(C) 有三个角相等 (D)有四个角相等
(E)有四对邻补角 (F)有一对对顶角互补(G)有一对邻补角相等 (H)有两组角相等 A C D F G2.如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35°, ∠2=55°,则OE与AB的位置关系
是 . 切记:要证垂直必先想到直角(90°)联想数学OE⊥ABACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55° 探究四: 例题例1 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.(对顶角相等)探究五:垂线的画法问题:
怎么样画垂线?1.垂线的画法:问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AB是过点A的直线l的垂线.思考:
结论: 过一点有且只有一条直线与已知直线垂直。(1)画已知直线l的垂线能画几条?
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条? 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.两条直线相交一般情况垂线对顶角:相等邻补角:互补垂线的存在性和唯一性
特殊情况相交成直角知识梳理 回忆两条直线相交这部分知识,你们能够把它们画成一个知识结构图吗? 1.过点P 向线段AB 所在直线引垂线,正确的是( ). A B C D
C随堂练习2.如何画一条线段或一条射线的垂线? 画已知线段、射线的垂线其实
就是经过已知点作已知线段、射线
所在的直线的垂线. 3.若直线m、n相交于点O,
∠1=90°,则__________。
4.若直线AB、CD相交于点O,
且AB⊥CD,那么∠BOD=____。
5.如图,BO⊥AO,∠BOC
与∠BOA的度数之比为1:5,
那么∠COA=_____,
∠BOC的补角为______度。m⊥n90°72°162
