24.1圆的有关性质同步练习(含答案)
文档属性
| 名称 | 24.1圆的有关性质同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1000.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.1圆的有关性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,内接于,是直径.若,则直径的长为( )
A.15 B. C.12 D.
2.如图,AB是⊙O的真径,点C、D在⊙O上,若∠ABD=50°.则∠BCD的度数为( )
A.25° B.30° C.35° D.40°
3.如图,是的两条弦,于点D,于点E,连结,.若,则的度数为( )
A. B. C. D.
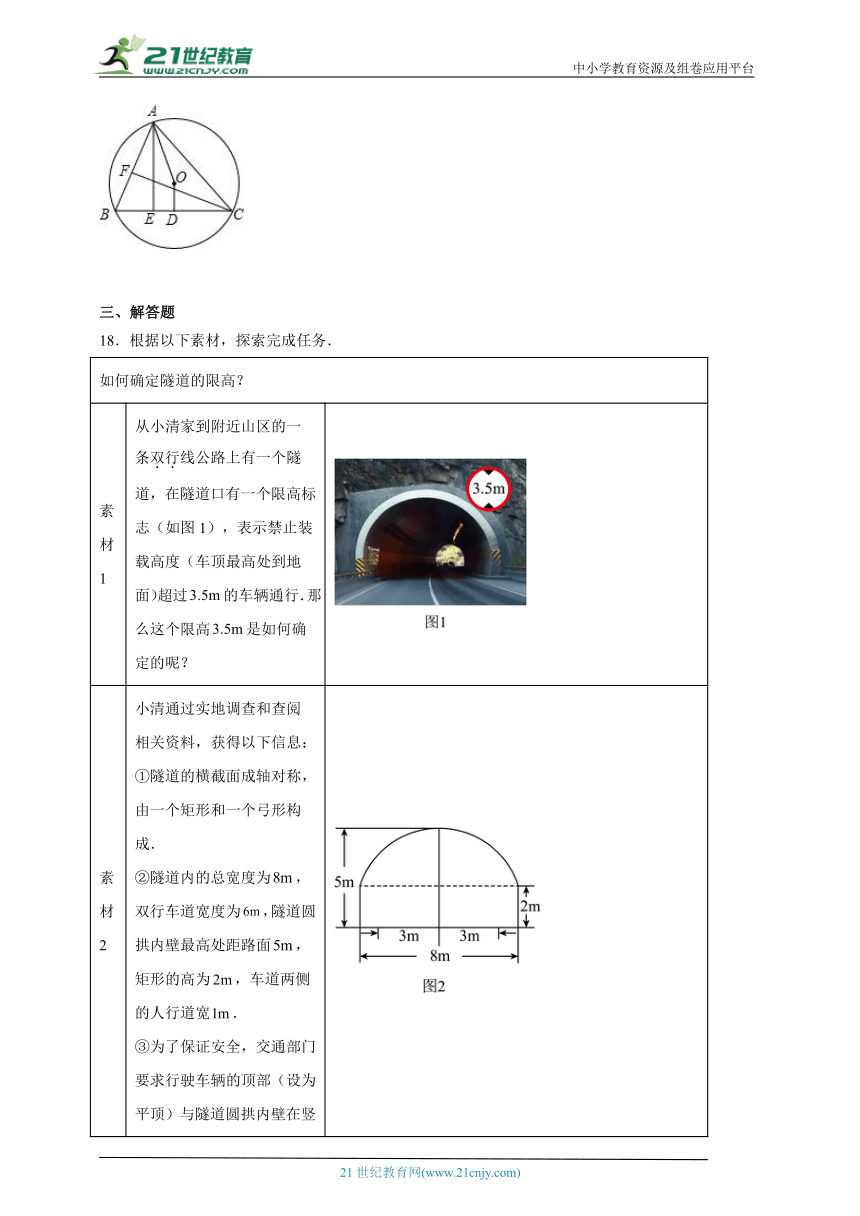
4.如图,中,弦与交于点,点为中点,,,则的度数是( )
A. B. C. D.
5.如图,是四边形的外接圆的直径,点E 在上,连接,若,则 的度数为( )
A. B. C. D.
6.下列表述不正确的有( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④半圆是弧;⑤圆内接四边形对角互补.
A.1个
B.2个
C.3个
D.4个
7.如图,点A,B,C在上,,则的度数是( )
A. B. C. D.
8.有下列说法:①弦是直径 ②半圆是弧 ③圆中最长的弦是直径 ④半圆是圆中最长的弧 ⑤平分弦的直径垂直于弦,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
9.下列命题中,正确的是( )
①顶点在圆心的角是圆心角;②相等的圆心角,所对的弧也相等;③两条弦相等,它们所对的弧也相等;④在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.①和③
C.①和④ D.①、②、③、④
10.如图,是的直径,,是上的两点,且,则的度数为( )
A.42° B.84° C.90° D.96°
11.如图,AB是的直径,C、D是圆上两点,连接AC,AD,CD.若∠CAB=35°,则∠ADC的度数为( )
A.55° B.45° C.35° D.25°
12.如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A.OM的长 B.OM的长 C.2OM的长 D.CD的长
二、填空题
13.如图,ABC是⊙O的内接三角形,OD⊥BC于点D.下面是借助直尺,画出ABC中∠BAC的平分线的步骤:
①延长OD交于点M;
②连接AM交BC于点N.
所以∠BAN=∠CAN.
即线段AN为所求ABC中∠BAC的平分线.
请回答,得到∠BAN=∠CAN的依据是 .
14.如图,是圆O的直径,点C、D是半圆的三等分点,与交于点E.如果,那么 .
15.如图,已知正方形ABCD的各个顶点A、B、C、D都在⊙O上,如果P是的中点,PD与AB交于E点,那么= .
16.在同圆中,若AB和CD都是劣弧,且,那么成立的是 (填序号).
① ② ③ ④不确定
17.如图,内接于,,是的中点,且,分别是边上的高,则的大小 度.
三、解答题
18.根据以下素材,探索完成任务.
如何确定隧道的限高?
素材1 从小清家到附近山区的一条双行线公路上有一个隧道,在隧道口有一个限高标志(如图1),表示禁止装载高度(车顶最高处到地面)超过的车辆通行.那么这个限高是如何确定的呢?
素材2 小清通过实地调查和查阅相关资料,获得以下信息: ①隧道的横截面成轴对称,由一个矩形和一个弓形构成. ②隧道内的总宽度为,双行车道宽度为,隧道圆拱内壁最高处距路面,矩形的高为,车道两侧的人行道宽. ③为了保证安全,交通部门要求行驶车辆的顶部(设为平顶)与隧道圆拱内壁在竖直方向上的高度差相差最少.
问题解决
任务1 计算半径 求图1中弓形所在圆的半径.
任务2 确定限高 如图2,在安全的条件下,的限高是如何确定的?请通过计算说明理由.(参考数据:,结果保留一位小数)
任务3 尝试设计 如果要使高度不超过,宽为的货车能顺利通过这个隧道,且不改变隧道内的总宽度()和矩形的高(),如何设计隧道的弓形部分(求弓形所在圆的半径至少为多少米?)(参考数据:,结果保留一位小数)
19.阅读与思考
如图是小亮同学的数学日记,请仔细阅读,并完成相应的任务,
×年×月×日星期日
只用尺规也能判断两条线是否垂直
如图1,点是直线MN上一点,为射线,现在需要判断和是否垂直,然而我手头只有直尺和圆规,该怎么办呢?
我发现在初中三年的学习中很多知识都和直角有关,经过思考我想到了以下三个办法:
办法一:如图2,在射线上任取一点A,以A为圆心,大于长为半径作弧交于点B,点C,连接,若则,即.
办法二:如图3,在,上分别取点A,B,以AB为直径画圆,若点O在圆上,则.
办法三:如图4,在上任取一点A,以为边在作等边,延长交于点C,若,则,即.
还有只用尺规就可以判断和是否垂直的办法吗?……
任务:
(1)填空:“办法一”依据的数学定理是 ;“办法二”依据的数学定理是 ;
(2)请说明“办法三”尺规作图的合理性;
(3)在下图中再设计一种不同的方法探究与是否互相垂直(要求:尺规作图,保留作痕迹并描述探究的方法)
20.[发现问题]爱好数学的小明在做作业时碰到这样的一道题目∶
如图①,点O为坐标原点,的半径为1,点.动点B在上,连结,作等边(A,B,C 为顺时针顺序),求的最大值.
[解决问题]小明经过多次的尝试与探索,终于得到解题思路∶在图①中,连接,以为边在的左侧作等边三角形,连接.
(1)请你找出图中与相等的线段,并说明理由;
(2)线段的最大值为 .
[灵活运用]
(3)如图②,在平面直角坐标系中,点A的坐标为,点B的坐标为,点P为线段外一动点,且,以P为旋转中心,把逆时针旋转得,连接,求长的最大值及此时点P的坐标.
[迁移拓展]
(4)如图③,,点D是以为直径的半圆上不同于B、C的一个动点,以为边作等边,请直接写出的最值.
21.一辆卡车装满货物后,它的高比宽多,且恰好通过如图所示的隧道(上部为半圆形).卡车有多高?(结果精确到)
22.如图,圆环的内外圈用铁丝围成,其中大圆半径比小圆半径的2倍多1米,如果圆环的面积等于平方米,求围成圆环铁丝的总长度.
23.如图,是三角形的外接圆,是的直径,于点E.
(1)求证:;
(2)若长为8,,求的半径长.
24.已知如图,内接于,为直径,于点D,于点F.
(1)求证:;
(2)当点C是的中点时,求证:.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C C C C B C B
题号 11 12
答案 A B
1.B
2.D
3.B
4.C
5.C
6.C
7.C
8.B
9.C
10.B
11.A
12.B
13.在同圆或等圆中,同弧或等弧所对的圆周角相等.
14.1
15..
16.②
17.
18.任务一:弓形所在圆的半径为米;任务二:略;任务三:此时弓形所在圆的半径调整为米.
19.(1)等腰三角形三线合一;直径所对的圆周角是直角;(2)略;(3)答案不唯一.
20.(1)(2)3(3)最大值为,(4)的最小值为最大值为
21.约
22.
23.(1)略
(2)的半径为5.
24.略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.1圆的有关性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,内接于,是直径.若,则直径的长为( )
A.15 B. C.12 D.
2.如图,AB是⊙O的真径,点C、D在⊙O上,若∠ABD=50°.则∠BCD的度数为( )
A.25° B.30° C.35° D.40°
3.如图,是的两条弦,于点D,于点E,连结,.若,则的度数为( )
A. B. C. D.
4.如图,中,弦与交于点,点为中点,,,则的度数是( )
A. B. C. D.
5.如图,是四边形的外接圆的直径,点E 在上,连接,若,则 的度数为( )
A. B. C. D.
6.下列表述不正确的有( )
①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④半圆是弧;⑤圆内接四边形对角互补.
A.1个
B.2个
C.3个
D.4个
7.如图,点A,B,C在上,,则的度数是( )
A. B. C. D.
8.有下列说法:①弦是直径 ②半圆是弧 ③圆中最长的弦是直径 ④半圆是圆中最长的弧 ⑤平分弦的直径垂直于弦,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
9.下列命题中,正确的是( )
①顶点在圆心的角是圆心角;②相等的圆心角,所对的弧也相等;③两条弦相等,它们所对的弧也相等;④在等圆中,圆心角不等,所对的弦也不等.
A.①和② B.①和③
C.①和④ D.①、②、③、④
10.如图,是的直径,,是上的两点,且,则的度数为( )
A.42° B.84° C.90° D.96°
11.如图,AB是的直径,C、D是圆上两点,连接AC,AD,CD.若∠CAB=35°,则∠ADC的度数为( )
A.55° B.45° C.35° D.25°
12.如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A.OM的长 B.OM的长 C.2OM的长 D.CD的长
二、填空题
13.如图,ABC是⊙O的内接三角形,OD⊥BC于点D.下面是借助直尺,画出ABC中∠BAC的平分线的步骤:
①延长OD交于点M;
②连接AM交BC于点N.
所以∠BAN=∠CAN.
即线段AN为所求ABC中∠BAC的平分线.
请回答,得到∠BAN=∠CAN的依据是 .
14.如图,是圆O的直径,点C、D是半圆的三等分点,与交于点E.如果,那么 .
15.如图,已知正方形ABCD的各个顶点A、B、C、D都在⊙O上,如果P是的中点,PD与AB交于E点,那么= .
16.在同圆中,若AB和CD都是劣弧,且,那么成立的是 (填序号).
① ② ③ ④不确定
17.如图,内接于,,是的中点,且,分别是边上的高,则的大小 度.
三、解答题
18.根据以下素材,探索完成任务.
如何确定隧道的限高?
素材1 从小清家到附近山区的一条双行线公路上有一个隧道,在隧道口有一个限高标志(如图1),表示禁止装载高度(车顶最高处到地面)超过的车辆通行.那么这个限高是如何确定的呢?
素材2 小清通过实地调查和查阅相关资料,获得以下信息: ①隧道的横截面成轴对称,由一个矩形和一个弓形构成. ②隧道内的总宽度为,双行车道宽度为,隧道圆拱内壁最高处距路面,矩形的高为,车道两侧的人行道宽. ③为了保证安全,交通部门要求行驶车辆的顶部(设为平顶)与隧道圆拱内壁在竖直方向上的高度差相差最少.
问题解决
任务1 计算半径 求图1中弓形所在圆的半径.
任务2 确定限高 如图2,在安全的条件下,的限高是如何确定的?请通过计算说明理由.(参考数据:,结果保留一位小数)
任务3 尝试设计 如果要使高度不超过,宽为的货车能顺利通过这个隧道,且不改变隧道内的总宽度()和矩形的高(),如何设计隧道的弓形部分(求弓形所在圆的半径至少为多少米?)(参考数据:,结果保留一位小数)
19.阅读与思考
如图是小亮同学的数学日记,请仔细阅读,并完成相应的任务,
×年×月×日星期日
只用尺规也能判断两条线是否垂直
如图1,点是直线MN上一点,为射线,现在需要判断和是否垂直,然而我手头只有直尺和圆规,该怎么办呢?
我发现在初中三年的学习中很多知识都和直角有关,经过思考我想到了以下三个办法:
办法一:如图2,在射线上任取一点A,以A为圆心,大于长为半径作弧交于点B,点C,连接,若则,即.
办法二:如图3,在,上分别取点A,B,以AB为直径画圆,若点O在圆上,则.
办法三:如图4,在上任取一点A,以为边在作等边,延长交于点C,若,则,即.
还有只用尺规就可以判断和是否垂直的办法吗?……
任务:
(1)填空:“办法一”依据的数学定理是 ;“办法二”依据的数学定理是 ;
(2)请说明“办法三”尺规作图的合理性;
(3)在下图中再设计一种不同的方法探究与是否互相垂直(要求:尺规作图,保留作痕迹并描述探究的方法)
20.[发现问题]爱好数学的小明在做作业时碰到这样的一道题目∶
如图①,点O为坐标原点,的半径为1,点.动点B在上,连结,作等边(A,B,C 为顺时针顺序),求的最大值.
[解决问题]小明经过多次的尝试与探索,终于得到解题思路∶在图①中,连接,以为边在的左侧作等边三角形,连接.
(1)请你找出图中与相等的线段,并说明理由;
(2)线段的最大值为 .
[灵活运用]
(3)如图②,在平面直角坐标系中,点A的坐标为,点B的坐标为,点P为线段外一动点,且,以P为旋转中心,把逆时针旋转得,连接,求长的最大值及此时点P的坐标.
[迁移拓展]
(4)如图③,,点D是以为直径的半圆上不同于B、C的一个动点,以为边作等边,请直接写出的最值.
21.一辆卡车装满货物后,它的高比宽多,且恰好通过如图所示的隧道(上部为半圆形).卡车有多高?(结果精确到)
22.如图,圆环的内外圈用铁丝围成,其中大圆半径比小圆半径的2倍多1米,如果圆环的面积等于平方米,求围成圆环铁丝的总长度.
23.如图,是三角形的外接圆,是的直径,于点E.
(1)求证:;
(2)若长为8,,求的半径长.
24.已知如图,内接于,为直径,于点D,于点F.
(1)求证:;
(2)当点C是的中点时,求证:.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C C C C B C B
题号 11 12
答案 A B
1.B
2.D
3.B
4.C
5.C
6.C
7.C
8.B
9.C
10.B
11.A
12.B
13.在同圆或等圆中,同弧或等弧所对的圆周角相等.
14.1
15..
16.②
17.
18.任务一:弓形所在圆的半径为米;任务二:略;任务三:此时弓形所在圆的半径调整为米.
19.(1)等腰三角形三线合一;直径所对的圆周角是直角;(2)略;(3)答案不唯一.
20.(1)(2)3(3)最大值为,(4)的最小值为最大值为
21.约
22.
23.(1)略
(2)的半径为5.
24.略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
