24.2点和圆、直线和圆的位置关系同步练习(含答案)
文档属性
| 名称 | 24.2点和圆、直线和圆的位置关系同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 903.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 12:42:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.2点和圆、直线和圆的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,中,的长分别为.则可以用含的式子表示出的内切圆直径,下列表达式错误的是( )
A. B.
C. D.
2.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有两条边对应相等的两个直角三角形全等
C.垂直于圆的半径的直线是切线
D.对角线相等的平行四边形是矩形
3.已知⊙O1和⊙O2的半径分别为2和5,如果两圆的位置关系为外离,那么圆心距O1O2的取值范围在数轴上表示正确的是( )
A. B. C. D.
4.如图,点是直径的延长线上一点,切于点,已知,.则等于( )
A.2 B.3 C.4 D.5
5.若正三角形的外接圆半径为2,则它的内切圆半径为( )
A. B. C.2 D.1
6.如图,与相切于点A,交于点C,点D在上,且,若,,则的长为( )
A.3 B. C. D.4
7.在RtABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的半径是( )
A.10 B.5 C.4 D.3
8.如图,P是半径为6的⊙O外一点,且PO=12,过P点作⊙O的两条切线PA、PB,切点分别为点A、B,图中阴影部分的面积是( )
A.24π B.18π C.12π D.6π
9.如图,是⊙的直径,是⊙的切线,连接交⊙于点,连接,若,则的长为( )
A. B. C. D.
10.如图,PA,PB分别与⊙O相切于A,B两点,PA=AB,则∠AOB=( ).
A.100° B.110° C.120° D.130°
11.在平面直角坐标系中,以点为圆心,3为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相切,与y轴相离 D.与x轴相离,与y轴相交
12.如图,等腰内接于,直线是的切线,点C是切点,是半径,若,则的度数为( )
A. B. C. D.
二、填空题
13.的半径为,若圆心O到直线l的距离是,则直线l与的位置关系是 .
14.如图,与相切,切点为A,交于点C,点B是优弧上一点,若,则的度数为 .
15.在中,,,.以点为圆心,为半径的圆作⊙C,若边与⊙C只有一个公共点,则半径r的取值范围为 .
16.如图,在矩形中,是边上的点,经过三点的与相切于点.若,,则的半径是 .
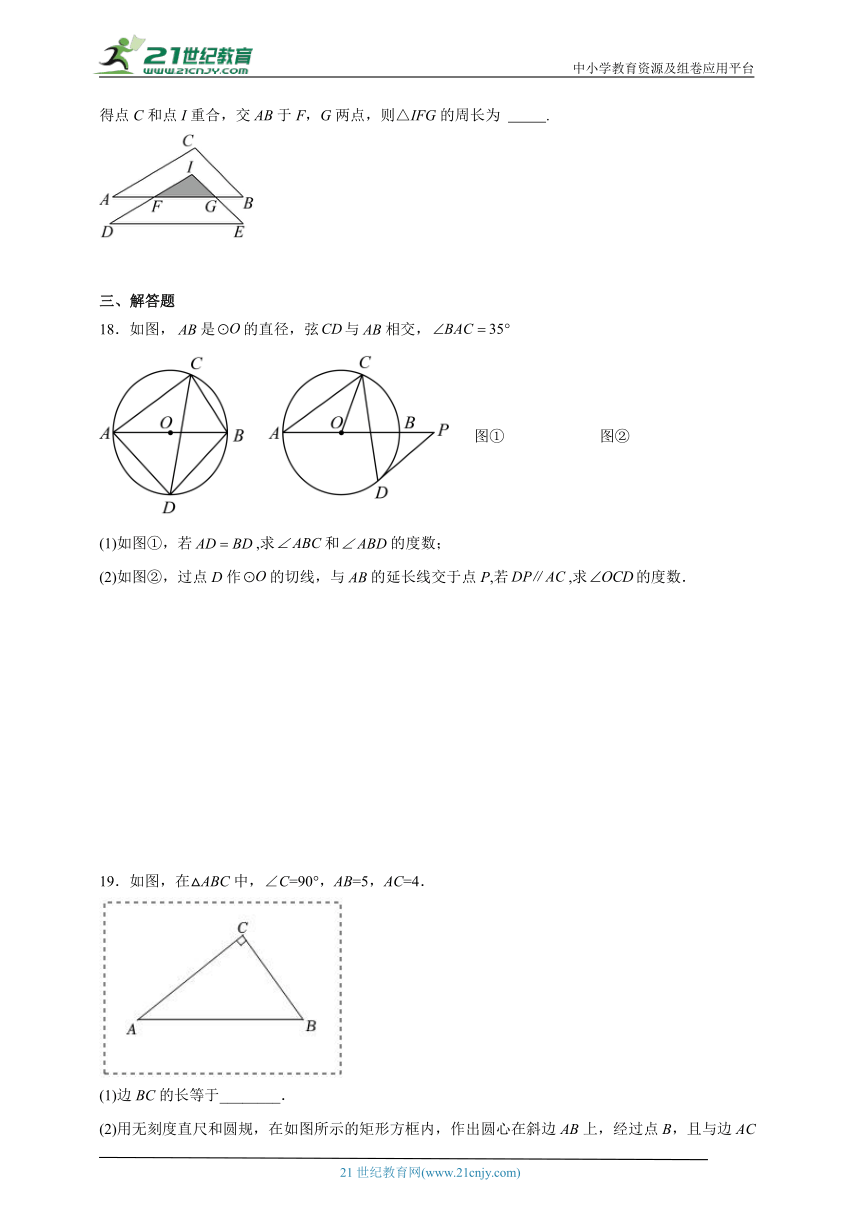
17.已知△ABC中,AB=7,AC=6,BC=5,I是△ABC的内心,把△ABC向下平移得到△IDE,使得点C和点I重合,交AB于F,G两点,则△IFG的周长为 .
三、解答题
18.如图,是的直径,弦与相交,
图① 图②
(1)如图①,若,求和的度数;
(2)如图②,过点D作的切线,与的延长线交于点P,若,求的度数.
19.如图,在△ABC中,∠C=90°,AB=5,AC=4.
(1)边BC的长等于________.
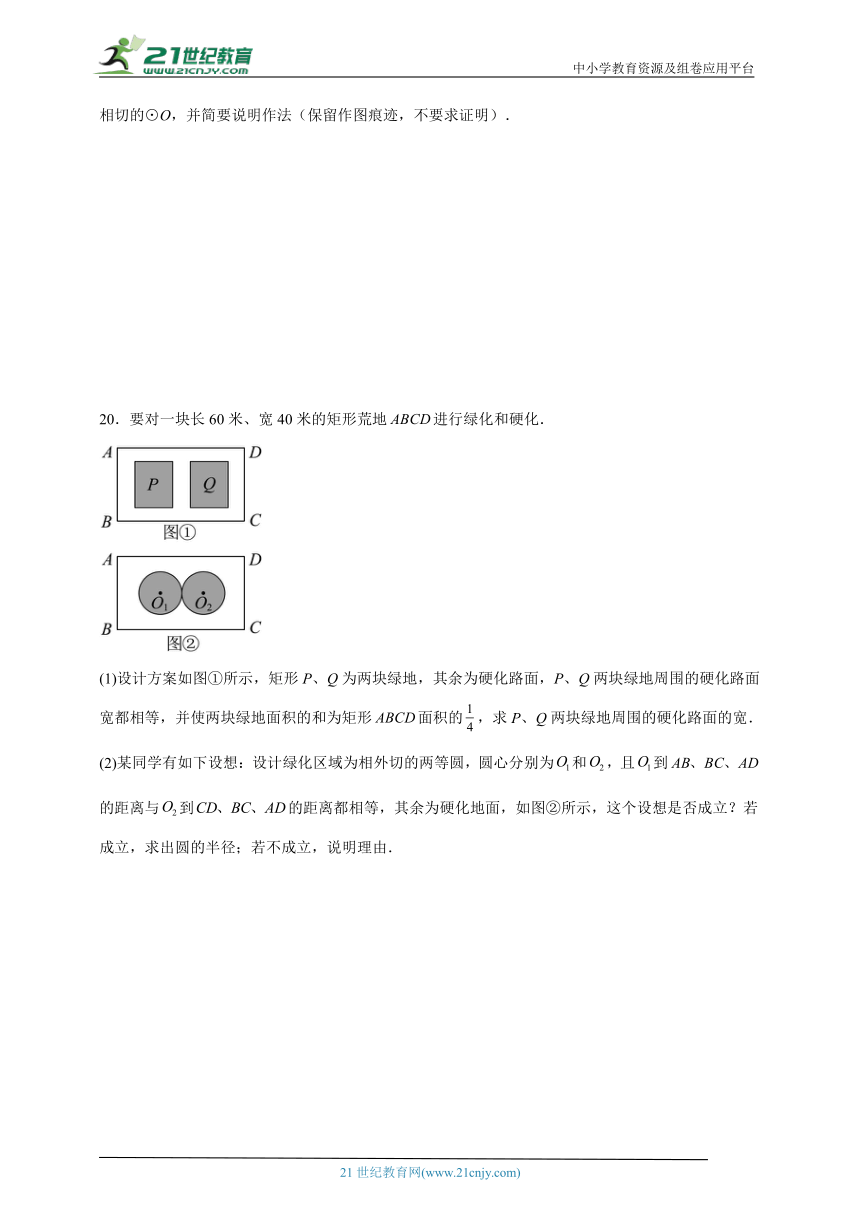
(2)用无刻度直尺和圆规,在如图所示的矩形方框内,作出圆心在斜边AB上,经过点B,且与边AC相切的⊙O,并简要说明作法(保留作图痕迹,不要求证明).
20.要对一块长60米、宽40米的矩形荒地进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形面积的,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为和,且到的距离与到的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
21.阅读理解:
(1)【学习心得】
小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.这类题目主要是两种类型.
①类型一,“定点+定长”:如图1,在中,是外一点,且,求的度数.
解:若以点(定点)为圆心,(定长)为半径作辅助圆,(请你在图1上画圆)则点必在上,是的圆心角,而是圆周角,从而可容易得到 .
②类型二,“定角+定弦”:如图,中,是内部的一个动点,且满足,求线段长的最小值.
解:,
,
,(定角)
点在以(定弦)为直径的上,请完成后面的过程.
(2)【问题解决】
如图3,在矩形中,已知,点是边上一动点(点不与,重合),连接,作点关于直线的对称点,则线段的最小值为 .
(3)【问题拓展】
如图4,在正方形中,,动点分别在边上移动,且满足.连接和,交于点.
①请你写出与的数量关系和位置关系,并说明理由;
②点从点开始运动到点时,点也随之运动,请求出点的运动路径长.
22.综合与实践【数学理解】德国数学家米勒曾提出最大视角问题,对该问题的一般描述是:如图2,已知点,是的边上的两个定点,是边上的一个动点,当且仅当的外接圆与边相切于点时,最大.人们称这一命题为米勒定理.
(1)【问题提出】如图1,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点,仅从射门角度大小考虑,甲是自己射门好,还是迅速将球回传给乙,让乙射门好?假设球员对球门的视角越大,足球越容易被踢进.请结合你所学知识,求证:.
(2)【问题解决】如图3,已知点,的坐标分别是,,是轴正半轴上的一动点,当的外接圆⊙与轴相切于点时,最大.当最大时,求点的坐标.
23.如图1,AB是的直径,点F是上的一点,连接AF,过点O作交于点C,过点C作的切线,交FA的延长线于点D,于E,连接AC.
(1)求证:;
(2)如图2,在图1的条件下,若点F为半圆的中点,连接CF交AB于点M,求的度数.
24.如图,为的直径,点C在上,点D为线段的延长线上一点,连接,过点O作交延长线于点E,交于点F,且满足.
(1)求证:是的切线;
(2)若,,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C C D C B C D C
题号 11 12
答案 B B
1.D
2.D
3.C
4.C
5.D
6.C
7.B
8.C
9.D
10.C
11.B
12.B
13.相交
14./38度
15.或
16.
17.7
18.(1),
(2)
19.(1)3
(2)略
20.(1)10米
(2)设想成立,10米
21.(1),
(2)2
(3),
22.(1)略
(2)
23.(1)
(2)
24.(1)略;(2)6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.2点和圆、直线和圆的位置关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,中,的长分别为.则可以用含的式子表示出的内切圆直径,下列表达式错误的是( )
A. B.
C. D.
2.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有两条边对应相等的两个直角三角形全等
C.垂直于圆的半径的直线是切线
D.对角线相等的平行四边形是矩形
3.已知⊙O1和⊙O2的半径分别为2和5,如果两圆的位置关系为外离,那么圆心距O1O2的取值范围在数轴上表示正确的是( )
A. B. C. D.
4.如图,点是直径的延长线上一点,切于点,已知,.则等于( )
A.2 B.3 C.4 D.5
5.若正三角形的外接圆半径为2,则它的内切圆半径为( )
A. B. C.2 D.1
6.如图,与相切于点A,交于点C,点D在上,且,若,,则的长为( )
A.3 B. C. D.4
7.在RtABC中,∠C=90°,AC=6,BC=8,则这个三角形的外接圆的半径是( )
A.10 B.5 C.4 D.3
8.如图,P是半径为6的⊙O外一点,且PO=12,过P点作⊙O的两条切线PA、PB,切点分别为点A、B,图中阴影部分的面积是( )
A.24π B.18π C.12π D.6π
9.如图,是⊙的直径,是⊙的切线,连接交⊙于点,连接,若,则的长为( )
A. B. C. D.
10.如图,PA,PB分别与⊙O相切于A,B两点,PA=AB,则∠AOB=( ).
A.100° B.110° C.120° D.130°
11.在平面直角坐标系中,以点为圆心,3为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相切,与y轴相离 D.与x轴相离,与y轴相交
12.如图,等腰内接于,直线是的切线,点C是切点,是半径,若,则的度数为( )
A. B. C. D.
二、填空题
13.的半径为,若圆心O到直线l的距离是,则直线l与的位置关系是 .
14.如图,与相切,切点为A,交于点C,点B是优弧上一点,若,则的度数为 .
15.在中,,,.以点为圆心,为半径的圆作⊙C,若边与⊙C只有一个公共点,则半径r的取值范围为 .
16.如图,在矩形中,是边上的点,经过三点的与相切于点.若,,则的半径是 .
17.已知△ABC中,AB=7,AC=6,BC=5,I是△ABC的内心,把△ABC向下平移得到△IDE,使得点C和点I重合,交AB于F,G两点,则△IFG的周长为 .
三、解答题
18.如图,是的直径,弦与相交,
图① 图②
(1)如图①,若,求和的度数;
(2)如图②,过点D作的切线,与的延长线交于点P,若,求的度数.
19.如图,在△ABC中,∠C=90°,AB=5,AC=4.
(1)边BC的长等于________.
(2)用无刻度直尺和圆规,在如图所示的矩形方框内,作出圆心在斜边AB上,经过点B,且与边AC相切的⊙O,并简要说明作法(保留作图痕迹,不要求证明).
20.要对一块长60米、宽40米的矩形荒地进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形面积的,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为和,且到的距离与到的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
21.阅读理解:
(1)【学习心得】
小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.这类题目主要是两种类型.
①类型一,“定点+定长”:如图1,在中,是外一点,且,求的度数.
解:若以点(定点)为圆心,(定长)为半径作辅助圆,(请你在图1上画圆)则点必在上,是的圆心角,而是圆周角,从而可容易得到 .
②类型二,“定角+定弦”:如图,中,是内部的一个动点,且满足,求线段长的最小值.
解:,
,
,(定角)
点在以(定弦)为直径的上,请完成后面的过程.
(2)【问题解决】
如图3,在矩形中,已知,点是边上一动点(点不与,重合),连接,作点关于直线的对称点,则线段的最小值为 .
(3)【问题拓展】
如图4,在正方形中,,动点分别在边上移动,且满足.连接和,交于点.
①请你写出与的数量关系和位置关系,并说明理由;
②点从点开始运动到点时,点也随之运动,请求出点的运动路径长.
22.综合与实践【数学理解】德国数学家米勒曾提出最大视角问题,对该问题的一般描述是:如图2,已知点,是的边上的两个定点,是边上的一个动点,当且仅当的外接圆与边相切于点时,最大.人们称这一命题为米勒定理.
(1)【问题提出】如图1,在足球比赛场上,甲、乙两名队员互相配合向对方球门进攻,当甲带球冲到点时,乙已跟随冲到点,仅从射门角度大小考虑,甲是自己射门好,还是迅速将球回传给乙,让乙射门好?假设球员对球门的视角越大,足球越容易被踢进.请结合你所学知识,求证:.
(2)【问题解决】如图3,已知点,的坐标分别是,,是轴正半轴上的一动点,当的外接圆⊙与轴相切于点时,最大.当最大时,求点的坐标.
23.如图1,AB是的直径,点F是上的一点,连接AF,过点O作交于点C,过点C作的切线,交FA的延长线于点D,于E,连接AC.
(1)求证:;
(2)如图2,在图1的条件下,若点F为半圆的中点,连接CF交AB于点M,求的度数.
24.如图,为的直径,点C在上,点D为线段的延长线上一点,连接,过点O作交延长线于点E,交于点F,且满足.
(1)求证:是的切线;
(2)若,,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C C D C B C D C
题号 11 12
答案 B B
1.D
2.D
3.C
4.C
5.D
6.C
7.B
8.C
9.D
10.C
11.B
12.B
13.相交
14./38度
15.或
16.
17.7
18.(1),
(2)
19.(1)3
(2)略
20.(1)10米
(2)设想成立,10米
21.(1),
(2)2
(3),
22.(1)略
(2)
23.(1)
(2)
24.(1)略;(2)6
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
