24.4弧长和扇形面积同步练习(含答案)
文档属性
| 名称 | 24.4弧长和扇形面积同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 809.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 12:44:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.4弧长和扇形面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个圆锥的侧面积是底面积的2倍,则圆锥的侧面积展开图的扇形圆心角度数为( )
A. B. C. D.
2.如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧、是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
A.4π+2 B. C. D.4π
3.已知圆锥的底面半径为3cm,母线长为5cm,那么它的侧面积是( )
A.12πcm2 B.15πcm2 C.20πcm2 D.30πcm2
4.今年寒假期间,小明参观了中国扇博物馆,如图是她看到的纸扇和团扇. 已知纸扇的骨柄长为30cm,扇面有纸部分的宽度为18cm,折扇张开的角度为150°,若这两把扇子的扇面面积相等,则团扇的半径为 ( )
A. B. C. D.
5.如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径,扇形圆心解,则该圆锥母线长为( )
A.10 B. C.6 D.8
6.如图所示,以长方形的各边为直径向外作半圆得到一个新的图形其周长为,同时此图形中四个半圆面积之和为,则长方形的面积为( )
A.10 B.20 C.40 D.80
7.如图,已知RtΔABC中,∠ACB=90°,AC= 4,BC=3,以AB边所在的直线为轴,将ΔABC旋转一周,则所得几何体的表面积是( ).
A. B. C. D.
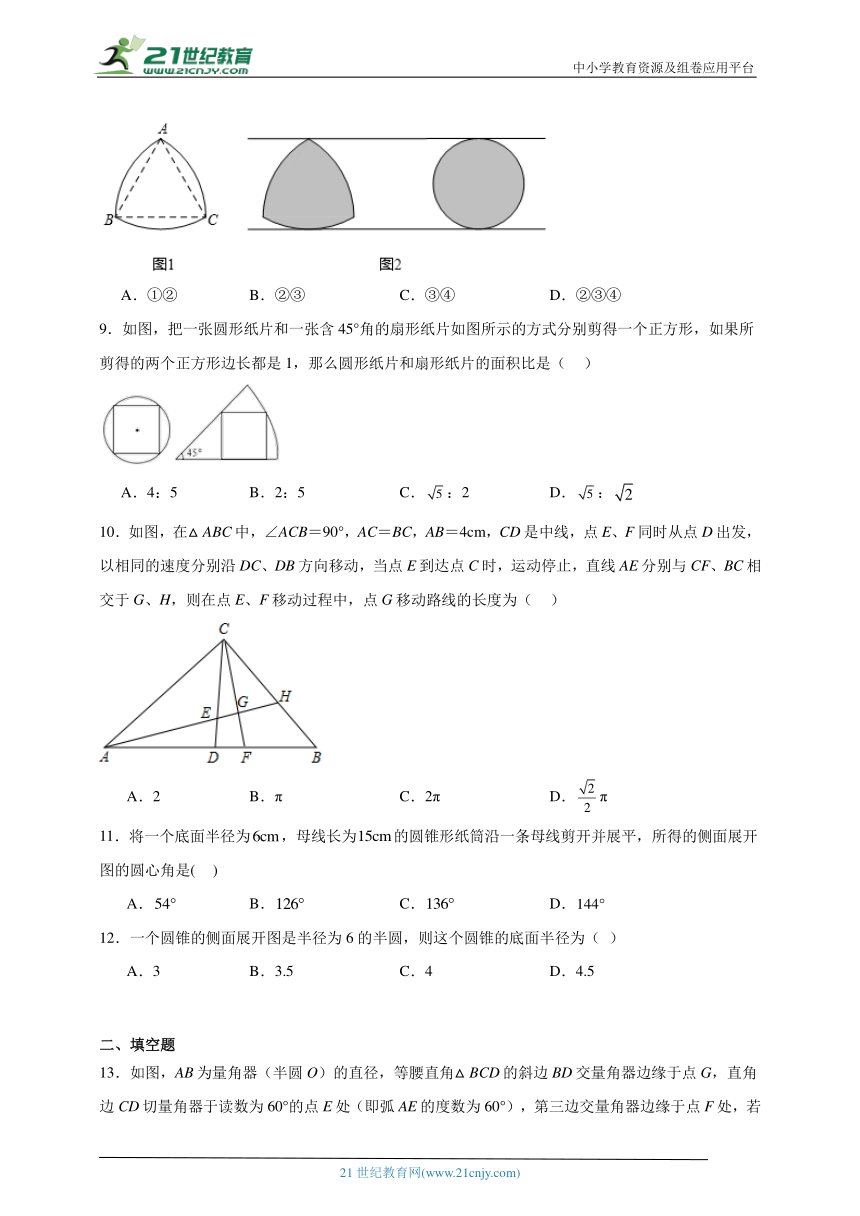
8.我们研究过的图形中,圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了圆以外,还有一些几何图形也是“等宽曲线”,如勒洛三角形(如图1),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆形滚木的截面图.有如下四个结论:
①勒洛三角形是中心对称图形;
②在图1中,等边三角形的边长为2,则勒洛三角形的周长为;
③在图2中,勒洛三角形的周长与圆的周长相等;
④使用截面是勒洛三角形的滚木来搬运东西,不会发生上下抖动;
上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.③④ D.②③④
9.如图,把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5 B.2:5 C.:2 D.:
10.如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点E、F移动过程中,点G移动路线的长度为( )
A.2 B.π C.2π D.π
11.将一个底面半径为,母线长为的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是( )
A. B. C. D.
12.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.3 B.3.5 C.4 D.4.5
二、填空题
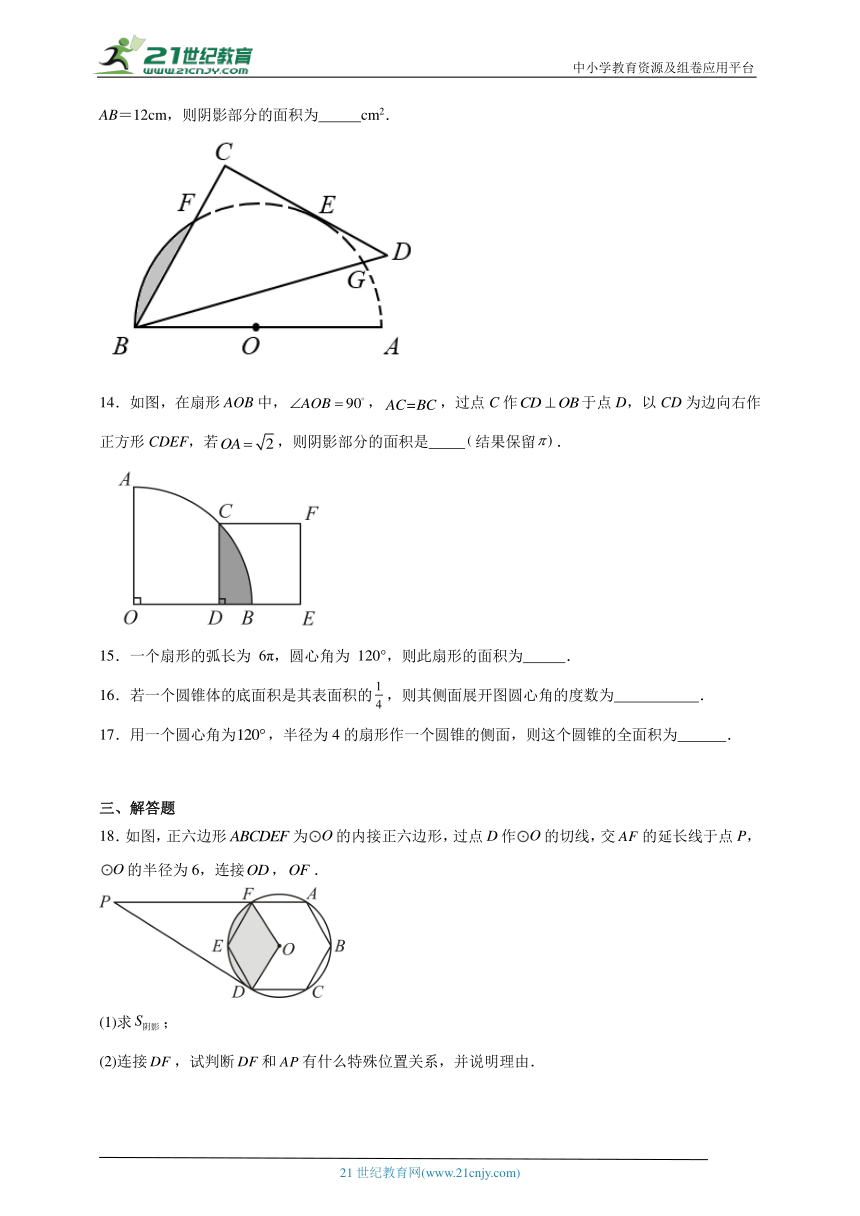
13.如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处,若AB=12cm,则阴影部分的面积为 cm2.
14.如图,在扇形AOB中,,,过点C作于点D,以CD为边向右作正方形CDEF,若,则阴影部分的面积是 结果保留.
15.一个扇形的弧长为 6π,圆心角为 120°,则此扇形的面积为 .
16.若一个圆锥体的底面积是其表面积的,则其侧面展开图圆心角的度数为 .
17.用一个圆心角为,半径为4的扇形作一个圆锥的侧面,则这个圆锥的全面积为 .
三、解答题
18.如图,正六边形为的内接正六边形,过点D作的切线,交的延长线于点P,的半径为6,连接,.
(1)求;
(2)连接,试判断和有什么特殊位置关系,并说明理由.
19.如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
20.如图:在平面直角坐标系中,网格中每个小正方形的边长为单位1.已知:
(1)与关于原点O对称,画出,并写出各顶点的坐标;
(2)以O为旋转中心将顺时针旋转得,画出,并写出各顶点的坐标;
(3)点C旋转到点经过的路线长为___________.
21.铅球比赛要求运动员在一固定圆圈内投掷,推出的铅球必须落在角的扇形区域内(以投掷圈的中心为圆心),这一区域为危险区域.如果运动员最多可投,那么这一比赛的危险区域的面积至少应是多少?(结果精确到)
22.龙舞腾盛世,某学校为传承中华传统龙狮文化,开办了龙狮特色基地.如图,在训练中,龙的尾部由四名同学摆成了一个弧形,这弧形的弧长部分占龙总长的二分之一,已知弧形的半径为2米,圆心角为,求整条龙的长.
23.如图,已知是的直径,切于点,过作直线交于另一点,连接、.
(1)求证:平分;
(2)若是直径上方半圆弧上一动点,的半径为2,则
①当弦的长是 时,以,,,为顶点的四边形是正方形;
②当的长度是 时,以,,,为顶点的四边形是菱形.
24.如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=100°,∠DBC=80°.
(1)求证:BD=CD;
(2)若圆O的半径为9,求的长(结果保留π).
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B D C C C D A D
题号 11 12
答案 D A
1.B
2.A
3.B
4.D
5.C
6.C
7.C
8.D
9.A
10.D
11.D
12.A
13.
14.
15.27π
16.120°/120度
17.
18.(1)
(2)
19.72πm2.
20.(1)、、
(2)、、
(3)
21.约
22.米
23.(1)略;(2)①;②或.
24.(1)略(2) 2π
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.4弧长和扇形面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个圆锥的侧面积是底面积的2倍,则圆锥的侧面积展开图的扇形圆心角度数为( )
A. B. C. D.
2.如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧、是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
A.4π+2 B. C. D.4π
3.已知圆锥的底面半径为3cm,母线长为5cm,那么它的侧面积是( )
A.12πcm2 B.15πcm2 C.20πcm2 D.30πcm2
4.今年寒假期间,小明参观了中国扇博物馆,如图是她看到的纸扇和团扇. 已知纸扇的骨柄长为30cm,扇面有纸部分的宽度为18cm,折扇张开的角度为150°,若这两把扇子的扇面面积相等,则团扇的半径为 ( )
A. B. C. D.
5.如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径,扇形圆心解,则该圆锥母线长为( )
A.10 B. C.6 D.8
6.如图所示,以长方形的各边为直径向外作半圆得到一个新的图形其周长为,同时此图形中四个半圆面积之和为,则长方形的面积为( )
A.10 B.20 C.40 D.80
7.如图,已知RtΔABC中,∠ACB=90°,AC= 4,BC=3,以AB边所在的直线为轴,将ΔABC旋转一周,则所得几何体的表面积是( ).
A. B. C. D.
8.我们研究过的图形中,圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了圆以外,还有一些几何图形也是“等宽曲线”,如勒洛三角形(如图1),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆形滚木的截面图.有如下四个结论:
①勒洛三角形是中心对称图形;
②在图1中,等边三角形的边长为2,则勒洛三角形的周长为;
③在图2中,勒洛三角形的周长与圆的周长相等;
④使用截面是勒洛三角形的滚木来搬运东西,不会发生上下抖动;
上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.③④ D.②③④
9.如图,把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
A.4:5 B.2:5 C.:2 D.:
10.如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点E、F移动过程中,点G移动路线的长度为( )
A.2 B.π C.2π D.π
11.将一个底面半径为,母线长为的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是( )
A. B. C. D.
12.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A.3 B.3.5 C.4 D.4.5
二、填空题
13.如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处,若AB=12cm,则阴影部分的面积为 cm2.
14.如图,在扇形AOB中,,,过点C作于点D,以CD为边向右作正方形CDEF,若,则阴影部分的面积是 结果保留.
15.一个扇形的弧长为 6π,圆心角为 120°,则此扇形的面积为 .
16.若一个圆锥体的底面积是其表面积的,则其侧面展开图圆心角的度数为 .
17.用一个圆心角为,半径为4的扇形作一个圆锥的侧面,则这个圆锥的全面积为 .
三、解答题
18.如图,正六边形为的内接正六边形,过点D作的切线,交的延长线于点P,的半径为6,连接,.
(1)求;
(2)连接,试判断和有什么特殊位置关系,并说明理由.
19.如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
20.如图:在平面直角坐标系中,网格中每个小正方形的边长为单位1.已知:
(1)与关于原点O对称,画出,并写出各顶点的坐标;
(2)以O为旋转中心将顺时针旋转得,画出,并写出各顶点的坐标;
(3)点C旋转到点经过的路线长为___________.
21.铅球比赛要求运动员在一固定圆圈内投掷,推出的铅球必须落在角的扇形区域内(以投掷圈的中心为圆心),这一区域为危险区域.如果运动员最多可投,那么这一比赛的危险区域的面积至少应是多少?(结果精确到)
22.龙舞腾盛世,某学校为传承中华传统龙狮文化,开办了龙狮特色基地.如图,在训练中,龙的尾部由四名同学摆成了一个弧形,这弧形的弧长部分占龙总长的二分之一,已知弧形的半径为2米,圆心角为,求整条龙的长.
23.如图,已知是的直径,切于点,过作直线交于另一点,连接、.
(1)求证:平分;
(2)若是直径上方半圆弧上一动点,的半径为2,则
①当弦的长是 时,以,,,为顶点的四边形是正方形;
②当的长度是 时,以,,,为顶点的四边形是菱形.
24.如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=100°,∠DBC=80°.
(1)求证:BD=CD;
(2)若圆O的半径为9,求的长(结果保留π).
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B D C C C D A D
题号 11 12
答案 D A
1.B
2.A
3.B
4.D
5.C
6.C
7.C
8.D
9.A
10.D
11.D
12.A
13.
14.
15.27π
16.120°/120度
17.
18.(1)
(2)
19.72πm2.
20.(1)、、
(2)、、
(3)
21.约
22.米
23.(1)略;(2)①;②或.
24.(1)略(2) 2π
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
