21.2 解一元二次方程 同步练习(含答案)
文档属性
| 名称 | 21.2 解一元二次方程 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 458.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
21.2解一元二次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用配方法解方程,下面配方正确的是( )
A. B. C. D.
2.已知=1,则ax2+bx+c=0( )
A.无实根
B.有两个相等实根
C.有相异的两实根
D.有实根,但不能确定是否一定是相等两实根
3.已知两个关于x的一元二次方程,其中.下列结论错误的是( )
A.若方程M有两个相等的实数根,则方程N也有两个相等的实数根
B.若方程M有一个正根和一个负根,则方程N也有一个正根和一个负根
C.若5是方程M的一个根,则是方程N的一个根
D.若方程M和方程N有一个相同的根,则这个根一定是
4.已知m,n是一元二次方程x2﹣4x﹣3=0的两个实数根,则代数式(m+1)(n+1)的值为( )
A.﹣6 B.﹣2 C.0 D.2
5.一元二次方程x2+x+1=0根的情况为( )
A.没有实数根 B.有两个不等实数根
C.有两个相等实数根 D.无法判断
6.当m取下列哪个值时,关于x的一元二次方程x2﹣2x+m=0没有实数根( )
A.2 B.0 C.1 D.﹣2
7.用配方法解一元二次方程x2﹣4x﹣6=0时,配方后的方程是( )
A.(x+2)2=2 B.(x﹣2)2=2 C.(x+2)2=10 D.(x﹣2)2=10
8.若,则的值为( )
A. B. C.或 D.
9.方程 (x+)2+(x+)(2x-1)=0的较大根为( )
A.- B. C. D.
10.关于x的方程与.①若第一个方程,则第二个方程必有两个不相等的实数根,②若第一方程有两个正数解为 ,则第二个方程的解必,则下列判断正确的是( )
A.①错②对 B.①错②错 C.①对②错 D.①对②对
11.一个三角形的两边长分别等于一元二次方程的两个实数根,则下列说法正确的是( )
A.第三边的长可能是17 B.第三边的长可能是16
C.第三边的长可能为5 D.三角形的周长可能为21
12.把一元二次方程化为的形式正确的是( )
A. B. C. D.
二、填空题
13.关于x的一元二次方程x2-3x+m=0有实数根α、β,且α2+β2=17,则m的值是 .
14.设,是一元二次方程的两根,则 .
15.若关于的方程有两个不相等的实数根,则的取值范围是 .
16.已知实数a,b满足,,则=
17.若关于x的一元二次方程没有实数根,则a的取值范围是 .
三、解答题
18.解方程:
19.利用面积关系,研究方程,提出问题:怎样图解一元二次方程()?
几何建模:
(1)将原方程变形为:.
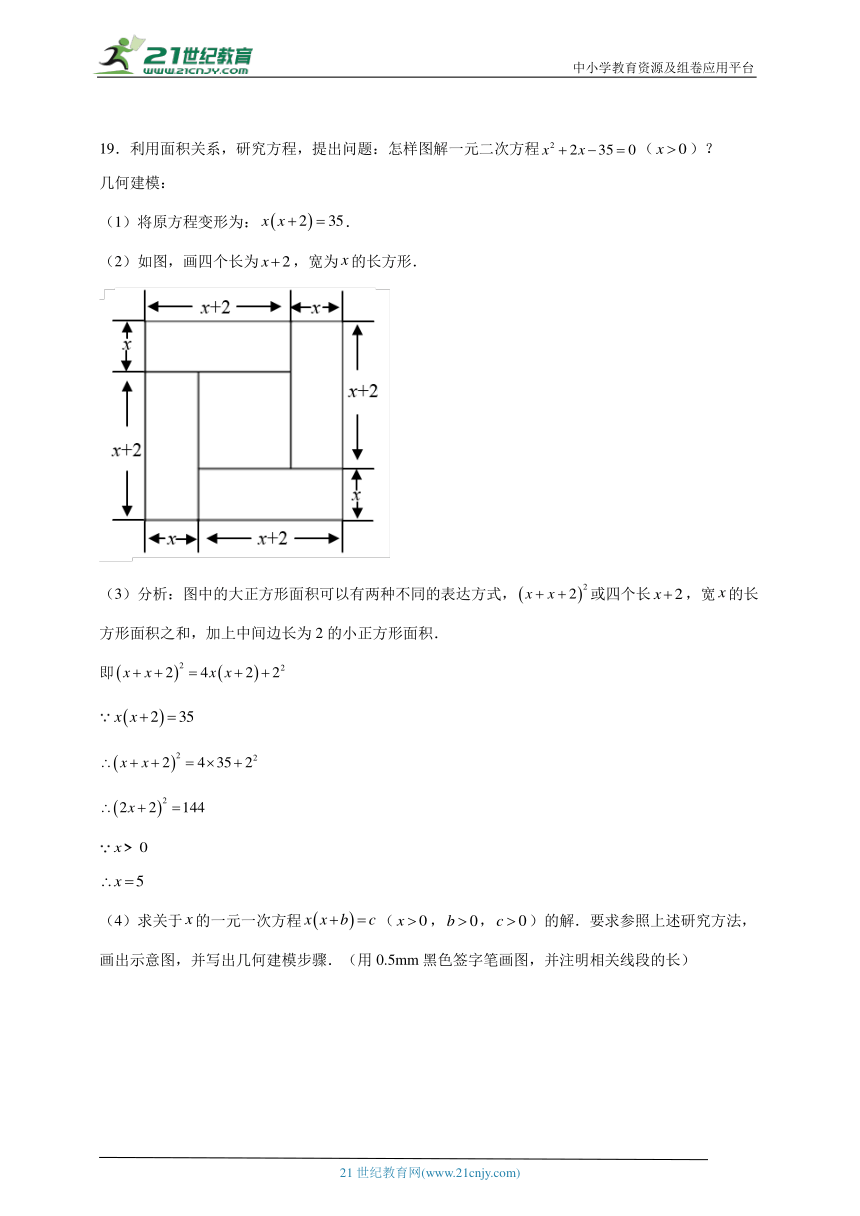
(2)如图,画四个长为,宽为的长方形.
(3)分析:图中的大正方形面积可以有两种不同的表达方式,或四个长,宽的长方形面积之和,加上中间边长为2的小正方形面积.
即
(4)求关于的一元一次方程(,,)的解.要求参照上述研究方法,画出示意图,并写出几何建模步骤.(用0.5mm黑色签字笔画图,并注明相关线段的长)
20.求证:对于任意实数,关于的方程总有两个不相等的实数根.
21.阅读理解:
材料1:若代数式在实数范围内可因式分解为.
令我们可以得到该方程的两个解为,,则我们也可以得到关于的方程的两个解也为,,那么我们称这两个解为“共生根”,由得到两个“共生根”与各项系数之间的关系为:,.
材料2:已知实数,满足,,且,根据材料1求的值.
解:由题知,是方程足的两个不相等的“共生根”,
根据材料1得:,,
.
解决以下问题:
(1)方程的两个“共生根”为,,则_______,_______;
(2)已知实数,满足,,且,求的值;
(3)已知实数,满足,,且,求.
22.某口罩厂计划在一定时间内生产240万个口罩,后因为防控需要,不但需要增产,而且要提前4天完成任务.经测算,每天需要多生产8万个口罩.问原计划每天生产多少万个口罩?
23.已知关于的方程.
(1)求证:无论取什么数,方程总有两个实数根;
(2)若已知方程有一个实数根是,试求出另一个实数根.
24.关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根为负数,求m的取值范围.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D A A D A B A
题号 11 12
答案 B A
1.B
2.D
3.D
4.D
5.A
6.A
7.D
8.A
9.B
10.A
11.B
12.A
13.-4
14.
15.
16.2022
17.
18.,.
19.(1);(2)略;(3).
20.略
21.(1),
(2)
(3)
22.原计划每天生产10万个口罩
23.(1)略
(2)方程的另一个实数根是
24.(1)略;(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
21.2解一元二次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用配方法解方程,下面配方正确的是( )
A. B. C. D.
2.已知=1,则ax2+bx+c=0( )
A.无实根
B.有两个相等实根
C.有相异的两实根
D.有实根,但不能确定是否一定是相等两实根
3.已知两个关于x的一元二次方程,其中.下列结论错误的是( )
A.若方程M有两个相等的实数根,则方程N也有两个相等的实数根
B.若方程M有一个正根和一个负根,则方程N也有一个正根和一个负根
C.若5是方程M的一个根,则是方程N的一个根
D.若方程M和方程N有一个相同的根,则这个根一定是
4.已知m,n是一元二次方程x2﹣4x﹣3=0的两个实数根,则代数式(m+1)(n+1)的值为( )
A.﹣6 B.﹣2 C.0 D.2
5.一元二次方程x2+x+1=0根的情况为( )
A.没有实数根 B.有两个不等实数根
C.有两个相等实数根 D.无法判断
6.当m取下列哪个值时,关于x的一元二次方程x2﹣2x+m=0没有实数根( )
A.2 B.0 C.1 D.﹣2
7.用配方法解一元二次方程x2﹣4x﹣6=0时,配方后的方程是( )
A.(x+2)2=2 B.(x﹣2)2=2 C.(x+2)2=10 D.(x﹣2)2=10
8.若,则的值为( )
A. B. C.或 D.
9.方程 (x+)2+(x+)(2x-1)=0的较大根为( )
A.- B. C. D.
10.关于x的方程与.①若第一个方程,则第二个方程必有两个不相等的实数根,②若第一方程有两个正数解为 ,则第二个方程的解必,则下列判断正确的是( )
A.①错②对 B.①错②错 C.①对②错 D.①对②对
11.一个三角形的两边长分别等于一元二次方程的两个实数根,则下列说法正确的是( )
A.第三边的长可能是17 B.第三边的长可能是16
C.第三边的长可能为5 D.三角形的周长可能为21
12.把一元二次方程化为的形式正确的是( )
A. B. C. D.
二、填空题
13.关于x的一元二次方程x2-3x+m=0有实数根α、β,且α2+β2=17,则m的值是 .
14.设,是一元二次方程的两根,则 .
15.若关于的方程有两个不相等的实数根,则的取值范围是 .
16.已知实数a,b满足,,则=
17.若关于x的一元二次方程没有实数根,则a的取值范围是 .
三、解答题
18.解方程:
19.利用面积关系,研究方程,提出问题:怎样图解一元二次方程()?
几何建模:
(1)将原方程变形为:.
(2)如图,画四个长为,宽为的长方形.
(3)分析:图中的大正方形面积可以有两种不同的表达方式,或四个长,宽的长方形面积之和,加上中间边长为2的小正方形面积.
即
(4)求关于的一元一次方程(,,)的解.要求参照上述研究方法,画出示意图,并写出几何建模步骤.(用0.5mm黑色签字笔画图,并注明相关线段的长)
20.求证:对于任意实数,关于的方程总有两个不相等的实数根.
21.阅读理解:
材料1:若代数式在实数范围内可因式分解为.
令我们可以得到该方程的两个解为,,则我们也可以得到关于的方程的两个解也为,,那么我们称这两个解为“共生根”,由得到两个“共生根”与各项系数之间的关系为:,.
材料2:已知实数,满足,,且,根据材料1求的值.
解:由题知,是方程足的两个不相等的“共生根”,
根据材料1得:,,
.
解决以下问题:
(1)方程的两个“共生根”为,,则_______,_______;
(2)已知实数,满足,,且,求的值;
(3)已知实数,满足,,且,求.
22.某口罩厂计划在一定时间内生产240万个口罩,后因为防控需要,不但需要增产,而且要提前4天完成任务.经测算,每天需要多生产8万个口罩.问原计划每天生产多少万个口罩?
23.已知关于的方程.
(1)求证:无论取什么数,方程总有两个实数根;
(2)若已知方程有一个实数根是,试求出另一个实数根.
24.关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根为负数,求m的取值范围.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D A A D A B A
题号 11 12
答案 B A
1.B
2.D
3.D
4.D
5.A
6.A
7.D
8.A
9.B
10.A
11.B
12.A
13.-4
14.
15.
16.2022
17.
18.,.
19.(1);(2)略;(3).
20.略
21.(1),
(2)
(3)
22.原计划每天生产10万个口罩
23.(1)略
(2)方程的另一个实数根是
24.(1)略;(2)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
