22.2二次函数与一元二次方程同步练习(含答案)
文档属性
| 名称 | 22.2二次函数与一元二次方程同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 636.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 12:46:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
22.2二次函数与一元二次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,抛物线与x轴交于点A,B,对称轴为直线,若点A的坐标为,则下列结论:①点B的坐标为;②;③;④点在抛物线上,当时,则,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
2.如图,顶点为的抛物线经过点,则下列结论中正确的是( )
A.
B.若点在抛物线上,则
C.当时,y随x的增大而减小
D.关于x的一元二次方程有两个不相等的实数根
3.下列抛物线中,过原点的抛物线是( )
A.y 4x 2 1 B.y 4x 2 1 C.y 4(x 1) 2 D.y 4x 2 x
4.无论为何值,直线与抛物线总有公共点,则的取值范围是( )
A. B. C.或 D.
5.二次函数y=mx2+x﹣2m(m是非0常数)的图象与x轴的交点个数为( )
A.0个 B.1个 C.2个 D.1个或2个
6.已知二次函数的图象如图所示,则下列结论:①方程的两根之和大于0; ;随的增大而增大;④,⑤2a-b>0. 其中正确的个数( )
A.4个 B.3个 C.2个 D.1个
7.已知二次函数的顶点为,那么关于的一元二次方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
8.如图是二次函数的部分图象,由图象可知不等式的解集是( )
A. B.
C. D.
9.已知二次函数(k为常数)的图象与x轴的一个交点是,则关于x的一元二次方程的两个实数根是( )
A., B.,
C., D.,
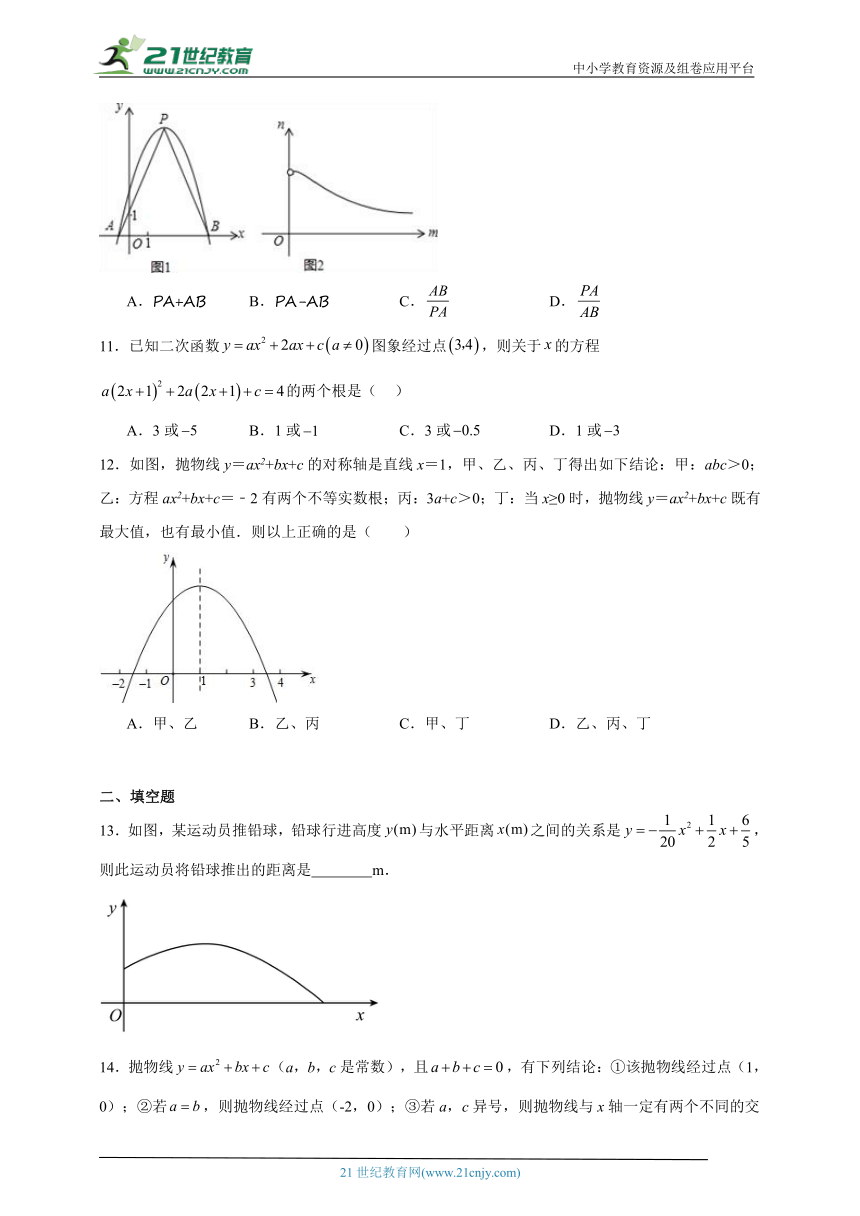
10.如图1,抛物线y=-x2+bx+c的顶点为P,与x轴交于A,B两点.若A,B两点间的距离为m,n是m的函数,且表示n与m的函数关系的图象大致如图2所示,则n可能为( )
A.PA+AB B.PA-AB C. D.
11.已知二次函数图象经过点,则关于的方程的两个根是( )
A.3或 B.1或 C.3或 D.1或
12.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,甲、乙、丙、丁得出如下结论:甲:abc>0;乙:方程ax2+bx+c=﹣2有两个不等实数根;丙:3a+c>0;丁:当x≥0时,抛物线y=ax2+bx+c既有最大值,也有最小值.则以上正确的是( )
A.甲、乙 B.乙、丙 C.甲、丁 D.乙、丙、丁
二、填空题
13.如图,某运动员推铅球,铅球行进高度与水平距离之间的关系是,则此运动员将铅球推出的距离是 m.
14.抛物线(a,b,c是常数),且,有下列结论:①该抛物线经过点(1,0);②若,则抛物线经过点(-2,0);③若a,c异号,则抛物线与x轴一定有两个不同的交点;④点在抛物线上,且,若,则.其中所有正确结论的序号是 .
15.如图,抛物线过点,且对称轴为直线,有下列结论:;;抛物线经过点与点,则;方程的一个解是;,其中所有正确的结论是 .
16.已知:二次函数中的x,y满足下表:
x … 0 1 2 3 …
y … 0 … …
根据上表,当时,x的取值范围为 .
17.抛物线的对称轴及部分图象如图所示,则关于x的一元二次方程的两根为 .
三、解答题
18.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x … -1 0 1 2 3 4 …
y … 8 3 0 -1 0 3 …
(1)求该二次函数的解析式;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+2,y2)两点都在该函数的图象上,计算当m 取何值时,?
19.定义:将二次函数在轴下方部分沿轴向上翻折,翻折后部分与原来末翻折部分形成一个新的函数,那么称函数为原二次函数的有趣函数.
(1)二次函数_______________(有/没有)有趣函数.
(2)已知二次函数与轴交于点(1,0),(5,0),与轴交于点,求拋物线的解析式,并在坐标系中画出函数图像.
(3)在(2)的条件下:
①过点作轴的平行线与抛物线交于点,求线段的长度.
②若函数为原二次函数的有趣函数,画出函数的图像并求解当函数的函数值大于2时,自变量的取值范围(直接写出答案).
20.在平面直角坐标系中,若点的横坐标和纵坐标相等或互为相反数,则称点为“美丽点”.例如点,,,…,都是“美丽点”.
(1)直接写出抛物线上的“美丽点”为 .
(2)若二次函数的图象上无“美丽点”,则的取值范围为 .
(3)已知二次函数的图象上只有三个“美丽点”,其中一个“美丽点”是,当时,函数的最小值为,最大值为,求的取值范围.
21.许多数学问题源于生活.如图①是撑开后的户外遮阳伞,可以发现数学研究的对象一抛物线.在如图②所示的直角坐标系中,伞柄在轴上,坐标原点为伞骨的交点.点为抛物线的顶点,点在抛物线上,关于轴对称.分米,点到轴的距离是2分米,两点之间的距离是12分米.
(1)求抛物线的解析式(不要求写自变量取值范围);
(2)如图③,分别延长交拋物线于点,请直接写出两点间距离的值;
(3)如图③,以拋物线与坐标轴的三个交点为顶点的三角形面积为,将拋物线向左平移个单位,得到一条新拋物线,以新抛物线与坐标轴的三个交点为顶点的三角形面积为.若,求的值.
22.利用二次函数的图象求一元二次方程的近似根.
23.已知二次函数的图象过点
(1)求证:;
(2)求证:此二次函数的图象与x轴必有两个交点;
(3)若二次函数的图象与x轴交于点、,,求b的值.
24.已知函数y=(m+)x2+(2m﹣1)x﹣3.求证:不论m为何值,该函数图象与x轴必有交点.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D C C B C D C C
题号 11 12
答案 D B
1.B
2.C
3.D
4.C
5.C
6.B
7.C
8.D
9.C
10.C
11.D
12.B
13.12
14.①②③
15.②⑤
16.x<-1或x>3
17.,
18.(1)y=x2-4x+3;(2)当x=2时,ymin=-1;(3)m<1.
19.(1)没有
(2)
(3)①6;②或或
20.(1)
(2)
(3)
21.(1)
(2)24分米
(3)或
22.,
23.(1)略;
(2)略;
(3),;
24.略.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.2二次函数与一元二次方程
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,抛物线与x轴交于点A,B,对称轴为直线,若点A的坐标为,则下列结论:①点B的坐标为;②;③;④点在抛物线上,当时,则,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
2.如图,顶点为的抛物线经过点,则下列结论中正确的是( )
A.
B.若点在抛物线上,则
C.当时,y随x的增大而减小
D.关于x的一元二次方程有两个不相等的实数根
3.下列抛物线中,过原点的抛物线是( )
A.y 4x 2 1 B.y 4x 2 1 C.y 4(x 1) 2 D.y 4x 2 x
4.无论为何值,直线与抛物线总有公共点,则的取值范围是( )
A. B. C.或 D.
5.二次函数y=mx2+x﹣2m(m是非0常数)的图象与x轴的交点个数为( )
A.0个 B.1个 C.2个 D.1个或2个
6.已知二次函数的图象如图所示,则下列结论:①方程的两根之和大于0; ;随的增大而增大;④,⑤2a-b>0. 其中正确的个数( )
A.4个 B.3个 C.2个 D.1个
7.已知二次函数的顶点为,那么关于的一元二次方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
8.如图是二次函数的部分图象,由图象可知不等式的解集是( )
A. B.
C. D.
9.已知二次函数(k为常数)的图象与x轴的一个交点是,则关于x的一元二次方程的两个实数根是( )
A., B.,
C., D.,
10.如图1,抛物线y=-x2+bx+c的顶点为P,与x轴交于A,B两点.若A,B两点间的距离为m,n是m的函数,且表示n与m的函数关系的图象大致如图2所示,则n可能为( )
A.PA+AB B.PA-AB C. D.
11.已知二次函数图象经过点,则关于的方程的两个根是( )
A.3或 B.1或 C.3或 D.1或
12.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,甲、乙、丙、丁得出如下结论:甲:abc>0;乙:方程ax2+bx+c=﹣2有两个不等实数根;丙:3a+c>0;丁:当x≥0时,抛物线y=ax2+bx+c既有最大值,也有最小值.则以上正确的是( )
A.甲、乙 B.乙、丙 C.甲、丁 D.乙、丙、丁
二、填空题
13.如图,某运动员推铅球,铅球行进高度与水平距离之间的关系是,则此运动员将铅球推出的距离是 m.
14.抛物线(a,b,c是常数),且,有下列结论:①该抛物线经过点(1,0);②若,则抛物线经过点(-2,0);③若a,c异号,则抛物线与x轴一定有两个不同的交点;④点在抛物线上,且,若,则.其中所有正确结论的序号是 .
15.如图,抛物线过点,且对称轴为直线,有下列结论:;;抛物线经过点与点,则;方程的一个解是;,其中所有正确的结论是 .
16.已知:二次函数中的x,y满足下表:
x … 0 1 2 3 …
y … 0 … …
根据上表,当时,x的取值范围为 .
17.抛物线的对称轴及部分图象如图所示,则关于x的一元二次方程的两根为 .
三、解答题
18.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
x … -1 0 1 2 3 4 …
y … 8 3 0 -1 0 3 …
(1)求该二次函数的解析式;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+2,y2)两点都在该函数的图象上,计算当m 取何值时,?
19.定义:将二次函数在轴下方部分沿轴向上翻折,翻折后部分与原来末翻折部分形成一个新的函数,那么称函数为原二次函数的有趣函数.
(1)二次函数_______________(有/没有)有趣函数.
(2)已知二次函数与轴交于点(1,0),(5,0),与轴交于点,求拋物线的解析式,并在坐标系中画出函数图像.
(3)在(2)的条件下:
①过点作轴的平行线与抛物线交于点,求线段的长度.
②若函数为原二次函数的有趣函数,画出函数的图像并求解当函数的函数值大于2时,自变量的取值范围(直接写出答案).
20.在平面直角坐标系中,若点的横坐标和纵坐标相等或互为相反数,则称点为“美丽点”.例如点,,,…,都是“美丽点”.
(1)直接写出抛物线上的“美丽点”为 .
(2)若二次函数的图象上无“美丽点”,则的取值范围为 .
(3)已知二次函数的图象上只有三个“美丽点”,其中一个“美丽点”是,当时,函数的最小值为,最大值为,求的取值范围.
21.许多数学问题源于生活.如图①是撑开后的户外遮阳伞,可以发现数学研究的对象一抛物线.在如图②所示的直角坐标系中,伞柄在轴上,坐标原点为伞骨的交点.点为抛物线的顶点,点在抛物线上,关于轴对称.分米,点到轴的距离是2分米,两点之间的距离是12分米.
(1)求抛物线的解析式(不要求写自变量取值范围);
(2)如图③,分别延长交拋物线于点,请直接写出两点间距离的值;
(3)如图③,以拋物线与坐标轴的三个交点为顶点的三角形面积为,将拋物线向左平移个单位,得到一条新拋物线,以新抛物线与坐标轴的三个交点为顶点的三角形面积为.若,求的值.
22.利用二次函数的图象求一元二次方程的近似根.
23.已知二次函数的图象过点
(1)求证:;
(2)求证:此二次函数的图象与x轴必有两个交点;
(3)若二次函数的图象与x轴交于点、,,求b的值.
24.已知函数y=(m+)x2+(2m﹣1)x﹣3.求证:不论m为何值,该函数图象与x轴必有交点.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D C C B C D C C
题号 11 12
答案 D B
1.B
2.C
3.D
4.C
5.C
6.B
7.C
8.D
9.C
10.C
11.D
12.B
13.12
14.①②③
15.②⑤
16.x<-1或x>3
17.,
18.(1)y=x2-4x+3;(2)当x=2时,ymin=-1;(3)m<1.
19.(1)没有
(2)
(3)①6;②或或
20.(1)
(2)
(3)
21.(1)
(2)24分米
(3)或
22.,
23.(1)略;
(2)略;
(3),;
24.略.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
