第二十三章旋转单元测试(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十三章旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2023年9月21日,“天宫课堂”第四课在中国空间站成功开讲,本次太空授课活动激发了广大青少年不断追寻“科学梦”,实现“航天梦”的热情.下列相关卡通图标分别是“星球”“宇航员”“星系”和“黑洞”,其中是中心对称图形的是( )
B.
C. D.
2.如图,在中,已知,,,若将绕点C时针方向旋转180 ,得到,则,的坐标依次是( )
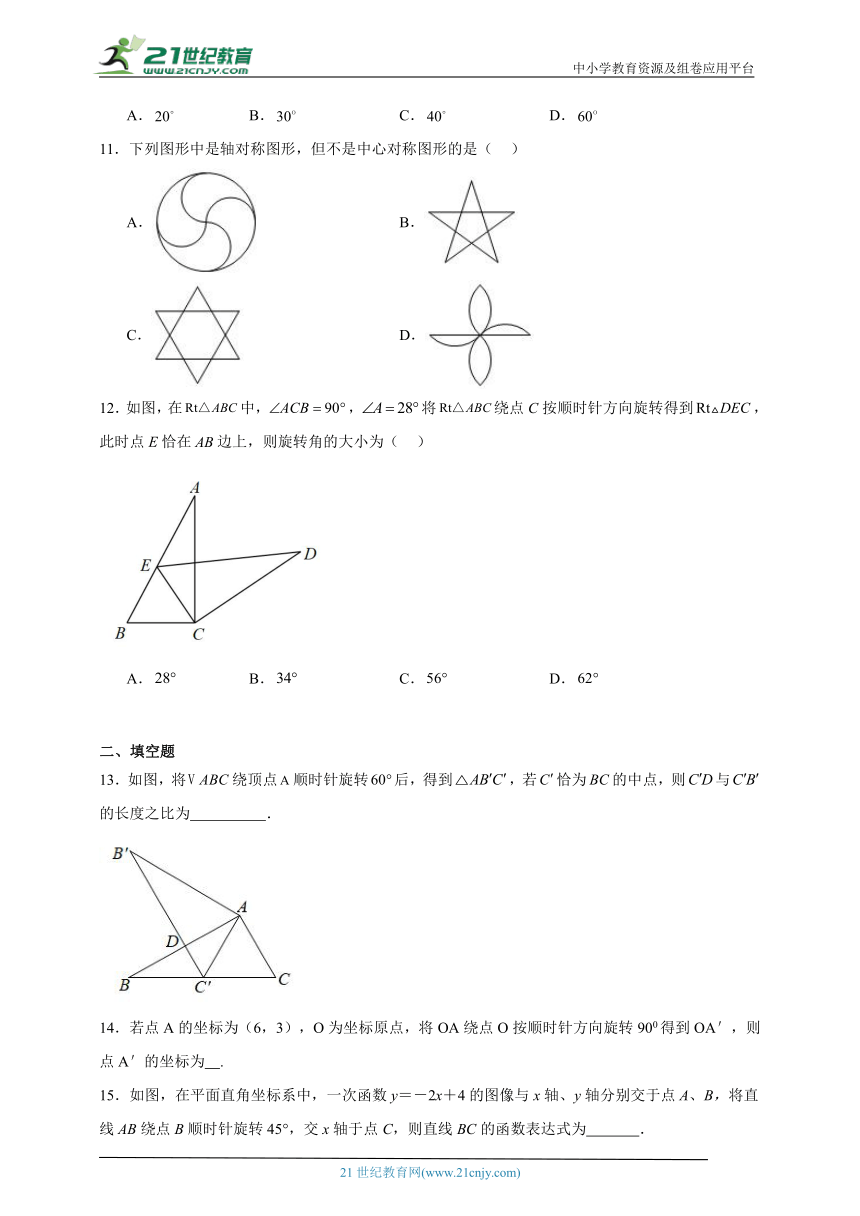
A.和 B.和 C.和 D.和
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.如图,将绕点逆时针旋转得到,延长交于点,若,则的度数是( )
A. B. C. D.
5.下列地铁标志中,既是轴对称图形又是中心对称图形的是( )
A.佛山地铁 B.广州地铁 C.南京地铁 D.深圳地铁
6.神木市的电话区号是0912,下列四个数字中,是中心对称图形的是( )
A. B. C. D.
7.下列图形中,不是中心对称图形的是( )
A. B. C. D.
8.如图,将△ABC绕点A逆时针旋转40°得到△ADE,其中点D恰好落在BC边上,则∠ADE等于( )
A. B. C. D.
9.剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术,民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.“对称美”是河南剪纸作品中重要的主题,下列剪纸作品中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
10.已知一个旋转对称图形是中心对称图形,那么下列度数不可能是这个图形最小旋转角的是( )
A. B. C. D.
11.下列图形中是轴对称图形,但不是中心对称图形的是( )
A. B.
C. D.
12.如图,在中,,将绕点C按顺时针方向旋转得到,此时点E恰在边上,则旋转角的大小为( )
A. B. C. D.
二、填空题
13.如图,将绕顶点顺时针旋转后,得到,若恰为的中点,则与的长度之比为 .
14.若点A的坐标为(6,3),O为坐标原点,将OA绕点O按顺时针方向旋转900得到OA',则点A'的坐标为 .
15.如图,在平面直角坐标系中,一次函数y=-2x+4的图像与x轴、y轴分别交于点A、B,将直线AB绕点B顺时针旋转45°,交x轴于点C,则直线BC的函数表达式为 .
16.如图,点E是边长为4的正方形内部一点,,将按逆时针方向旋转得到,连接,则的最小值为 .
17.若点与关于原点对称,则的值是 .
三、解答题
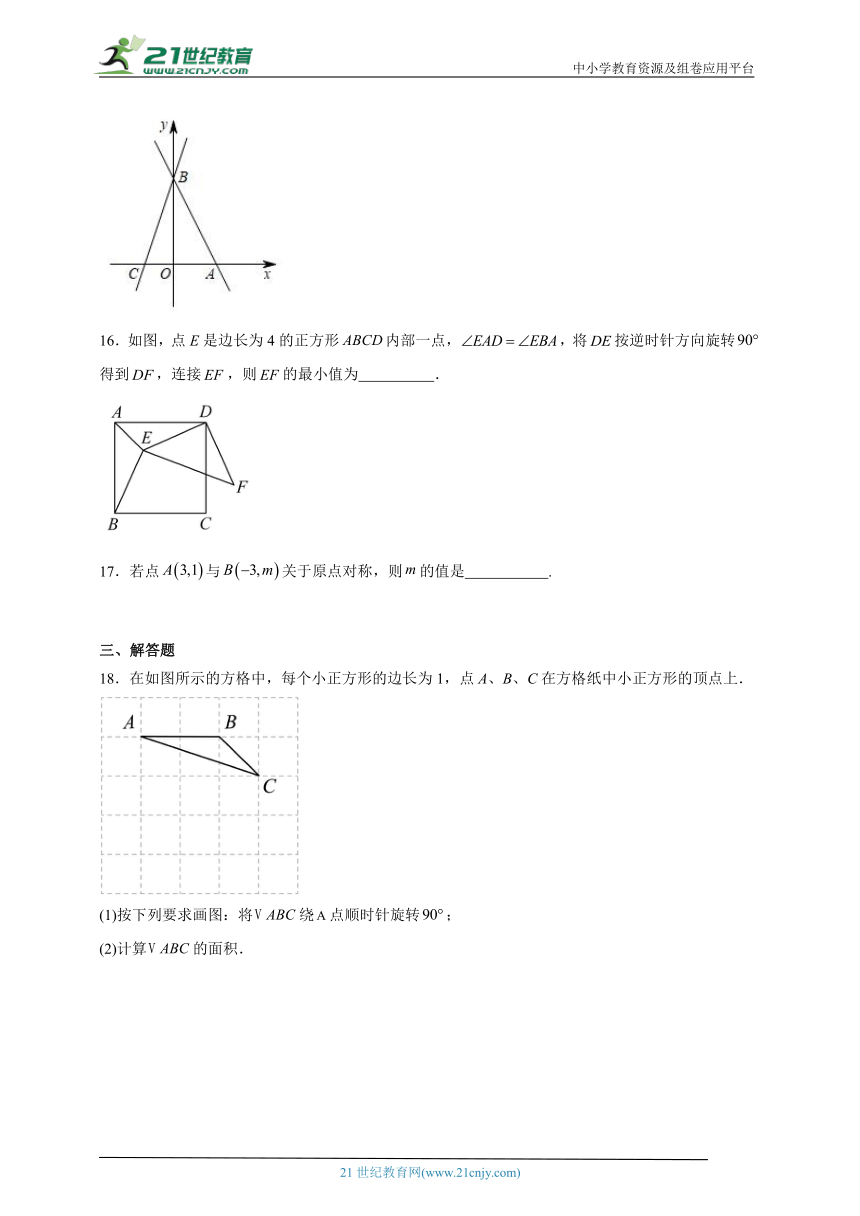
18.在如图所示的方格中,每个小正方形的边长为1,点A、B、C在方格纸中小正方形的顶点上.
(1)按下列要求画图:将绕点顺时针旋转;
(2)计算的面积.
19.如图,图中每个小方格都是边长为1个单位长度的正方形,在方格纸中的位置如图所示.
(1)请在图中建立平面直角坐标系,使得,两点的坐标分别为,,并写出点的坐标;
(2)在图中作出绕坐标原点旋转后的,并写出,,的坐标.
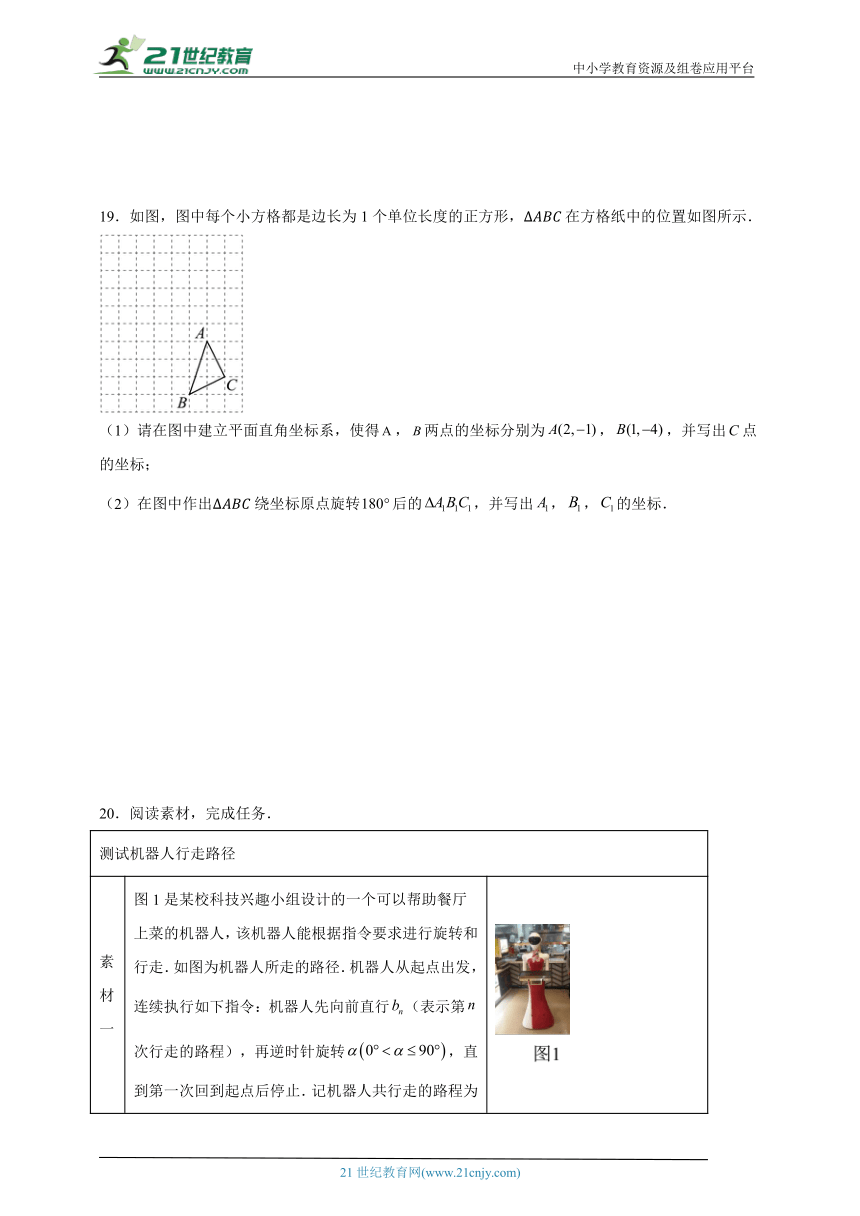
20.阅读素材,完成任务.
测试机器人行走路径
素材一 图1是某校科技兴趣小组设计的一个可以帮助餐厅上菜的机器人,该机器人能根据指令要求进行旋转和行走.如图为机器人所走的路径.机器人从起点出发,连续执行如下指令:机器人先向前直行(表示第次行走的路程),再逆时针旋转,直到第一次回到起点后停止.记机器人共行走的路程为,所走路径形成的封闭图形的面积为S.
素材二 如图2,当每次直行路程均为1(即),时,机器人的运动路径为,机器人共走的路程,由图2图3易得所走路径形成的封闭图形的面积为.
素材三 如图4,若,机器人执行六次指令后回到起点处停止.
解决问题
任务 固定变量 探索变量 探索内容
任务一 直行路程 旋转角度与路程
任务二 旋转角度 直行路程 若,求与的值.
任务三 旋转角度,路程 路径形成的封闭图形面积S. 若,请直接写出与之间的数量关系,并求出当S最大时的值.
21.已知,在四边形中,,连接.
(1)如图1,若,,,求的面积;
(2)如图2,若,平分,求证:;
(3)如图3,在(2)的条件下,若点P是射线上一动点,连接.将线段绕着点D顺时针旋转,点P的对应点为,若,请直接写出的最小值.
22.某研究性学习小组在学习第三章第4节《简单的图案设计》时,发现了一种特殊的四边形,如图1,在四边形中,,,我们把这种四边形称为“等补四边形”.如何求“等补四边形”的面积呢?
探究一:
(1)如图2,已知“等补四边形”,若,将“等补四边形”绕点顺时针旋转,可以形成一个直角梯形(如图3).若,,则“等补四边形”的面积为______
探究二:
(2)如图4,已知“等补四边形”,若,将“等补四边形”绕点顺时针旋转,再将得到的四边形按上述方式旋转,可以形成一个等边三角形(如图5).若,,求“等补四边形”的面积.
探究三:
(3)由以上探究可知,对一些特殊的“等补四边形”,只需要知道,的长度,就可以求它的面积.那么如图6,已知“等补四边形”,连接,若,,,试求出“等补四边形”的面积(用含,的代数式表示).
23.如图,四边形是正方形,是等边三角形,为对角线(不含点)上任意一点,将绕点逆时针旋转得到,连接、、.
(1)求证:;
(2)当的最小值为时,求正方形的边长.
24.如图,和中,,,,连接,点M,N,P分别是的中点.
(1)请你判断的形状,并证明你的结论.
(2)将绕点A旋转,若,请直接写出周长的最大值与最小值.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C B D A B D C C
题号 11 12
答案 B C
1.D
2.A
3.C
4.B
5.D
6.A
7.B
8.D
9.C
10.C
11.B
12.C
13.1:4
14.(3,-6)
15./y=4+3x
16.
17.
18.(1)略
(2)1
19.(1)点坐标;(2),,的坐标分别是
20.(1)12;8;5;(2),;(3);
21.(1)
(2)略
(3)的最小值是
22.(1);(2);(3)
23.(1)略
(2)正方形的边长为
24.(1)是等腰直角三角形
(2)周长最小值为。最大值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十三章旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2023年9月21日,“天宫课堂”第四课在中国空间站成功开讲,本次太空授课活动激发了广大青少年不断追寻“科学梦”,实现“航天梦”的热情.下列相关卡通图标分别是“星球”“宇航员”“星系”和“黑洞”,其中是中心对称图形的是( )
B.
C. D.
2.如图,在中,已知,,,若将绕点C时针方向旋转180 ,得到,则,的坐标依次是( )
A.和 B.和 C.和 D.和
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.如图,将绕点逆时针旋转得到,延长交于点,若,则的度数是( )
A. B. C. D.
5.下列地铁标志中,既是轴对称图形又是中心对称图形的是( )
A.佛山地铁 B.广州地铁 C.南京地铁 D.深圳地铁
6.神木市的电话区号是0912,下列四个数字中,是中心对称图形的是( )
A. B. C. D.
7.下列图形中,不是中心对称图形的是( )
A. B. C. D.
8.如图,将△ABC绕点A逆时针旋转40°得到△ADE,其中点D恰好落在BC边上,则∠ADE等于( )
A. B. C. D.
9.剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术,民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.“对称美”是河南剪纸作品中重要的主题,下列剪纸作品中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
10.已知一个旋转对称图形是中心对称图形,那么下列度数不可能是这个图形最小旋转角的是( )
A. B. C. D.
11.下列图形中是轴对称图形,但不是中心对称图形的是( )
A. B.
C. D.
12.如图,在中,,将绕点C按顺时针方向旋转得到,此时点E恰在边上,则旋转角的大小为( )
A. B. C. D.
二、填空题
13.如图,将绕顶点顺时针旋转后,得到,若恰为的中点,则与的长度之比为 .
14.若点A的坐标为(6,3),O为坐标原点,将OA绕点O按顺时针方向旋转900得到OA',则点A'的坐标为 .
15.如图,在平面直角坐标系中,一次函数y=-2x+4的图像与x轴、y轴分别交于点A、B,将直线AB绕点B顺时针旋转45°,交x轴于点C,则直线BC的函数表达式为 .
16.如图,点E是边长为4的正方形内部一点,,将按逆时针方向旋转得到,连接,则的最小值为 .
17.若点与关于原点对称,则的值是 .
三、解答题
18.在如图所示的方格中,每个小正方形的边长为1,点A、B、C在方格纸中小正方形的顶点上.
(1)按下列要求画图:将绕点顺时针旋转;
(2)计算的面积.
19.如图,图中每个小方格都是边长为1个单位长度的正方形,在方格纸中的位置如图所示.
(1)请在图中建立平面直角坐标系,使得,两点的坐标分别为,,并写出点的坐标;
(2)在图中作出绕坐标原点旋转后的,并写出,,的坐标.
20.阅读素材,完成任务.
测试机器人行走路径
素材一 图1是某校科技兴趣小组设计的一个可以帮助餐厅上菜的机器人,该机器人能根据指令要求进行旋转和行走.如图为机器人所走的路径.机器人从起点出发,连续执行如下指令:机器人先向前直行(表示第次行走的路程),再逆时针旋转,直到第一次回到起点后停止.记机器人共行走的路程为,所走路径形成的封闭图形的面积为S.
素材二 如图2,当每次直行路程均为1(即),时,机器人的运动路径为,机器人共走的路程,由图2图3易得所走路径形成的封闭图形的面积为.
素材三 如图4,若,机器人执行六次指令后回到起点处停止.
解决问题
任务 固定变量 探索变量 探索内容
任务一 直行路程 旋转角度与路程
任务二 旋转角度 直行路程 若,求与的值.
任务三 旋转角度,路程 路径形成的封闭图形面积S. 若,请直接写出与之间的数量关系,并求出当S最大时的值.
21.已知,在四边形中,,连接.
(1)如图1,若,,,求的面积;
(2)如图2,若,平分,求证:;
(3)如图3,在(2)的条件下,若点P是射线上一动点,连接.将线段绕着点D顺时针旋转,点P的对应点为,若,请直接写出的最小值.
22.某研究性学习小组在学习第三章第4节《简单的图案设计》时,发现了一种特殊的四边形,如图1,在四边形中,,,我们把这种四边形称为“等补四边形”.如何求“等补四边形”的面积呢?
探究一:
(1)如图2,已知“等补四边形”,若,将“等补四边形”绕点顺时针旋转,可以形成一个直角梯形(如图3).若,,则“等补四边形”的面积为______
探究二:
(2)如图4,已知“等补四边形”,若,将“等补四边形”绕点顺时针旋转,再将得到的四边形按上述方式旋转,可以形成一个等边三角形(如图5).若,,求“等补四边形”的面积.
探究三:
(3)由以上探究可知,对一些特殊的“等补四边形”,只需要知道,的长度,就可以求它的面积.那么如图6,已知“等补四边形”,连接,若,,,试求出“等补四边形”的面积(用含,的代数式表示).
23.如图,四边形是正方形,是等边三角形,为对角线(不含点)上任意一点,将绕点逆时针旋转得到,连接、、.
(1)求证:;
(2)当的最小值为时,求正方形的边长.
24.如图,和中,,,,连接,点M,N,P分别是的中点.
(1)请你判断的形状,并证明你的结论.
(2)将绕点A旋转,若,请直接写出周长的最大值与最小值.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C B D A B D C C
题号 11 12
答案 B C
1.D
2.A
3.C
4.B
5.D
6.A
7.B
8.D
9.C
10.C
11.B
12.C
13.1:4
14.(3,-6)
15./y=4+3x
16.
17.
18.(1)略
(2)1
19.(1)点坐标;(2),,的坐标分别是
20.(1)12;8;5;(2),;(3);
21.(1)
(2)略
(3)的最小值是
22.(1);(2);(3)
23.(1)略
(2)正方形的边长为
24.(1)是等腰直角三角形
(2)周长最小值为。最大值为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
