第十四章整式的乘法与因式分解单元测试(含答案)
文档属性
| 名称 | 第十四章整式的乘法与因式分解单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 460.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十四章整式的乘法与因式分解
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列等式中,不一定成立的是( )
A.3m2﹣2m2=m2 B.m2 m3=m5 C.(m+1)2=m2+1 D.(m2)3=m6
2.下列计算正确的是( )
A.3x2y+5yx2=8x2y B.2x 3x=6x
C.(3x3)3=9x9 D.(﹣x)3 (﹣3x)=﹣3x4
3.下列各式中,正确的是( )
A. B. C. D.
4.当时,代数式的值是( )
A.-4 B.-2 C.2 D.4
5.下列运算正确的是( )
A. B. C. D.
6.下列计算结果正确的是( )
A. B.
C. D.
7.下列运算正确的是( )
A. B. C. D.
8.下列运算正确的是( )
A. B. C. D.
9.若,则n等于( )
A.2 B.4 C.6 D.8
10.已知(x-1)2=2,则代数式2+5的值为 ( )
A.4 B.5 C.6 D.7
11.一个长方体的长、宽、高分别为3x-4,2x和x,则它的体积等于( )
A. B.
C. D.
12.下列各式是完全平方公式的是( )
A.16x -4xy+y B.m +mn+n C.9a -24ab+16b D.c +2cd+d
二、填空题
13.分解因式: .
14.计算 .
15.已知,那么 , .
16.计算:
(1) .
(2) .
(3) .
(4) .
17.因式分解: .
三、解答题
18.计算:
①把25.72°用度、分、秒表示;
先化简,再求值:
②[(xy+2)(xy-2)-2(x2y2-2)]÷(xy),其中x=10,y=.
③(x+y)2-(-xy3-3x2y2)÷(-xy),其中x=2,y=1.
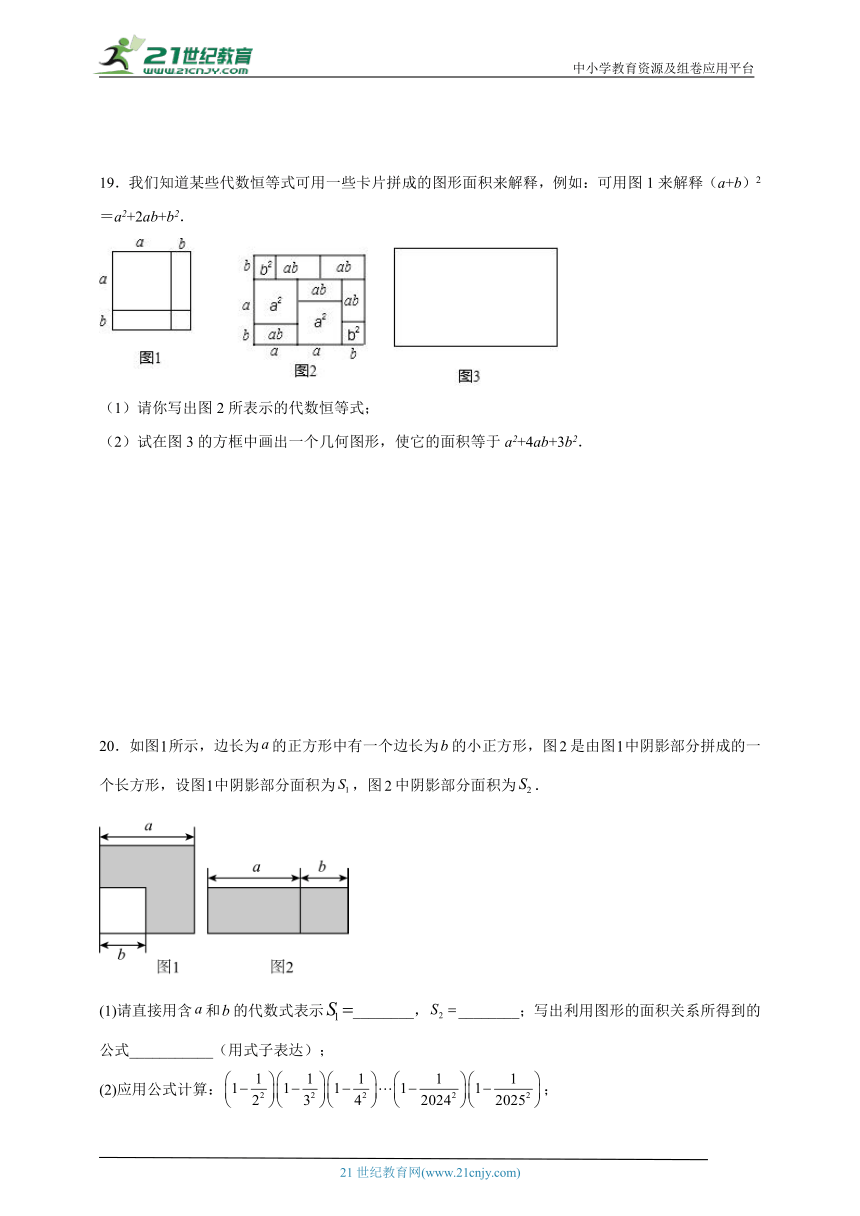
19.我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:可用图1来解释(a+b)2=a2+2ab+b2.
(1)请你写出图2所表示的代数恒等式;
(2)试在图3的方框中画出一个几何图形,使它的面积等于a2+4ab+3b2.
20.如图所示,边长为的正方形中有一个边长为的小正方形,图是由图中阴影部分拼成的一个长方形,设图中阴影部分面积为,图中阴影部分面积为.
(1)请直接用含和的代数式表示________,________;写出利用图形的面积关系所得到的公式___________(用式子表达);
(2)应用公式计算:;
(3)应用公式计算:.
21.如图,某新建高铁站广场前有一块长为米,宽为米的长方形空地,计划在中间留一个长方形喷泉(图中阴影部分),喷泉四周留有宽度均为米的人行通道.
(1)请用代数式表示喷泉的面积并化简;
(2)喷泉建成后,需给人行通道铺上地砖方便旅客通行,若每块地砖的面积是平方米,则刚好铺满不留缝隙,求需要这样的地砖多少块.
22.如图所示的是人民公园的一块长为米,宽为米的空地,预计在空地上建造一个网红打卡观景台(阴影部分).
(1)请用m,n表示观景台的面积;(结果化为最简)
(2)如果修建观景台的费用为200元/平方米.且已知米,米,那么修建观景台需要费用多少元?
23.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
…
按照以上规律,解决下列问题:
(1)写出第5个等式:______.
(2)写出你猜想的第个等式(用含的式子表示),并证明.
24.已知整数a,b,m,n满足.
(1)求证:为非负数;
(2)若n为偶数,判断是否可以为奇数,说明你理由.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B A B B B D B C
题号 11 12
答案 C C
1.C
2.A
3.B
4.A
5.B
6.B
7.B
8.D
9.B
10.C
11.C
12.C
13.
14./
15. 15
16. ; ; ; .
17.
18.①;②-xy,;③,2
19.(1)(a+2b)(2a+b)=2a2+5ab+2b2;(2)略
20.(1);;
(2)
(3)
21.(1),
(2)块
22.(1)观景台的面积为平方米
(2)修建观景台需要费用为19600元
23.(1)
(2)
24.(1)略
(2)不可以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十四章整式的乘法与因式分解
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列等式中,不一定成立的是( )
A.3m2﹣2m2=m2 B.m2 m3=m5 C.(m+1)2=m2+1 D.(m2)3=m6
2.下列计算正确的是( )
A.3x2y+5yx2=8x2y B.2x 3x=6x
C.(3x3)3=9x9 D.(﹣x)3 (﹣3x)=﹣3x4
3.下列各式中,正确的是( )
A. B. C. D.
4.当时,代数式的值是( )
A.-4 B.-2 C.2 D.4
5.下列运算正确的是( )
A. B. C. D.
6.下列计算结果正确的是( )
A. B.
C. D.
7.下列运算正确的是( )
A. B. C. D.
8.下列运算正确的是( )
A. B. C. D.
9.若,则n等于( )
A.2 B.4 C.6 D.8
10.已知(x-1)2=2,则代数式2+5的值为 ( )
A.4 B.5 C.6 D.7
11.一个长方体的长、宽、高分别为3x-4,2x和x,则它的体积等于( )
A. B.
C. D.
12.下列各式是完全平方公式的是( )
A.16x -4xy+y B.m +mn+n C.9a -24ab+16b D.c +2cd+d
二、填空题
13.分解因式: .
14.计算 .
15.已知,那么 , .
16.计算:
(1) .
(2) .
(3) .
(4) .
17.因式分解: .
三、解答题
18.计算:
①把25.72°用度、分、秒表示;
先化简,再求值:
②[(xy+2)(xy-2)-2(x2y2-2)]÷(xy),其中x=10,y=.
③(x+y)2-(-xy3-3x2y2)÷(-xy),其中x=2,y=1.
19.我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:可用图1来解释(a+b)2=a2+2ab+b2.
(1)请你写出图2所表示的代数恒等式;
(2)试在图3的方框中画出一个几何图形,使它的面积等于a2+4ab+3b2.
20.如图所示,边长为的正方形中有一个边长为的小正方形,图是由图中阴影部分拼成的一个长方形,设图中阴影部分面积为,图中阴影部分面积为.
(1)请直接用含和的代数式表示________,________;写出利用图形的面积关系所得到的公式___________(用式子表达);
(2)应用公式计算:;
(3)应用公式计算:.
21.如图,某新建高铁站广场前有一块长为米,宽为米的长方形空地,计划在中间留一个长方形喷泉(图中阴影部分),喷泉四周留有宽度均为米的人行通道.
(1)请用代数式表示喷泉的面积并化简;
(2)喷泉建成后,需给人行通道铺上地砖方便旅客通行,若每块地砖的面积是平方米,则刚好铺满不留缝隙,求需要这样的地砖多少块.
22.如图所示的是人民公园的一块长为米,宽为米的空地,预计在空地上建造一个网红打卡观景台(阴影部分).
(1)请用m,n表示观景台的面积;(结果化为最简)
(2)如果修建观景台的费用为200元/平方米.且已知米,米,那么修建观景台需要费用多少元?
23.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
…
按照以上规律,解决下列问题:
(1)写出第5个等式:______.
(2)写出你猜想的第个等式(用含的式子表示),并证明.
24.已知整数a,b,m,n满足.
(1)求证:为非负数;
(2)若n为偶数,判断是否可以为奇数,说明你理由.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B A B B B D B C
题号 11 12
答案 C C
1.C
2.A
3.B
4.A
5.B
6.B
7.B
8.D
9.B
10.C
11.C
12.C
13.
14./
15. 15
16. ; ; ; .
17.
18.①;②-xy,;③,2
19.(1)(a+2b)(2a+b)=2a2+5ab+2b2;(2)略
20.(1);;
(2)
(3)
21.(1),
(2)块
22.(1)观景台的面积为平方米
(2)修建观景台需要费用为19600元
23.(1)
(2)
24.(1)略
(2)不可以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
