第十二章全等三角形同步练习 人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形同步练习 人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 07:12:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十二章全等三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,△ABC≌△ADE,AB=AD,AC=AE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=15°,∠B=30°,则∠1的度数为( ).
A.50° B.60° C.40° D.20°
2.下列选项所给条件能画出唯一的是( )
A.,, B.,,
C., D.,,
3.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
①BC+AD=AB ; ②E为CD中点
③∠AEB=90°; ④S△ABE=S四边形ABCD
A.1 B.2 C.3 D.4
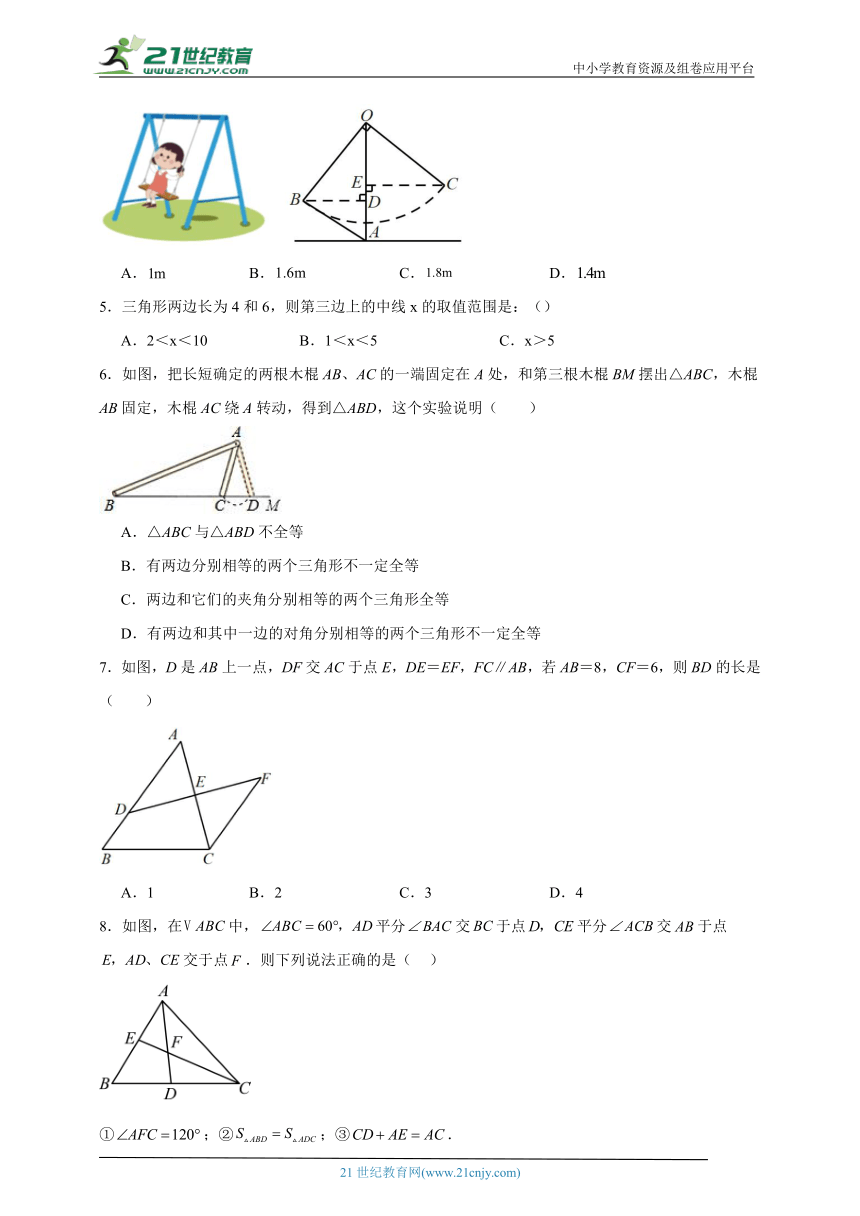
4.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到的水平距离、分别为和,.爸爸在C处接住小丽时,小丽距离地面的高度是( )
A. B. C. D.
5.三角形两边长为4和6,则第三边上的中线x的取值范围是:()
A.2<x<10 B.1<x<5 C.x>5
6.如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
7.如图,D是AB上一点,DF交AC于点E,DE=EF,FC∥AB,若AB=8,CF=6,则BD的长是( )
A.1 B.2 C.3 D.4
8.如图,在中,平分交于点平分交于点交于点.则下列说法正确的是( )
①;②;③.
A.①② B.①③ C.②③ D.①②③
9.在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0) B.(4,0) C.(4.﹣2) D.(4,﹣3)
10.如图所示,∠1=∠2,∠3=∠4,若证得BD=CD,则所用的判定两三角形全等的依据是( )
A.角角角 B.角边角 C.边角边 D.角角边
11.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC
C.∠B=∠E D.∠BAC=∠EAD
12.如图,正方形ABCD中,直线l经过点A,分别过点D、B作l的垂线,垂足分别是点E、F,连接DF,若AF=2,则△DAF的面积是( )
A.2 B. C.3 D.4
二、填空题
13.如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD= cm.
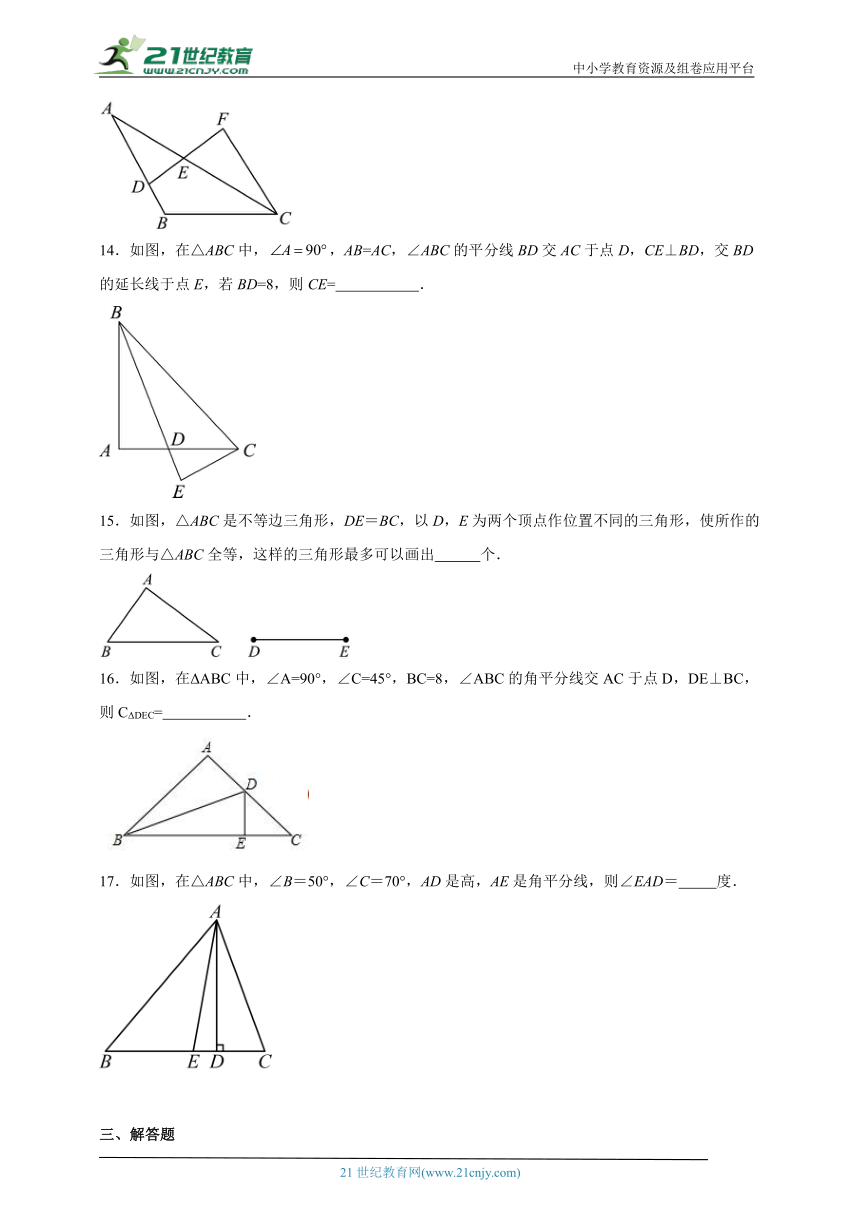
14.如图,在△ABC中,,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=8,则CE= .
15.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
16.如图,在ΔABC中,∠A=90°,∠C=45°,BC=8,∠ABC的角平分线交AC于点D,DE⊥BC,则CΔDEC= .
17.如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,则∠EAD= 度.
三、解答题
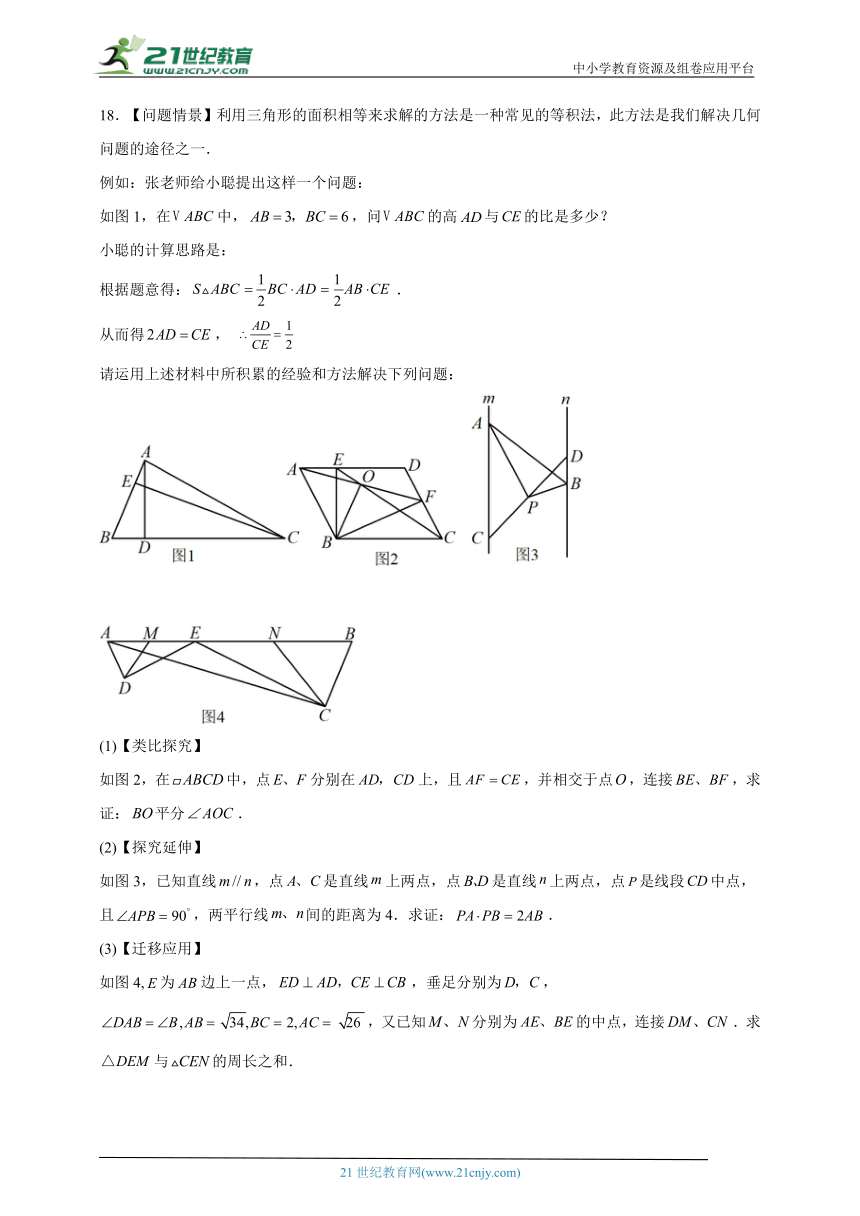
18.【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在中,,问的高与的比是多少?
小聪的计算思路是:
根据题意得:.
从而得,
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在中,点分别在上,且,并相交于点,连接,求证:平分.
(2)【探究延伸】
如图3,已知直线,点是直线上两点,点是直线上两点,点是线段中点,且,两平行线间的距离为4.求证:.
(3)【迁移应用】
如图4,为边上一点,,垂足分别为,,又已知分别为的中点,连接.求与的周长之和.
19.如图,在中,点D在边的延长线上,过点D作射线,点E是射线上一个定点.
(1)用尺规完成以下基本作图:在射线上方作,与的延长线交于点F.(保留作图痕迹)
(2)在(1)问条件下,若,求证:
请把以下的解题过程补充完整.
证明:(已知)
(① )
(已知)
② (等式的性质)
在和中
③ (全等三角形的对应角相等)
(④ )
20.公路上,两站相距千米,为两所学校,于点,于点,如图,已知千米,现在要在公路上建一报亭,使得两所学校到的距离相等,且,问:应建在距离站多远处?学校到公路的距离是多少千米?
21.风力发电因其既可再生又不破坏生态环境的特点,深受各国欢迎,并被大规模推广和实施.在一次旅途中,青青和依依想运用所学知识测量图1中某风力发电机组塔架的高度,如图2,青青站在地面上的点D处,眼睛位于点C处时,测得塔架顶端A的仰角的度数,依依从地面上的点G处竖直向上放飞一架无人机,当无人机位于点F处时,测得地面上点D的俯角的度数,恰好发现与互余,已知地面上三点在同一水平直线上,,,请你求出该风力发电机组塔架的高度.
22.如图,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,在观测点B的北偏西方向上,海岛D在观测点B的正北方,在观测点A的北偏东方向上,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
23.完成下面的证明过程.
已知:如图,,于点E,于点F,.
求证:.
证明:∵,(已知)
∴.( )
∵,,(已知)
∴______.( )
∵,(已知)
∴______,( )
即______.
在和中,
∵,
∴.( )
24.如图,点D在BC上,∠1=∠2,AE=AC,下面有三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并进行证明.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D B D B B D D
题号 11 12
答案 C A
1.B
2.A
3.D
4.D
5.B
6.D
7.B
8.B
9.D
10.D
11.C
12.A
13.4
14.4
15.4
16.8.
17.10°
18.(1)略
(2)略
(3)
19.(1)略
(2)①两直线平行,同位角相等;②;③;④同位角相等,两直线平行;
20.应建在距离站千米处,学校到公路的距离是千米
21.该风力发电机组塔架的高度为
22.相等
23.两直线平行,内错角相等;;垂直的定义;;线段的和与差;;;
24.略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十二章全等三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,△ABC≌△ADE,AB=AD,AC=AE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=15°,∠B=30°,则∠1的度数为( ).
A.50° B.60° C.40° D.20°
2.下列选项所给条件能画出唯一的是( )
A.,, B.,,
C., D.,,
3.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
①BC+AD=AB ; ②E为CD中点
③∠AEB=90°; ④S△ABE=S四边形ABCD
A.1 B.2 C.3 D.4
4.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到的水平距离、分别为和,.爸爸在C处接住小丽时,小丽距离地面的高度是( )
A. B. C. D.
5.三角形两边长为4和6,则第三边上的中线x的取值范围是:()
A.2<x<10 B.1<x<5 C.x>5
6.如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
7.如图,D是AB上一点,DF交AC于点E,DE=EF,FC∥AB,若AB=8,CF=6,则BD的长是( )
A.1 B.2 C.3 D.4
8.如图,在中,平分交于点平分交于点交于点.则下列说法正确的是( )
①;②;③.
A.①② B.①③ C.②③ D.①②③
9.在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0) B.(4,0) C.(4.﹣2) D.(4,﹣3)
10.如图所示,∠1=∠2,∠3=∠4,若证得BD=CD,则所用的判定两三角形全等的依据是( )
A.角角角 B.角边角 C.边角边 D.角角边
11.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
A.BC=ED B.∠BAD=∠EAC
C.∠B=∠E D.∠BAC=∠EAD
12.如图,正方形ABCD中,直线l经过点A,分别过点D、B作l的垂线,垂足分别是点E、F,连接DF,若AF=2,则△DAF的面积是( )
A.2 B. C.3 D.4
二、填空题
13.如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD= cm.
14.如图,在△ABC中,,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=8,则CE= .
15.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
16.如图,在ΔABC中,∠A=90°,∠C=45°,BC=8,∠ABC的角平分线交AC于点D,DE⊥BC,则CΔDEC= .
17.如图,在△ABC中,∠B=50°,∠C=70°,AD是高,AE是角平分线,则∠EAD= 度.
三、解答题
18.【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在中,,问的高与的比是多少?
小聪的计算思路是:
根据题意得:.
从而得,
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在中,点分别在上,且,并相交于点,连接,求证:平分.
(2)【探究延伸】
如图3,已知直线,点是直线上两点,点是直线上两点,点是线段中点,且,两平行线间的距离为4.求证:.
(3)【迁移应用】
如图4,为边上一点,,垂足分别为,,又已知分别为的中点,连接.求与的周长之和.
19.如图,在中,点D在边的延长线上,过点D作射线,点E是射线上一个定点.
(1)用尺规完成以下基本作图:在射线上方作,与的延长线交于点F.(保留作图痕迹)
(2)在(1)问条件下,若,求证:
请把以下的解题过程补充完整.
证明:(已知)
(① )
(已知)
② (等式的性质)
在和中
③ (全等三角形的对应角相等)
(④ )
20.公路上,两站相距千米,为两所学校,于点,于点,如图,已知千米,现在要在公路上建一报亭,使得两所学校到的距离相等,且,问:应建在距离站多远处?学校到公路的距离是多少千米?
21.风力发电因其既可再生又不破坏生态环境的特点,深受各国欢迎,并被大规模推广和实施.在一次旅途中,青青和依依想运用所学知识测量图1中某风力发电机组塔架的高度,如图2,青青站在地面上的点D处,眼睛位于点C处时,测得塔架顶端A的仰角的度数,依依从地面上的点G处竖直向上放飞一架无人机,当无人机位于点F处时,测得地面上点D的俯角的度数,恰好发现与互余,已知地面上三点在同一水平直线上,,,请你求出该风力发电机组塔架的高度.
22.如图,海岛上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,在观测点B的北偏西方向上,海岛D在观测点B的正北方,在观测点A的北偏东方向上,那么海岛C、D到观测点A、B所在海岸的距离相等吗?为什么?
23.完成下面的证明过程.
已知:如图,,于点E,于点F,.
求证:.
证明:∵,(已知)
∴.( )
∵,,(已知)
∴______.( )
∵,(已知)
∴______,( )
即______.
在和中,
∵,
∴.( )
24.如图,点D在BC上,∠1=∠2,AE=AC,下面有三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并进行证明.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D B D B B D D
题号 11 12
答案 C A
1.B
2.A
3.D
4.D
5.B
6.D
7.B
8.B
9.D
10.D
11.C
12.A
13.4
14.4
15.4
16.8.
17.10°
18.(1)略
(2)略
(3)
19.(1)略
(2)①两直线平行,同位角相等;②;③;④同位角相等,两直线平行;
20.应建在距离站千米处,学校到公路的距离是千米
21.该风力发电机组塔架的高度为
22.相等
23.两直线平行,内错角相等;;垂直的定义;;线段的和与差;;;
24.略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
