22.3实际问题与二次函数同步练习(含答案)2024-2025学年人教版九年级数学上册
文档属性
| 名称 | 22.3实际问题与二次函数同步练习(含答案)2024-2025学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 398.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 14:30:11 | ||
图片预览




文档简介
22.3实际问题与二次函数同步练习2024-2025学年人教版九年级数学上册
一、单选题
1.已知一个直角三角形两直角边长的和为10,设其中一条直角边长为x,则直角三角形的面积y与x之间的函数关系式是( )
A.y=-x2+5x B.y=-x2+10x C.y=x2+5x D.y=x2+10x
2.某商品的进价为每件元,现在的售价为每件元,每星期可卖出件,市场调查反映:如调整价格,每降价元,每星期要多卖出件,则每星期售出商品的利润单位:元与每件降价单位:元之间的函数关系式是( )
A. B.
C. D.
3.从地面竖直向上抛出一小球,小球的高度与运动时间之间的函数关系如图所示,下列结论正确的是( )
A.小球在空中经过的路程是45m B.小球抛出3秒时,达到最大高度
C.小球抛出3秒时速度最快 D.小球的高度时,
4.在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为,当炮弹落到地面时,经过的时间为( )
A.40秒 B.45秒 C.50秒 D.55秒
5.如图,利用一个直角墙角修建一个的四边形储料场,其中.若新建墙与总长为,则该储料场的最大面积是( )
A. B. C. D.
6.小明在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 ,则小明此次成绩为( )
A.8米 B.10米 C.12米 D.14米
7.商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )
A.y=10(200﹣10x) B.y=200(10+x)
C.y=10(200﹣10x)2 D.y=(10+x)(200﹣10x)
8.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. B.
C. D.
9.如图1所示的矩形窗框ABCD的周长及其两条隔断EF、GH的总长为a米,且隔断EF、GH分别与矩形的两条邻边平行,设BC的长为x米,矩形ABCD的面积为y平方米,y关于x的函数图象如图2,则下列说法正确的是( )
A.矩形ABCD的最大面积为8平方米
B.y与x之间的函数关系式为y=-x2+2x
C.当x=4时,矩形ABCD的面积最大
D.a的值为12
10.如图,铅球的出手点C距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度3米,则铅球运行路线的解析式为( )
A.h=﹣t2 B.y=﹣t2+t
C.h=﹣t2+t+1 D.h=-t2+2t+1
二、填空题
11.超市销售的某商品进价10元/件.在销售过程中发现,该商品每天的销售量y(件)与售价x(元/件)之间满足函数关系式y=-5x+150,该商品售价定为 元/件时,每天销售该商品获利最大.
12.某学校准备修建一个面积为y平方米的矩形花圃,它的长比宽多10米,设花圃的宽为x米,则可列函数为 ,化为一般形式为 .
13.某服装店购进一批单价为50元的衬衫,如果按90元销售,那么每天可销售20件.经调查发现,这种衬衫的销售价每降低1元,其销售量相应增加2件.当降价 元时,该服装店的销售利润最大.
14.如图,在正方形ABCD中,AB=6,P,Q分别为BC,CD上一点,且BP=CQ,连接PQ,则PQ的最小值是 .
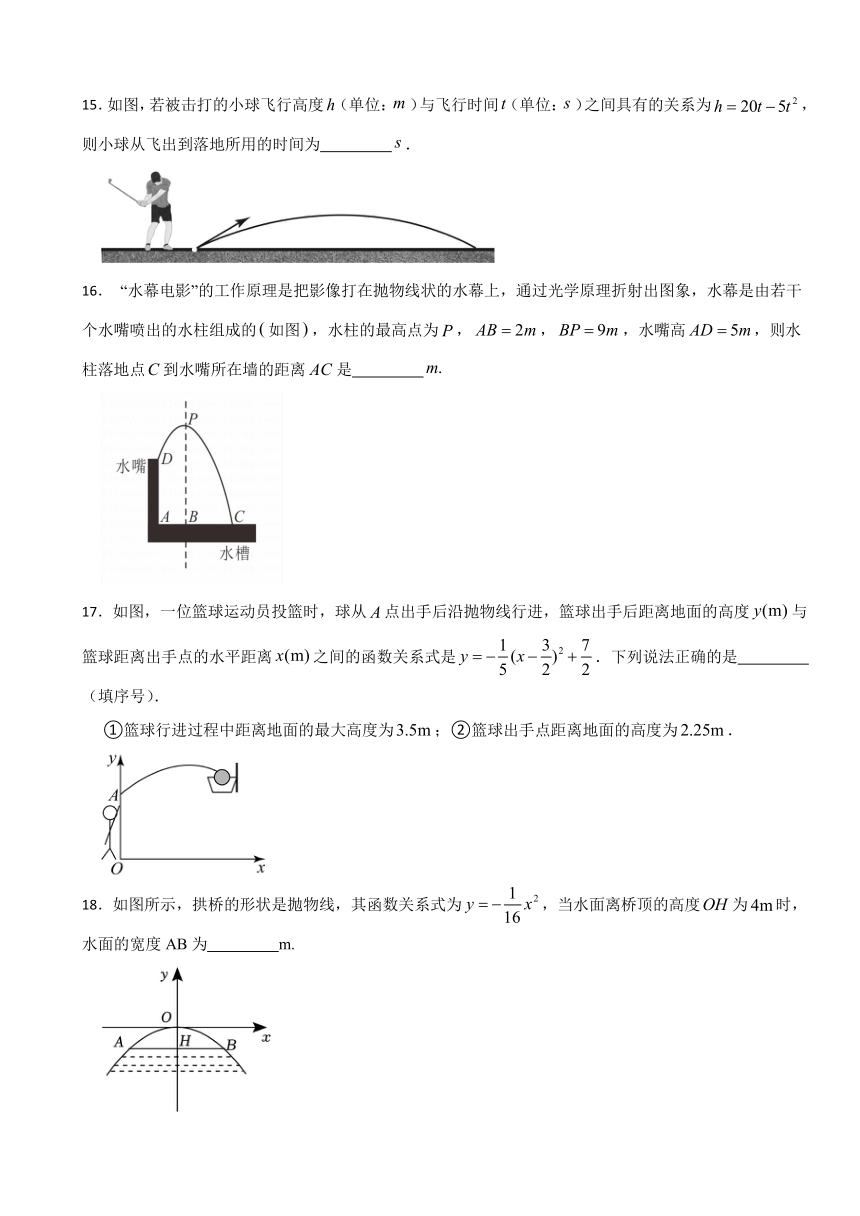
15.如图,若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系为,则小球从飞出到落地所用的时间为 .
16. “水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的如图,水柱的最高点为,,,水嘴高,则水柱落地点到水嘴所在墙的距离是
17.如图,一位篮球运动员投篮时,球从点出手后沿抛物线行进,篮球出手后距离地面的高度与篮球距离出手点的水平距离之间的函数关系式是.下列说法正确的是 (填序号).
①篮球行进过程中距离地面的最大高度为;②篮球出手点距离地面的高度为.
18.如图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为时,水面的宽度AB为 m.
三、解答题
19.如图,中,,动点P,Q分别从A,C两点同时出发,P点沿边向C以每秒3个单位长度的速度运动,Q点沿边向B以每秒4个单位长度的速度运动,当P,Q到达终点C,B时,运动停止,设运动时间为t(s).
(1)当运动停止时,的值为 ;
(2)设的面积为S.
①求S的表达式(用含t的式子表示,并注明t的取值范围);
②求当t为何值时,S取得最大值,这个最大值是多少?
20.某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米.不考虑墙体长度,问长方形的各边的长为多少时,长方形的面积最大,最大值是多少?
21.如图,四边形是一块边长为6米的正方形花圃,现将它改造为矩形的形状,其中点E在边上(不与点B重合),点G在的延长线上,,设的长为x米,改造后花圃的面积为y平方米.
(1)当改造后花圃的面积与原正方形花圃的面积相等时,求的长;
(2)当x为何值时,改造后的花圃的面积最大 并求出最大面积.
22. 学校准备将一块长,宽的矩形绿地扩建,如果长和宽都增加,设增加的面积是.
(1)求y与x之间的函数表达式;
(2)若要使绿地面积增加,则长与宽都要增加多少米?
23.如图,在斜坡底部点O处安装一个自动喷水装置,喷水头(视为点A)的高度(喷水头距喷水装置底部的距离)是米,自动喷水装置喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为米时,达到最大高度米.以点O为原点,自动喷水装置所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的函数关系式;
(2)斜坡上距离O水平距离为米处有一棵高度为米的小树,垂直水平地面,且M点到水平地面的距离为2米,绿化工人向左水平移动喷水装置后,水流恰好喷射到小树顶端的点N,求自动喷水装置向左水平平移(即抛物线向左)了多少米?
24.在“乡村振兴”行动中,某村办企业以A,B两种农作物为原料开发了一种有机产品,A原料的单价是B原料单价的1.5倍,若用900元收购A原料会比用900元收购B原料少100kg.生产该产品每盒需要A原料2kg和B原料4kg,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每盒每涨价1元,每天少销售10盒.
(1)求每盒产品的成本.(成本=原料费+其他成本)
(2)设每盒产品的售价是x元(x是整数),每天的利润是w元,求w关于x的函数表达式.(不需要写出自变量的取值范围)
(3)若每盒产品的售价不超过a元(a是大于60的常数,且是整数),直接写出每天的最大利润.
25. 如图,一位足球运动员在一次训练中,从球门正前方8m的A处射门,已知球门高OB为2.44m,球射向球门的路线可以看作是抛物线的一部分.当球飞行的水平距离为6m时,球达到最高点,此时球的竖直高度为3m.
现以O为原点,如图建立平面直角坐标系.
(1)求抛物线表示的二次函数解析式;
(2)通过计算判断球能否射进球门(忽略其他因素);
(3)若运动员射门路线的形状、最大高度均保持不变,则他应该带球向正后方移动 米射门,才能让足球经过点O正上方2.25m处.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】20
12.【答案】;
13.【答案】15
14.【答案】3
15.【答案】4.
16.【答案】5
17.【答案】①
18.【答案】16
19.【答案】(1)2
(2)①;②当时,取得最大值为
20.【答案】长方形的长为米,宽为米时,长方形的面积最大,最大是平方米
21.【答案】(1)BE=4米;(2)当x=2时,y的值最大为48平方米.
22.【答案】(1)解:y与x之间的函数表达式为:
(2)解:绿地面积增加时,矩形的长与宽都要增加2米
23.【答案】(1)
(2)3米
24.【答案】(1)解:设B原料单价为m元,则A原料单价为1.5m元,
根据题意,得,
解得m = 3,
∴1.5m = 4.5,
∴每盒产品的成本是:4.5×2+4×3+9=30(元),
答:每盒产品的成本为30元;
(2)解:根据题意,得
,
w关于x的函数解析式为:;
(3)解:由(2) 知,
w = -10x2+1400x-33000 =-10(x-70)2 +16000,
∴当a≥70时,每天最大利润为16000元,
当60 < a < 70时, 每天的最大利润为(- 10a2+1400a-33000)元.
25.【答案】(1)解:∵8-6=2,
∴抛物线的顶点坐标为(2,3),
设抛物线为 y=a(x-2)2+3,
把点A(8,0)代入得:36a+3=0,
解得a=-,
∴抛物线的函数解析式为:y=-(x-2)2+3;
(2)解:当x=0时,y=-×4+3=>2.44,
∴球不能射进球门.
(3)解:设小明带球向正后方移动m米,则移动后的抛物线为:y=-(x-2-m)2+3,
把点(0,2.25)代入得:2.25=-(0-2-m)2+3,
解得 m=-5(舍去)或m=1,
∴当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方2.25m处.
故答案为:1.
一、单选题
1.已知一个直角三角形两直角边长的和为10,设其中一条直角边长为x,则直角三角形的面积y与x之间的函数关系式是( )
A.y=-x2+5x B.y=-x2+10x C.y=x2+5x D.y=x2+10x
2.某商品的进价为每件元,现在的售价为每件元,每星期可卖出件,市场调查反映:如调整价格,每降价元,每星期要多卖出件,则每星期售出商品的利润单位:元与每件降价单位:元之间的函数关系式是( )
A. B.
C. D.
3.从地面竖直向上抛出一小球,小球的高度与运动时间之间的函数关系如图所示,下列结论正确的是( )
A.小球在空中经过的路程是45m B.小球抛出3秒时,达到最大高度
C.小球抛出3秒时速度最快 D.小球的高度时,
4.在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为,当炮弹落到地面时,经过的时间为( )
A.40秒 B.45秒 C.50秒 D.55秒
5.如图,利用一个直角墙角修建一个的四边形储料场,其中.若新建墙与总长为,则该储料场的最大面积是( )
A. B. C. D.
6.小明在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 ,则小明此次成绩为( )
A.8米 B.10米 C.12米 D.14米
7.商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )
A.y=10(200﹣10x) B.y=200(10+x)
C.y=10(200﹣10x)2 D.y=(10+x)(200﹣10x)
8.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. B.
C. D.
9.如图1所示的矩形窗框ABCD的周长及其两条隔断EF、GH的总长为a米,且隔断EF、GH分别与矩形的两条邻边平行,设BC的长为x米,矩形ABCD的面积为y平方米,y关于x的函数图象如图2,则下列说法正确的是( )
A.矩形ABCD的最大面积为8平方米
B.y与x之间的函数关系式为y=-x2+2x
C.当x=4时,矩形ABCD的面积最大
D.a的值为12
10.如图,铅球的出手点C距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度3米,则铅球运行路线的解析式为( )
A.h=﹣t2 B.y=﹣t2+t
C.h=﹣t2+t+1 D.h=-t2+2t+1
二、填空题
11.超市销售的某商品进价10元/件.在销售过程中发现,该商品每天的销售量y(件)与售价x(元/件)之间满足函数关系式y=-5x+150,该商品售价定为 元/件时,每天销售该商品获利最大.
12.某学校准备修建一个面积为y平方米的矩形花圃,它的长比宽多10米,设花圃的宽为x米,则可列函数为 ,化为一般形式为 .
13.某服装店购进一批单价为50元的衬衫,如果按90元销售,那么每天可销售20件.经调查发现,这种衬衫的销售价每降低1元,其销售量相应增加2件.当降价 元时,该服装店的销售利润最大.
14.如图,在正方形ABCD中,AB=6,P,Q分别为BC,CD上一点,且BP=CQ,连接PQ,则PQ的最小值是 .
15.如图,若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系为,则小球从飞出到落地所用的时间为 .
16. “水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的如图,水柱的最高点为,,,水嘴高,则水柱落地点到水嘴所在墙的距离是
17.如图,一位篮球运动员投篮时,球从点出手后沿抛物线行进,篮球出手后距离地面的高度与篮球距离出手点的水平距离之间的函数关系式是.下列说法正确的是 (填序号).
①篮球行进过程中距离地面的最大高度为;②篮球出手点距离地面的高度为.
18.如图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为时,水面的宽度AB为 m.
三、解答题
19.如图,中,,动点P,Q分别从A,C两点同时出发,P点沿边向C以每秒3个单位长度的速度运动,Q点沿边向B以每秒4个单位长度的速度运动,当P,Q到达终点C,B时,运动停止,设运动时间为t(s).
(1)当运动停止时,的值为 ;
(2)设的面积为S.
①求S的表达式(用含t的式子表示,并注明t的取值范围);
②求当t为何值时,S取得最大值,这个最大值是多少?
20.某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米.不考虑墙体长度,问长方形的各边的长为多少时,长方形的面积最大,最大值是多少?
21.如图,四边形是一块边长为6米的正方形花圃,现将它改造为矩形的形状,其中点E在边上(不与点B重合),点G在的延长线上,,设的长为x米,改造后花圃的面积为y平方米.
(1)当改造后花圃的面积与原正方形花圃的面积相等时,求的长;
(2)当x为何值时,改造后的花圃的面积最大 并求出最大面积.
22. 学校准备将一块长,宽的矩形绿地扩建,如果长和宽都增加,设增加的面积是.
(1)求y与x之间的函数表达式;
(2)若要使绿地面积增加,则长与宽都要增加多少米?
23.如图,在斜坡底部点O处安装一个自动喷水装置,喷水头(视为点A)的高度(喷水头距喷水装置底部的距离)是米,自动喷水装置喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为米时,达到最大高度米.以点O为原点,自动喷水装置所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的函数关系式;
(2)斜坡上距离O水平距离为米处有一棵高度为米的小树,垂直水平地面,且M点到水平地面的距离为2米,绿化工人向左水平移动喷水装置后,水流恰好喷射到小树顶端的点N,求自动喷水装置向左水平平移(即抛物线向左)了多少米?
24.在“乡村振兴”行动中,某村办企业以A,B两种农作物为原料开发了一种有机产品,A原料的单价是B原料单价的1.5倍,若用900元收购A原料会比用900元收购B原料少100kg.生产该产品每盒需要A原料2kg和B原料4kg,每盒还需其他成本9元.市场调查发现:该产品每盒的售价是60元时,每天可以销售500盒;每盒每涨价1元,每天少销售10盒.
(1)求每盒产品的成本.(成本=原料费+其他成本)
(2)设每盒产品的售价是x元(x是整数),每天的利润是w元,求w关于x的函数表达式.(不需要写出自变量的取值范围)
(3)若每盒产品的售价不超过a元(a是大于60的常数,且是整数),直接写出每天的最大利润.
25. 如图,一位足球运动员在一次训练中,从球门正前方8m的A处射门,已知球门高OB为2.44m,球射向球门的路线可以看作是抛物线的一部分.当球飞行的水平距离为6m时,球达到最高点,此时球的竖直高度为3m.
现以O为原点,如图建立平面直角坐标系.
(1)求抛物线表示的二次函数解析式;
(2)通过计算判断球能否射进球门(忽略其他因素);
(3)若运动员射门路线的形状、最大高度均保持不变,则他应该带球向正后方移动 米射门,才能让足球经过点O正上方2.25m处.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】C
11.【答案】20
12.【答案】;
13.【答案】15
14.【答案】3
15.【答案】4.
16.【答案】5
17.【答案】①
18.【答案】16
19.【答案】(1)2
(2)①;②当时,取得最大值为
20.【答案】长方形的长为米,宽为米时,长方形的面积最大,最大是平方米
21.【答案】(1)BE=4米;(2)当x=2时,y的值最大为48平方米.
22.【答案】(1)解:y与x之间的函数表达式为:
(2)解:绿地面积增加时,矩形的长与宽都要增加2米
23.【答案】(1)
(2)3米
24.【答案】(1)解:设B原料单价为m元,则A原料单价为1.5m元,
根据题意,得,
解得m = 3,
∴1.5m = 4.5,
∴每盒产品的成本是:4.5×2+4×3+9=30(元),
答:每盒产品的成本为30元;
(2)解:根据题意,得
,
w关于x的函数解析式为:;
(3)解:由(2) 知,
w = -10x2+1400x-33000 =-10(x-70)2 +16000,
∴当a≥70时,每天最大利润为16000元,
当60 < a < 70时, 每天的最大利润为(- 10a2+1400a-33000)元.
25.【答案】(1)解:∵8-6=2,
∴抛物线的顶点坐标为(2,3),
设抛物线为 y=a(x-2)2+3,
把点A(8,0)代入得:36a+3=0,
解得a=-,
∴抛物线的函数解析式为:y=-(x-2)2+3;
(2)解:当x=0时,y=-×4+3=>2.44,
∴球不能射进球门.
(3)解:设小明带球向正后方移动m米,则移动后的抛物线为:y=-(x-2-m)2+3,
把点(0,2.25)代入得:2.25=-(0-2-m)2+3,
解得 m=-5(舍去)或m=1,
∴当时他应该带球向正后方移动1米射门,才能让足球经过点O正上方2.25m处.
故答案为:1.
同课章节目录
