浙江省2024年九年级上册精选期中考试模拟卷B (含解析)
文档属性
| 名称 | 浙江省2024年九年级上册精选期中考试模拟卷B (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 12:05:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙江省2024年九年级上册精选期中考试模拟卷B
满分:120分 范围:第1-4章
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数一定是二次函数的是( )
A. B.y=3(x﹣1)2
C.y=ax2+bx+c D.y=2x+1
2.下列事件是必然事件的是( )
A.在足球赛中,弱队战胜强队 B.校园排球比赛,九年级一班获得冠军
C.从煮熟的鸡蛋里孵出小鸡 D.6月1日是儿童节
3.已知⊙O的半径为4,点P到圆心O的距离为4.8,则点P与⊙O的位置关系是( )
A.P在圆内 B.P在圆外 C.P在圆上 D.无法确定
4.a、b、c、d是成比例线段,其中a=6cm,b=3cm,c=4cm,则线段d的长可能为( )
A.2cm B.3cm C.4cm D.5cm
5.某射击运动员在同一条件下的射击成绩记录如表:
射击次数 100 200 400 800 1000
“射中九环以上”的次数 87 172 336 679 850
“射中九环以上”的频率 0.87 0.86 0.84 0.85 0.85
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.84 B.0.85 C.0.86 D.0.87
6.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么BF的长为( )
A. B. C. D.7
7.把抛物线y=﹣2x2先向左平移3个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=﹣2(x+3)2+2 B.y=﹣2(x﹣3)2+2
C.y=﹣2(x+3)2﹣2 D.y=﹣2(x﹣3)2﹣2
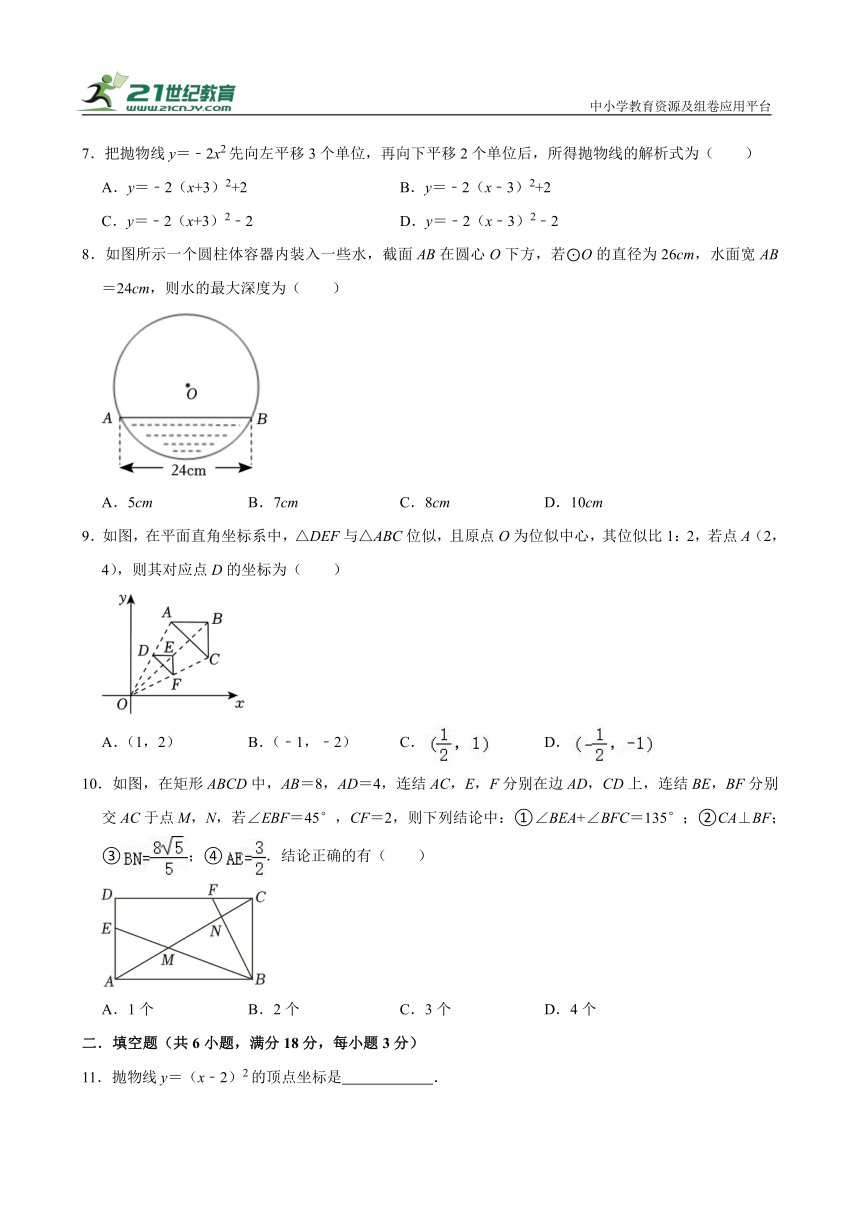
8.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为26cm,水面宽AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
9.如图,在平面直角坐标系中,△DEF与△ABC位似,且原点O为位似中心,其位似比1:2,若点A(2,4),则其对应点D的坐标为( )
A.(1,2) B.(﹣1,﹣2) C. D.
10.如图,在矩形ABCD中,AB=8,AD=4,连结AC,E,F分别在边AD,CD上,连结BE,BF分别交AC于点M,N,若∠EBF=45°,CF=2,则下列结论中:①∠BEA+∠BFC=135°;②CA⊥BF;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.抛物线y=(x﹣2)2的顶点坐标是 .
12.若,则= .
13.从1﹣9的数字卡片中,任意抽一张,抽到奇数的可能性是 .
14.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为 .
15.如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为 .
16.二次函数y=ax2+bx+c的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,﹣2<x1<﹣1,0<x2<1.下列结论中:①4a﹣2b+c<0;②2a﹣b<0;③b<﹣1;④;⑤(a+c)2<b2.
正确的有 (写出所有正确结论的序号).
三.解答题(共8小题,满分72分)
17.(6分)某数学兴趣小组测量校园内一棵树的高度.采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A.再用皮尺分别测量BF,DF,EF,观测者目高(CD)的长.利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D,EF⊥BD于点F.AB⊥BD于点B,BF=6米,DF=2米.EF=0.55米,CD=1.65米,求这棵树的高度(AB的长).
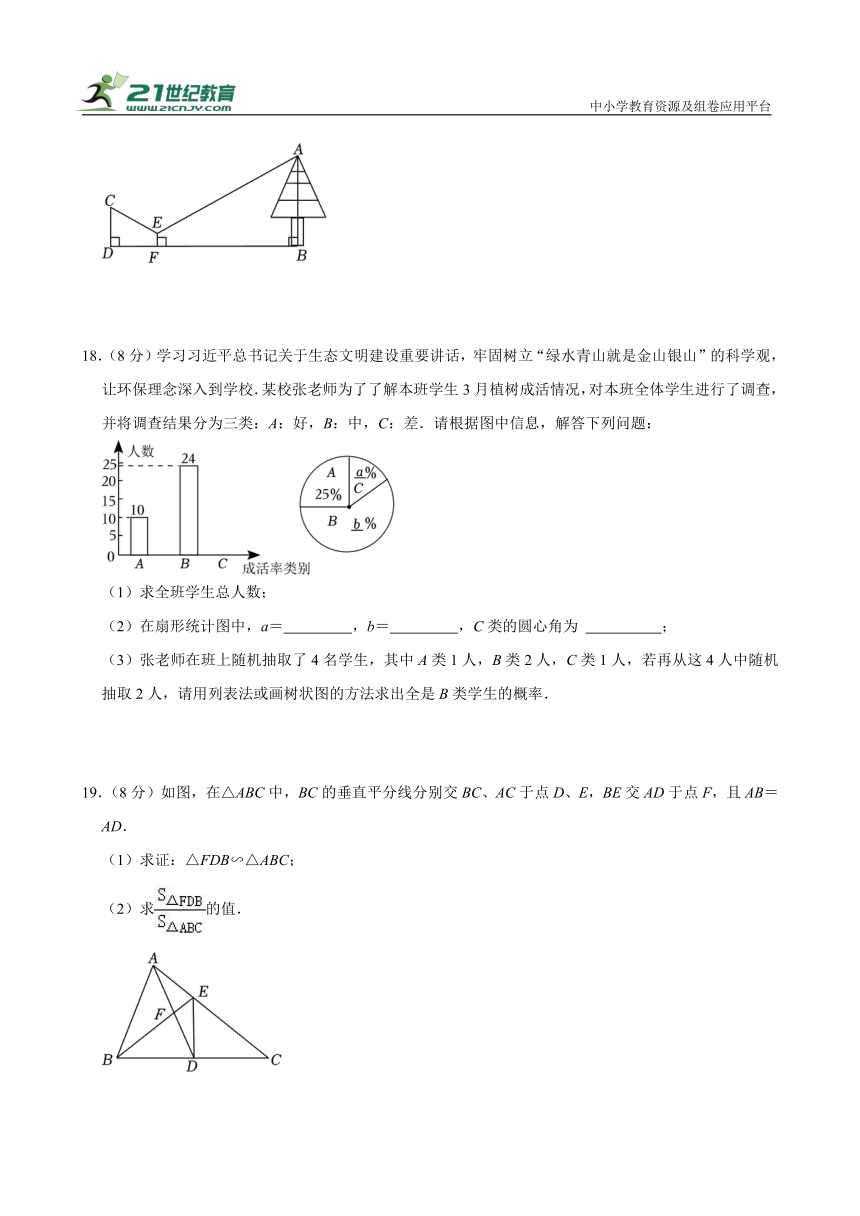
18.(8分)学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)在扇形统计图中,a= ,b= ,C类的圆心角为 ;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用列表法或画树状图的方法求出全是B类学生的概率.
19.(8分)如图,在△ABC中,BC的垂直平分线分别交BC、AC于点D、E,BE交AD于点F,且AB=AD.
(1)求证:△FDB∽△ABC;
(2)求的值.
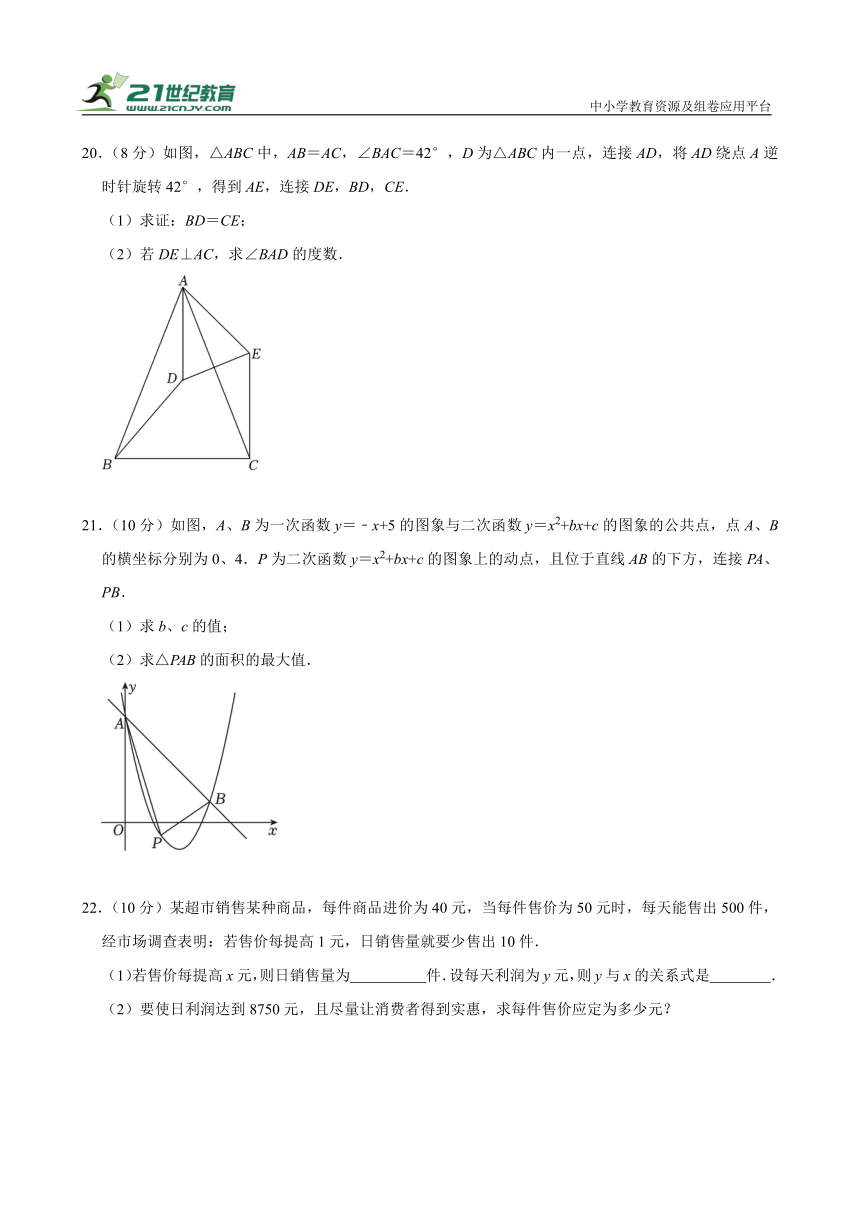
20.(8分)如图,△ABC中,AB=AC,∠BAC=42°,D为△ABC内一点,连接AD,将AD绕点A逆时针旋转42°,得到AE,连接DE,BD,CE.
(1)求证:BD=CE;
(2)若DE⊥AC,求∠BAD的度数.
21.(10分)如图,A、B为一次函数y=﹣x+5的图象与二次函数y=x2+bx+c的图象的公共点,点A、B的横坐标分别为0、4.P为二次函数y=x2+bx+c的图象上的动点,且位于直线AB的下方,连接PA、PB.
(1)求b、c的值;
(2)求△PAB的面积的最大值.
22.(10分)某超市销售某种商品,每件商品进价为40元,当每件售价为50元时,每天能售出500件,经市场调查表明:若售价每提高1元,日销售量就要少售出10件.
(1)若售价每提高x元,则日销售量为 件.设每天利润为y元,则y与x的关系式是 .
(2)要使日利润达到8750元,且尽量让消费者得到实惠,求每件售价应定为多少元?
23.(10分)如图,AB是⊙O的直径,D为AB上一点,C为⊙O上一点,且AD=AC,延长CD交⊙O于E,连CB.
(1)求证:∠CAB=2∠BCD;
(2)若∠BCE=15°,AB=6,求CE的长.
24.(12分)如图1,抛物线y=ax2+2x+c交x轴于A,B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上是否存在一点M,使得MO+MA的值最小,若存在,请求出MO+MA的最小值;若不存在,请说明理由;
(3)如图2,若P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,设点P的横坐标为m,当m为何值时线段PD的长度最大,并求出最大值;
(4)如图3,若点E为抛物线的顶点,在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCE相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
浙江省2024年九年级上册精选期中考试模拟卷B
试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数一定是二次函数的是( )
A. B.y=3(x﹣1)2
C.y=ax2+bx+c D.y=2x+1
【分析】形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数叫做二次函数,其中x是自变量,a、b、c分别是函数表达式的二次项系数、一次项系数和常数项.据此解答即可.
【解答】解:根据二次函数的定义得:A、C、D不是二次函数,B是二次函数,
故选:B.
2.下列事件是必然事件的是( )
A.在足球赛中,弱队战胜强队
B.校园排球比赛,九年级一班获得冠军
C.从煮熟的鸡蛋里孵出小鸡
D.6月1日是儿童节
【分析】根据一定会发生的事件是必然事件逐项判断即可得出答案,
【解答】解:A.在足球赛中,弱队战胜强队是随机事件,故此选项不符合题意;
B.校园排球比赛,九年级一班获得冠军是随机事件,故此选项不符合题意,
C.从煮熟的鸡蛋里孵出小鸡是不可能事件,故此选项不符合题意,
D.6月1日是儿童节是必然事件,故此选项符合题意,
故选:D.
3.已知⊙O的半径为4,点P到圆心O的距离为4.8,则点P与⊙O的位置关系是( )
A.P在圆内 B.P在圆外 C.P在圆上 D.无法确定
【分析】通过比较点到圆心的距离d的距离与半径r的大小确定点与圆的位置关系,点到圆心的距离大于半径,得到点在圆外.
【解答】解:点P到圆心O的距离为4.8,⊙O的半径为4,
∵4.8>4,
∴点P在圆外.
故选:B.
4.a、b、c、d是成比例线段,其中a=6cm,b=3cm,c=4cm,则线段d的长可能为( )
A.2cm B.3cm C.4cm D.5cm
【分析】根据定义ad=cb,将a,b及c的值代入即可求得d.
【解答】解:∵a,b,c,d是成比例线段,a=6cm,b=3cm,c=4cm,
∴ad=bc,
∴d===2(cm).
故选:A.
5.某射击运动员在同一条件下的射击成绩记录如表:
射击次数 100 200 400 800 1000
“射中九环以上”的次数 87 172 336 679 850
“射中九环以上”的频率 0.87 0.86 0.84 0.85 0.85
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.84 B.0.85 C.0.86 D.0.87
【分析】根据大量的试验结果稳定在0.85即可得出结论.
【解答】解:根据表格知,从频率的波动情况可以发现频率稳定在0.85,
则该运动员“射中九环以上”的概率是0.85.
故选:B.
6.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么BF的长为( )
A. B. C. D.7
【分析】根据平行线分线段成比例定理判断即可.
【解答】解:∵AB∥CD∥EF,AC=2,AE=5,BD=1.5,
∴,
即=,
解得:,
故选:A.
7.把抛物线y=﹣2x2先向左平移3个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=﹣2(x+3)2+2 B.y=﹣2(x﹣3)2+2
C.y=﹣2(x+3)2﹣2 D.y=﹣2(x﹣3)2﹣2
【分析】按“上加下减,左加右减”的规律平移即可得出所求函数的解析式.
【解答】解:由上加下减,左加右减的法则可知,抛物线y=﹣2x2先向左平移3个单位,再向下平移2个单位后,得y=﹣2(x+3)2﹣2.
故选:C.
8.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为26cm,水面宽AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
【分析】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而得出CD的长即可.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵⊙O的直径为26cm,
∴OB=OC=13(cm),
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:C.
9.如图,在平面直角坐标系中,△DEF与△ABC位似,且原点O为位似中心,其位似比1:2,若点A(2,4),则其对应点D的坐标为( )
A.(1,2) B.(﹣1,﹣2) C. D.
【分析】由于位似的两个图形在原点的同侧,则A点的两个坐标分别乘即得D的坐标.
【解答】解:∵△DEF与△ABC位似,且原点O为位似中心,其位似比1:2,点A(2,4),
∴2×=1,4×=2,
∴其对应点D的坐标为(1,2),
故选:A.
10.如图,在矩形ABCD中,AB=8,AD=4,连结AC,E,F分别在边AD,CD上,连结BE,BF分别交AC于点M,N,若∠EBF=45°,CF=2,则下列结论中:①∠BEA+∠BFC=135°;②CA⊥BF;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据三角形内角和定理得△ABE与△BCF两个三角形所有内角相加为360°,结合矩形性质:每个内角都为90° 即可判断①;利用勾股定理求出AE,利用矩形的性质证明△ABN∽△CFN,利用相似三 角形相似比即可求出BN,从而判断③;利用矩形的性质及已知条件,由△ABN∽△CFN,得到∠CBN=∠BAC,进而说明∠BNC=90°,从而判断②.然后证明∠BMN=45°,得MN=BN,再证明△AEM∽△BCM,即可求得AM,进而求得AE,从而判断④.
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠BCD=90°,
∵∠EBF=45°,
∴∠ABE+∠CBF=45°,
∴∠BEA+∠BFC=135°,故①正确;
∵CF=2,BC=AD=4,
在Rt△CBF中,根据勾股定理得:BF===2,
∵CD∥AB,
∴△CFN∽△ABN,
∴=,
∵AB=CD=8,FN=BF﹣BN=2﹣BN,
∴=,
∴BN=,故③正确;
在Rt△ABC中,AC===4,
∵=,∠BCF=∠ABC=90°,
∴△BCF∽△ABC,
∴∠CBF=∠BAC,
∵∠BAC+∠ACB=90°,
∴∠CBF+∠ACB=90°,
∴∠CNB=90°,
∴CA⊥BF,故②正确;
∵∠EBF=45°,
∴∠BMN=45°,
∴MN=BN=,
∵∠CBF=∠BAC,∠BNC=∠ABC=90°,
∴△BCN∽△ABC,
∴==,
∴CN=BN=,
∴AM=AC﹣MN﹣CN=4﹣﹣=,CM=MN+CN=,
∵AD∥BC,
∴△AME∽△CBM,
∴=,
∴=,
∴AE=,故④错误,
∴结论正确的有①②③,共3个,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.抛物线y=(x﹣2)2的顶点坐标是 (2,0) .
【分析】因为顶点式y=a(x﹣h)2+k,顶点坐标是(h,k),对称轴是直线x=h.
【解答】解:因为抛物线y=(x﹣2)2是顶点式,
根据顶点式的坐标特点可知,顶点坐标是(2,0).
故答案为:(2,0).
12.若,则= .
【分析】设,得出a=3k,b=4k,c=5k,将其代入,即可求解.
【解答】解:设,
∴a=3k,b=4k,c=5k,
∴,
故答案为:.
13.从1﹣9的数字卡片中,任意抽一张,抽到奇数的可能性是 .
【分析】用奇数的个数除以总个数即可得出答案.
【解答】解:1﹣9的数字卡片中奇数有1,3,5,7,9,共5个数,
则抽到奇数的可能性是.
故答案为:.
14.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为 60° .
【分析】连接OC,OD,OE,由正六边形的性质得出∠COE=120°,由圆周角定理即可求解.
【解答】解:如图:连接OC,OD,OE,
∵多边形ABCDEF是正六边形,
∴,
∴∠COE=2∠COD=120°,
∴,
故答案为:60°.
15.如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为 4cm2 .
【分析】,BE=CE=4cm,即得△DEF∽△BAF,所以,即可求出,再由DG:GC=1:2可求得,由此即得答案.
【解答】解:如图所示,连接DE,
∵D、E分别为AC、BC中点,
∴DE∥AB,,,
∴△DEF∽△BAF,
∴,
∴,
∵∠ABC=90°,
∴∠DEC=90°,
∴,
∴,
∵DG:GC=1:2,
∴,
∴,
∴四边形DFEG的面积=.
故答案为:4cm2.
16.二次函数y=ax2+bx+c的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,﹣2<x1<﹣1,0<x2<1.下列结论中:
①4a﹣2b+c<0;②2a﹣b<0;③b<﹣1;④;⑤(a+c)2<b2.
正确的有 ①②③⑤ (写出所有正确结论的序号).
【分析】首先根据抛物线的开口方向可得到a<0,抛物线交y轴于正半轴,则c>0,而抛物线与x轴的交点中,﹣2<x1<﹣1、0<x2<1说明抛物线的对称轴在﹣1~0之间,即x=﹣>﹣1,可根据这些条件以及函数图象上一些特殊点的坐标来进行判断.
【解答】解:抛物线的开口向下,则a<0;抛物线的对称轴x=﹣>﹣1,且c>0;
①由图可得:当x=﹣2时,y<0,即4a﹣2b+c<0,故①正确;
②已知x=﹣>﹣1,且a<0,所以2a﹣b<0,故②正确;
③已知抛物线经过(﹣1,2),即a﹣b+c=2(1),
由图知:当x=1时,y<0,即a+b+c<0(2),
由(2)﹣(1)可得2b<﹣2,
∴b<﹣1,
故③正确;
④已知抛物线经过(﹣1,2),即a﹣b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),
由①知:4a﹣2b+c<0(3);
联立(1)(2),得:a+c<1;
联立(1)(3)得:2a﹣c<﹣4;
故3a<﹣3,即a<﹣1;
所以④错误;
⑤已知抛物线经过(﹣1,2),即a﹣b+c=2,
∴a+c=b+2,
∴(a+c)2=(2+b)2,
∵(2+b)2=4+4b+b2,
∵b<﹣1
∴4+4b=4(1+b)<0,
∴4+4b+b2<b2,
∴(a+c)2<b2,故⑤正确;
因此正确的结论是①②③⑤.
故答案为:①②③⑤.
三.解答题(共8小题,满分72分)
17.(6分)某数学兴趣小组测量校园内一棵树的高度.采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A.再用皮尺分别测量BF,DF,EF,观测者目高(CD)的长.利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D,EF⊥BD于点F.AB⊥BD于点B,BF=6米,DF=2米.EF=0.55米,CD=1.65米,求这棵树的高度(AB的长).
【分析】过点E作水平线交AB于点G,交CD于点H,根据镜面反射的性质求出△CHE∽△AGE,再根据对应边成比例解答即可.
【解答】解:过点E作水平线交AB于点G,交CD于点H,如图,
∵DB是水平线,CD,EF,AB都是铅垂线,
∴DH=EF=GB=0.55米,EH=DF=2米,EG=FB=6米,
∴CH=CD﹣DH=1.65﹣0.55=1.1(米),
又根据题意,得∠CHE=∠AGE=90°,∠CEH=∠AEG,
∴△CHE∽△AGE,
∴,即 ,
解得:AG=3.3米,
∴AB=AG+GB=3.3+0.55=3.85(米),
答:这棵树的高度为3.85米.
18.(8分)学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)在扇形统计图中,a= 15 ,b= 60 ,C类的圆心角为 54° ;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用列表法或画树状图的方法求出全是B类学生的概率.
【分析】(1)由A类人数及其所占百分比可得总人数;
(2)总人数减去A、B的人数求得C类人数,由360°乘以C类所占比例得C类的圆心角度数,用B的人数除以总人数可得对应百分比;
(3)列表得出所有等可能结果,再根据概率公式求解可得.
【解答】解:(1)全班学生总人数为:10÷25%=40(人);
(2)∵B类百分比为×100%=60%,
∴b=60,
∵C类人数为:40﹣(10+24)=6(人),
∴C类百分比为×100%=15%,
∴a=15,
∴C类的圆心角为360°×15%=54°,
故答案为:15,60,54°;
(3)列表如下:
A B B C
A / BA BA CA
B AB / BB CB
B AB BB / CB
C AC BC BC /
由表可知,共有12种等可能结果,其中全是B类学生的有2种结果,
∴P(全是B类学生)=.
19.(8分)如图,在△ABC中,BC的垂直平分线分别交BC、AC于点D、E,BE交AD于点F,且AB=AD.
(1)求证:△FDB∽△ABC;
(2)求的值.
【分析】(1)首先根据垂直平分线的性质可得BE=CE,进而可得∠FBD=∠C,再利用等腰三角形“等边对等角”的性质可得∠FDB=∠ABC,然后利用“两角对应相等,两个三角形相似”证明结论即可;
(2)首先解得,然后利用“相似三角形的面积比等于相似比的平方”,求解即可.
【解答】(1)证明:∵DE为线段BC的垂直平分线,
∴BE=CE,
∴∠FBD=∠C,
∵AB=AD,
∴∠FDB=∠ABC,
∴△FDB∽△ABC;
(2)解:∵DE为线段BC的垂直平分线,
∴,
∴,
由(1)可知,△FDB∽△ABC,
∴.
20.(8分)如图,△ABC中,AB=AC,∠BAC=42°,D为△ABC内一点,连接AD,将AD绕点A逆时针旋转42°,得到AE,连接DE,BD,CE.
(1)求证:BD=CE;
(2)若DE⊥AC,求∠BAD的度数.
【分析】(1)根据旋转的性质得到AD=AE,∠DAE=42°,求得∠CAE=∠BAD,根据全等三角形的性质得到BD=CE;
(2)根据等腰三角形的性质得到∠CAE=DAE=21°,根据全等三角形的性质得到结论.
【解答】(1)证明:∵将AD绕点A逆时针旋转42°,得到AE,
∴AD=AE,∠DAE=42°,
∵∠BAC=42°,
∴∠BAC=∠DAE,
∴∠CAE=∠BAD,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)解:由(1)知AD=AE,∠DAE=42°,
∵DE⊥AC,
∴∠CAE=DAE=21°,
∵∠BAD=∠CAE,
∴∠BAD=21°.
21.(10分)如图,A、B为一次函数y=﹣x+5的图象与二次函数y=x2+bx+c的图象的公共点,点A、B的横坐标分别为0、4.P为二次函数y=x2+bx+c的图象上的动点,且位于直线AB的下方,连接PA、PB.
(1)求b、c的值;
(2)求△PAB的面积的最大值.
【分析】(1)先求出A,B的坐标,再用待定系数法求出b,c;
(2)由(1)可得:y=x2﹣5x+5,设P(m,m2﹣5m+5),作PC∥OA,交AB于E,则E(m,﹣m+5),则PE=4m﹣m2,得出面积,即可解答.
【解答】解:(1)当x=0时,y=﹣x+5=5;当x=4时,y=﹣x+5=1,则A(0,5),B(4,1),
则,
解得:;
(2)由(1)可得:y=x2﹣5x+5,设P(m,m2﹣5m+5),作PE∥OA,交AB于E,
则E(m,﹣m+5),则PE=4m﹣m2,
∴,
当m=2时,最大值为8.
22.(10分)某超市销售某种商品,每件商品进价为40元,当每件售价为50元时,每天能售出500件,经市场调查表明:若售价每提高1元,日销售量就要少售出10件.
(1)若售价每提高x元,则日销售量为 (500﹣10x) 件.设每天利润为y元,则y与x的关系式是 y=﹣10x2+400x+5000 .
(2)要使日利润达到8750元,且尽量让消费者得到实惠,求每件售价应定为多少元?
【分析】(1)由每天能售出500件,若售价每提高1元,日销售量就要少售出10件,即可推到出答案;由总利润=销售数量×单个利润即可求解;
(2)令y=8750,代入(1)中函数关系式求解即可.
【解答】解:(1)设每天利润为y元,则y与x的关系式是y=(50+x﹣40)(500﹣x)=﹣10x2+40x+5000,
故答案为:(500﹣10x);y=﹣10x2+400x+5000;
(2)令y=8750,则﹣10x2+400x+5000=8750,
解得x1=15,x2=25,
∵尽量让消费者得到实惠,
∴x=15,
∴每件售价应定为50+15=65元.
23.(10分)如图,AB是⊙O的直径,D为AB上一点,C为⊙O上一点,且AD=AC,延长CD交⊙O于E,连CB.
(1)求证:∠CAB=2∠BCD;
(2)若∠BCE=15°,AB=6,求CE的长.
【分析】(1)根据圆周角定理得到∠ACB=90°,则∠ACD=90°﹣∠BCD,再利用等腰三角形的性质和三角形内角和得到∠A+90°﹣∠BCD+90°﹣∠BCD=180°,从而得到结论;
(2)连接OC、OE,如图,利用(1)的结论和圆周角定理得到∠A=∠BOE=30°,则∠COB=60°,所以∠COE=90°,然后利用勾股定理计算CE的长.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD=90°﹣∠BCD,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠A+∠ACD+∠ADC=180°,
∴∠A+90°﹣∠BCD+90°﹣∠BCD=180°,
∴∠A=2∠BCD;
(2)解:连接OC、OE,如图,
由(1)得∠A=2∠BCE=2×15°=30°,
∵∠BOE=2∠BCE=2×15°=30°,
∵OA=OC,
∴∠A=∠ACO,
∴∠COB=∠A+∠ACO=2∠A=60°,
∵∠COE=∠COB+∠BOE=60°+30°=90°,
而,
∴.
24.(12分)如图1,抛物线y=ax2+2x+c交x轴于A,B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上是否存在一点M,使得MO+MA的值最小,若存在,请求出MO+MA的最小值;若不存在,请说明理由;
(3)如图2,若P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,设点P的横坐标为m,当m为何值时线段PD的长度最大,并求出最大值;
(4)如图3,若点E为抛物线的顶点,在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCE相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
【分析】(1)求出B(3,0),C(0,3),用待定系数法可得抛物线的表达式为y=﹣x2+2x+3;
(2)作O关于直线BC的对称点K,可知MO+MA=MK+MA,当A,M,K共线时,MO+MA最小,最小值为AK的长,因∠OBC=45°,故K(3,3),可得AK==5,从而知MO+MA的最小值为5;
(3)根据PD∥y轴,点P的横坐标为m,有PD=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,根据二次函数性质可得答案;
(4)求出抛物线顶点E(1,4),由勾股定理逆定理可知△BCE是直角边的比为的直角三角形,若以A,C,Q为顶点的三角形与△BCE相似,则△ACQ也是直角边的比为的直角三角形,①若Q为直角顶点,由A(﹣1,0),C(0,3)知,Q(0,0);②若C为直角顶点,可求出CQ=3,AQ==10,得Q(9,0).
【解答】解:(1)在y=﹣x+3中,令x=0得y=3,令y=0得x=3,
∴B(3,0),C(0,3),
把B(3,0),C(0,3)代入y=ax2+2x+c得:
,
解得,
∴抛物线的表达式为y=﹣x2+2x+3;
(2)在直线BC上存在一点M,使得MO+MA的值最小,理由如下:
作O关于直线BC的对称点K,如图:
∴MO=MK,
∴MO+MA=MK+MA,
∴当A,M,K共线时,MO+MA最小,最小值为AK的长,
由B(3,0),C(0,3)知∠OBC=45°,
∵O,K关于直线BC对称,
∴∠KBC=∠OBC=45°,OB=KB=3,
∴∠OBK=90°,
∴K(3,3),
在y=﹣x2+2x+3中,令y=0得0=﹣x2+2x+3,
解得x=﹣1或x=3,
∴A(﹣1,0),
∴AK==5,
∴MO+MA的最小值为5;
(3)∵PD∥y轴,点P的横坐标为m,
∴P(m,﹣m+3),D(m,﹣m2+2m+3),
∴PD=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,
∵﹣1<0,
∴当m=时,线段PD取最大值;
(4)在x轴上存在一点Q,使得以A,C,Q为顶点的三角形与△BCE相似,理由如下:
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线顶点E(1,4),
∵B(3,0),C(0,3),
∴BC2=18,BE2=20,CE2=2,
∴BC2+CE2=BE2,==,
∴△BCE是直角边的比为的直角三角形,
若以A,C,Q为顶点的三角形与△BCE相似,则△ACQ也是直角边的比为的直角三角形,
①若Q为直角顶点,由A(﹣1,0),C(0,3)知,Q与O重合时,△COA∽△BCE,此时Q(0,0);
②若C为直角顶点,如图:
∵A(﹣1,0),C(0,3),
∴AC=,
∵=,
∴CQ=3,
∴AQ==10,
∴OQ=AQ﹣OA=10﹣1=9,
∴Q(9,0);
综上所述,Q的坐标为(0,0)或(9,0).
浙江省2024年九年级上册精选期中考试模拟卷B
满分:120分 范围:第1-4章
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数一定是二次函数的是( )
A. B.y=3(x﹣1)2
C.y=ax2+bx+c D.y=2x+1
2.下列事件是必然事件的是( )
A.在足球赛中,弱队战胜强队 B.校园排球比赛,九年级一班获得冠军
C.从煮熟的鸡蛋里孵出小鸡 D.6月1日是儿童节
3.已知⊙O的半径为4,点P到圆心O的距离为4.8,则点P与⊙O的位置关系是( )
A.P在圆内 B.P在圆外 C.P在圆上 D.无法确定
4.a、b、c、d是成比例线段,其中a=6cm,b=3cm,c=4cm,则线段d的长可能为( )
A.2cm B.3cm C.4cm D.5cm
5.某射击运动员在同一条件下的射击成绩记录如表:
射击次数 100 200 400 800 1000
“射中九环以上”的次数 87 172 336 679 850
“射中九环以上”的频率 0.87 0.86 0.84 0.85 0.85
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.84 B.0.85 C.0.86 D.0.87
6.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么BF的长为( )
A. B. C. D.7
7.把抛物线y=﹣2x2先向左平移3个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=﹣2(x+3)2+2 B.y=﹣2(x﹣3)2+2
C.y=﹣2(x+3)2﹣2 D.y=﹣2(x﹣3)2﹣2
8.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为26cm,水面宽AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
9.如图,在平面直角坐标系中,△DEF与△ABC位似,且原点O为位似中心,其位似比1:2,若点A(2,4),则其对应点D的坐标为( )
A.(1,2) B.(﹣1,﹣2) C. D.
10.如图,在矩形ABCD中,AB=8,AD=4,连结AC,E,F分别在边AD,CD上,连结BE,BF分别交AC于点M,N,若∠EBF=45°,CF=2,则下列结论中:①∠BEA+∠BFC=135°;②CA⊥BF;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.抛物线y=(x﹣2)2的顶点坐标是 .
12.若,则= .
13.从1﹣9的数字卡片中,任意抽一张,抽到奇数的可能性是 .
14.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为 .
15.如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为 .
16.二次函数y=ax2+bx+c的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,﹣2<x1<﹣1,0<x2<1.下列结论中:①4a﹣2b+c<0;②2a﹣b<0;③b<﹣1;④;⑤(a+c)2<b2.
正确的有 (写出所有正确结论的序号).
三.解答题(共8小题,满分72分)
17.(6分)某数学兴趣小组测量校园内一棵树的高度.采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A.再用皮尺分别测量BF,DF,EF,观测者目高(CD)的长.利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D,EF⊥BD于点F.AB⊥BD于点B,BF=6米,DF=2米.EF=0.55米,CD=1.65米,求这棵树的高度(AB的长).
18.(8分)学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)在扇形统计图中,a= ,b= ,C类的圆心角为 ;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用列表法或画树状图的方法求出全是B类学生的概率.
19.(8分)如图,在△ABC中,BC的垂直平分线分别交BC、AC于点D、E,BE交AD于点F,且AB=AD.
(1)求证:△FDB∽△ABC;
(2)求的值.
20.(8分)如图,△ABC中,AB=AC,∠BAC=42°,D为△ABC内一点,连接AD,将AD绕点A逆时针旋转42°,得到AE,连接DE,BD,CE.
(1)求证:BD=CE;
(2)若DE⊥AC,求∠BAD的度数.
21.(10分)如图,A、B为一次函数y=﹣x+5的图象与二次函数y=x2+bx+c的图象的公共点,点A、B的横坐标分别为0、4.P为二次函数y=x2+bx+c的图象上的动点,且位于直线AB的下方,连接PA、PB.
(1)求b、c的值;
(2)求△PAB的面积的最大值.
22.(10分)某超市销售某种商品,每件商品进价为40元,当每件售价为50元时,每天能售出500件,经市场调查表明:若售价每提高1元,日销售量就要少售出10件.
(1)若售价每提高x元,则日销售量为 件.设每天利润为y元,则y与x的关系式是 .
(2)要使日利润达到8750元,且尽量让消费者得到实惠,求每件售价应定为多少元?
23.(10分)如图,AB是⊙O的直径,D为AB上一点,C为⊙O上一点,且AD=AC,延长CD交⊙O于E,连CB.
(1)求证:∠CAB=2∠BCD;
(2)若∠BCE=15°,AB=6,求CE的长.
24.(12分)如图1,抛物线y=ax2+2x+c交x轴于A,B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上是否存在一点M,使得MO+MA的值最小,若存在,请求出MO+MA的最小值;若不存在,请说明理由;
(3)如图2,若P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,设点P的横坐标为m,当m为何值时线段PD的长度最大,并求出最大值;
(4)如图3,若点E为抛物线的顶点,在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCE相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
浙江省2024年九年级上册精选期中考试模拟卷B
试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数一定是二次函数的是( )
A. B.y=3(x﹣1)2
C.y=ax2+bx+c D.y=2x+1
【分析】形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数叫做二次函数,其中x是自变量,a、b、c分别是函数表达式的二次项系数、一次项系数和常数项.据此解答即可.
【解答】解:根据二次函数的定义得:A、C、D不是二次函数,B是二次函数,
故选:B.
2.下列事件是必然事件的是( )
A.在足球赛中,弱队战胜强队
B.校园排球比赛,九年级一班获得冠军
C.从煮熟的鸡蛋里孵出小鸡
D.6月1日是儿童节
【分析】根据一定会发生的事件是必然事件逐项判断即可得出答案,
【解答】解:A.在足球赛中,弱队战胜强队是随机事件,故此选项不符合题意;
B.校园排球比赛,九年级一班获得冠军是随机事件,故此选项不符合题意,
C.从煮熟的鸡蛋里孵出小鸡是不可能事件,故此选项不符合题意,
D.6月1日是儿童节是必然事件,故此选项符合题意,
故选:D.
3.已知⊙O的半径为4,点P到圆心O的距离为4.8,则点P与⊙O的位置关系是( )
A.P在圆内 B.P在圆外 C.P在圆上 D.无法确定
【分析】通过比较点到圆心的距离d的距离与半径r的大小确定点与圆的位置关系,点到圆心的距离大于半径,得到点在圆外.
【解答】解:点P到圆心O的距离为4.8,⊙O的半径为4,
∵4.8>4,
∴点P在圆外.
故选:B.
4.a、b、c、d是成比例线段,其中a=6cm,b=3cm,c=4cm,则线段d的长可能为( )
A.2cm B.3cm C.4cm D.5cm
【分析】根据定义ad=cb,将a,b及c的值代入即可求得d.
【解答】解:∵a,b,c,d是成比例线段,a=6cm,b=3cm,c=4cm,
∴ad=bc,
∴d===2(cm).
故选:A.
5.某射击运动员在同一条件下的射击成绩记录如表:
射击次数 100 200 400 800 1000
“射中九环以上”的次数 87 172 336 679 850
“射中九环以上”的频率 0.87 0.86 0.84 0.85 0.85
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.84 B.0.85 C.0.86 D.0.87
【分析】根据大量的试验结果稳定在0.85即可得出结论.
【解答】解:根据表格知,从频率的波动情况可以发现频率稳定在0.85,
则该运动员“射中九环以上”的概率是0.85.
故选:B.
6.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么BF的长为( )
A. B. C. D.7
【分析】根据平行线分线段成比例定理判断即可.
【解答】解:∵AB∥CD∥EF,AC=2,AE=5,BD=1.5,
∴,
即=,
解得:,
故选:A.
7.把抛物线y=﹣2x2先向左平移3个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=﹣2(x+3)2+2 B.y=﹣2(x﹣3)2+2
C.y=﹣2(x+3)2﹣2 D.y=﹣2(x﹣3)2﹣2
【分析】按“上加下减,左加右减”的规律平移即可得出所求函数的解析式.
【解答】解:由上加下减,左加右减的法则可知,抛物线y=﹣2x2先向左平移3个单位,再向下平移2个单位后,得y=﹣2(x+3)2﹣2.
故选:C.
8.如图所示一个圆柱体容器内装入一些水,截面AB在圆心O下方,若⊙O的直径为26cm,水面宽AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
【分析】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而得出CD的长即可.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵⊙O的直径为26cm,
∴OB=OC=13(cm),
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:C.
9.如图,在平面直角坐标系中,△DEF与△ABC位似,且原点O为位似中心,其位似比1:2,若点A(2,4),则其对应点D的坐标为( )
A.(1,2) B.(﹣1,﹣2) C. D.
【分析】由于位似的两个图形在原点的同侧,则A点的两个坐标分别乘即得D的坐标.
【解答】解:∵△DEF与△ABC位似,且原点O为位似中心,其位似比1:2,点A(2,4),
∴2×=1,4×=2,
∴其对应点D的坐标为(1,2),
故选:A.
10.如图,在矩形ABCD中,AB=8,AD=4,连结AC,E,F分别在边AD,CD上,连结BE,BF分别交AC于点M,N,若∠EBF=45°,CF=2,则下列结论中:①∠BEA+∠BFC=135°;②CA⊥BF;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据三角形内角和定理得△ABE与△BCF两个三角形所有内角相加为360°,结合矩形性质:每个内角都为90° 即可判断①;利用勾股定理求出AE,利用矩形的性质证明△ABN∽△CFN,利用相似三 角形相似比即可求出BN,从而判断③;利用矩形的性质及已知条件,由△ABN∽△CFN,得到∠CBN=∠BAC,进而说明∠BNC=90°,从而判断②.然后证明∠BMN=45°,得MN=BN,再证明△AEM∽△BCM,即可求得AM,进而求得AE,从而判断④.
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠BCD=90°,
∵∠EBF=45°,
∴∠ABE+∠CBF=45°,
∴∠BEA+∠BFC=135°,故①正确;
∵CF=2,BC=AD=4,
在Rt△CBF中,根据勾股定理得:BF===2,
∵CD∥AB,
∴△CFN∽△ABN,
∴=,
∵AB=CD=8,FN=BF﹣BN=2﹣BN,
∴=,
∴BN=,故③正确;
在Rt△ABC中,AC===4,
∵=,∠BCF=∠ABC=90°,
∴△BCF∽△ABC,
∴∠CBF=∠BAC,
∵∠BAC+∠ACB=90°,
∴∠CBF+∠ACB=90°,
∴∠CNB=90°,
∴CA⊥BF,故②正确;
∵∠EBF=45°,
∴∠BMN=45°,
∴MN=BN=,
∵∠CBF=∠BAC,∠BNC=∠ABC=90°,
∴△BCN∽△ABC,
∴==,
∴CN=BN=,
∴AM=AC﹣MN﹣CN=4﹣﹣=,CM=MN+CN=,
∵AD∥BC,
∴△AME∽△CBM,
∴=,
∴=,
∴AE=,故④错误,
∴结论正确的有①②③,共3个,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.抛物线y=(x﹣2)2的顶点坐标是 (2,0) .
【分析】因为顶点式y=a(x﹣h)2+k,顶点坐标是(h,k),对称轴是直线x=h.
【解答】解:因为抛物线y=(x﹣2)2是顶点式,
根据顶点式的坐标特点可知,顶点坐标是(2,0).
故答案为:(2,0).
12.若,则= .
【分析】设,得出a=3k,b=4k,c=5k,将其代入,即可求解.
【解答】解:设,
∴a=3k,b=4k,c=5k,
∴,
故答案为:.
13.从1﹣9的数字卡片中,任意抽一张,抽到奇数的可能性是 .
【分析】用奇数的个数除以总个数即可得出答案.
【解答】解:1﹣9的数字卡片中奇数有1,3,5,7,9,共5个数,
则抽到奇数的可能性是.
故答案为:.
14.如图,正六边形ABCDEF内接于⊙O,点M在上,则∠CME的度数为 60° .
【分析】连接OC,OD,OE,由正六边形的性质得出∠COE=120°,由圆周角定理即可求解.
【解答】解:如图:连接OC,OD,OE,
∵多边形ABCDEF是正六边形,
∴,
∴∠COE=2∠COD=120°,
∴,
故答案为:60°.
15.如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为 4cm2 .
【分析】,BE=CE=4cm,即得△DEF∽△BAF,所以,即可求出,再由DG:GC=1:2可求得,由此即得答案.
【解答】解:如图所示,连接DE,
∵D、E分别为AC、BC中点,
∴DE∥AB,,,
∴△DEF∽△BAF,
∴,
∴,
∵∠ABC=90°,
∴∠DEC=90°,
∴,
∴,
∵DG:GC=1:2,
∴,
∴,
∴四边形DFEG的面积=.
故答案为:4cm2.
16.二次函数y=ax2+bx+c的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,x2,﹣2<x1<﹣1,0<x2<1.下列结论中:
①4a﹣2b+c<0;②2a﹣b<0;③b<﹣1;④;⑤(a+c)2<b2.
正确的有 ①②③⑤ (写出所有正确结论的序号).
【分析】首先根据抛物线的开口方向可得到a<0,抛物线交y轴于正半轴,则c>0,而抛物线与x轴的交点中,﹣2<x1<﹣1、0<x2<1说明抛物线的对称轴在﹣1~0之间,即x=﹣>﹣1,可根据这些条件以及函数图象上一些特殊点的坐标来进行判断.
【解答】解:抛物线的开口向下,则a<0;抛物线的对称轴x=﹣>﹣1,且c>0;
①由图可得:当x=﹣2时,y<0,即4a﹣2b+c<0,故①正确;
②已知x=﹣>﹣1,且a<0,所以2a﹣b<0,故②正确;
③已知抛物线经过(﹣1,2),即a﹣b+c=2(1),
由图知:当x=1时,y<0,即a+b+c<0(2),
由(2)﹣(1)可得2b<﹣2,
∴b<﹣1,
故③正确;
④已知抛物线经过(﹣1,2),即a﹣b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),
由①知:4a﹣2b+c<0(3);
联立(1)(2),得:a+c<1;
联立(1)(3)得:2a﹣c<﹣4;
故3a<﹣3,即a<﹣1;
所以④错误;
⑤已知抛物线经过(﹣1,2),即a﹣b+c=2,
∴a+c=b+2,
∴(a+c)2=(2+b)2,
∵(2+b)2=4+4b+b2,
∵b<﹣1
∴4+4b=4(1+b)<0,
∴4+4b+b2<b2,
∴(a+c)2<b2,故⑤正确;
因此正确的结论是①②③⑤.
故答案为:①②③⑤.
三.解答题(共8小题,满分72分)
17.(6分)某数学兴趣小组测量校园内一棵树的高度.采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A.再用皮尺分别测量BF,DF,EF,观测者目高(CD)的长.利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D,EF⊥BD于点F.AB⊥BD于点B,BF=6米,DF=2米.EF=0.55米,CD=1.65米,求这棵树的高度(AB的长).
【分析】过点E作水平线交AB于点G,交CD于点H,根据镜面反射的性质求出△CHE∽△AGE,再根据对应边成比例解答即可.
【解答】解:过点E作水平线交AB于点G,交CD于点H,如图,
∵DB是水平线,CD,EF,AB都是铅垂线,
∴DH=EF=GB=0.55米,EH=DF=2米,EG=FB=6米,
∴CH=CD﹣DH=1.65﹣0.55=1.1(米),
又根据题意,得∠CHE=∠AGE=90°,∠CEH=∠AEG,
∴△CHE∽△AGE,
∴,即 ,
解得:AG=3.3米,
∴AB=AG+GB=3.3+0.55=3.85(米),
答:这棵树的高度为3.85米.
18.(8分)学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
(1)求全班学生总人数;
(2)在扇形统计图中,a= 15 ,b= 60 ,C类的圆心角为 54° ;
(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用列表法或画树状图的方法求出全是B类学生的概率.
【分析】(1)由A类人数及其所占百分比可得总人数;
(2)总人数减去A、B的人数求得C类人数,由360°乘以C类所占比例得C类的圆心角度数,用B的人数除以总人数可得对应百分比;
(3)列表得出所有等可能结果,再根据概率公式求解可得.
【解答】解:(1)全班学生总人数为:10÷25%=40(人);
(2)∵B类百分比为×100%=60%,
∴b=60,
∵C类人数为:40﹣(10+24)=6(人),
∴C类百分比为×100%=15%,
∴a=15,
∴C类的圆心角为360°×15%=54°,
故答案为:15,60,54°;
(3)列表如下:
A B B C
A / BA BA CA
B AB / BB CB
B AB BB / CB
C AC BC BC /
由表可知,共有12种等可能结果,其中全是B类学生的有2种结果,
∴P(全是B类学生)=.
19.(8分)如图,在△ABC中,BC的垂直平分线分别交BC、AC于点D、E,BE交AD于点F,且AB=AD.
(1)求证:△FDB∽△ABC;
(2)求的值.
【分析】(1)首先根据垂直平分线的性质可得BE=CE,进而可得∠FBD=∠C,再利用等腰三角形“等边对等角”的性质可得∠FDB=∠ABC,然后利用“两角对应相等,两个三角形相似”证明结论即可;
(2)首先解得,然后利用“相似三角形的面积比等于相似比的平方”,求解即可.
【解答】(1)证明:∵DE为线段BC的垂直平分线,
∴BE=CE,
∴∠FBD=∠C,
∵AB=AD,
∴∠FDB=∠ABC,
∴△FDB∽△ABC;
(2)解:∵DE为线段BC的垂直平分线,
∴,
∴,
由(1)可知,△FDB∽△ABC,
∴.
20.(8分)如图,△ABC中,AB=AC,∠BAC=42°,D为△ABC内一点,连接AD,将AD绕点A逆时针旋转42°,得到AE,连接DE,BD,CE.
(1)求证:BD=CE;
(2)若DE⊥AC,求∠BAD的度数.
【分析】(1)根据旋转的性质得到AD=AE,∠DAE=42°,求得∠CAE=∠BAD,根据全等三角形的性质得到BD=CE;
(2)根据等腰三角形的性质得到∠CAE=DAE=21°,根据全等三角形的性质得到结论.
【解答】(1)证明:∵将AD绕点A逆时针旋转42°,得到AE,
∴AD=AE,∠DAE=42°,
∵∠BAC=42°,
∴∠BAC=∠DAE,
∴∠CAE=∠BAD,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)解:由(1)知AD=AE,∠DAE=42°,
∵DE⊥AC,
∴∠CAE=DAE=21°,
∵∠BAD=∠CAE,
∴∠BAD=21°.
21.(10分)如图,A、B为一次函数y=﹣x+5的图象与二次函数y=x2+bx+c的图象的公共点,点A、B的横坐标分别为0、4.P为二次函数y=x2+bx+c的图象上的动点,且位于直线AB的下方,连接PA、PB.
(1)求b、c的值;
(2)求△PAB的面积的最大值.
【分析】(1)先求出A,B的坐标,再用待定系数法求出b,c;
(2)由(1)可得:y=x2﹣5x+5,设P(m,m2﹣5m+5),作PC∥OA,交AB于E,则E(m,﹣m+5),则PE=4m﹣m2,得出面积,即可解答.
【解答】解:(1)当x=0时,y=﹣x+5=5;当x=4时,y=﹣x+5=1,则A(0,5),B(4,1),
则,
解得:;
(2)由(1)可得:y=x2﹣5x+5,设P(m,m2﹣5m+5),作PE∥OA,交AB于E,
则E(m,﹣m+5),则PE=4m﹣m2,
∴,
当m=2时,最大值为8.
22.(10分)某超市销售某种商品,每件商品进价为40元,当每件售价为50元时,每天能售出500件,经市场调查表明:若售价每提高1元,日销售量就要少售出10件.
(1)若售价每提高x元,则日销售量为 (500﹣10x) 件.设每天利润为y元,则y与x的关系式是 y=﹣10x2+400x+5000 .
(2)要使日利润达到8750元,且尽量让消费者得到实惠,求每件售价应定为多少元?
【分析】(1)由每天能售出500件,若售价每提高1元,日销售量就要少售出10件,即可推到出答案;由总利润=销售数量×单个利润即可求解;
(2)令y=8750,代入(1)中函数关系式求解即可.
【解答】解:(1)设每天利润为y元,则y与x的关系式是y=(50+x﹣40)(500﹣x)=﹣10x2+40x+5000,
故答案为:(500﹣10x);y=﹣10x2+400x+5000;
(2)令y=8750,则﹣10x2+400x+5000=8750,
解得x1=15,x2=25,
∵尽量让消费者得到实惠,
∴x=15,
∴每件售价应定为50+15=65元.
23.(10分)如图,AB是⊙O的直径,D为AB上一点,C为⊙O上一点,且AD=AC,延长CD交⊙O于E,连CB.
(1)求证:∠CAB=2∠BCD;
(2)若∠BCE=15°,AB=6,求CE的长.
【分析】(1)根据圆周角定理得到∠ACB=90°,则∠ACD=90°﹣∠BCD,再利用等腰三角形的性质和三角形内角和得到∠A+90°﹣∠BCD+90°﹣∠BCD=180°,从而得到结论;
(2)连接OC、OE,如图,利用(1)的结论和圆周角定理得到∠A=∠BOE=30°,则∠COB=60°,所以∠COE=90°,然后利用勾股定理计算CE的长.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD=90°﹣∠BCD,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠A+∠ACD+∠ADC=180°,
∴∠A+90°﹣∠BCD+90°﹣∠BCD=180°,
∴∠A=2∠BCD;
(2)解:连接OC、OE,如图,
由(1)得∠A=2∠BCE=2×15°=30°,
∵∠BOE=2∠BCE=2×15°=30°,
∵OA=OC,
∴∠A=∠ACO,
∴∠COB=∠A+∠ACO=2∠A=60°,
∵∠COE=∠COB+∠BOE=60°+30°=90°,
而,
∴.
24.(12分)如图1,抛物线y=ax2+2x+c交x轴于A,B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上是否存在一点M,使得MO+MA的值最小,若存在,请求出MO+MA的最小值;若不存在,请说明理由;
(3)如图2,若P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,设点P的横坐标为m,当m为何值时线段PD的长度最大,并求出最大值;
(4)如图3,若点E为抛物线的顶点,在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCE相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
【分析】(1)求出B(3,0),C(0,3),用待定系数法可得抛物线的表达式为y=﹣x2+2x+3;
(2)作O关于直线BC的对称点K,可知MO+MA=MK+MA,当A,M,K共线时,MO+MA最小,最小值为AK的长,因∠OBC=45°,故K(3,3),可得AK==5,从而知MO+MA的最小值为5;
(3)根据PD∥y轴,点P的横坐标为m,有PD=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,根据二次函数性质可得答案;
(4)求出抛物线顶点E(1,4),由勾股定理逆定理可知△BCE是直角边的比为的直角三角形,若以A,C,Q为顶点的三角形与△BCE相似,则△ACQ也是直角边的比为的直角三角形,①若Q为直角顶点,由A(﹣1,0),C(0,3)知,Q(0,0);②若C为直角顶点,可求出CQ=3,AQ==10,得Q(9,0).
【解答】解:(1)在y=﹣x+3中,令x=0得y=3,令y=0得x=3,
∴B(3,0),C(0,3),
把B(3,0),C(0,3)代入y=ax2+2x+c得:
,
解得,
∴抛物线的表达式为y=﹣x2+2x+3;
(2)在直线BC上存在一点M,使得MO+MA的值最小,理由如下:
作O关于直线BC的对称点K,如图:
∴MO=MK,
∴MO+MA=MK+MA,
∴当A,M,K共线时,MO+MA最小,最小值为AK的长,
由B(3,0),C(0,3)知∠OBC=45°,
∵O,K关于直线BC对称,
∴∠KBC=∠OBC=45°,OB=KB=3,
∴∠OBK=90°,
∴K(3,3),
在y=﹣x2+2x+3中,令y=0得0=﹣x2+2x+3,
解得x=﹣1或x=3,
∴A(﹣1,0),
∴AK==5,
∴MO+MA的最小值为5;
(3)∵PD∥y轴,点P的横坐标为m,
∴P(m,﹣m+3),D(m,﹣m2+2m+3),
∴PD=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,
∵﹣1<0,
∴当m=时,线段PD取最大值;
(4)在x轴上存在一点Q,使得以A,C,Q为顶点的三角形与△BCE相似,理由如下:
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线顶点E(1,4),
∵B(3,0),C(0,3),
∴BC2=18,BE2=20,CE2=2,
∴BC2+CE2=BE2,==,
∴△BCE是直角边的比为的直角三角形,
若以A,C,Q为顶点的三角形与△BCE相似,则△ACQ也是直角边的比为的直角三角形,
①若Q为直角顶点,由A(﹣1,0),C(0,3)知,Q与O重合时,△COA∽△BCE,此时Q(0,0);
②若C为直角顶点,如图:
∵A(﹣1,0),C(0,3),
∴AC=,
∵=,
∴CQ=3,
∴AQ==10,
∴OQ=AQ﹣OA=10﹣1=9,
∴Q(9,0);
综上所述,Q的坐标为(0,0)或(9,0).
同课章节目录
