2016春北师大版九年级数学下册教学课件:1.4解直角三角形(共22张PPT)
文档属性
| 名称 | 2016春北师大版九年级数学下册教学课件:1.4解直角三角形(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-29 00:00:00 | ||
图片预览






文档简介
课件22张PPT。1.4 解直角三角形第一章 直角三角形的边角关系30°、45°、60°角的正弦值、余弦值和正切值如下表:对于sinα与tanα,角度越大,函数值也越大;(带正)
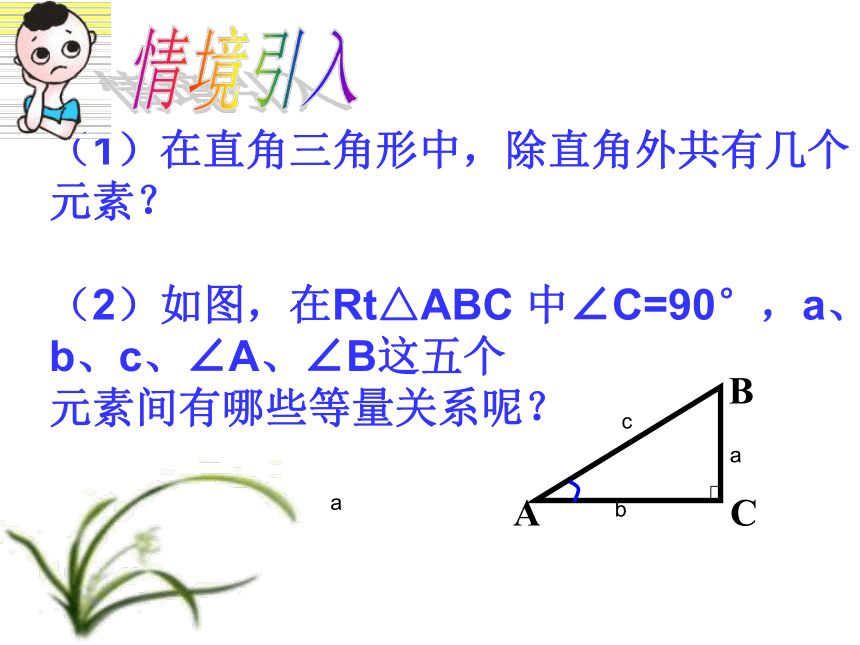
对于cosα,角度越大,函数值越小。知识回顾(1)在直角三角形中,除直角外共有几个 元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个
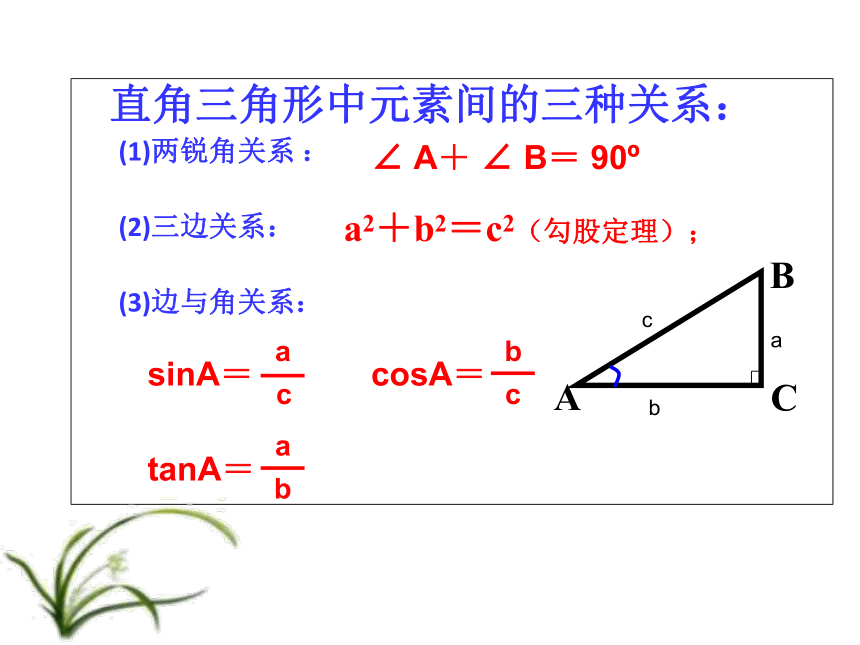
元素间有哪些等量关系呢? acba情境引入 直角三角形中元素间的三种关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
cbaa2+b2=c2(勾股定理);∠ A+ ∠ B= 90osinA=1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B(2)已知b=10,∠B=60°,求 ∠A ,a,c.(3)已知c=20,∠A=60°,求 ∠B, a,b. (4)已知a=1,b= ,求c, ∠A, ∠B
自主预习定义:
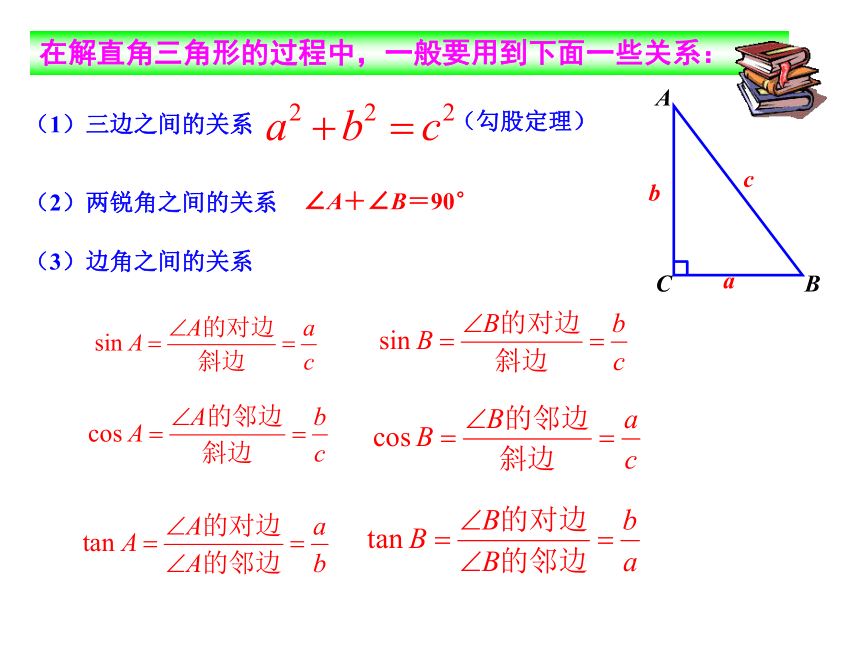
由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.新知探究事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.解直角三角形:在直角三角形中,由已知元素求未知元素的过程.在解直角三角形的过程中,一般要用到下面一些关系:解直角三角形(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 (勾股定理)在解直角三角形的过程中,一般要用到下面一些关系:
问题:1、解直角三角形需要什么条件?
议一议2、解直角三角形的条件可分为哪几类? 例1在探究一、已知两条边解直角三角形:中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=√15,b=5,求这个三角形的其他元素。
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形。探究二、
已知一条边和一个锐角 (两个已知元素中至少有一条边)解直角三角形:
例2,在中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°求这个三角形的其他元素(边长精确到1)。 1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
D2、在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 3 , b = 3 ;练习(2)c=8,∠A=60°(3)a=5,c=10.3.已知:在Rt△ABC中,∠C=90,b=2 、c=4.
求:(1)a、∠B=怎样思考?1、如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形。6随堂练习怎样思考?D3、如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.求:△ABC的面积(结果可保留根号). 怎样思考?3、已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,
若∠B=30°,CD=6,求AB的长.
怎样思考?中考点击
4、 如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。ABCD260°15. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.30AB的长D6、你能根据图上信息,提出一个用锐角三角函数解决的实际问题吗?试一试探索2、解直角三角形的条件可分为两大类:
①、已知一锐角、一边
(一锐角、一直角边或一斜边)
②、已知两边
(一直角边,一斜边或者两条直角边)1、解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)知识梳理
对于cosα,角度越大,函数值越小。知识回顾(1)在直角三角形中,除直角外共有几个 元素?
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个
元素间有哪些等量关系呢? acba情境引入 直角三角形中元素间的三种关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
cbaa2+b2=c2(勾股定理);∠ A+ ∠ B= 90osinA=1、在Rt△ABC中,∠C=90°:
(1)已知a=4,c=8,求b, ∠A ,∠B(2)已知b=10,∠B=60°,求 ∠A ,a,c.(3)已知c=20,∠A=60°,求 ∠B, a,b. (4)已知a=1,b= ,求c, ∠A, ∠B
自主预习定义:
由直角三角形中的已知元素,求出所有末知元素的过程,叫做解直角三角形.新知探究事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.解直角三角形:在直角三角形中,由已知元素求未知元素的过程.在解直角三角形的过程中,一般要用到下面一些关系:解直角三角形(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 (勾股定理)在解直角三角形的过程中,一般要用到下面一些关系:
问题:1、解直角三角形需要什么条件?
议一议2、解直角三角形的条件可分为哪几类? 例1在探究一、已知两条边解直角三角形:中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=√15,b=5,求这个三角形的其他元素。
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形。探究二、
已知一条边和一个锐角 (两个已知元素中至少有一条边)解直角三角形:
例2,在中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°求这个三角形的其他元素(边长精确到1)。 1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
D2、在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 3 , b = 3 ;练习(2)c=8,∠A=60°(3)a=5,c=10.3.已知:在Rt△ABC中,∠C=90,b=2 、c=4.
求:(1)a、∠B=怎样思考?1、如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形。6随堂练习怎样思考?D3、如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8.求:△ABC的面积(结果可保留根号). 怎样思考?3、已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,
若∠B=30°,CD=6,求AB的长.
怎样思考?中考点击
4、 如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。ABCD260°15. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.30AB的长D6、你能根据图上信息,提出一个用锐角三角函数解决的实际问题吗?试一试探索2、解直角三角形的条件可分为两大类:
①、已知一锐角、一边
(一锐角、一直角边或一斜边)
②、已知两边
(一直角边,一斜边或者两条直角边)1、解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边)知识梳理
