2024-2025学年山东省-淄博市淄博实验中学高三(上)月考数学试卷(10月份)(含答案)
文档属性
| 名称 | 2024-2025学年山东省-淄博市淄博实验中学高三(上)月考数学试卷(10月份)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 298.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览




文档简介
2024-2025学年山东省淄博实验中学高三(上)月考数学试卷(10月份)
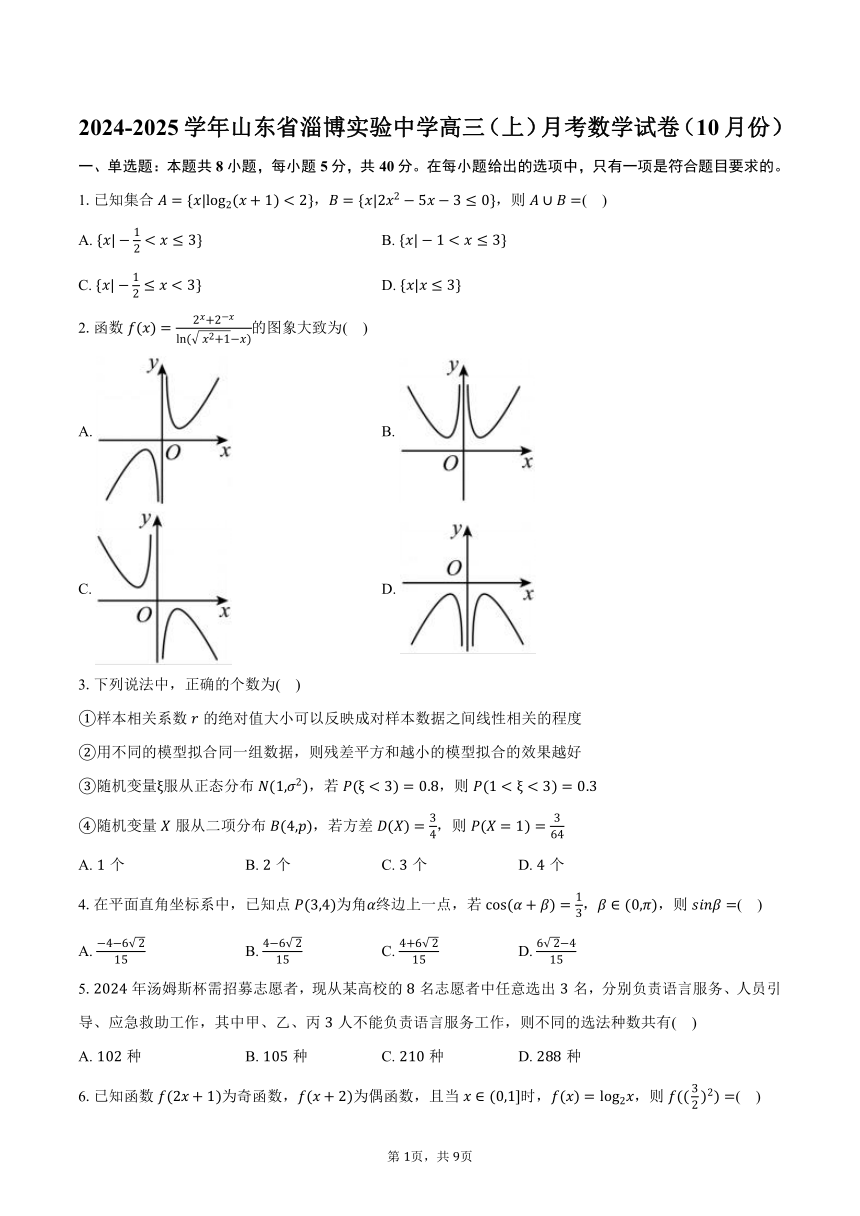
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B.
C. D.
2.函数的图象大致为( )
A. B.
C. D.
3.下列说法中,正确的个数为( )
样本相关系数的绝对值大小可以反映成对样本数据之间线性相关的程度
用不同的模型拟合同一组数据,则残差平方和越小的模型拟合的效果越好
随机变量服从正态分布,若,则
随机变量服从二项分布,若方差,则
A. 个 B. 个 C. 个 D. 个
4.在平面直角坐标系中,已知点为角终边上一点,若,,则( )
A. B. C. D.
5.年汤姆斯杯需招募志愿者,现从某高校的名志愿者中任意选出名,分别负责语言服务、人员引导、应急救助工作,其中甲、乙、丙人不能负责语言服务工作,则不同的选法种数共有( )
A. 种 B. 种 C. 种 D. 种
6.已知函数为奇函数,为偶函数,且当时,,则( )
A. B. C. D.
7.设,,,则下列关系正确的是( )
A. B. C. D.
8.若函数在上有个零点,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知,且,,则( )
A. B.
C. D.
10.已知定义在上的函数满足当时,,当时,满足,为常数,则下列叙述中正确的为( )
A. 当时,
B. 当时,的解析式为
C. 当时,在上恒成立
D. 当时,函数的图象与直线,在上的交点个数为
11.设数列满足,,记数列的前项和为,则( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.若的展开式中含的项的系数为,则的最小值为______.
13.已知:函数是定义在上的可导函数,当时,,若,且对任意,不等式恒成立,则实数的取值范围是______.
14.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字,,,,乙的卡片上分别标有数字,,,,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得分,数字小的人得分,然后各自弃置此轮所选的卡片弃置的卡片在此后轮次中不能使用则四轮比赛后,甲的总得分不小于的概率为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
设函数.
若,求函数的单调区间;
设函数在上有两个零点,求实数的取值范围其中是自然对数的底数
16.本小题分
记为数列的前项和,已知,.
求,并证明是等差数列;
求.
17.本小题分
如图,在四边形中,,,,.
求的大小;
求的面积的最大值;
若,求的面积.
18.本小题分
第十五届全国运动会将于年在广东、香港、澳门三地举办为了普及全运知识,某大学举办了一次全运知识闯关比赛,比赛分为初赛与复赛,初赛胜利后才能参加复赛,初赛规定:三人组队参赛,每次只派一个人,且每人只派一次;如果一个人闯关失败,再派下一个人重新闯关;三人中只要有人闯关成功即视作初赛胜利,无需继续闯关现有甲、乙、丙三人组队参加初赛,他们各自闯关成功的概率分别为、、,假定、、互不相等,且每人能否闯关成功相互独立.
若计划依次派甲、乙、丙进行初赛闯关,,求该小组初赛胜利的概率;
已知,若乙只能安排在第二个派出,要使初赛派出人员数目的期望较小,试确定甲、丙谁先派出;
初赛胜利小组的三名成员都可以进入复赛,复赛规定:单人参赛,每个人回答三道题,全部答对获得一等奖;答对两道题获得二等奖;答对一道题获得三等奖;全部答错不获奖,已知某学生进入了复赛,他在复赛中前两道题答对的概率均为,第三道题答对的概率为若他获得一等奖的概率为,设他获得二等奖的概率为,求的最小值.
19.本小题分
已知函数,其中是自然对数的底数.
当时,求在上的值域;
当时,讨论的零点个数;
当时,证明:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:当时,,的定义域为,
,
令,则,解得,
令,则,解得.
函数的单调递增区间为,单调递减区间为.
令,则.
令,其中,
则.
令,解得,令,解得.
的单调递减区间为,单调递增区间为,
.
又,函数在上有两个零点,
的取值范围是.
16.解:当时,,解得,
当时,,解得,
所以;
证明:由,得,则,
两式相减得,则,
令,则,,
所以是以为首项,以为公差的等差数列;
当为偶数时,
,
则.
17.解:在中,由正弦定理得,
因为,,所以,
因为,所以为锐角,可得,
所以;
在中,,
由余弦定理得,
整理得,当且仅当时取等号,
所以.
当时,的面积取得最大值;
因为,所以舍负.
可得.
在中,由正弦定理得,即,解得.
所以,即的面积为.
18.解:设事件表示该小组获胜,
则,
所以该小解组初赛胜利的概率为,
若依次派出甲乙丙进行闯关,设派出的人员数目为,
则的可能取值为,,,
则,
,
,
此时,
若依次派出丙乙甲进行闯关,设派出的人员数目为,
则的可能取值为,,,
则,
,
,
此时,
所以
,
因为,
所以,,
所以,
所以要使初赛派出人员数目的期望较小,先派出甲.
由题意可得,,
则,
令,
则,
令,
所以当时,,为减函数,
当时,,为增函数,
所以,
所以的最小值为.
19.解:当时,,,
,,
在上单调递减,
又,,
在上的值域为.
,
令得,
当时,,单调递减;
当时,,单调递增,
,
当时,,
,则在上有且仅有个零点;
当时,令,,
在上单调递增,
,即,又,
在上有个零点,又,
令,则,
在上单调递减,
,
,
在上有一个零点.
综上所述,时,有一个零点,
时,有个零点.
证明:当,时,,
设,
当时,,,
又由知,,
当时,,
设,则,
在单调递增,,
,即在单调递增,,
综上,,即当时,,
即.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B.
C. D.
2.函数的图象大致为( )
A. B.
C. D.
3.下列说法中,正确的个数为( )
样本相关系数的绝对值大小可以反映成对样本数据之间线性相关的程度
用不同的模型拟合同一组数据,则残差平方和越小的模型拟合的效果越好
随机变量服从正态分布,若,则
随机变量服从二项分布,若方差,则
A. 个 B. 个 C. 个 D. 个
4.在平面直角坐标系中,已知点为角终边上一点,若,,则( )
A. B. C. D.
5.年汤姆斯杯需招募志愿者,现从某高校的名志愿者中任意选出名,分别负责语言服务、人员引导、应急救助工作,其中甲、乙、丙人不能负责语言服务工作,则不同的选法种数共有( )
A. 种 B. 种 C. 种 D. 种
6.已知函数为奇函数,为偶函数,且当时,,则( )
A. B. C. D.
7.设,,,则下列关系正确的是( )
A. B. C. D.
8.若函数在上有个零点,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知,且,,则( )
A. B.
C. D.
10.已知定义在上的函数满足当时,,当时,满足,为常数,则下列叙述中正确的为( )
A. 当时,
B. 当时,的解析式为
C. 当时,在上恒成立
D. 当时,函数的图象与直线,在上的交点个数为
11.设数列满足,,记数列的前项和为,则( )
A. B.
C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.若的展开式中含的项的系数为,则的最小值为______.
13.已知:函数是定义在上的可导函数,当时,,若,且对任意,不等式恒成立,则实数的取值范围是______.
14.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字,,,,乙的卡片上分别标有数字,,,,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得分,数字小的人得分,然后各自弃置此轮所选的卡片弃置的卡片在此后轮次中不能使用则四轮比赛后,甲的总得分不小于的概率为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
设函数.
若,求函数的单调区间;
设函数在上有两个零点,求实数的取值范围其中是自然对数的底数
16.本小题分
记为数列的前项和,已知,.
求,并证明是等差数列;
求.
17.本小题分
如图,在四边形中,,,,.
求的大小;
求的面积的最大值;
若,求的面积.
18.本小题分
第十五届全国运动会将于年在广东、香港、澳门三地举办为了普及全运知识,某大学举办了一次全运知识闯关比赛,比赛分为初赛与复赛,初赛胜利后才能参加复赛,初赛规定:三人组队参赛,每次只派一个人,且每人只派一次;如果一个人闯关失败,再派下一个人重新闯关;三人中只要有人闯关成功即视作初赛胜利,无需继续闯关现有甲、乙、丙三人组队参加初赛,他们各自闯关成功的概率分别为、、,假定、、互不相等,且每人能否闯关成功相互独立.
若计划依次派甲、乙、丙进行初赛闯关,,求该小组初赛胜利的概率;
已知,若乙只能安排在第二个派出,要使初赛派出人员数目的期望较小,试确定甲、丙谁先派出;
初赛胜利小组的三名成员都可以进入复赛,复赛规定:单人参赛,每个人回答三道题,全部答对获得一等奖;答对两道题获得二等奖;答对一道题获得三等奖;全部答错不获奖,已知某学生进入了复赛,他在复赛中前两道题答对的概率均为,第三道题答对的概率为若他获得一等奖的概率为,设他获得二等奖的概率为,求的最小值.
19.本小题分
已知函数,其中是自然对数的底数.
当时,求在上的值域;
当时,讨论的零点个数;
当时,证明:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:当时,,的定义域为,
,
令,则,解得,
令,则,解得.
函数的单调递增区间为,单调递减区间为.
令,则.
令,其中,
则.
令,解得,令,解得.
的单调递减区间为,单调递增区间为,
.
又,函数在上有两个零点,
的取值范围是.
16.解:当时,,解得,
当时,,解得,
所以;
证明:由,得,则,
两式相减得,则,
令,则,,
所以是以为首项,以为公差的等差数列;
当为偶数时,
,
则.
17.解:在中,由正弦定理得,
因为,,所以,
因为,所以为锐角,可得,
所以;
在中,,
由余弦定理得,
整理得,当且仅当时取等号,
所以.
当时,的面积取得最大值;
因为,所以舍负.
可得.
在中,由正弦定理得,即,解得.
所以,即的面积为.
18.解:设事件表示该小组获胜,
则,
所以该小解组初赛胜利的概率为,
若依次派出甲乙丙进行闯关,设派出的人员数目为,
则的可能取值为,,,
则,
,
,
此时,
若依次派出丙乙甲进行闯关,设派出的人员数目为,
则的可能取值为,,,
则,
,
,
此时,
所以
,
因为,
所以,,
所以,
所以要使初赛派出人员数目的期望较小,先派出甲.
由题意可得,,
则,
令,
则,
令,
所以当时,,为减函数,
当时,,为增函数,
所以,
所以的最小值为.
19.解:当时,,,
,,
在上单调递减,
又,,
在上的值域为.
,
令得,
当时,,单调递减;
当时,,单调递增,
,
当时,,
,则在上有且仅有个零点;
当时,令,,
在上单调递增,
,即,又,
在上有个零点,又,
令,则,
在上单调递减,
,
,
在上有一个零点.
综上所述,时,有一个零点,
时,有个零点.
证明:当,时,,
设,
当时,,,
又由知,,
当时,,
设,则,
在单调递增,,
,即在单调递增,,
综上,,即当时,,
即.
第1页,共1页
同课章节目录
