湘教版数学九年级上册期中试卷(含答案)
文档属性
| 名称 | 湘教版数学九年级上册期中试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 216.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版数学九年级上册期中试卷
一、单选题
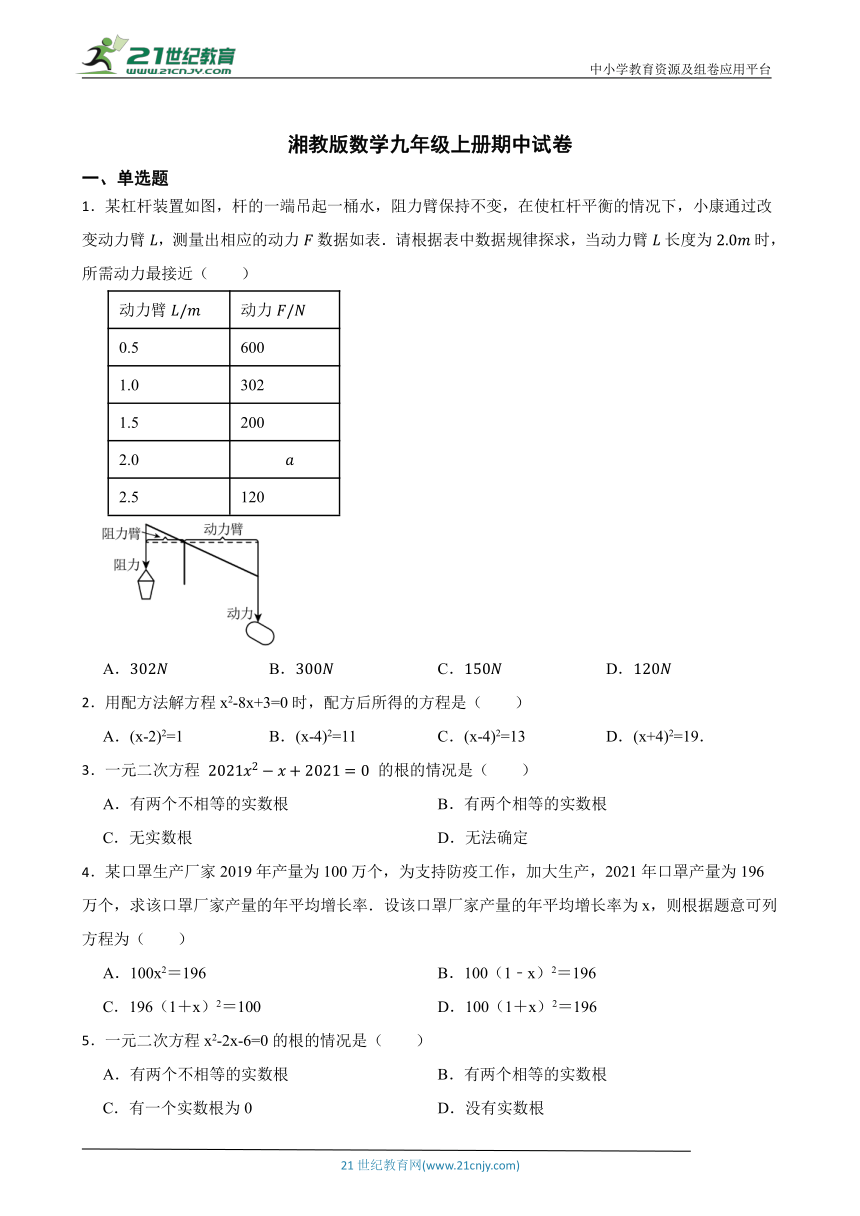
1.某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变,在使杠杆平衡的情况下,小康通过改变动力臂,测量出相应的动力数据如表.请根据表中数据规律探求,当动力臂长度为时,所需动力最接近( )
动力臂 动力
0.5 600
1.0 302
1.5 200
2.0
2.5 120
A. B. C. D.
2.用配方法解方程x2-8x+3=0时,配方后所得的方程是( )
A.(x-2)2=1 B.(x-4)2=11 C.(x-4)2=13 D.(x+4)2=19.
3.一元二次方程 的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
4.某口罩生产厂家2019年产量为100万个,为支持防疫工作,加大生产,2021年口罩产量为196万个,求该口罩厂家产量的年平均增长率.设该口罩厂家产量的年平均增长率为x,则根据题意可列方程为( )
A.100x2=196 B.100(1﹣x)2=196
C.196(1+x)2=100 D.100(1+x)2=196
5.一元二次方程x2-2x-6=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.有一个实数根为0 D.没有实数根
6.如图,直线a,b,c被直线,所截,交点分别为点A,C,E和点B,D,F.已知,且,,则的值是( )
A. B. C. D.
7.如图所示,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2设小路的宽为xcm,那么x满足的方程是( )
A.2x2-25x+16=0 B.x2-17x+16=0
C.x2-17x-16=0 D.x2-25x+32=0
8.香蕉是河口县的主要农副产品之一,香蕉的种植备受当地各农户的青睐.香蕉种植中,要注意病毒预防,香蕉有一种病叫“香蕉黄叶病”(又称“香蕉巴拿马病”),是一种通过土壤传播的香蕉传染病,染病香蕉逐步枯萎死亡,且因为土壤遗留,发病地区30年以上不能种植香蕉,是香蕉的“不治之症”.如果某农户家的一块香蕉地中有一棵香蕉感染了“巴拿马病毒”,经过两轮传染后有81棵香蕉被传染.请你用学过的知识分析,每轮传染中平均每棵香蕉传染的棵数为( ).
A.8棵 B.9棵 C.10棵 D.11棵
9.方程的解为( )
A. B.
C. D.
10.设a、b、c和S分别为三角形的三边长和面积,关于x的方程b2x2+(b2+c2-a2)x+c2=0的判别式为Δ.则Δ与S的大小关系为( ).
A.Δ=16S2 B.Δ=-16S2 C.Δ=16S D.Δ=-16S
二、填空题
11.方程 是关于x的一元二次方程,则m= .
12.反比例函数的图象上有三点,,,则,,的大小关系是 .
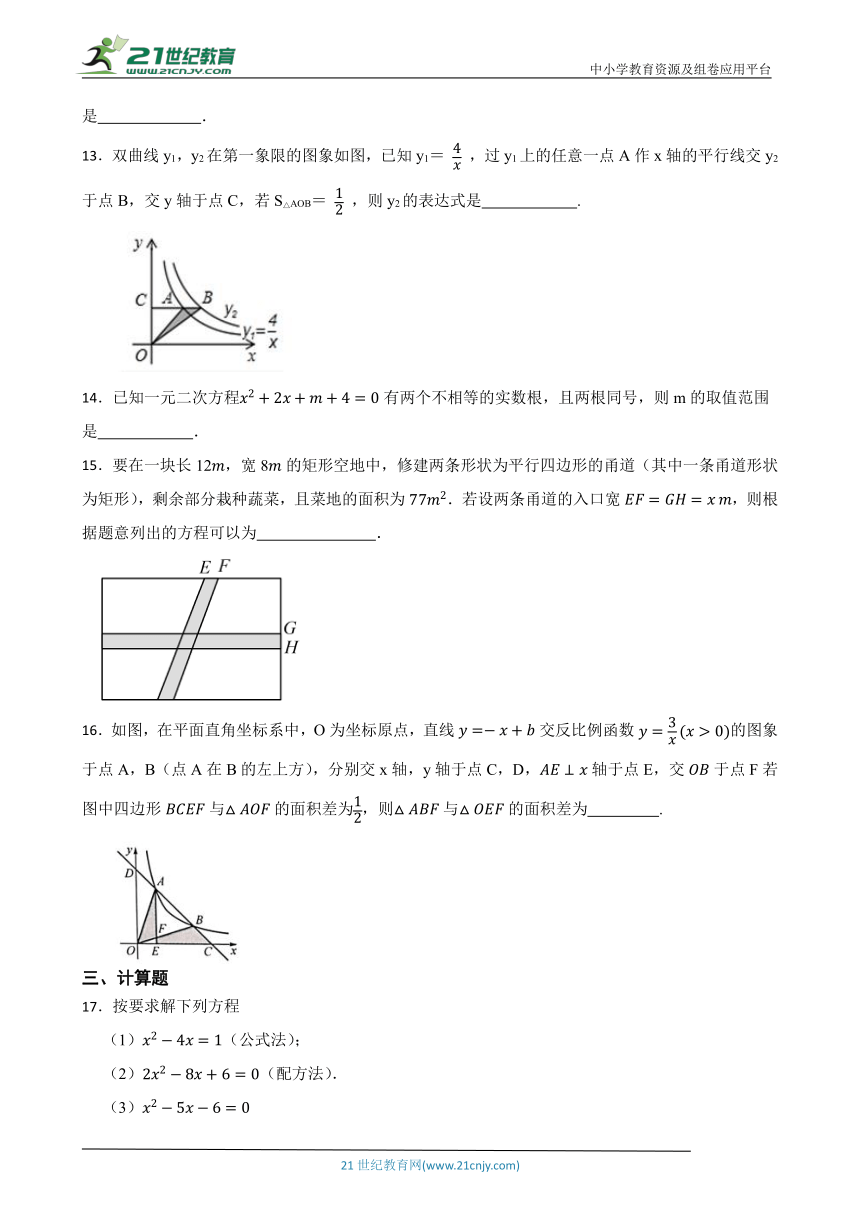
13.双曲线y1,y2在第一象限的图象如图,已知y1= ,过y1上的任意一点A作x轴的平行线交y2于点B,交y轴于点C,若S△AOB= ,则y2的表达式是 .
14.已知一元二次方程有两个不相等的实数根,且两根同号,则m的取值范围是 .
15.要在一块长12,宽8的矩形空地中,修建两条形状为平行四边形的甬道(其中一条甬道形状为矩形),剩余部分栽种蔬菜,且菜地的面积为.若设两条甬道的入口宽,则根据题意列出的方程可以为 .
16.如图,在平面直角坐标系中,O为坐标原点,直线交反比例函数的图象于点A,B(点A在B的左上方),分别交x轴,y轴于点C,D,轴于点E,交于点F若图中四边形与的面积差为,则与的面积差为 .
三、计算题
17.按要求解下列方程
(1)(公式法);
(2)(配方法).
(3)
(4)
18.解方程:(x-4)2=8-2x.
19.已知xyz≠0且 ,求k的值.
四、解答题
20.欣欣服装店经销某种品牌的童装,进价为元件,原来售价为元件,每天可以出售件,经市场调查发现每降价元,一天可以多售出件.
(1)如果每天的利润要比原来多元,并使顾客得到更大的优惠,问每件应降价多少元?
(2)由于库存原因,经理决定分两次降到以上价格,每次降价的百分率均为,求的值.
21.如图,已知一次函数的图像与反比例函数,分别交于点A 和点B,且A、B两点的坐标分别是和,连接、.
(1)求一次函数与反比例函数的函数表达式;
(2)求的面积.
22.某西瓜经营户以2元/千克的进价购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,该经营户要想每天赢利200元,应将每千克小型西瓜的售价降低多少元
23.公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售100个,6月份销售144个,且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为30元/个,测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元/个,则月销售量将减少10个,为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个?
答案解析部分
1.【答案】C
【知识点】反比例函数的实际应用
2.【答案】C
【知识点】配方法的应用
3.【答案】C
【知识点】一元二次方程根的判别式及应用
4.【答案】D
【知识点】一元二次方程的实际应用-百分率问题
5.【答案】A
【知识点】一元二次方程根的判别式及应用
6.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
7.【答案】B
【知识点】一元二次方程的应用-几何问题
8.【答案】A
【知识点】一元二次方程的实际应用-传染问题
9.【答案】D
【知识点】因式分解法解一元二次方程
10.【答案】B
【知识点】平方差公式及应用;一元二次方程根的判别式及应用
11.【答案】m=2
【知识点】一元二次方程的定义及相关的量
12.【答案】
【知识点】反比例函数的性质
13.【答案】y2=
【知识点】反比例函数系数k的几何意义
14.【答案】
【知识点】一元二次方程根的判别式及应用;一元二次方程的根与系数的关系(韦达定理);解一元一次不等式组
15.【答案】
【知识点】一元二次方程的应用-几何问题
16.【答案】2.5
【知识点】反比例函数系数k的几何意义;三角形的面积;反比例函数图象上点的坐标特征
17.【答案】(1)解:原方程变形得,
,
∴,,,
∴,
∴,
∴,;
(2)解:移项得,
,
二次项系数化为1得,
,
配方得,
,
即:,
两边开方得:
,
∴,;
(3)解:因式分解得,
,
∴,,
∴,;
(4)解:原方程变形得,
,
∴,;
【知识点】直接开平方法解一元二次方程;配方法解一元二次方程;公式法解一元二次方程;因式分解法解一元二次方程
18.【答案】解:(x-4)2+2(x-4)=0.
(x-4)(x-2)=0.
x-4=0或x-2=0.
x=4或x=2
【知识点】因式分解法解一元二次方程
19.【答案】解:∵xyz≠0,∴x、y、z均不为0,①当x+y+z≠0时,∵ ,∴k= =2,②当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,所以,k=-1,综上所述,k=2或-1.
【知识点】比例的性质
20.【答案】(1)降价19元
(2)10%
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
21.【答案】(1),
(2)
【知识点】反比例函数与一次函数的交点问题
22.【答案】解:每千克小型西瓜的售价降低x元,根据题意,得
(3-2-x)· -24=200,
整理,得 50x2-25x+3=0,
解得 : x1=0.2, x2=0.3.
答:应将每千克小型西瓜的售价降低0.2元或0.3元.
【知识点】一元二次方程的实际应用-销售问题
23.【答案】(1)设该品牌头盔销售量的月增长率为x,
由题意得,100(1+x)2=144,
解得x=20%或x=﹣2.2(舍去),
∴该品牌头盔销售量的月增长率为20%;
(2)设该品牌头盔的实际售价应定为m元,
由题意得(m﹣30)[600﹣10(m﹣40)]=10000,
整理得m2﹣130m+4000=0,
解得m=50或m=80,
∵尽可能让顾客得到实惠,
∴m=50,
∴该品牌头盔的实际售价应定为50元.
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
21世纪教育网(www.21cnjy.com)
湘教版数学九年级上册期中试卷
一、单选题
1.某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变,在使杠杆平衡的情况下,小康通过改变动力臂,测量出相应的动力数据如表.请根据表中数据规律探求,当动力臂长度为时,所需动力最接近( )
动力臂 动力
0.5 600
1.0 302
1.5 200
2.0
2.5 120
A. B. C. D.
2.用配方法解方程x2-8x+3=0时,配方后所得的方程是( )
A.(x-2)2=1 B.(x-4)2=11 C.(x-4)2=13 D.(x+4)2=19.
3.一元二次方程 的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.无法确定
4.某口罩生产厂家2019年产量为100万个,为支持防疫工作,加大生产,2021年口罩产量为196万个,求该口罩厂家产量的年平均增长率.设该口罩厂家产量的年平均增长率为x,则根据题意可列方程为( )
A.100x2=196 B.100(1﹣x)2=196
C.196(1+x)2=100 D.100(1+x)2=196
5.一元二次方程x2-2x-6=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.有一个实数根为0 D.没有实数根
6.如图,直线a,b,c被直线,所截,交点分别为点A,C,E和点B,D,F.已知,且,,则的值是( )
A. B. C. D.
7.如图所示,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2设小路的宽为xcm,那么x满足的方程是( )
A.2x2-25x+16=0 B.x2-17x+16=0
C.x2-17x-16=0 D.x2-25x+32=0
8.香蕉是河口县的主要农副产品之一,香蕉的种植备受当地各农户的青睐.香蕉种植中,要注意病毒预防,香蕉有一种病叫“香蕉黄叶病”(又称“香蕉巴拿马病”),是一种通过土壤传播的香蕉传染病,染病香蕉逐步枯萎死亡,且因为土壤遗留,发病地区30年以上不能种植香蕉,是香蕉的“不治之症”.如果某农户家的一块香蕉地中有一棵香蕉感染了“巴拿马病毒”,经过两轮传染后有81棵香蕉被传染.请你用学过的知识分析,每轮传染中平均每棵香蕉传染的棵数为( ).
A.8棵 B.9棵 C.10棵 D.11棵
9.方程的解为( )
A. B.
C. D.
10.设a、b、c和S分别为三角形的三边长和面积,关于x的方程b2x2+(b2+c2-a2)x+c2=0的判别式为Δ.则Δ与S的大小关系为( ).
A.Δ=16S2 B.Δ=-16S2 C.Δ=16S D.Δ=-16S
二、填空题
11.方程 是关于x的一元二次方程,则m= .
12.反比例函数的图象上有三点,,,则,,的大小关系是 .
13.双曲线y1,y2在第一象限的图象如图,已知y1= ,过y1上的任意一点A作x轴的平行线交y2于点B,交y轴于点C,若S△AOB= ,则y2的表达式是 .
14.已知一元二次方程有两个不相等的实数根,且两根同号,则m的取值范围是 .
15.要在一块长12,宽8的矩形空地中,修建两条形状为平行四边形的甬道(其中一条甬道形状为矩形),剩余部分栽种蔬菜,且菜地的面积为.若设两条甬道的入口宽,则根据题意列出的方程可以为 .
16.如图,在平面直角坐标系中,O为坐标原点,直线交反比例函数的图象于点A,B(点A在B的左上方),分别交x轴,y轴于点C,D,轴于点E,交于点F若图中四边形与的面积差为,则与的面积差为 .
三、计算题
17.按要求解下列方程
(1)(公式法);
(2)(配方法).
(3)
(4)
18.解方程:(x-4)2=8-2x.
19.已知xyz≠0且 ,求k的值.
四、解答题
20.欣欣服装店经销某种品牌的童装,进价为元件,原来售价为元件,每天可以出售件,经市场调查发现每降价元,一天可以多售出件.
(1)如果每天的利润要比原来多元,并使顾客得到更大的优惠,问每件应降价多少元?
(2)由于库存原因,经理决定分两次降到以上价格,每次降价的百分率均为,求的值.
21.如图,已知一次函数的图像与反比例函数,分别交于点A 和点B,且A、B两点的坐标分别是和,连接、.
(1)求一次函数与反比例函数的函数表达式;
(2)求的面积.
22.某西瓜经营户以2元/千克的进价购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,该经营户要想每天赢利200元,应将每千克小型西瓜的售价降低多少元
23.公安交警部门提醒市民,骑车出行必须严格遵守“一盔一带”的规定.某头盔经销商统计了某品牌头盔4月份到6月份的销量,该品牌头盔4月份销售100个,6月份销售144个,且从4月份到6月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为30元/个,测算在市场中,当售价为40元/个时,月销售量为600个,若在此基础上售价每上涨1元/个,则月销售量将减少10个,为使月销售利润达到10000元,而且尽可能让顾客得到实惠,则该品牌头盔的实际售价应定为多少元/个?
答案解析部分
1.【答案】C
【知识点】反比例函数的实际应用
2.【答案】C
【知识点】配方法的应用
3.【答案】C
【知识点】一元二次方程根的判别式及应用
4.【答案】D
【知识点】一元二次方程的实际应用-百分率问题
5.【答案】A
【知识点】一元二次方程根的判别式及应用
6.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
7.【答案】B
【知识点】一元二次方程的应用-几何问题
8.【答案】A
【知识点】一元二次方程的实际应用-传染问题
9.【答案】D
【知识点】因式分解法解一元二次方程
10.【答案】B
【知识点】平方差公式及应用;一元二次方程根的判别式及应用
11.【答案】m=2
【知识点】一元二次方程的定义及相关的量
12.【答案】
【知识点】反比例函数的性质
13.【答案】y2=
【知识点】反比例函数系数k的几何意义
14.【答案】
【知识点】一元二次方程根的判别式及应用;一元二次方程的根与系数的关系(韦达定理);解一元一次不等式组
15.【答案】
【知识点】一元二次方程的应用-几何问题
16.【答案】2.5
【知识点】反比例函数系数k的几何意义;三角形的面积;反比例函数图象上点的坐标特征
17.【答案】(1)解:原方程变形得,
,
∴,,,
∴,
∴,
∴,;
(2)解:移项得,
,
二次项系数化为1得,
,
配方得,
,
即:,
两边开方得:
,
∴,;
(3)解:因式分解得,
,
∴,,
∴,;
(4)解:原方程变形得,
,
∴,;
【知识点】直接开平方法解一元二次方程;配方法解一元二次方程;公式法解一元二次方程;因式分解法解一元二次方程
18.【答案】解:(x-4)2+2(x-4)=0.
(x-4)(x-2)=0.
x-4=0或x-2=0.
x=4或x=2
【知识点】因式分解法解一元二次方程
19.【答案】解:∵xyz≠0,∴x、y、z均不为0,①当x+y+z≠0时,∵ ,∴k= =2,②当x+y+z=0时,x+y=-z,z+x=-y,y+z=-x,所以,k=-1,综上所述,k=2或-1.
【知识点】比例的性质
20.【答案】(1)降价19元
(2)10%
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
21.【答案】(1),
(2)
【知识点】反比例函数与一次函数的交点问题
22.【答案】解:每千克小型西瓜的售价降低x元,根据题意,得
(3-2-x)· -24=200,
整理,得 50x2-25x+3=0,
解得 : x1=0.2, x2=0.3.
答:应将每千克小型西瓜的售价降低0.2元或0.3元.
【知识点】一元二次方程的实际应用-销售问题
23.【答案】(1)设该品牌头盔销售量的月增长率为x,
由题意得,100(1+x)2=144,
解得x=20%或x=﹣2.2(舍去),
∴该品牌头盔销售量的月增长率为20%;
(2)设该品牌头盔的实际售价应定为m元,
由题意得(m﹣30)[600﹣10(m﹣40)]=10000,
整理得m2﹣130m+4000=0,
解得m=50或m=80,
∵尽可能让顾客得到实惠,
∴m=50,
∴该品牌头盔的实际售价应定为50元.
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
21世纪教育网(www.21cnjy.com)
同课章节目录
