人教版五年级上册第六单元平行四边行的面积教案
文档属性
| 名称 | 人教版五年级上册第六单元平行四边行的面积教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 15:18:47 | ||
图片预览


文档简介
《平行四边形的面积》教案
教学目标:
1、知识与能力目标:通过学生自主探索、动手实践推导出平行四边形面积计算公式,理解和掌握平行四边形的面积计算公式,能正确求平行四边形的面积。
2、过程与方法目标:让学生经历平行四边形面积公式的推导过程,通过操作、观察、比较活动,初步认识转化的方法,发展学生的空间观念。
3、情感态度与价值观目标:培养学生的分析、综合、抽象、概括和解决实际问题的能力;使学生感受数学与生活的联系,培养学生的数学应用意识,体验数学的价值。
教学重点、难点
教学重点:探究并推导平行四边形面积的计算公式,并能正确运用。
教学难点:通过学生动手操作,用割补的方法把一个平行四边形转化为一个长方形,找出两个图形之间的联系,推导出平行四边形面积的计算公式。
关键点:通过引导学生提出假设——动手操作——推导——概括的步骤开展探究活动,利用知识迁移及剪、移、拼的实际操作来分解教学难点即平行四边形面积公式的推导。关键是通过“剪、移、拼”将平行四边形转化成长方形后,找出平行四边形底和高与长方形长和宽的关系,及面积不变的特点,从而理解平行四边形面积的推导过程。
教具、学具准备:
多媒体课件、平行四边形纸片、剪刀、三角板等。
教学过程:
一、创设情境,导入新课
1、师:同学们看这幅图,找一找图中有哪些学过的图形。
2、师:这个花坛什么形状?以前我们学习了长方形的面积,(出示:小精灵的声音:同学们,知道怎样求长方形的面积吗?在最初的时候,人们只会用最原始的方法拿一个个面积单位去铺去摆,如果面积单位是1cm2,一共铺了12个,面积就是12 cm2,这种直接铺直接数的方法,叫直接测量。)(动画演示)
师:你们觉得这种方法怎么样?(比较麻烦)人们经过实践找到另一种求长方形面积的方法,还记得这个公式吗?
生:长方形面积=长×宽。(板书:长方形面积=长×宽)(出示:小精灵声音:这个长方形长4厘米,宽3厘米,长方形面积=长×宽,4×3=12 cm2。)
师:有了这个成果,人们也会以此类推求出其他平面图形的面积,比如说,
这个花坛,它是什么形状?(平行四边形)它的面积怎么求呢?这节课我们就来研究平行四边形的面积。(板书:平行四边形的面积)
二、动手操作,探究新知
1、猜一猜:
师:先来猜猜它的面积可能怎么求?
生:边×边。
师:哦,他的意思是用一条边×另一条边,也就是边×邻边(板书)。我们把这个想法叫做××猜想。同意这个猜想的同学举手。如果要求它的面积,你想知道哪些数据?好,老师给你这两个数据:一条边长6m,一条边长5m。请你计算它的面积。哦,6×5=30 m2。
师:还有别的猜想吗?
生:底×高(指一指底和高在哪里)
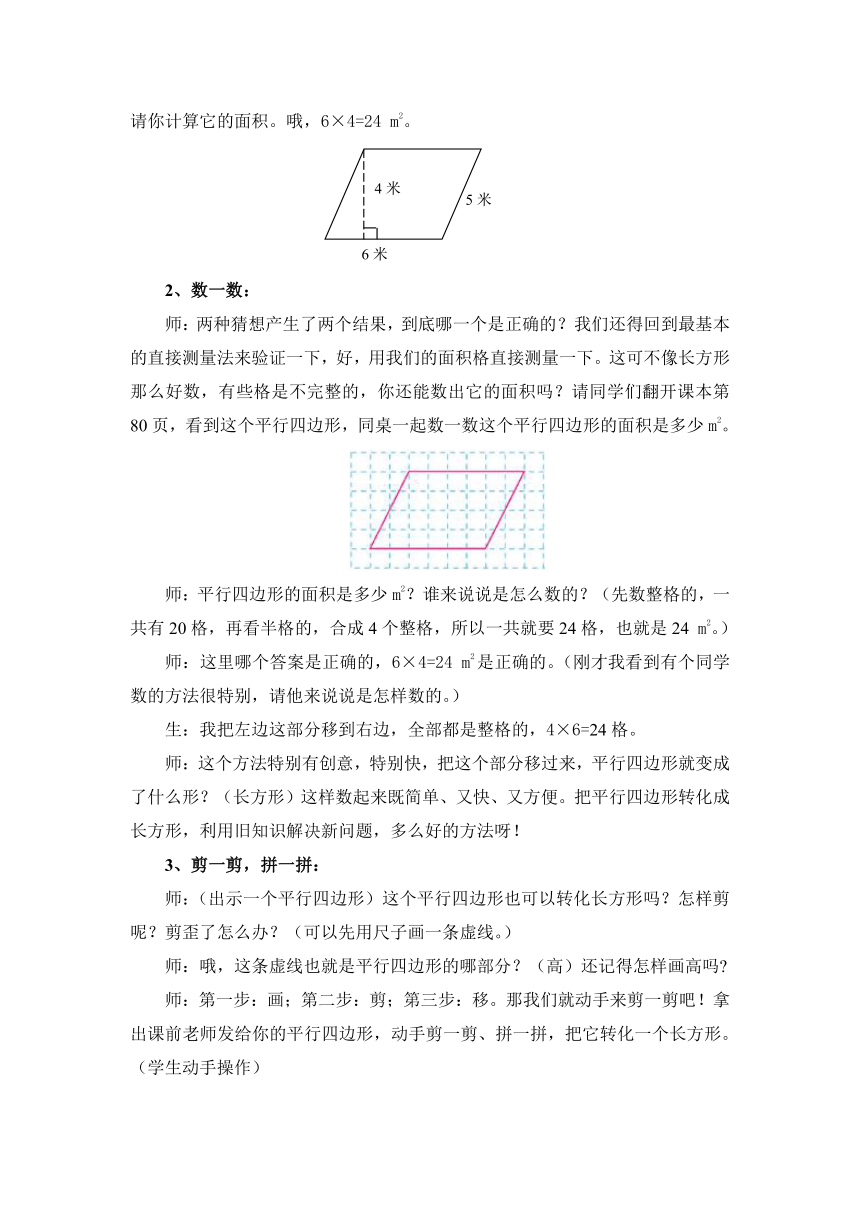
师:我们把这个猜想叫××猜想。(板书)同意这个猜想的同学举手。如果要求它的面积,你想量出哪些数据?好,老师也给你两个数据:底6 m,高4m,请你计算它的面积。哦,6×4=24 m2。
2、数一数:
师:两种猜想产生了两个结果,到底哪一个是正确的?我们还得回到最基本的直接测量法来验证一下,好,用我们的面积格直接测量一下。这可不像长方形那么好数,有些格是不完整的,你还能数出它的面积吗?请同学们翻开课本第80页,看到这个平行四边形,同桌一起数一数这个平行四边形的面积是多少m2。
师:平行四边形的面积是多少m2?谁来说说是怎么数的?(先数整格的,一共有20格,再看半格的,合成4个整格,所以一共就要24格,也就是24 m2。)
师:这里哪个答案是正确的,6×4=24 m2是正确的。(刚才我看到有个同学数的方法很特别,请他来说说是怎样数的。)
生:我把左边这部分移到右边,全部都是整格的,4×6=24格。
师:这个方法特别有创意,特别快,把这个部分移过来,平行四边形就变成了什么形?(长方形)这样数起来既简单、又快、又方便。把平行四边形转化成长方形,利用旧知识解决新问题,多么好的方法呀!
3、剪一剪,拼一拼:
师:(出示一个平行四边形)这个平行四边形也可以转化长方形吗?怎样剪呢?剪歪了怎么办?(可以先用尺子画一条虚线。)
师:哦,这条虚线也就是平行四边形的哪部分?(高)还记得怎样画高吗
师:第一步:画;第二步:剪;第三步:移。那我们就动手来剪一剪吧!拿出课前老师发给你的平行四边形,动手剪一剪、拼一拼,把它转化一个长方形。(学生动手操作)
师:拼成长方形了吗?拼好了摆在桌面给老师看看,请两个同学来前面展示他们的作品,(指名上黑板前)说说你是怎样操作的?(我先画条高,沿着高剪开,把这部分移过去,就拼成了一个长方形。)
师:怎样移过去呀?哦,平着移到右边,这种方法我们把它叫做平移。
师:再请一个同学展示一下,他的剪法有什么不一样吗?(在中间剪的)剪成两个梯形,可以吗?平移过去也拼成了一个长方形。(贴在黑板上)
师:看看操作。(展示)
4、议一议:
师:老师有几个问题,我们把平行四边形转化成了了长方形,原来平行四边形的面积和这个长方形的面积相等吗?平行四边形的底和高分别与长方形的长和宽有什么关系呢?
小组讨论:
⑴ 原来平行四边形的面积和拼成的长方形的面积相等吗?
⑵ 原来平行四边形的底与拼成的长方形的长有什么关系?
⑶ 原来平行四边形的高与拼成的长方形的宽有什么关系?
师:谁来说说你的想法。它的面积没有多,也没有少,平行四边形的面积等于剪拼后的长方形的面积。(板书)平行四边形的底和高与长方形的长和宽有什么关系?我们看演示。(板书:底=长 宽=高)
师:长方形的面积=长×宽,那么平行四边形的面积怎样求?
生:平行四边形的面积=底×高(板书)
师:同意吗?同学们想的和数学家想的一模一样。谁能讲一讲,为什么平行四边形的面积=底×高?结合刚才一剪一拼的过程说说。(生说。)
师:沿着平行四边形的高剪成两部分,平移过去拼成了长方形。平行四边形的面积等于拼成的长方形的面积,平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽,长方形的的面积=长×高,所以,平行四边形的面积=底×高。你也能这么严谨地说一遍吗?同桌两个试着说一遍。(指名说一说)
师:如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形的面积计算公式可以写成S=ah(板书S=ah)。
师:现在我们可以确定当初的猜想谁是正确的?
师:这样猜的同学别气馁,你们知道吗?有资料显示在几千年前的古埃及的数学家可能就是这么猜的。你们敢猜,已经很棒了。
三、分层训练,巩固内化
㈠ 基本练习:
1、例1:平行四边形花坛的底是6厘米m,高是4m,它的面积是多少?
㈡ 综合练习:
1、只列式不计算:(3道)
师:只列式,不计算。
2、判断:
(1) 平行四边形的面积等于长方形的面积。 ( )
(2) 平行四边形的面积=底×高。 ( )
(3) 一块平行四边形菜地的底是9米,高是5米,它的面积是45米。( )
(4) 一个平行四边形的面积是10平方厘米,它的底是5厘米,高是2厘米。( )
3、你能想办法求出下面平行四边形的面积吗?先说说你会怎样做?(先画出一条高,量出高和底的长度,再用底×高就求出平行四边形的面积)
㈢ 扩展练习:
1.下面图中平行四边形的面积相等吗?你想到了什么?
2、下图中正方形的周长是32㎝。
四、总结:
师:这节课你有什么有收获?
师:同学们学得非常认真,我们通过把平行四边形转化成长方形推导出了平行四边形的面积,这种方法很好,变新知识为旧知识,在以后的学习中我们会常用到这种方法,希望同学在以后的学习中也多动脑筋。
6米
5米
4米
25 m
20 m
12cm
8cm
9.6 m
18 m
26 m
教学目标:
1、知识与能力目标:通过学生自主探索、动手实践推导出平行四边形面积计算公式,理解和掌握平行四边形的面积计算公式,能正确求平行四边形的面积。
2、过程与方法目标:让学生经历平行四边形面积公式的推导过程,通过操作、观察、比较活动,初步认识转化的方法,发展学生的空间观念。
3、情感态度与价值观目标:培养学生的分析、综合、抽象、概括和解决实际问题的能力;使学生感受数学与生活的联系,培养学生的数学应用意识,体验数学的价值。
教学重点、难点
教学重点:探究并推导平行四边形面积的计算公式,并能正确运用。
教学难点:通过学生动手操作,用割补的方法把一个平行四边形转化为一个长方形,找出两个图形之间的联系,推导出平行四边形面积的计算公式。
关键点:通过引导学生提出假设——动手操作——推导——概括的步骤开展探究活动,利用知识迁移及剪、移、拼的实际操作来分解教学难点即平行四边形面积公式的推导。关键是通过“剪、移、拼”将平行四边形转化成长方形后,找出平行四边形底和高与长方形长和宽的关系,及面积不变的特点,从而理解平行四边形面积的推导过程。
教具、学具准备:
多媒体课件、平行四边形纸片、剪刀、三角板等。
教学过程:
一、创设情境,导入新课
1、师:同学们看这幅图,找一找图中有哪些学过的图形。
2、师:这个花坛什么形状?以前我们学习了长方形的面积,(出示:小精灵的声音:同学们,知道怎样求长方形的面积吗?在最初的时候,人们只会用最原始的方法拿一个个面积单位去铺去摆,如果面积单位是1cm2,一共铺了12个,面积就是12 cm2,这种直接铺直接数的方法,叫直接测量。)(动画演示)
师:你们觉得这种方法怎么样?(比较麻烦)人们经过实践找到另一种求长方形面积的方法,还记得这个公式吗?
生:长方形面积=长×宽。(板书:长方形面积=长×宽)(出示:小精灵声音:这个长方形长4厘米,宽3厘米,长方形面积=长×宽,4×3=12 cm2。)
师:有了这个成果,人们也会以此类推求出其他平面图形的面积,比如说,
这个花坛,它是什么形状?(平行四边形)它的面积怎么求呢?这节课我们就来研究平行四边形的面积。(板书:平行四边形的面积)
二、动手操作,探究新知
1、猜一猜:
师:先来猜猜它的面积可能怎么求?
生:边×边。
师:哦,他的意思是用一条边×另一条边,也就是边×邻边(板书)。我们把这个想法叫做××猜想。同意这个猜想的同学举手。如果要求它的面积,你想知道哪些数据?好,老师给你这两个数据:一条边长6m,一条边长5m。请你计算它的面积。哦,6×5=30 m2。
师:还有别的猜想吗?
生:底×高(指一指底和高在哪里)
师:我们把这个猜想叫××猜想。(板书)同意这个猜想的同学举手。如果要求它的面积,你想量出哪些数据?好,老师也给你两个数据:底6 m,高4m,请你计算它的面积。哦,6×4=24 m2。
2、数一数:
师:两种猜想产生了两个结果,到底哪一个是正确的?我们还得回到最基本的直接测量法来验证一下,好,用我们的面积格直接测量一下。这可不像长方形那么好数,有些格是不完整的,你还能数出它的面积吗?请同学们翻开课本第80页,看到这个平行四边形,同桌一起数一数这个平行四边形的面积是多少m2。
师:平行四边形的面积是多少m2?谁来说说是怎么数的?(先数整格的,一共有20格,再看半格的,合成4个整格,所以一共就要24格,也就是24 m2。)
师:这里哪个答案是正确的,6×4=24 m2是正确的。(刚才我看到有个同学数的方法很特别,请他来说说是怎样数的。)
生:我把左边这部分移到右边,全部都是整格的,4×6=24格。
师:这个方法特别有创意,特别快,把这个部分移过来,平行四边形就变成了什么形?(长方形)这样数起来既简单、又快、又方便。把平行四边形转化成长方形,利用旧知识解决新问题,多么好的方法呀!
3、剪一剪,拼一拼:
师:(出示一个平行四边形)这个平行四边形也可以转化长方形吗?怎样剪呢?剪歪了怎么办?(可以先用尺子画一条虚线。)
师:哦,这条虚线也就是平行四边形的哪部分?(高)还记得怎样画高吗
师:第一步:画;第二步:剪;第三步:移。那我们就动手来剪一剪吧!拿出课前老师发给你的平行四边形,动手剪一剪、拼一拼,把它转化一个长方形。(学生动手操作)
师:拼成长方形了吗?拼好了摆在桌面给老师看看,请两个同学来前面展示他们的作品,(指名上黑板前)说说你是怎样操作的?(我先画条高,沿着高剪开,把这部分移过去,就拼成了一个长方形。)
师:怎样移过去呀?哦,平着移到右边,这种方法我们把它叫做平移。
师:再请一个同学展示一下,他的剪法有什么不一样吗?(在中间剪的)剪成两个梯形,可以吗?平移过去也拼成了一个长方形。(贴在黑板上)
师:看看操作。(展示)
4、议一议:
师:老师有几个问题,我们把平行四边形转化成了了长方形,原来平行四边形的面积和这个长方形的面积相等吗?平行四边形的底和高分别与长方形的长和宽有什么关系呢?
小组讨论:
⑴ 原来平行四边形的面积和拼成的长方形的面积相等吗?
⑵ 原来平行四边形的底与拼成的长方形的长有什么关系?
⑶ 原来平行四边形的高与拼成的长方形的宽有什么关系?
师:谁来说说你的想法。它的面积没有多,也没有少,平行四边形的面积等于剪拼后的长方形的面积。(板书)平行四边形的底和高与长方形的长和宽有什么关系?我们看演示。(板书:底=长 宽=高)
师:长方形的面积=长×宽,那么平行四边形的面积怎样求?
生:平行四边形的面积=底×高(板书)
师:同意吗?同学们想的和数学家想的一模一样。谁能讲一讲,为什么平行四边形的面积=底×高?结合刚才一剪一拼的过程说说。(生说。)
师:沿着平行四边形的高剪成两部分,平移过去拼成了长方形。平行四边形的面积等于拼成的长方形的面积,平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽,长方形的的面积=长×高,所以,平行四边形的面积=底×高。你也能这么严谨地说一遍吗?同桌两个试着说一遍。(指名说一说)
师:如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形的面积计算公式可以写成S=ah(板书S=ah)。
师:现在我们可以确定当初的猜想谁是正确的?
师:这样猜的同学别气馁,你们知道吗?有资料显示在几千年前的古埃及的数学家可能就是这么猜的。你们敢猜,已经很棒了。
三、分层训练,巩固内化
㈠ 基本练习:
1、例1:平行四边形花坛的底是6厘米m,高是4m,它的面积是多少?
㈡ 综合练习:
1、只列式不计算:(3道)
师:只列式,不计算。
2、判断:
(1) 平行四边形的面积等于长方形的面积。 ( )
(2) 平行四边形的面积=底×高。 ( )
(3) 一块平行四边形菜地的底是9米,高是5米,它的面积是45米。( )
(4) 一个平行四边形的面积是10平方厘米,它的底是5厘米,高是2厘米。( )
3、你能想办法求出下面平行四边形的面积吗?先说说你会怎样做?(先画出一条高,量出高和底的长度,再用底×高就求出平行四边形的面积)
㈢ 扩展练习:
1.下面图中平行四边形的面积相等吗?你想到了什么?
2、下图中正方形的周长是32㎝。
四、总结:
师:这节课你有什么有收获?
师:同学们学得非常认真,我们通过把平行四边形转化成长方形推导出了平行四边形的面积,这种方法很好,变新知识为旧知识,在以后的学习中我们会常用到这种方法,希望同学在以后的学习中也多动脑筋。
6米
5米
4米
25 m
20 m
12cm
8cm
9.6 m
18 m
26 m
