相似三角形的性质(第2课时 ) 相似三角形的周长和面积之比课件(25张PPT)2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 相似三角形的性质(第2课时 ) 相似三角形的周长和面积之比课件(25张PPT)2024-2025学年北师大版九年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 21:10:47 | ||
图片预览




文档简介
(共25张PPT)
第四章 图形的相似
4.7 相似三角形的性质
第2课时 相似三角形的周长和面积之比
九年级上册数学(北师版)
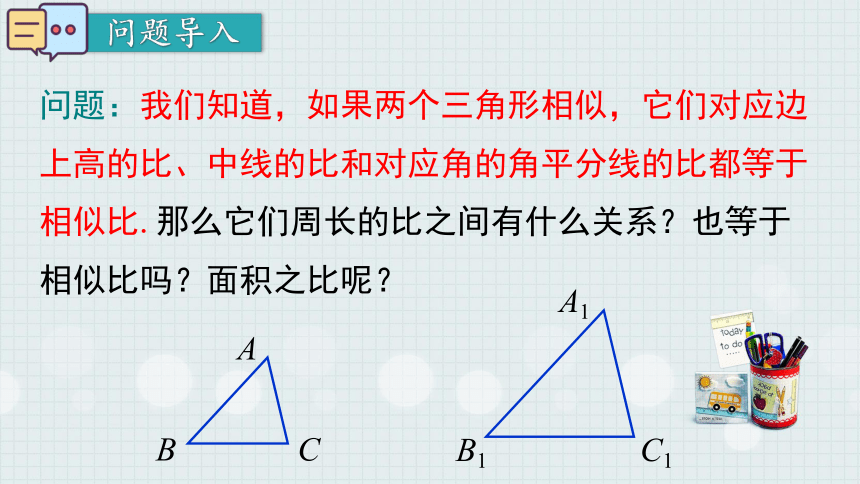
问题:我们知道,如果两个三角形相似,它们对应边上高的比、中线的比和对应角的角平分线的比都等于相似比.那么它们周长的比之间有什么关系?也等于相似比吗?面积之比呢?
A
B
C
A1
B1
C1
问题导入
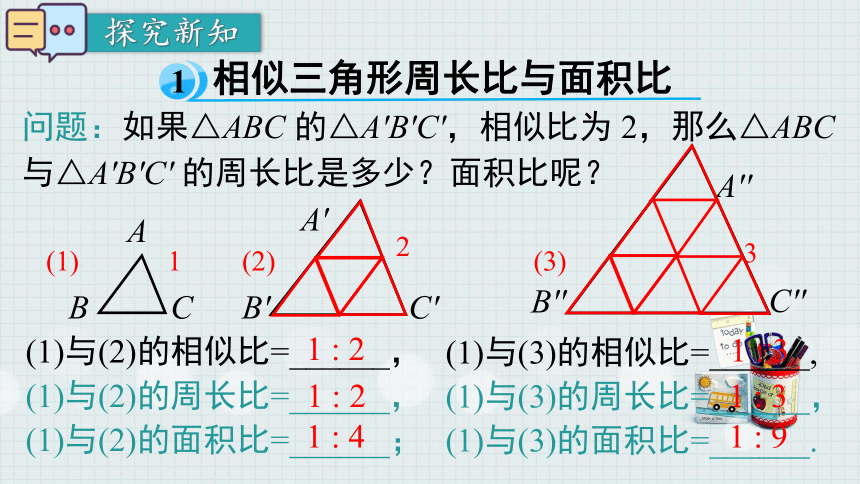
问题:如果△ABC 的△A'B'C',相似比为 2,那么△ABC 与△A'B'C' 的周长比是多少?面积比呢?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(2)的面积比=______;
1 : 2
1 : 2
1 : 3
1 : 3
探究新知
相似三角形周长比与面积比
1
(1)与(3)的相似比=______,
(1)与(3)的周长比=______,
(1)与(3)的面积比=______.
A
B
C
A'
B'
C'
A''
B''
C''
1 : 4
1 : 9
如果 △ABC 的 △A'B'C',相似比为 k,那么你能求 △ABC 与△A'B'C' 的周长比和面积比吗?
猜一猜
猜想1:相似三角形的周长比等于 .
相似比
猜想2:相似三角形的面积比等于 .
相似比的平方
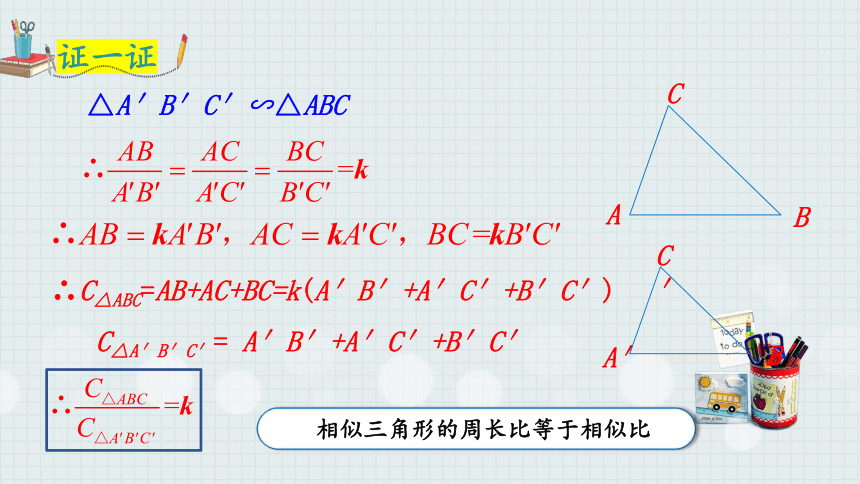
△A′B′C′∽△ABC
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′)
C△A′B′C′= A′B′+A′C′+B′C′
相似三角形的周长比等于相似比
A
B
C
A′
B′
C′
证一证
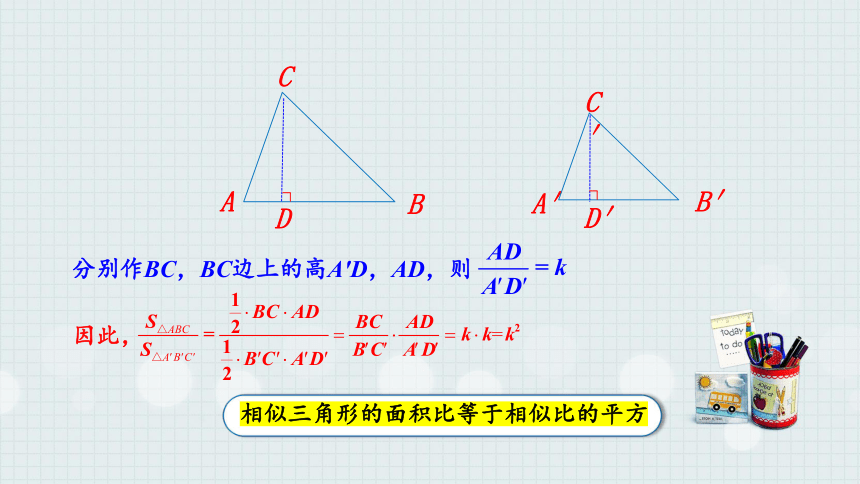
分别作BC,BC边上的高A′D,AD,则
因此,
相似三角形的面积比等于相似比的平方
A
B
C
A′
B′
C′
D
D′
相似三角形的面积比等于相似比的平方.
归纳总结
相似三角形周长的比等于相似比.
1. 已知 △ABC 与 △A′B′C′ 的相似比为 2 : 3,则对应边上中线之比 ,面积之比为 .
2. 如果两个相似三角形的面积之比为 1 : 9,
周长的比为______ .
1 : 3
2 : 3
4 : 9
练一练
议一议
两个相似四边形的周长等于相似比吗?面积比等于相似比的平方吗?两个相似五边形的周长比及面积比怎样呢?两个相似的n边形呢?
A
B
C
D
A′
B′
C′
D′
A
B
C
D
A′
B′
C′
D′
连接BD和B′D′
∵四边形ABCD∽四边形A′B′C′D′
A
B
C
D
A′
B′
C′
D′
连接BD和B′D′
相似多边形周长的比等于相似比,
面积比等于相似比的平方。
A
B
C
D
A′
B′
C′
D′
A
B
C
D
E
A′
B′
C′
D′
E′
(3) = , = .
(4) 四边形 A1B1C1D1 与四边形 A2B2C2D2 的面积比是多少?
A1
B1
C1
D1
A2
B2
C2
D2
两个相似五边形的周长比及面积比怎样呢?两个相似的 n 边形呢?
周长的比等于相似比,
面积比等于相似比的平方.
k2
k2
例1 如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC(两角分别相等的两个三角形相似).
(相似三角形的面积比等于相似的平方比)
即
∴EC2=2.∴EC= .∴BE=BC-EC= ,
即△ACB平移的距离为 .
例2 如图,D,E 分别是 AC,AB 上的点,已知 △ABC 的面积为 100 cm2,且 ,求四边形 BCDE 的面积.
B
C
A
D
E
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,∴ 面积比为 9 : 25.
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为 100-36 = 64 (cm2).
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC .
∵相似比为 1 : 2,∴面积比为 1 : 4.
∴
练一练
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,
面积比为 1 : 4.
设 S△ABC = 4,则 S△ADE = 1,S△EFC = 1.
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2.
∴ S四边形BFED : S△ABC = 2 : 4 =
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个
三角形的周长也扩大为原来的 5 倍 ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个
四边形的面积也扩大为原来的 9 倍 ( )
√
×
课堂练习
3. 连接三角形两边中点的线段把三角形截成的一个
小三角形与原三角形的周长比等于______,面积
比等于_____.
1 : 2
1 : 4
2. 在 △ABC 和 △DEF 中,AB=2DE,AC=2DF,
∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ
的值为 ( )
A.2 B.4 C.1 D.
C
4. △ABC 中,DE∥BC,EF∥AB,已知 △ADE 和 △EFC 的面积分别为 4 和 9,求 △ABC 的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF.
∴△ADE ∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC = 2 : 3,则 AE : AC = 2 : 5.
∴ S△ADE : S△ABC = 4 : 25. ∴ S△ABC = 25.
2.如图,△ABC中,DE∥FG∥BC,且DE、FG把△ABC的面积三等分,若BC=12cm,求FG的长.
又因为FG∥BC,所以 ,且
BC=12cm,所以FG = cm.
解:因为DE∥FG∥BC,
所以△ADE∽△AFG∽△ABC,
所以S△ADE∶S△AFG∶S△ABC=AD2∶AF2∶AB2,
又因为DE、FG把△ABC的面积三等分,
所以S△ADE∶S△AFG∶S△ABC=1∶2∶3,
所以AD∶AF∶AB= ,
3.如图,已知DE∥BC,BD=3AD,S△ABC =48,求:△ADE的面积.
解:因为DE∥BC
所以∠ADE=∠ABC, ∠AED=∠ACB
所以△ADE ∽△ABC
又因为BD=3AD
可得相似比k=AD∶AB=1∶2
所以S△ADE = S△ABC =12
课堂小结
相似三角形的周长的比等于相似比,面积比等于相似比的平方.
相似多边形的周长的比等于相似比,面积比等于相似比的平方.
相似三角形的性质(2)
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
当堂小结
第四章 图形的相似
4.7 相似三角形的性质
第2课时 相似三角形的周长和面积之比
九年级上册数学(北师版)
问题:我们知道,如果两个三角形相似,它们对应边上高的比、中线的比和对应角的角平分线的比都等于相似比.那么它们周长的比之间有什么关系?也等于相似比吗?面积之比呢?
A
B
C
A1
B1
C1
问题导入
问题:如果△ABC 的△A'B'C',相似比为 2,那么△ABC 与△A'B'C' 的周长比是多少?面积比呢?
(1)
(2)
(3)
1
2
3
(1)与(2)的相似比=______,
(1)与(2)的周长比=______,
(1)与(2)的面积比=______;
1 : 2
1 : 2
1 : 3
1 : 3
探究新知
相似三角形周长比与面积比
1
(1)与(3)的相似比=______,
(1)与(3)的周长比=______,
(1)与(3)的面积比=______.
A
B
C
A'
B'
C'
A''
B''
C''
1 : 4
1 : 9
如果 △ABC 的 △A'B'C',相似比为 k,那么你能求 △ABC 与△A'B'C' 的周长比和面积比吗?
猜一猜
猜想1:相似三角形的周长比等于 .
相似比
猜想2:相似三角形的面积比等于 .
相似比的平方
△A′B′C′∽△ABC
∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′)
C△A′B′C′= A′B′+A′C′+B′C′
相似三角形的周长比等于相似比
A
B
C
A′
B′
C′
证一证
分别作BC,BC边上的高A′D,AD,则
因此,
相似三角形的面积比等于相似比的平方
A
B
C
A′
B′
C′
D
D′
相似三角形的面积比等于相似比的平方.
归纳总结
相似三角形周长的比等于相似比.
1. 已知 △ABC 与 △A′B′C′ 的相似比为 2 : 3,则对应边上中线之比 ,面积之比为 .
2. 如果两个相似三角形的面积之比为 1 : 9,
周长的比为______ .
1 : 3
2 : 3
4 : 9
练一练
议一议
两个相似四边形的周长等于相似比吗?面积比等于相似比的平方吗?两个相似五边形的周长比及面积比怎样呢?两个相似的n边形呢?
A
B
C
D
A′
B′
C′
D′
A
B
C
D
A′
B′
C′
D′
连接BD和B′D′
∵四边形ABCD∽四边形A′B′C′D′
A
B
C
D
A′
B′
C′
D′
连接BD和B′D′
相似多边形周长的比等于相似比,
面积比等于相似比的平方。
A
B
C
D
A′
B′
C′
D′
A
B
C
D
E
A′
B′
C′
D′
E′
(3) = , = .
(4) 四边形 A1B1C1D1 与四边形 A2B2C2D2 的面积比是多少?
A1
B1
C1
D1
A2
B2
C2
D2
两个相似五边形的周长比及面积比怎样呢?两个相似的 n 边形呢?
周长的比等于相似比,
面积比等于相似比的平方.
k2
k2
例1 如图,将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC(两角分别相等的两个三角形相似).
(相似三角形的面积比等于相似的平方比)
即
∴EC2=2.∴EC= .∴BE=BC-EC= ,
即△ACB平移的距离为 .
例2 如图,D,E 分别是 AC,AB 上的点,已知 △ABC 的面积为 100 cm2,且 ,求四边形 BCDE 的面积.
B
C
A
D
E
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,∴ 面积比为 9 : 25.
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为 100-36 = 64 (cm2).
如图,△ABC 中,点 D、E、F 分别在 AB、AC、BC 上,且 DE∥BC,EF∥AB. 当 D 点为 AB 中点时,求 S四边形BFED : S△ABC 的值.
A
B
C
D
F
E
解:∵ DE∥BC,D 为 AB 中点,
∴ △ADE ∽ △ABC .
∵相似比为 1 : 2,∴面积比为 1 : 4.
∴
练一练
A
B
C
D
F
E
又∵ EF∥AB,
∴ △EFC ∽ △ABC ,相似比为 1 : 2,
面积比为 1 : 4.
设 S△ABC = 4,则 S△ADE = 1,S△EFC = 1.
S四边形BFED = S△ABC-S△ADE-S△EFC = 4-1-1 = 2.
∴ S四边形BFED : S△ABC = 2 : 4 =
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个
三角形的周长也扩大为原来的 5 倍 ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个
四边形的面积也扩大为原来的 9 倍 ( )
√
×
课堂练习
3. 连接三角形两边中点的线段把三角形截成的一个
小三角形与原三角形的周长比等于______,面积
比等于_____.
1 : 2
1 : 4
2. 在 △ABC 和 △DEF 中,AB=2DE,AC=2DF,
∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ
的值为 ( )
A.2 B.4 C.1 D.
C
4. △ABC 中,DE∥BC,EF∥AB,已知 △ADE 和 △EFC 的面积分别为 4 和 9,求 △ABC 的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ △ADE ∽△ABC,∠ADE =∠EFC,∠A =∠CEF.
∴△ADE ∽△EFC.
又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC = 2 : 3,则 AE : AC = 2 : 5.
∴ S△ADE : S△ABC = 4 : 25. ∴ S△ABC = 25.
2.如图,△ABC中,DE∥FG∥BC,且DE、FG把△ABC的面积三等分,若BC=12cm,求FG的长.
又因为FG∥BC,所以 ,且
BC=12cm,所以FG = cm.
解:因为DE∥FG∥BC,
所以△ADE∽△AFG∽△ABC,
所以S△ADE∶S△AFG∶S△ABC=AD2∶AF2∶AB2,
又因为DE、FG把△ABC的面积三等分,
所以S△ADE∶S△AFG∶S△ABC=1∶2∶3,
所以AD∶AF∶AB= ,
3.如图,已知DE∥BC,BD=3AD,S△ABC =48,求:△ADE的面积.
解:因为DE∥BC
所以∠ADE=∠ABC, ∠AED=∠ACB
所以△ADE ∽△ABC
又因为BD=3AD
可得相似比k=AD∶AB=1∶2
所以S△ADE = S△ABC =12
课堂小结
相似三角形的周长的比等于相似比,面积比等于相似比的平方.
相似多边形的周长的比等于相似比,面积比等于相似比的平方.
相似三角形的性质(2)
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
当堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
