2024—2025年山东省济南市历程第一中学高二第一学期九月份数学月考试题(含答案)
文档属性
| 名称 | 2024—2025年山东省济南市历程第一中学高二第一学期九月份数学月考试题(含答案) | 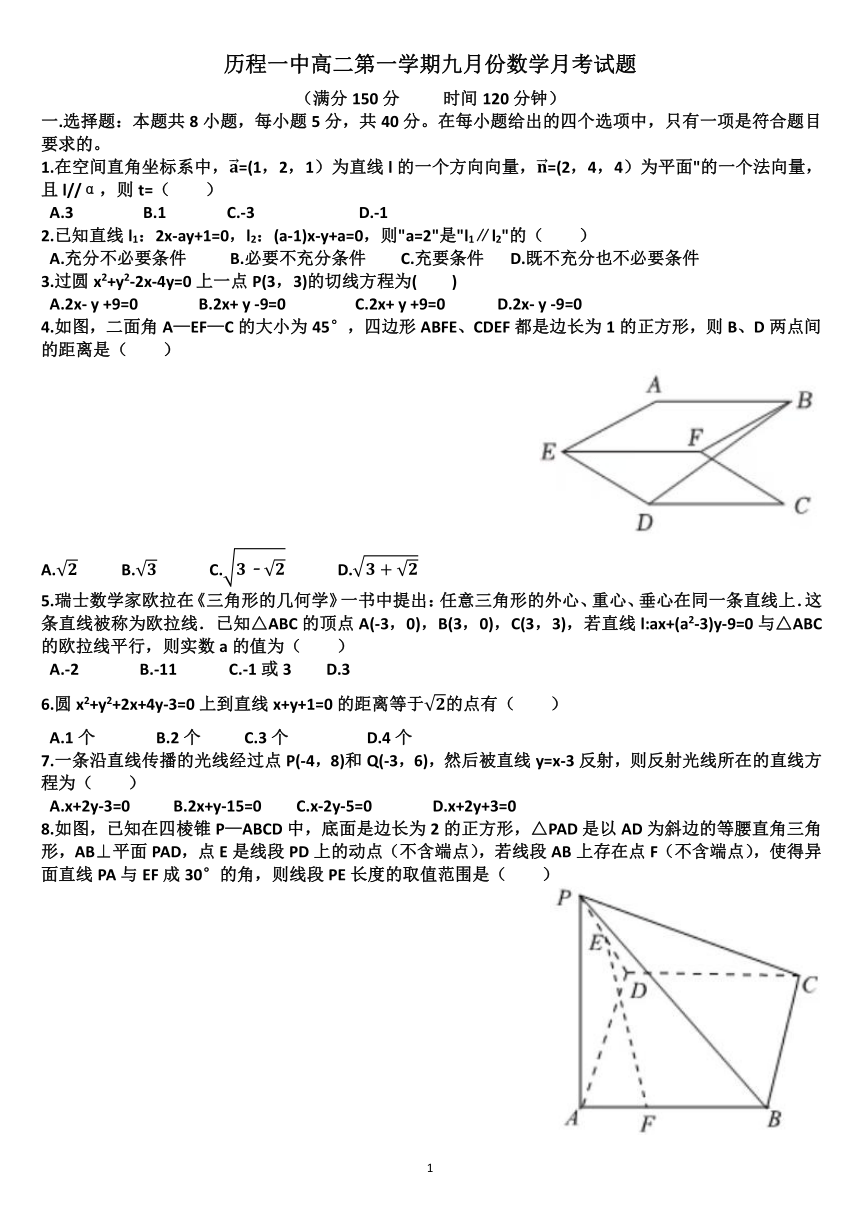 | |
| 格式 | docx | ||
| 文件大小 | 179.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 18:21:18 | ||
图片预览



文档简介
历程一中高二第一学期九月份数学月考试题
(满分150分 时间120分钟)
一.选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,=(1,2,1)为直线l的一个方向向量,=(2,4,4)为平面"的一个法向量,且l//α,则t=( )
A.3 B.1 C.-3 D.-1
2.已知直线l1:2x-ay+1=0,l2:(a-1)x-y+a=0,则"a=2"是"l1∥l2"的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为( )
A.2x- y +9=0 B.2x+ y -9=0 C.2x+ y +9=0 D.2x- y -9=0
4.如图,二面角A—EF—C的大小为45°,四边形ABFE、CDEF都是边长为1的正方形,则B、D两点间的距离是( )
A. B. C. D.
5.瑞士数学家欧拉在《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上.这条直线被称为欧拉线.已知△ABC的顶点A(-3,0),B(3,0),C(3,3),若直线l:ax+(a2-3)y-9=0与△ABC的欧拉线平行,则实数a的值为( )
A.-2 B.-11 C.-1或3 D.3
6.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离等于的点有( )
A.1个 B.2个 C.3个 D.4个
7.一条沿直线传播的光线经过点P(-4,8)和Q(-3,6),然后被直线y=x-3反射,则反射光线所在的直线方程为( )
A.x+2y-3=0 B.2x+y-15=0 C.x-2y-5=0 D.x+2y+3=0
8.如图,已知在四棱锥P—ABCD中,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段PE长度的取值范围是( )
A.(0,) B.(0,) C.(,) D.(,)
二.选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列说法错误的是( )
A.若空间向量∥,则存在唯一的实数,使得=
B.A,B,C三点不共线,空间中任意点O,若=+-+,则P,A,B,C四点共面
C.=(x,2,1),=(4,-2+x,x),与夹角为钝角,则x的取值范围是(﹣,)
D.若(0A,OB,OC)是空间的一个基底,则O,A,B,C四点共面,但不共线
10.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.则下列命题正确的有( )
A.直线l恒过定点(3,1)
B.直线l与圆C恒相交
D.直线l被圆C截得弦长最短时,直线l的方程为2x-y-5=0
11.已知圆C:(x-2)2+y2=1,点P是直线l:x+y=0上一动点,过点P作圆C的切线PA、PB,切点分别是A和B,下列说法正确的( )
A.圆C上恰有一个点到直线l的距离为 B.切线长PA的最小值为1
C.四边形ACBP面积的最小值为2 D.直线AB恒过定点(,﹣)
三.填空题:本题共3小题,每小题5分,共15分。
12.在直线l:2x-y+1=0上一点P到点A(-3,0),B(1,4)两点距离之和最小,则点P的坐标为 .
13.已知直线l过点A(1,2,0),且直线l的一个方向向量为=(0,-1,1),则坐标原点O到直线I的距离d= .
14.已知圆C:x2+y2=4,真线l过点(1,1),把圆分成面积为S1,S2的两部分(S1≥2S2),则的最大值 .
四.解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知△ABC的三个顶点为A(m,n),B(2,1),C(-2,3).
(1)求BC边所在直线的方程;
(2)若BC边上的中线AD所在直线的方程为2x-3y+6=0,且S△ABC=7,求的m,n值.
16.(13分)已知圆C经过点A(3,1),B(-1,3)且圆心C在直线3x-y-2=0上.
(1)求圆C方程;
(2)若E点为圆C上任意一点,且点F(4,0),求线段EF的中点M的轨迹方程.
17.(15分)如图,在三棱柱ABC—A1B1C1中,AA1C1C是边长为4的正方形,AA1B1B为矩形,AB=3,BC=5.
(1)求直线BC与平面A1C1B所成角的正弦值:
(2)证明:在线段BC上是否存在点P,使得P点到平面A1C1B的距离为2,若存在,求BP的值,不存在,请说明理由.
18.(17分)已知圆C:(x-3)2+y2=1与直线m:3x-y+6=0,动直线l过定点4(0,1).
(1)若直线l与圆C相切,求直线l的方程:
(2)若直线l与圆C相交于P、Q两点,点M相交于点N.探索AM和AN是否为定值,若是,求出该定值:若不是,请说明理由。
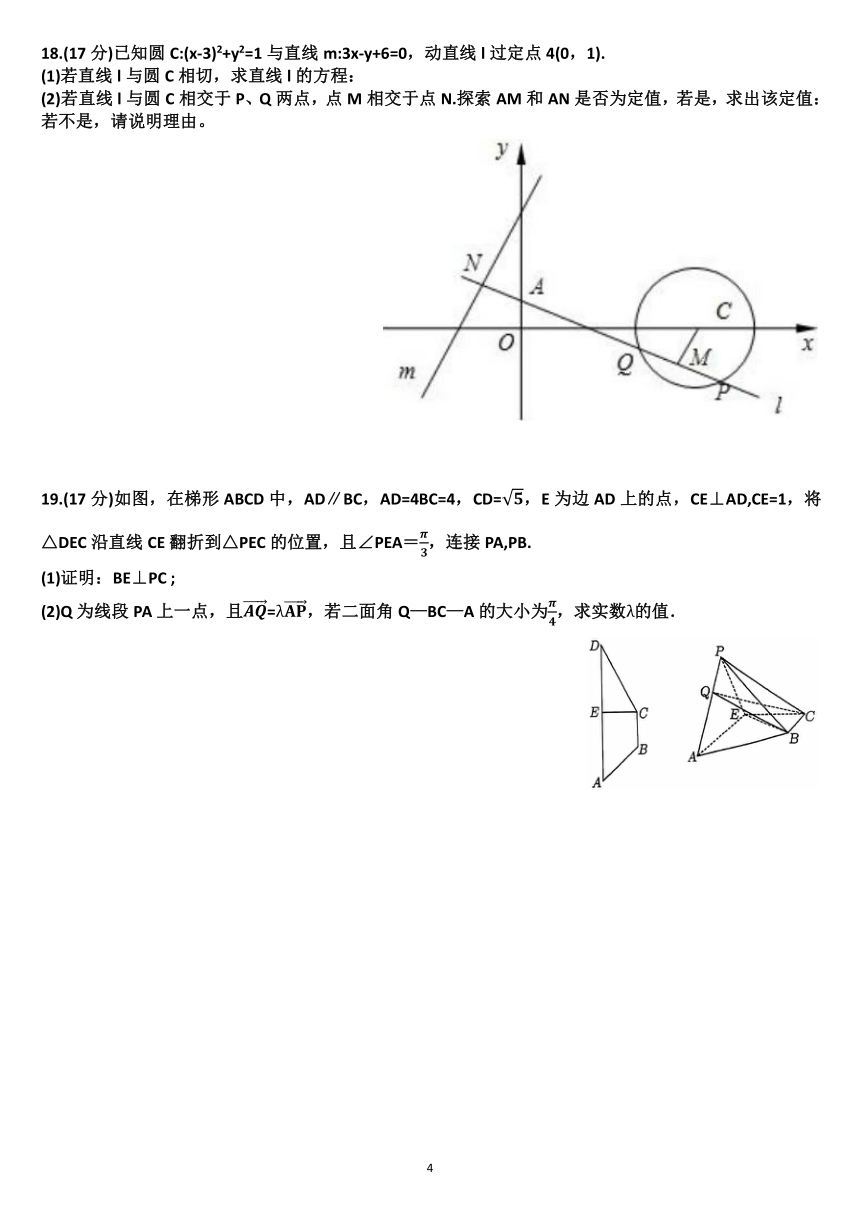
19.(17分)如图,在梯形ABCD中,AD∥BC,AD=4BC=4,CD=,E为边AD上的点,CE⊥AD,CE=1,将△DEC沿直线CE翻折到△PEC的位置,且∠PEA=,连接PA,PB.
(1)证明:BE⊥PC ;
(2)Q为线段PA上一点,且=,若二面角Q—BC—A的大小为,求实数的值.
答案
一.选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,=(1,2,1)为直线l的一个方向向量,=(2,4,4)为平面"的一个法向量,且l//α,则t=( C )
A.3 B.1 C.-3 D.-1
2.已知直线l1:2x-ay+1=0,l2:(a-1)x-y+a=0,则"a=2"是"l1∥l2"的( C )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为( B )
A.2x- y +9=0 B.2x+ y -9=0 C.2x+ y +9=0 D.2x- y -9=0
4.如图,二面角A—EF—C的大小为45°,四边形ABFE、CDEF都是边长为1的正方形,则B、D两点间的距离是( C )
A. B. C. D.
5.瑞士数学家欧拉在《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上.这条直线被称为欧拉线.已知△ABC的顶点A(-3,0),B(3,0),C(3,3),若直线l:ax+(a2-3)y-9=0与△ABC的欧拉线平行,则实数a的值为( B )
A.-2 B.-11 C.-1或3 D.3
6.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离等于的点有( C )
A.1个 B.2个 C.3个 D.4个
7.一条沿直线传播的光线经过点P(-4,8)和Q(-3,6),然后被直线y=x-3反射,则反射光线所在的直线方程为( D )
A.x+2y-3=0 B.2x+y-15=0 C.x-2y-5=0 D.x+2y+3=0
8.如图,已知在四棱锥P—ABCD中,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段PE长度的取值范围是( B )
A.(0,) B.(0,) C.(,) D.(,)
二.选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列说法错误的是( ACD )
A.若空间向量∥,则存在唯一的实数,使得=
B.A,B,C三点不共线,空间中任意点O,若=+-+,则P,A,B,C四点共面
C.=(x,2,1),=(4,-2+x,x),与夹角为钝角,则x的取值范围是(﹣,)
D.若(0A,OB,OC)是空间的一个基底,则O,A,B,C四点共面,但不共线
10.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.则下列命题正确的有( ABD )
A.直线l恒过定点(3,1)
B.直线l与圆C恒相交
D.直线l被圆C截得弦长最短时,直线l的方程为2x-y-5=0
11.已知圆C:(x-2)2+y2=1,点P是直线l:x+y=0上一动点,过点P作圆C的切线PA、PB,切点分别是A和B,下列说法正确的( BD )
A.圆C上恰有一个点到直线l的距离为 B.切线长PA的最小值为1
C.四边形ACBP面积的最小值为2 D.直线AB恒过定点(,﹣)
三.填空题:本题共3小题,每小题5分,共15分。
12.在直线l:2x-y+1=0上一点P到点A(-3,0),B(1,4)两点距离之和最小,则点P的坐标为 (1,3) .
13.已知直线l过点A(1,2,0),且直线l的一个方向向量为=(0,-1,1),则坐标原点O到直线I的距离d= .
14.已知圆C:x2+y2=4,真线l过点(1,1),把圆分成面积为S1,S2的两部分(S1≥2S2),则的最大值 .
四.解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知△ABC的三个顶点为A(m,n),B(2,1),C(-2,3).
(1)求BC边所在直线的方程;
(2)若BC边上的中线AD所在直线的方程为2x-3y+6=0,且S△ABC=7,求的m,n值.
(1)x+2y﹣4=0
(2)m=3,n=4或m=﹣3,n=0
16.(13分)已知圆C经过点A(3,1),B(-1,3)且圆心C在直线3x-y-2=0上.
(1)求圆C方程;
(2)若E点为圆C上任意一点,且点F(4,0),求线段EF的中点M的轨迹方程.
(1)(x﹣2)2+(y﹣4)2=10
(2)(x﹣3)2+(y﹣2)2=
17.(15分)如图,在三棱柱ABC—A1B1C1中,AA1C1C是边长为4的正方形,AA1B1B为矩形,AB=3,BC=5.
(1)求直线BC与平面A1C1B所成角的正弦值:
(2)证明:在线段BC上是否存在点P,使得P点到平面A1C1B的距离为2,若存在,求BP的值,不存在,请说明理由.
(1)
(2)
18.(17分)已知圆C:(x-3)2+y2=1与直线m:3x-y+6=0,动直线l过定点4(0,1).
(1)若直线l与圆C相切,求直线l的方程:
(2)若直线l与圆C相交于P、Q两点,点M相交于点N.探索AM和AN是否为定值,若是,求出该定值:若不是,请说明理由。
(1)y=1或y=﹣x+1
(2)是定值为﹣5
19.(17分)如图,在梯形ABCD中,AD∥BC,AD=4BC=4,CD=,E为边AD上的点,CE⊥AD,CE=1,将△DEC沿直线CE翻折到△PEC的位置,且∠PEA=,连接PA,PB.
(1)证明:BE⊥PC ;
(2)Q为线段PA上一点,且=,若二面角Q—BC—A的大小为,求实数的值.
(1)略
(2)
(满分150分 时间120分钟)
一.选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,=(1,2,1)为直线l的一个方向向量,=(2,4,4)为平面"的一个法向量,且l//α,则t=( )
A.3 B.1 C.-3 D.-1
2.已知直线l1:2x-ay+1=0,l2:(a-1)x-y+a=0,则"a=2"是"l1∥l2"的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为( )
A.2x- y +9=0 B.2x+ y -9=0 C.2x+ y +9=0 D.2x- y -9=0
4.如图,二面角A—EF—C的大小为45°,四边形ABFE、CDEF都是边长为1的正方形,则B、D两点间的距离是( )
A. B. C. D.
5.瑞士数学家欧拉在《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上.这条直线被称为欧拉线.已知△ABC的顶点A(-3,0),B(3,0),C(3,3),若直线l:ax+(a2-3)y-9=0与△ABC的欧拉线平行,则实数a的值为( )
A.-2 B.-11 C.-1或3 D.3
6.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离等于的点有( )
A.1个 B.2个 C.3个 D.4个
7.一条沿直线传播的光线经过点P(-4,8)和Q(-3,6),然后被直线y=x-3反射,则反射光线所在的直线方程为( )
A.x+2y-3=0 B.2x+y-15=0 C.x-2y-5=0 D.x+2y+3=0
8.如图,已知在四棱锥P—ABCD中,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段PE长度的取值范围是( )
A.(0,) B.(0,) C.(,) D.(,)
二.选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列说法错误的是( )
A.若空间向量∥,则存在唯一的实数,使得=
B.A,B,C三点不共线,空间中任意点O,若=+-+,则P,A,B,C四点共面
C.=(x,2,1),=(4,-2+x,x),与夹角为钝角,则x的取值范围是(﹣,)
D.若(0A,OB,OC)是空间的一个基底,则O,A,B,C四点共面,但不共线
10.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.则下列命题正确的有( )
A.直线l恒过定点(3,1)
B.直线l与圆C恒相交
D.直线l被圆C截得弦长最短时,直线l的方程为2x-y-5=0
11.已知圆C:(x-2)2+y2=1,点P是直线l:x+y=0上一动点,过点P作圆C的切线PA、PB,切点分别是A和B,下列说法正确的( )
A.圆C上恰有一个点到直线l的距离为 B.切线长PA的最小值为1
C.四边形ACBP面积的最小值为2 D.直线AB恒过定点(,﹣)
三.填空题:本题共3小题,每小题5分,共15分。
12.在直线l:2x-y+1=0上一点P到点A(-3,0),B(1,4)两点距离之和最小,则点P的坐标为 .
13.已知直线l过点A(1,2,0),且直线l的一个方向向量为=(0,-1,1),则坐标原点O到直线I的距离d= .
14.已知圆C:x2+y2=4,真线l过点(1,1),把圆分成面积为S1,S2的两部分(S1≥2S2),则的最大值 .
四.解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知△ABC的三个顶点为A(m,n),B(2,1),C(-2,3).
(1)求BC边所在直线的方程;
(2)若BC边上的中线AD所在直线的方程为2x-3y+6=0,且S△ABC=7,求的m,n值.
16.(13分)已知圆C经过点A(3,1),B(-1,3)且圆心C在直线3x-y-2=0上.
(1)求圆C方程;
(2)若E点为圆C上任意一点,且点F(4,0),求线段EF的中点M的轨迹方程.
17.(15分)如图,在三棱柱ABC—A1B1C1中,AA1C1C是边长为4的正方形,AA1B1B为矩形,AB=3,BC=5.
(1)求直线BC与平面A1C1B所成角的正弦值:
(2)证明:在线段BC上是否存在点P,使得P点到平面A1C1B的距离为2,若存在,求BP的值,不存在,请说明理由.
18.(17分)已知圆C:(x-3)2+y2=1与直线m:3x-y+6=0,动直线l过定点4(0,1).
(1)若直线l与圆C相切,求直线l的方程:
(2)若直线l与圆C相交于P、Q两点,点M相交于点N.探索AM和AN是否为定值,若是,求出该定值:若不是,请说明理由。
19.(17分)如图,在梯形ABCD中,AD∥BC,AD=4BC=4,CD=,E为边AD上的点,CE⊥AD,CE=1,将△DEC沿直线CE翻折到△PEC的位置,且∠PEA=,连接PA,PB.
(1)证明:BE⊥PC ;
(2)Q为线段PA上一点,且=,若二面角Q—BC—A的大小为,求实数的值.
答案
一.选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在空间直角坐标系中,=(1,2,1)为直线l的一个方向向量,=(2,4,4)为平面"的一个法向量,且l//α,则t=( C )
A.3 B.1 C.-3 D.-1
2.已知直线l1:2x-ay+1=0,l2:(a-1)x-y+a=0,则"a=2"是"l1∥l2"的( C )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为( B )
A.2x- y +9=0 B.2x+ y -9=0 C.2x+ y +9=0 D.2x- y -9=0
4.如图,二面角A—EF—C的大小为45°,四边形ABFE、CDEF都是边长为1的正方形,则B、D两点间的距离是( C )
A. B. C. D.
5.瑞士数学家欧拉在《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上.这条直线被称为欧拉线.已知△ABC的顶点A(-3,0),B(3,0),C(3,3),若直线l:ax+(a2-3)y-9=0与△ABC的欧拉线平行,则实数a的值为( B )
A.-2 B.-11 C.-1或3 D.3
6.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离等于的点有( C )
A.1个 B.2个 C.3个 D.4个
7.一条沿直线传播的光线经过点P(-4,8)和Q(-3,6),然后被直线y=x-3反射,则反射光线所在的直线方程为( D )
A.x+2y-3=0 B.2x+y-15=0 C.x-2y-5=0 D.x+2y+3=0
8.如图,已知在四棱锥P—ABCD中,底面是边长为2的正方形,△PAD是以AD为斜边的等腰直角三角形,AB⊥平面PAD,点E是线段PD上的动点(不含端点),若线段AB上存在点F(不含端点),使得异面直线PA与EF成30°的角,则线段PE长度的取值范围是( B )
A.(0,) B.(0,) C.(,) D.(,)
二.选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列说法错误的是( ACD )
A.若空间向量∥,则存在唯一的实数,使得=
B.A,B,C三点不共线,空间中任意点O,若=+-+,则P,A,B,C四点共面
C.=(x,2,1),=(4,-2+x,x),与夹角为钝角,则x的取值范围是(﹣,)
D.若(0A,OB,OC)是空间的一个基底,则O,A,B,C四点共面,但不共线
10.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.则下列命题正确的有( ABD )
A.直线l恒过定点(3,1)
B.直线l与圆C恒相交
D.直线l被圆C截得弦长最短时,直线l的方程为2x-y-5=0
11.已知圆C:(x-2)2+y2=1,点P是直线l:x+y=0上一动点,过点P作圆C的切线PA、PB,切点分别是A和B,下列说法正确的( BD )
A.圆C上恰有一个点到直线l的距离为 B.切线长PA的最小值为1
C.四边形ACBP面积的最小值为2 D.直线AB恒过定点(,﹣)
三.填空题:本题共3小题,每小题5分,共15分。
12.在直线l:2x-y+1=0上一点P到点A(-3,0),B(1,4)两点距离之和最小,则点P的坐标为 (1,3) .
13.已知直线l过点A(1,2,0),且直线l的一个方向向量为=(0,-1,1),则坐标原点O到直线I的距离d= .
14.已知圆C:x2+y2=4,真线l过点(1,1),把圆分成面积为S1,S2的两部分(S1≥2S2),则的最大值 .
四.解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知△ABC的三个顶点为A(m,n),B(2,1),C(-2,3).
(1)求BC边所在直线的方程;
(2)若BC边上的中线AD所在直线的方程为2x-3y+6=0,且S△ABC=7,求的m,n值.
(1)x+2y﹣4=0
(2)m=3,n=4或m=﹣3,n=0
16.(13分)已知圆C经过点A(3,1),B(-1,3)且圆心C在直线3x-y-2=0上.
(1)求圆C方程;
(2)若E点为圆C上任意一点,且点F(4,0),求线段EF的中点M的轨迹方程.
(1)(x﹣2)2+(y﹣4)2=10
(2)(x﹣3)2+(y﹣2)2=
17.(15分)如图,在三棱柱ABC—A1B1C1中,AA1C1C是边长为4的正方形,AA1B1B为矩形,AB=3,BC=5.
(1)求直线BC与平面A1C1B所成角的正弦值:
(2)证明:在线段BC上是否存在点P,使得P点到平面A1C1B的距离为2,若存在,求BP的值,不存在,请说明理由.
(1)
(2)
18.(17分)已知圆C:(x-3)2+y2=1与直线m:3x-y+6=0,动直线l过定点4(0,1).
(1)若直线l与圆C相切,求直线l的方程:
(2)若直线l与圆C相交于P、Q两点,点M相交于点N.探索AM和AN是否为定值,若是,求出该定值:若不是,请说明理由。
(1)y=1或y=﹣x+1
(2)是定值为﹣5
19.(17分)如图,在梯形ABCD中,AD∥BC,AD=4BC=4,CD=,E为边AD上的点,CE⊥AD,CE=1,将△DEC沿直线CE翻折到△PEC的位置,且∠PEA=,连接PA,PB.
(1)证明:BE⊥PC ;
(2)Q为线段PA上一点,且=,若二面角Q—BC—A的大小为,求实数的值.
(1)略
(2)
同课章节目录
