选择必修 第三章 3.2.2 双曲线的简单几何性质(第2课时)课件(共26张PPT)
文档属性
| 名称 | 选择必修 第三章 3.2.2 双曲线的简单几何性质(第2课时)课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-10-17 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
选择必修
第三章 圆锥曲线的方程
3.2 双曲线
3.2.2 双曲线的简单几何性质(第2课时)
教学目标
学习目标 数学素养
1.进一步掌握双曲线的方程及其简单几何性质的应用. 1.数学抽象素养和逻辑推理素养.
2.进一步掌握与双曲线有关的点的轨迹问题的求解方法. 2.数学抽象素养和数学运算素养.
3.会判断直线与双曲线的位置关系,并求解其相关问题. 3.数学运算素养和逻辑推理素养.
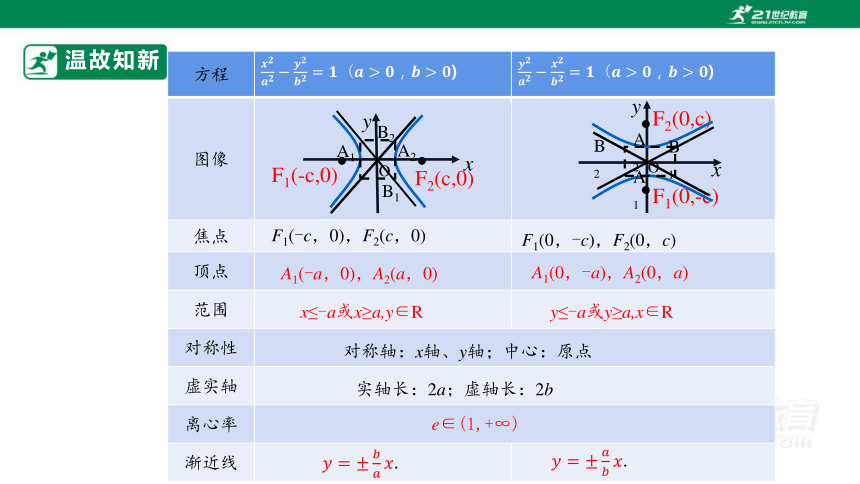
温故知新
方程 ) )
图像
焦点
顶点
范围
对称性 虚实轴 离心率 渐近线
F1(-c,0)
F2(c,0)
.
.
y
B2
A1
A2
B1
x
O
F2(0,c)
F1(0,-c)
x
B1
y
O
.
B2
A1
A2
.
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
x≤-a或x≥a,y∈R
y≤-a或y≥a,x∈R
对称轴:x轴、y轴;中心:原点
实轴长:2a;虚轴长:2b
e∈(1,+∞)
.
.
知新引入
【例1】双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(如右图),它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试建立适当的坐标系,求出双曲线的方程(精确到1m).
分析:本题建立适当的坐标系是关键.注意到通风塔有三个特殊的截口圆:上口、下口、最小的一个截口.显然,最小截口圆的圆心是双曲线的中心,直径是双曲线的实轴,所以以最小截口直径所在直线为x轴,圆心为原点建立坐标系,则双曲线的方程具有最简单的形式.
知新引入
【例1】双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(如右图),它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试建立适当的坐标系,求出双曲线的方程(精确到1m).
解:
根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示直角坐标系Oxy,使小圆的直径A′A在轴x上,圆心与原点重合.
设双曲线的方程为,点C的坐标为(13,y),
这时,上、下口的直径CC′、BB′都平行于x轴,且|CC′|=13×2,|BB′|=25×2.
又B,C两点都在双曲线上,所以
.
则点B的坐标为(25,55-y).因为直径A′A是实轴,所以a=12.
知新引入
【例1】双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(如右图),它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试建立适当的坐标系,求出双曲线的方程(精确到1m).
解:
由方程②,得(负值舍去),代入方程①,得
化简,得19b2+275b-18150=0 ③
.
因此所求双曲线的方程为.
解方程③,得b≈25(负值舍去).
.
初试身手
1.飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记为A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°方向,相距4千米,P为航天员着陆点.某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒,求在A处发现P的方向角.
由题意知|PC|=|PB|,所以P的运动轨迹在线段BC的垂直平分线上.
解:
又∵|PB|-|PA|=4<6=|AB|,
∴P在以A,B为焦点的双曲线的靠近A的一支上.
以线段AB的中点为坐标原点,AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,如图所示.
则A(3,0),B(-3,0),C(-5,2),a=2,c=3,b2=c2-a2=5
∴点P所在双曲线右支的方程为(x≥2),①
初试身手
1.飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记为A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°方向,相距4千米,P为航天员着陆点.某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒,求在A处发现P的方向角.
BC的垂直平分线的方程为x-y+7=0. ②
解:
∴∠PAx=60°,所以P点在A点的东偏北60°方向.
由①②得x=8,y=5,
则A(3,0),B(-3,0),C(-5,2),a=2,c=3,b2=c2-a2=5
∴点P所在双曲线右支的方程为(x≥2),①
∴P(8,5),kPA=,
知新探究
【例2】动点M(x,y)与定点F(4,0)的距离和它到定直线l:x=的距离的比是常数,求动点M的轨迹.
解:
设d是点M到直线l的距离,根据题意,动点M的轨迹就是点的集合
P={M|}.
由此得 .
7x2-9y2=63,
将上式两边平方,并化简,得
即 .
∴点M的轨迹是焦点在x轴上,实轴长为6,虚轴长为的双曲线的右支(如图).
知新探究
拓展:
若动点M(x,y)与定点F(c,0)的距离和它到定直线l:的距离比是常数,则点M的轨迹是双曲线.其中定点F(c,0)是焦点,定直线l:相应于F的准线;另一焦点F′(-c,0),相应于的准线l′:.
这就是双曲线的第二定义.
将例2与椭圆一节中的例6比较,你有什么发现?
若动点M(x,y)与定点F(c,0)的距离和它到定直线l:的距离比是常数,
若a>c>0即0若c>a>0即e>1,则点M的轨迹是焦点在x轴上的双曲线.
知新探究
【例3】已知直线y=kx+1与双曲线3x2-y2=1相交于A,B两点,当k为何值时,A,B在双曲线的同一支上 当k为何值时,A,B分别在双曲线的两支上
解:
把y=kx+1代入3x2-y2=1,整理,得(3-k2)x2-2kx-2=0.
则需满足k≠±,且Δ=24-4k2>0.
由Δ>0,解得-分析:直线与双曲线有两交点的条件是联立后的方程有两组解,也就是消元后获得的一元二次方程有两解.两交点在同一支上,则说明两个交点的横坐标同号,即一元二次方程有两个同号的实数根,两交点分别在两支上,则说明两个交点的横坐标异号,即一元二次方程有两个异号的实数根.
设A(x1,y1),B(x2,y2),要使直线与双曲线有两个交点,
知新探究
【例3】已知直线y=kx+1与双曲线3x2-y2=1相交于A,B两点,当k为何值时,A,B在双曲线的同一支上 当k为何值时,A,B分别在双曲线的两支上
解:
把y=kx+1代入3x2-y2=1,整理,得(3-k2)x2-2kx-2=0.
若A,B在双曲线的同一支上,则需,解得;
若A,B分别在双曲线的两支上,则需,解得.
设A(x1,y1),B(x2,y2),
所以,当时,A,B两点在双曲线的同一支上;
当时,A,B两点在双曲线的两支上.
知新探究
直线与双曲线的位置关系
1.相离:没有交点;
2.相切:1个交点(不与渐近线平行);
3.相交:
⑴1个交点(与渐近线平行);
⑵2个交点(两交点可在同一支,也可在不同支).
当l与渐近线平行,与双曲线相交且1个交点
当l倾斜角小于渐近线倾斜角,与双曲线相交且两个交点在不同支
当l倾斜角大于渐近线倾斜角,与双曲线相交且两个交点在同一支
知新探究
判断直线与双曲线位置关系的基本步骤
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线斜率相等
相交(一个交点)或相离
计 算 判 别 式
Δ>0
Δ=0
Δ<0
相交
相切
相离
二次项系数为0
二次项系数不为0
初试身手
2.已知直线l:y=kx-1与双曲线C:x2-y2=4.
⑴若直线l与双曲线C有两个不同的交点,求实数k的取值范围;
⑵若直线l与双曲线C只有一个交点,求实数k的取值范围.
解:
⑴此时等价于方程①有两个不等实根,则
由得(1-k2)x2+2kx-5=0 ①.
,
解得,
解得.
⑵此时等价于方程①只有一解.
当1-k2=0,即k=±1时,方程①只有一解;
当1-k2≠0时,应满足Δ=4k2+20(1-k2)=0,
故k的值为±1或.
知新探究
【例4】如图,过双曲线=1的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,求|AB|.
解:
方法1:由双曲线的标准方程可知,双曲线的焦点分别为F1(-3,0),F2(3,0).
∵因为直线AB的倾斜角是30°,且经过右焦点F2,
由消去y,得5x2+6x-27=0,解得x1=-3,x2=,
将x1,x2的值分别代入①,得.
∴|AB|=.
于是,A,B两点的坐标分别为.
∴所以直线AB的方程为.①
知新探究
【例4】如图,过双曲线=1的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,求|AB|.
解:
方法2:设A,B两点的坐标分别为(x1,y1),(x2,y2),
则由根与系数关系,得
.
∴|AB|=.
由方法1直线与双曲线联立,得5x2+6x-27=0,
知新探究
设斜率为k(k≠0)的直线l与双曲线相交于A(x1,y1),B(x2,y2)两点,则
⑴|AB|=;
⑵|AB|=|x1-x2|或|AB|=|y1-y2|.
直线与双曲线相交的弦长公式
初试身手
3.过双曲线的左焦点F1,作倾斜角为的直线AB,其中A,B分别为直线与双曲线的交点,求线段AB的长.
解:
由题意得,左焦点F1的坐标为(-2,0),
∵直线AB的倾斜角为,
∴直线AB的方程为y=x+2,
由,消去y,得2x2-4x-7=0,
∴x1+x2=-2,x1x2=.
则|AB|=.
显然Δ>0,设A(x1,y1),B(x2,y2),
知新探究
【例5】经过点M(2,2)作直线l交双曲线于A,B两点,且M为AB的中点.
⑴求直线l的方程; ⑵求线段AB的长.
解:
⑴设A(x1,y1),B(x2,y2),代入双曲线方程得,
两式相减得,
即,
∵M为AB的中点,
∴x1+x2=4,y1+y2=4,
经检验k=4符合题意.
∴l的方程为y-2=4(x-2),即y=4x-6.
∴4(x1-x2)-(y1-y2)=0,.
⑵将y=4x-6代入中得3x2-12x+10=0,
∴x1+x2=4,x1x2=,
则|AB|=.
初试身手
4.已知双曲线,求过点A(3,-1)且被点A平分的弦MN所在直线的方程.
解:
由,消去y,整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),则x1+x2=,
∴所求直线MN的方程为y+1=(x-3),即3x+4y-5=0.
当时,满足Δ>0,符合题意,
∵A(3,-1)平分弦MN,
解得,
∴ ,即,
方法1:由题意知直线的斜率存在,故可设直线方程为y+1=k(x-3),即y=kx-3k-1,
初试身手
4.已知双曲线,求过点A(3,-1)且被点A平分的弦MN所在直线的方程.
解:
∵M,N均在双曲线上,
∴,
∴所求直线MN的方程为y+1=(x-3),即3x+4y-5=0.
经验证,该直线MN存在.
两式相减得,
方法2:设M(x1,y1),N(x2,y2),
即,
∵A(3,-1)平分弦MN,
∴x1+x2=6,y1+y2=-2,
∴3(x1-x2)+4(y1-y2)=0,.
作业布置
作业:
P127-128 习题3.2 第5,10,11,13,14题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修
第三章 圆锥曲线的方程
3.2 双曲线
3.2.2 双曲线的简单几何性质(第2课时)
教学目标
学习目标 数学素养
1.进一步掌握双曲线的方程及其简单几何性质的应用. 1.数学抽象素养和逻辑推理素养.
2.进一步掌握与双曲线有关的点的轨迹问题的求解方法. 2.数学抽象素养和数学运算素养.
3.会判断直线与双曲线的位置关系,并求解其相关问题. 3.数学运算素养和逻辑推理素养.
温故知新
方程 ) )
图像
焦点
顶点
范围
对称性 虚实轴 离心率 渐近线
F1(-c,0)
F2(c,0)
.
.
y
B2
A1
A2
B1
x
O
F2(0,c)
F1(0,-c)
x
B1
y
O
.
B2
A1
A2
.
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
x≤-a或x≥a,y∈R
y≤-a或y≥a,x∈R
对称轴:x轴、y轴;中心:原点
实轴长:2a;虚轴长:2b
e∈(1,+∞)
.
.
知新引入
【例1】双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(如右图),它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试建立适当的坐标系,求出双曲线的方程(精确到1m).
分析:本题建立适当的坐标系是关键.注意到通风塔有三个特殊的截口圆:上口、下口、最小的一个截口.显然,最小截口圆的圆心是双曲线的中心,直径是双曲线的实轴,所以以最小截口直径所在直线为x轴,圆心为原点建立坐标系,则双曲线的方程具有最简单的形式.
知新引入
【例1】双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(如右图),它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试建立适当的坐标系,求出双曲线的方程(精确到1m).
解:
根据双曲线的对称性,在冷却塔的轴截面所在平面建立如图所示直角坐标系Oxy,使小圆的直径A′A在轴x上,圆心与原点重合.
设双曲线的方程为,点C的坐标为(13,y),
这时,上、下口的直径CC′、BB′都平行于x轴,且|CC′|=13×2,|BB′|=25×2.
又B,C两点都在双曲线上,所以
.
则点B的坐标为(25,55-y).因为直径A′A是实轴,所以a=12.
知新引入
【例1】双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(如右图),它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试建立适当的坐标系,求出双曲线的方程(精确到1m).
解:
由方程②,得(负值舍去),代入方程①,得
化简,得19b2+275b-18150=0 ③
.
因此所求双曲线的方程为.
解方程③,得b≈25(负值舍去).
.
初试身手
1.飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记为A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°方向,相距4千米,P为航天员着陆点.某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒,求在A处发现P的方向角.
由题意知|PC|=|PB|,所以P的运动轨迹在线段BC的垂直平分线上.
解:
又∵|PB|-|PA|=4<6=|AB|,
∴P在以A,B为焦点的双曲线的靠近A的一支上.
以线段AB的中点为坐标原点,AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,如图所示.
则A(3,0),B(-3,0),C(-5,2),a=2,c=3,b2=c2-a2=5
∴点P所在双曲线右支的方程为(x≥2),①
初试身手
1.飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记为A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°方向,相距4千米,P为航天员着陆点.某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,在此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒,求在A处发现P的方向角.
BC的垂直平分线的方程为x-y+7=0. ②
解:
∴∠PAx=60°,所以P点在A点的东偏北60°方向.
由①②得x=8,y=5,
则A(3,0),B(-3,0),C(-5,2),a=2,c=3,b2=c2-a2=5
∴点P所在双曲线右支的方程为(x≥2),①
∴P(8,5),kPA=,
知新探究
【例2】动点M(x,y)与定点F(4,0)的距离和它到定直线l:x=的距离的比是常数,求动点M的轨迹.
解:
设d是点M到直线l的距离,根据题意,动点M的轨迹就是点的集合
P={M|}.
由此得 .
7x2-9y2=63,
将上式两边平方,并化简,得
即 .
∴点M的轨迹是焦点在x轴上,实轴长为6,虚轴长为的双曲线的右支(如图).
知新探究
拓展:
若动点M(x,y)与定点F(c,0)的距离和它到定直线l:的距离比是常数,则点M的轨迹是双曲线.其中定点F(c,0)是焦点,定直线l:相应于F的准线;另一焦点F′(-c,0),相应于的准线l′:.
这就是双曲线的第二定义.
将例2与椭圆一节中的例6比较,你有什么发现?
若动点M(x,y)与定点F(c,0)的距离和它到定直线l:的距离比是常数,
若a>c>0即0
知新探究
【例3】已知直线y=kx+1与双曲线3x2-y2=1相交于A,B两点,当k为何值时,A,B在双曲线的同一支上 当k为何值时,A,B分别在双曲线的两支上
解:
把y=kx+1代入3x2-y2=1,整理,得(3-k2)x2-2kx-2=0.
则需满足k≠±,且Δ=24-4k2>0.
由Δ>0,解得-
设A(x1,y1),B(x2,y2),要使直线与双曲线有两个交点,
知新探究
【例3】已知直线y=kx+1与双曲线3x2-y2=1相交于A,B两点,当k为何值时,A,B在双曲线的同一支上 当k为何值时,A,B分别在双曲线的两支上
解:
把y=kx+1代入3x2-y2=1,整理,得(3-k2)x2-2kx-2=0.
若A,B在双曲线的同一支上,则需,解得;
若A,B分别在双曲线的两支上,则需,解得.
设A(x1,y1),B(x2,y2),
所以,当时,A,B两点在双曲线的同一支上;
当时,A,B两点在双曲线的两支上.
知新探究
直线与双曲线的位置关系
1.相离:没有交点;
2.相切:1个交点(不与渐近线平行);
3.相交:
⑴1个交点(与渐近线平行);
⑵2个交点(两交点可在同一支,也可在不同支).
当l与渐近线平行,与双曲线相交且1个交点
当l倾斜角小于渐近线倾斜角,与双曲线相交且两个交点在不同支
当l倾斜角大于渐近线倾斜角,与双曲线相交且两个交点在同一支
知新探究
判断直线与双曲线位置关系的基本步骤
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线斜率相等
相交(一个交点)或相离
计 算 判 别 式
Δ>0
Δ=0
Δ<0
相交
相切
相离
二次项系数为0
二次项系数不为0
初试身手
2.已知直线l:y=kx-1与双曲线C:x2-y2=4.
⑴若直线l与双曲线C有两个不同的交点,求实数k的取值范围;
⑵若直线l与双曲线C只有一个交点,求实数k的取值范围.
解:
⑴此时等价于方程①有两个不等实根,则
由得(1-k2)x2+2kx-5=0 ①.
,
解得,
解得.
⑵此时等价于方程①只有一解.
当1-k2=0,即k=±1时,方程①只有一解;
当1-k2≠0时,应满足Δ=4k2+20(1-k2)=0,
故k的值为±1或.
知新探究
【例4】如图,过双曲线=1的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,求|AB|.
解:
方法1:由双曲线的标准方程可知,双曲线的焦点分别为F1(-3,0),F2(3,0).
∵因为直线AB的倾斜角是30°,且经过右焦点F2,
由消去y,得5x2+6x-27=0,解得x1=-3,x2=,
将x1,x2的值分别代入①,得.
∴|AB|=.
于是,A,B两点的坐标分别为.
∴所以直线AB的方程为.①
知新探究
【例4】如图,过双曲线=1的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,求|AB|.
解:
方法2:设A,B两点的坐标分别为(x1,y1),(x2,y2),
则由根与系数关系,得
.
∴|AB|=.
由方法1直线与双曲线联立,得5x2+6x-27=0,
知新探究
设斜率为k(k≠0)的直线l与双曲线相交于A(x1,y1),B(x2,y2)两点,则
⑴|AB|=;
⑵|AB|=|x1-x2|或|AB|=|y1-y2|.
直线与双曲线相交的弦长公式
初试身手
3.过双曲线的左焦点F1,作倾斜角为的直线AB,其中A,B分别为直线与双曲线的交点,求线段AB的长.
解:
由题意得,左焦点F1的坐标为(-2,0),
∵直线AB的倾斜角为,
∴直线AB的方程为y=x+2,
由,消去y,得2x2-4x-7=0,
∴x1+x2=-2,x1x2=.
则|AB|=.
显然Δ>0,设A(x1,y1),B(x2,y2),
知新探究
【例5】经过点M(2,2)作直线l交双曲线于A,B两点,且M为AB的中点.
⑴求直线l的方程; ⑵求线段AB的长.
解:
⑴设A(x1,y1),B(x2,y2),代入双曲线方程得,
两式相减得,
即,
∵M为AB的中点,
∴x1+x2=4,y1+y2=4,
经检验k=4符合题意.
∴l的方程为y-2=4(x-2),即y=4x-6.
∴4(x1-x2)-(y1-y2)=0,.
⑵将y=4x-6代入中得3x2-12x+10=0,
∴x1+x2=4,x1x2=,
则|AB|=.
初试身手
4.已知双曲线,求过点A(3,-1)且被点A平分的弦MN所在直线的方程.
解:
由,消去y,整理得(1-4k2)x2+8k(3k+1)x-36k2-24k-8=0.
设M(x1,y1),N(x2,y2),则x1+x2=,
∴所求直线MN的方程为y+1=(x-3),即3x+4y-5=0.
当时,满足Δ>0,符合题意,
∵A(3,-1)平分弦MN,
解得,
∴ ,即,
方法1:由题意知直线的斜率存在,故可设直线方程为y+1=k(x-3),即y=kx-3k-1,
初试身手
4.已知双曲线,求过点A(3,-1)且被点A平分的弦MN所在直线的方程.
解:
∵M,N均在双曲线上,
∴,
∴所求直线MN的方程为y+1=(x-3),即3x+4y-5=0.
经验证,该直线MN存在.
两式相减得,
方法2:设M(x1,y1),N(x2,y2),
即,
∵A(3,-1)平分弦MN,
∴x1+x2=6,y1+y2=-2,
∴3(x1-x2)+4(y1-y2)=0,.
作业布置
作业:
P127-128 习题3.2 第5,10,11,13,14题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
