垂直于弦的直径课件
图片预览








文档简介
课件21张PPT。九台三十一中学你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶。它的主桥是圆弧形,它的跨度(弧所对的弦长)为
37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?问题探究用纸剪一个圆,沿着圆的任意
一条直径对折,重复做几次,
你发现了什么?由此你得到了
什么
结论? 圆是轴对称图形,任何一条直
径所在直线都是它的对称轴。结论:如图,AB是圆O的一条弦,作直径CD,
使CD⊥AB,垂足为E.(1)此图是轴对称图
形吗?如果是,它
的对称轴是什么?(2)你能发现图中有哪
些相等的线段和弧?为什么?已知:在⊙o中,CD是直径,AB是弦,CD⊥AB,垂足为E证明:连结OA,OB则OA=OB∵垂直于弦的直径CD所在的直线
既是等腰△OAB的对称轴,
又是⊙O的对称轴∴当把圆沿着直径CD折叠时,
CD两侧的两个半圆重合还有其它方法吗?垂径定理:垂直于弦的直径平分这条弦,
并平分这条弦所对的两条弧问题:此定理的条件和结论分别是什么?推论:1.平分弦(不是直径)的直径垂直于
弦,并且平分弦所对的两条弧。
2.平分弧的直径垂直平分这条弧所对的弦推广:(1)过圆心的直线
(2)垂直弦 (3)平分弦
(4)平分优弧
(5)平分劣弧
由其中两个条件可推出
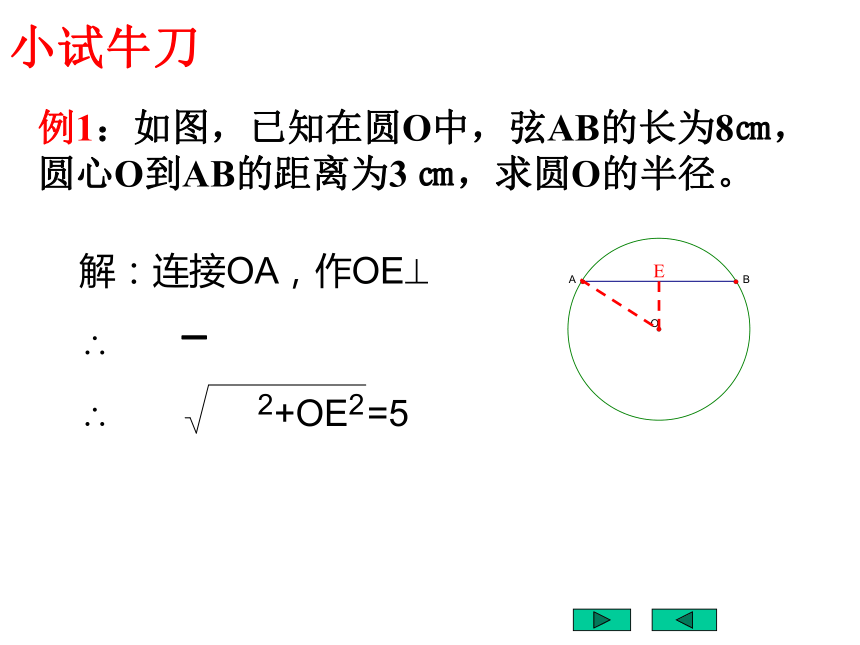
另外三个结论。5.2.3定理小试牛刀例1:如图,已知在圆O中,弦AB的长为8㎝,
圆心O到AB的距离为3 ㎝,求圆O的半径。现在我们
来解释桥
的问题吧答:赵州桥主桥半径约为27.9m.驶向胜利的彼岸挑战自我1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )√???√ 2.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?证明:相等。理由:
过O作OE⊥AB,垂足为E,
∴AE=BE,CE=DE。
∴ AE-CE=BE-DE
∴AC=BD注意:解决有关弦的问题,过圆心作弦的垂线,是一种常用的辅助线添法.CDABE.平分已知弧AB已知:AB
作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:AB的中点⌒⌒你能破镜重圆吗?ABACmn·O 1.作弦AB.AC及它们的垂直平分线m.n,交于O点; 2.以O为圆心,OA为半径作圆。你能破镜重圆吗?ABACmn·O 1.作弦AB.AC及它们的垂直平分线m.n,交于O点; 2.以O为圆心,OA为半径作圆。练习1:在半径为50㎜的圆O中,有长50㎜的
弦AB,计算:
⑴点O与AB的距离;
⑵∠AOB的度数。练习2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。垂径定理的应用 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. 反思:在⊙ O中,若⊙ O的半径r、
圆心到弦的距离d、弦长a中,
任意知道两个量,可根据 定理求出第三个量:垂径课堂小结1、圆是轴对称图形,其对称轴是每一条直径所在的直线或
经过圆心的每一条直线。4、在⊙ O中,若⊙ O的半径r、圆心到弦的距离d、弦长a中,
任意知道两个量,可根据垂径定理求出第三个量:3、 5.2.3定理同学们再见
37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?问题探究用纸剪一个圆,沿着圆的任意
一条直径对折,重复做几次,
你发现了什么?由此你得到了
什么
结论? 圆是轴对称图形,任何一条直
径所在直线都是它的对称轴。结论:如图,AB是圆O的一条弦,作直径CD,
使CD⊥AB,垂足为E.(1)此图是轴对称图
形吗?如果是,它
的对称轴是什么?(2)你能发现图中有哪
些相等的线段和弧?为什么?已知:在⊙o中,CD是直径,AB是弦,CD⊥AB,垂足为E证明:连结OA,OB则OA=OB∵垂直于弦的直径CD所在的直线
既是等腰△OAB的对称轴,
又是⊙O的对称轴∴当把圆沿着直径CD折叠时,
CD两侧的两个半圆重合还有其它方法吗?垂径定理:垂直于弦的直径平分这条弦,
并平分这条弦所对的两条弧问题:此定理的条件和结论分别是什么?推论:1.平分弦(不是直径)的直径垂直于
弦,并且平分弦所对的两条弧。
2.平分弧的直径垂直平分这条弧所对的弦推广:(1)过圆心的直线
(2)垂直弦 (3)平分弦
(4)平分优弧
(5)平分劣弧
由其中两个条件可推出
另外三个结论。5.2.3定理小试牛刀例1:如图,已知在圆O中,弦AB的长为8㎝,
圆心O到AB的距离为3 ㎝,求圆O的半径。现在我们
来解释桥
的问题吧答:赵州桥主桥半径约为27.9m.驶向胜利的彼岸挑战自我1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦.( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行. ( )
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )√???√ 2.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?证明:相等。理由:
过O作OE⊥AB,垂足为E,
∴AE=BE,CE=DE。
∴ AE-CE=BE-DE
∴AC=BD注意:解决有关弦的问题,过圆心作弦的垂线,是一种常用的辅助线添法.CDABE.平分已知弧AB已知:AB
作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:AB的中点⌒⌒你能破镜重圆吗?ABACmn·O 1.作弦AB.AC及它们的垂直平分线m.n,交于O点; 2.以O为圆心,OA为半径作圆。你能破镜重圆吗?ABACmn·O 1.作弦AB.AC及它们的垂直平分线m.n,交于O点; 2.以O为圆心,OA为半径作圆。练习1:在半径为50㎜的圆O中,有长50㎜的
弦AB,计算:
⑴点O与AB的距离;
⑵∠AOB的度数。练习2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。垂径定理的应用 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度. 反思:在⊙ O中,若⊙ O的半径r、
圆心到弦的距离d、弦长a中,
任意知道两个量,可根据 定理求出第三个量:垂径课堂小结1、圆是轴对称图形,其对称轴是每一条直径所在的直线或
经过圆心的每一条直线。4、在⊙ O中,若⊙ O的半径r、圆心到弦的距离d、弦长a中,
任意知道两个量,可根据垂径定理求出第三个量:3、 5.2.3定理同学们再见
