第四章 图形的相似 单元训练(含答案)2024—2025学年北师大版数学九年级上册
文档属性
| 名称 | 第四章 图形的相似 单元训练(含答案)2024—2025学年北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 21:26:45 | ||
图片预览


文档简介
第四章 图形的相似(单元训练)2024—2025学年北师大版数学九年级上册
一、单选题
1.在△ABC中,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB,若BD=2AD,则 的值为( )
A. B. C. D.
2.如图,在的正方形网格中,以O为位似中心,把格点放大为原来的2倍,则A的对应点为( )
A.点 B.点 C.点 D.点
3.如图,直线,分别交直线m、n于点A、C、E、B、D、F,下列结论正确的是( )
A. B. C. D.
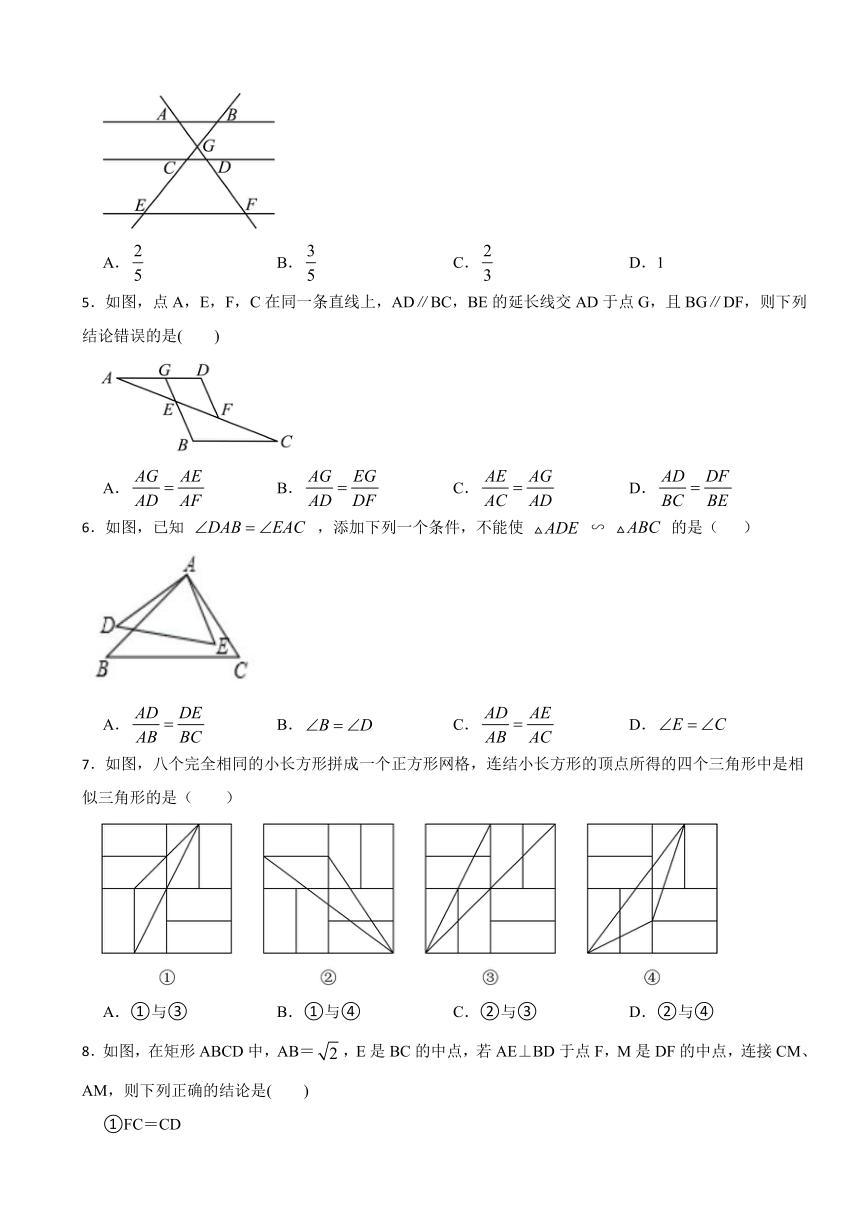
4.如图,,AF与BE交于点G,若,,,则的值为( )
A. B. C. D.1
5.如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
A. B. C. D.
6.如图,已知 ,添加下列一个条件,不能使 ∽ 的是( )
A. B. C. D.
7.如图,八个完全相同的小长方形拼成一个正方形网格,连结小长方形的顶点所得的四个三角形中是相似三角形的是( )
A.①与③ B.①与④ C.②与③ D.②与④
8.如图,在矩形ABCD中,AB=,E是BC的中点,若AE⊥BD于点F,M是DF的中点,连接CM、AM,则下列正确的结论是( )
①FC=CD
②∠DBC=∠FAM
③EF=CM
④矩形ABCD的面积是2
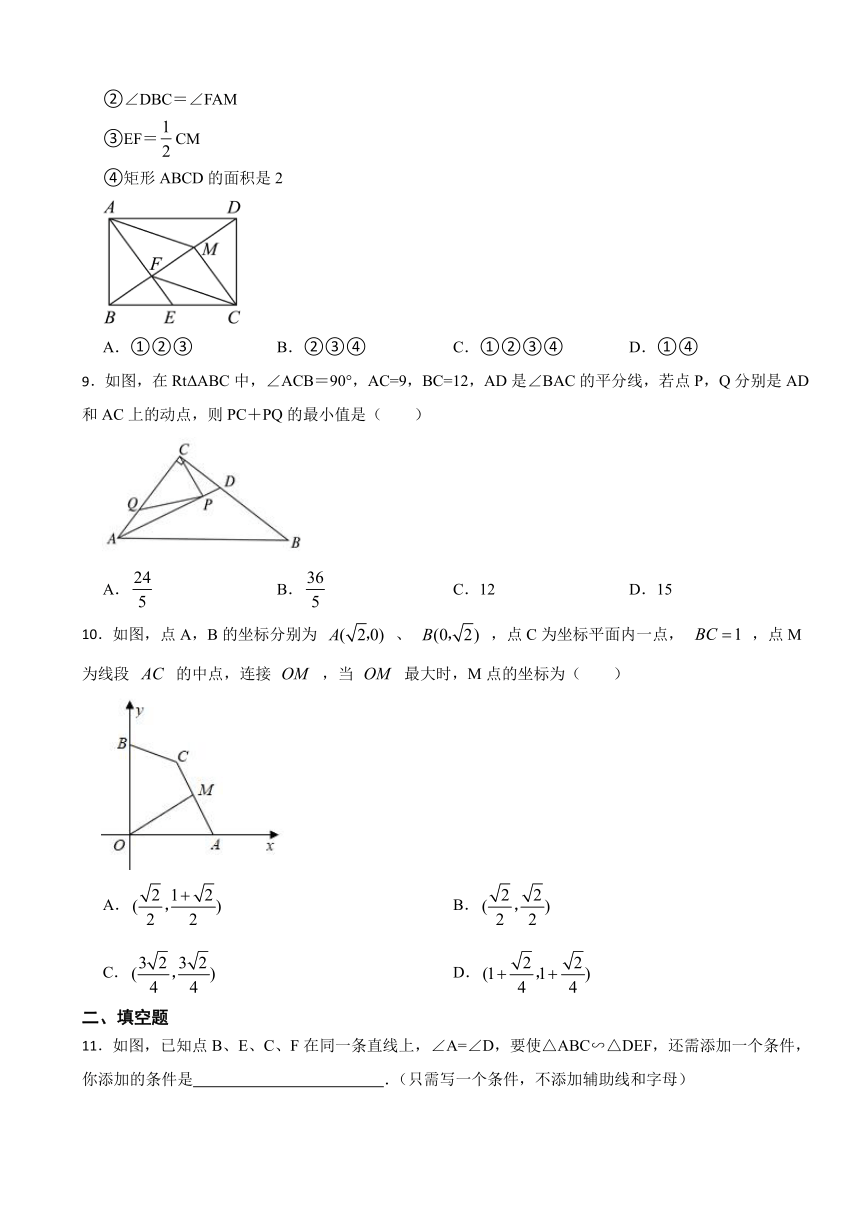
A.①②③ B.②③④ C.①②③④ D.①④
9.如图,在RtΔABC中,∠ACB=90°,AC=9,BC=12,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A. B. C.12 D.15
10.如图,点A,B的坐标分别为 、 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,当 最大时,M点的坐标为( )
A. B.
C. D.
二、填空题
11.如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
12.若线段a,b,c,d成比例线段,且a=1cm,b=2cm,c=3cm,则d的长度是 cm.
13.如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高
14.已知:如图,在中,点在边上,点在边上,要使∽,则需要增加的一个条件是 写出一个即可
15.如图,在中,,点为中点,点在边上,,将沿折叠至,若,则 .
16.如图,在四边形中,,,,若点M,点N分别在边和边上运动,且,连接,则的最小值为 .
17.已知a、b、c、满足 ,从下列四点:① ;②(2,1);③ ;④(1,﹣1),中任意取一点恰好在正比例函数y=kx图象上的概率是 .
三、解答题
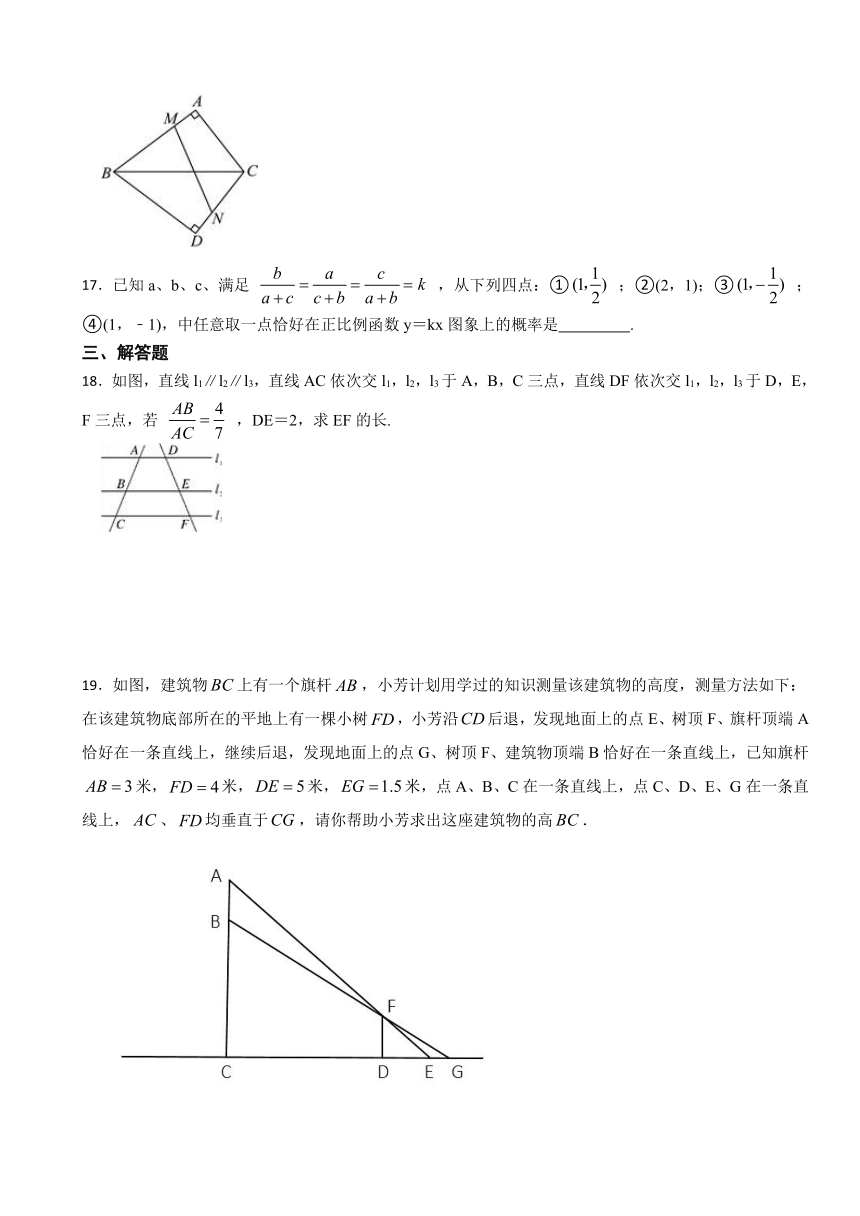
18.如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于A,B,C三点,直线DF依次交l1,l2,l3于D,E,F三点,若 ,DE=2,求EF的长.
19.如图,建筑物上有一个旗杆,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树,小芳沿后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上,已知旗杆米,米,米,米,点A、B、C在一条直线上,点C、D、E、G在一条直线上,、均垂直于,请你帮助小芳求出这座建筑物的高.
20.已知a:b:c=3:4:5.
(1)求代数式的值.
(2)若a-b+c=24,求a,b,c的值.
21.为了测得图甲和图乙中旗杆的高度,小明和小红在查阅资料后,得到一种测量旗杆高度的方法:找到旗杆的影子并找出其顶部,并在影子中间某处放置一竹竿,使得竹竿顶部的影子和旗杆顶部的影子重合,此时竹竿长度和竹竿影长之比即旗杆长度和旗杆影长之比.在太阳光下同一时刻小明和小红分别做了以上操作,测得竹竿CD长0.9m,其影长CE为1m.
(1)如图甲所示,若小明测得旗杆影长AE为3m,求图甲中旗杆高AB为多少米.(CD⊥AE,AB⊥AE,点B,D,E在一条直线上)
(2)如图乙所示,若小红测得旗杆落在地面上的影长FG为3m,落在墙上的影子GH的高为1.1m,则直接写出图乙中旗杆高FP为 m.()
22.如图,在中,、为边上的两个动点,.
(1)若,,则与相似吗?为什么?
(2)若即、重合,则 时,∽;
(3)当和满足怎样的数量关系时,∽?请说明理由.
23.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】∠B=∠DEC(不唯一)
12.【答案】6
13.【答案】8m
14.【答案】(或 )
15.【答案】
16.【答案】
17.【答案】
18.【答案】解:∵l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,
∴ ,
∵ ,DE=2,
∴ ,
解得:DF=3.5,
∴EF=DF-DE=3.5-2=1.5
19.【答案】这座建筑物的高BC为14米.
20.【答案】解: ∵a:b:c=3:4:5,
∴可设a=3k,b=4k,c=5k,
(1) ,
(2) a-b+c=3k-4k+5k=24,
解得:k=6,
∴a=18,b=24,c=30.
21.【答案】(1)解:∵ 竹竿长度和竹竿影长之比即旗杆长度和旗杆影长之比 ,
∴,
即,
∴AB=2.7米;
(2)3.8
22.【答案】(1)解:结论:∽.
理由:,
,
,
,,
,
∽;
(2)90
(3)解:结论:.
理由:,
,
,
当时,则有∽,
,
,
,
在中,,
,
即.
23.【答案】解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M,
∵∠ABG=150°,BE⊥CB,
∴∠MBF=150°﹣90°=60°,
∴∠MFB=30°,
∵BF的长为2米,
∴BM=1米,MF= 米.
∵BE⊥CB,MF⊥BE,
∴BH∥MF,
∴△EBH∽△EMF,
∴ = .
又∵EB=1.8米,
∴ = ,
∴BH= .
∵BE∥CD,
∴△HBE∽△HCD,
∴ = .
∵CB=5 ,
∴ = ,
∴CD=15.8米.
∴大树CD的高度为15.8米.
一、单选题
1.在△ABC中,点D,E,F分别在AB,BC,AC上,且DE∥AC,EF∥AB,若BD=2AD,则 的值为( )
A. B. C. D.
2.如图,在的正方形网格中,以O为位似中心,把格点放大为原来的2倍,则A的对应点为( )
A.点 B.点 C.点 D.点
3.如图,直线,分别交直线m、n于点A、C、E、B、D、F,下列结论正确的是( )
A. B. C. D.
4.如图,,AF与BE交于点G,若,,,则的值为( )
A. B. C. D.1
5.如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
A. B. C. D.
6.如图,已知 ,添加下列一个条件,不能使 ∽ 的是( )
A. B. C. D.
7.如图,八个完全相同的小长方形拼成一个正方形网格,连结小长方形的顶点所得的四个三角形中是相似三角形的是( )
A.①与③ B.①与④ C.②与③ D.②与④
8.如图,在矩形ABCD中,AB=,E是BC的中点,若AE⊥BD于点F,M是DF的中点,连接CM、AM,则下列正确的结论是( )
①FC=CD
②∠DBC=∠FAM
③EF=CM
④矩形ABCD的面积是2
A.①②③ B.②③④ C.①②③④ D.①④
9.如图,在RtΔABC中,∠ACB=90°,AC=9,BC=12,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A. B. C.12 D.15
10.如图,点A,B的坐标分别为 、 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,当 最大时,M点的坐标为( )
A. B.
C. D.
二、填空题
11.如图,已知点B、E、C、F在同一条直线上,∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
12.若线段a,b,c,d成比例线段,且a=1cm,b=2cm,c=3cm,则d的长度是 cm.
13.如图,铁道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高
14.已知:如图,在中,点在边上,点在边上,要使∽,则需要增加的一个条件是 写出一个即可
15.如图,在中,,点为中点,点在边上,,将沿折叠至,若,则 .
16.如图,在四边形中,,,,若点M,点N分别在边和边上运动,且,连接,则的最小值为 .
17.已知a、b、c、满足 ,从下列四点:① ;②(2,1);③ ;④(1,﹣1),中任意取一点恰好在正比例函数y=kx图象上的概率是 .
三、解答题
18.如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于A,B,C三点,直线DF依次交l1,l2,l3于D,E,F三点,若 ,DE=2,求EF的长.
19.如图,建筑物上有一个旗杆,小芳计划用学过的知识测量该建筑物的高度,测量方法如下:在该建筑物底部所在的平地上有一棵小树,小芳沿后退,发现地面上的点E、树顶F、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶F、建筑物顶端B恰好在一条直线上,已知旗杆米,米,米,米,点A、B、C在一条直线上,点C、D、E、G在一条直线上,、均垂直于,请你帮助小芳求出这座建筑物的高.
20.已知a:b:c=3:4:5.
(1)求代数式的值.
(2)若a-b+c=24,求a,b,c的值.
21.为了测得图甲和图乙中旗杆的高度,小明和小红在查阅资料后,得到一种测量旗杆高度的方法:找到旗杆的影子并找出其顶部,并在影子中间某处放置一竹竿,使得竹竿顶部的影子和旗杆顶部的影子重合,此时竹竿长度和竹竿影长之比即旗杆长度和旗杆影长之比.在太阳光下同一时刻小明和小红分别做了以上操作,测得竹竿CD长0.9m,其影长CE为1m.
(1)如图甲所示,若小明测得旗杆影长AE为3m,求图甲中旗杆高AB为多少米.(CD⊥AE,AB⊥AE,点B,D,E在一条直线上)
(2)如图乙所示,若小红测得旗杆落在地面上的影长FG为3m,落在墙上的影子GH的高为1.1m,则直接写出图乙中旗杆高FP为 m.()
22.如图,在中,、为边上的两个动点,.
(1)若,,则与相似吗?为什么?
(2)若即、重合,则 时,∽;
(3)当和满足怎样的数量关系时,∽?请说明理由.
23.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】∠B=∠DEC(不唯一)
12.【答案】6
13.【答案】8m
14.【答案】(或 )
15.【答案】
16.【答案】
17.【答案】
18.【答案】解:∵l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,
∴ ,
∵ ,DE=2,
∴ ,
解得:DF=3.5,
∴EF=DF-DE=3.5-2=1.5
19.【答案】这座建筑物的高BC为14米.
20.【答案】解: ∵a:b:c=3:4:5,
∴可设a=3k,b=4k,c=5k,
(1) ,
(2) a-b+c=3k-4k+5k=24,
解得:k=6,
∴a=18,b=24,c=30.
21.【答案】(1)解:∵ 竹竿长度和竹竿影长之比即旗杆长度和旗杆影长之比 ,
∴,
即,
∴AB=2.7米;
(2)3.8
22.【答案】(1)解:结论:∽.
理由:,
,
,
,,
,
∽;
(2)90
(3)解:结论:.
理由:,
,
,
当时,则有∽,
,
,
,
在中,,
,
即.
23.【答案】解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M,
∵∠ABG=150°,BE⊥CB,
∴∠MBF=150°﹣90°=60°,
∴∠MFB=30°,
∵BF的长为2米,
∴BM=1米,MF= 米.
∵BE⊥CB,MF⊥BE,
∴BH∥MF,
∴△EBH∽△EMF,
∴ = .
又∵EB=1.8米,
∴ = ,
∴BH= .
∵BE∥CD,
∴△HBE∽△HCD,
∴ = .
∵CB=5 ,
∴ = ,
∴CD=15.8米.
∴大树CD的高度为15.8米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
