数学:2.3二次函数y=ax^2的图象和性质课件(鲁教版九年级上)
文档属性
| 名称 | 数学:2.3二次函数y=ax^2的图象和性质课件(鲁教版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 178.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-22 00:00:00 | ||
图片预览


文档简介
课件10张PPT。2.3二次函数y=ax2的图象和性质引入学习了正比例函数,一次函数与反比例函数的定义后,研究了它们各自的图象特征,下面请同学们谈谈它们的图象有拿些特征?
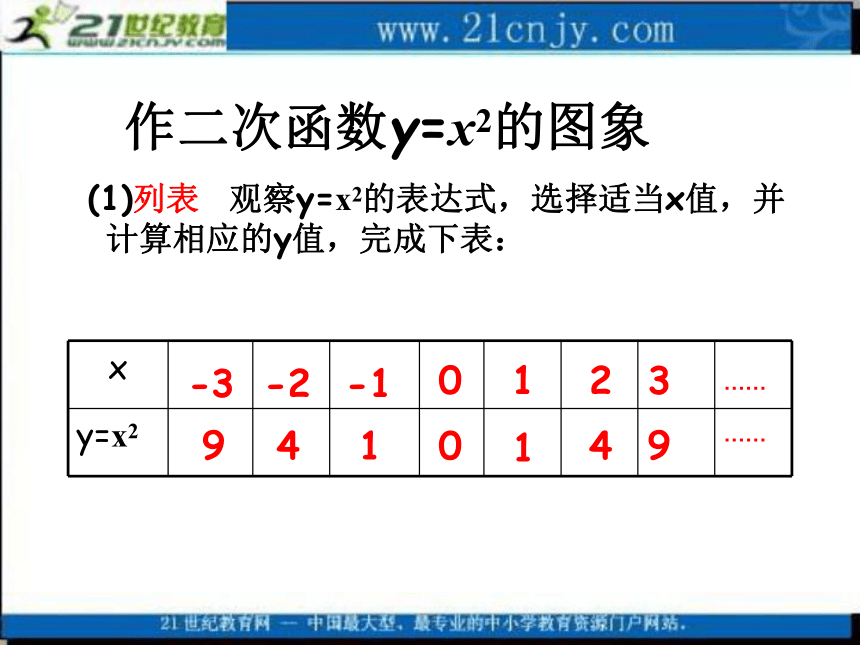
上节课我们学习了二次函数的一般形式为y=ax2+bx+c(a ≠ 0),那么它的图象是否也为直线或为双曲线呢?作二次函数y=x2的图象 (1)列表 观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
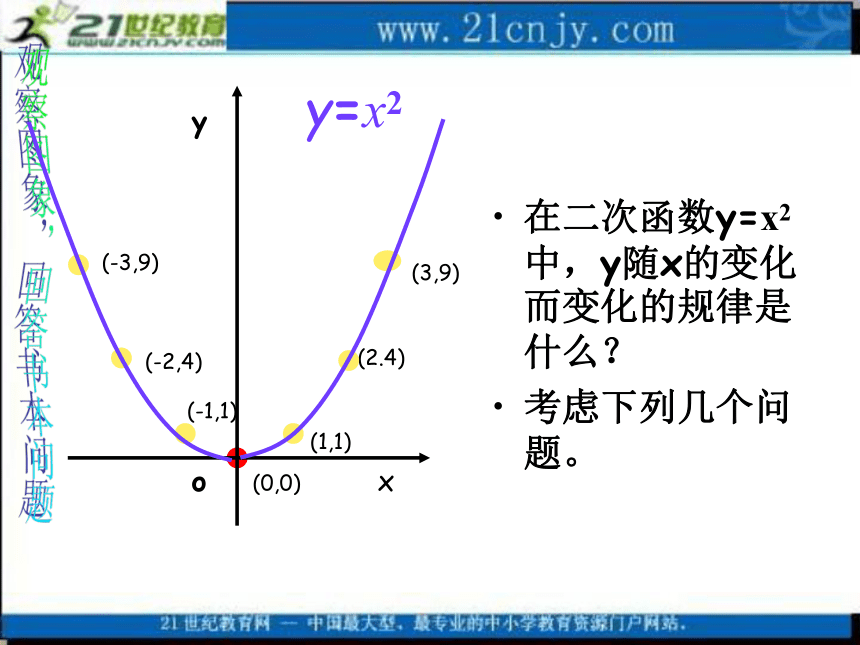
(-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)观察图象,回答书本问题yxy=x2o(0,0)在二次函数y=x2中,y随x的变化而变化的规律是什么?
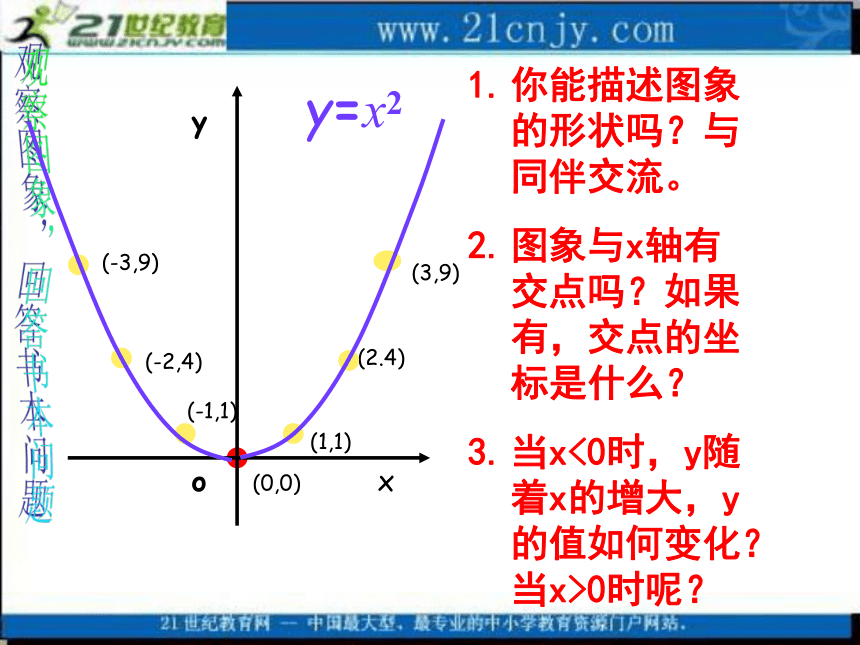
考虑下列几个问题。(-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)观察图象,回答书本问题yxy=x2o(0,0)你能描述图象的形状吗?与同伴交流。
图象与x轴有交点吗?如果有,交点的坐标是什么?
当x<0时,y随着x的增大,y的值如何变化?当x>0时呢?(-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)观察图象,回答书本问题yxy=x2o(0,0)4、当x取什么值时,y的值最小?
5、图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流。归纳:二次函数y=x2的图象是一条抛物线,它的开口向上,且关于y轴对称,对称轴与抛物线的交点是抛物线的顶点,它是图象的最底点。做一做
二次函数y=-x2的图象是什么形状?
先想一想,然后作出它的图象.
它与二次函数y=x2的图象有什么关系?y=x2y=-x2yxo练习:1.在同一直角坐标系中画出函数y=x2与y=-x2的图象。yxxy=x2y=-x2yoo相同点:图象都是抛物线;图象都与x轴脚与点 (0,0);图象都关于y轴对称。
不同点:开口方向不同;函数值随自变量增大的变化趋势不同;最值不同;一个有最高点,一个有最低点。
联系:它们的图象关于x轴对称。
活动与探索已知二次函数y=mxm2+m当m取何值时它的图象开口向上。 (1)当x取何值时y随x的增大而增大。(2)当x取何值时y随x的增大而减小。
当m取何值时它的图象开口向下。 (1)当x取何值时y随x的增大而增大。(2)当x取何值时y随x的增大而减小。
上节课我们学习了二次函数的一般形式为y=ax2+bx+c(a ≠ 0),那么它的图象是否也为直线或为双曲线呢?作二次函数y=x2的图象 (1)列表 观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
(-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)观察图象,回答书本问题yxy=x2o(0,0)在二次函数y=x2中,y随x的变化而变化的规律是什么?
考虑下列几个问题。(-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)观察图象,回答书本问题yxy=x2o(0,0)你能描述图象的形状吗?与同伴交流。
图象与x轴有交点吗?如果有,交点的坐标是什么?
当x<0时,y随着x的增大,y的值如何变化?当x>0时呢?(-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)观察图象,回答书本问题yxy=x2o(0,0)4、当x取什么值时,y的值最小?
5、图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流。归纳:二次函数y=x2的图象是一条抛物线,它的开口向上,且关于y轴对称,对称轴与抛物线的交点是抛物线的顶点,它是图象的最底点。做一做
二次函数y=-x2的图象是什么形状?
先想一想,然后作出它的图象.
它与二次函数y=x2的图象有什么关系?y=x2y=-x2yxo练习:1.在同一直角坐标系中画出函数y=x2与y=-x2的图象。yxxy=x2y=-x2yoo相同点:图象都是抛物线;图象都与x轴脚与点 (0,0);图象都关于y轴对称。
不同点:开口方向不同;函数值随自变量增大的变化趋势不同;最值不同;一个有最高点,一个有最低点。
联系:它们的图象关于x轴对称。
活动与探索已知二次函数y=mxm2+m当m取何值时它的图象开口向上。 (1)当x取何值时y随x的增大而增大。(2)当x取何值时y随x的增大而减小。
当m取何值时它的图象开口向下。 (1)当x取何值时y随x的增大而增大。(2)当x取何值时y随x的增大而减小。
