北师大版数学六年级下册第一单元圆柱与圆锥的体积(课件)(共17张PPT)
文档属性
| 名称 | 北师大版数学六年级下册第一单元圆柱与圆锥的体积(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 952.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 09:35:59 | ||
图片预览



文档简介
(共17张PPT)
圆柱与圆锥的体积
(复习与整理)
看看谁的反应快
6.5L=( )mL 4500mL =( )L( )ml
2300dm3=( )m3 0.083m3=( )dm3
复习目标
1. 进一步掌握圆柱与圆锥的体积计算方法。
2. 明确圆柱与圆锥的体积关系。
3. 运用圆柱与圆锥的体积知识解决常见的
生活问题。
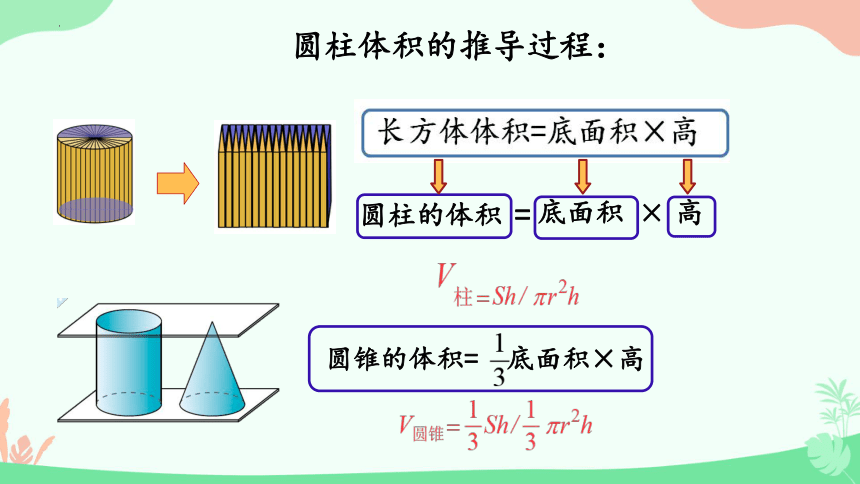
圆柱体积的推导过程:
圆锥的体积= 底面积×高
圆柱的体积
底面积
高
=
×
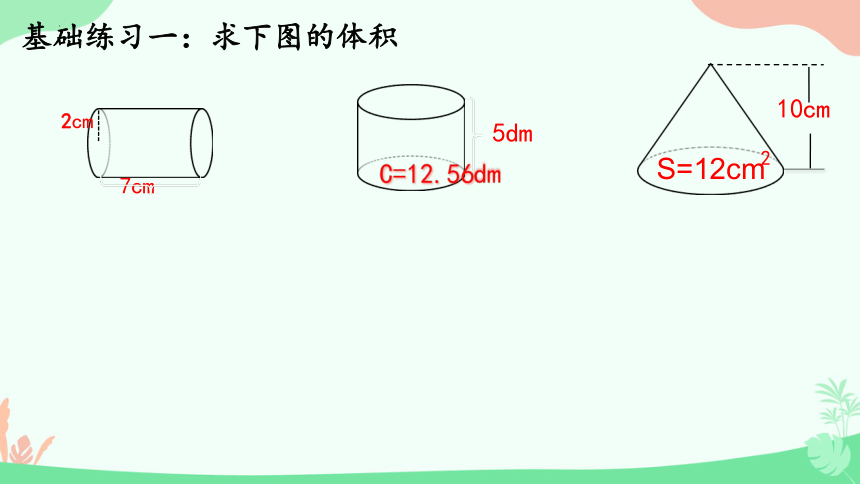
基础练习一:求下图的体积
5dm
2cm
7cm
10cm
S=12cm
C=12.56dm
2
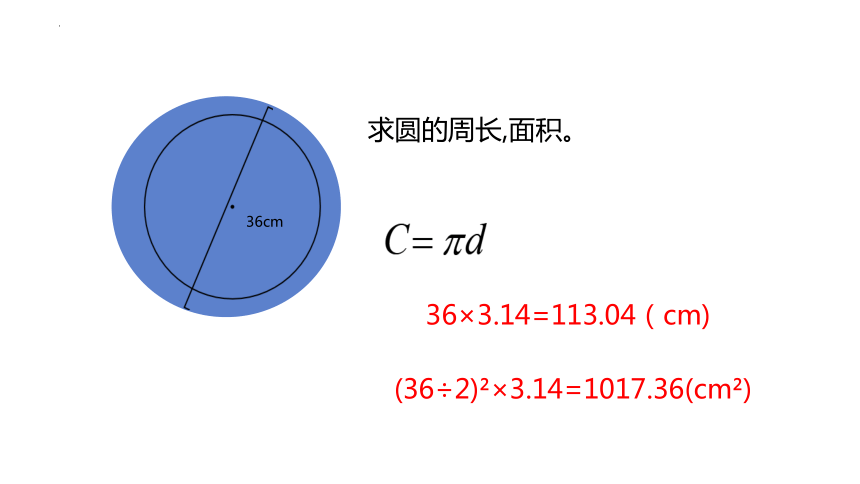
36cm
求圆的周长,面积。
(36÷2) ×3.14=1017.36(cm )
36×3.14=113.04(cm)
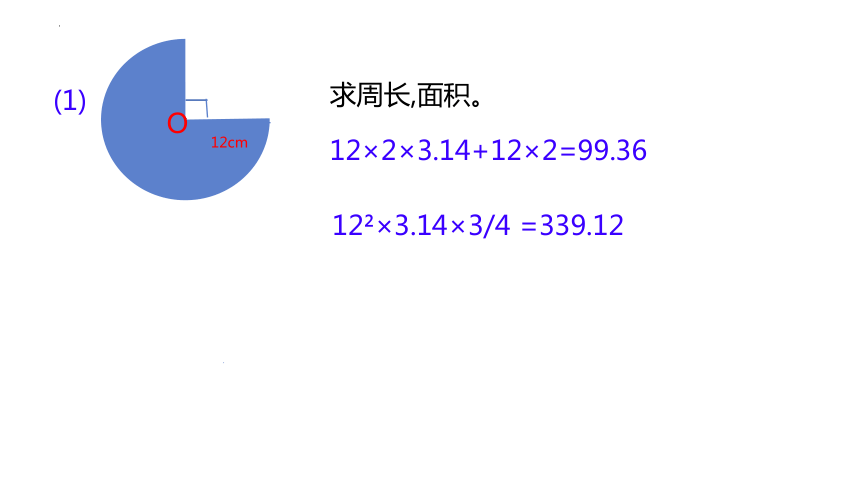
O
12cm
求周长,面积。
12 ×3.14×3/4 =339.12
12×2×3.14+12×2=99.36
(1)
练习应用
试试看
判断:
解决问题
一一个圆锥形的沙堆, 底面周长是12.56米, 高3米,如果每立方米沙重3吨,这堆沙约重多少吨?形的稻谷堆, 底周长12.56米, 高1.5米,
提升练习:求铁块的体积
10cm
4cm
10cm
7cm
提示:液体升高部分的体积等于铁块的体积。
拓展延伸
用不同的方法表述等底等高的圆柱与圆锥的体积关系
4.把一块长6厘米,宽4厘米,高5厘米的铁块熔铸成一个高10厘米的圆锥,这个圆锥的底面积是多少平方厘米?
提示:熔铸问题,熔铸前后体积不变。
拓展延伸
下节课见!
圆柱与圆锥的体积
(复习与整理)
看看谁的反应快
6.5L=( )mL 4500mL =( )L( )ml
2300dm3=( )m3 0.083m3=( )dm3
复习目标
1. 进一步掌握圆柱与圆锥的体积计算方法。
2. 明确圆柱与圆锥的体积关系。
3. 运用圆柱与圆锥的体积知识解决常见的
生活问题。
圆柱体积的推导过程:
圆锥的体积= 底面积×高
圆柱的体积
底面积
高
=
×
基础练习一:求下图的体积
5dm
2cm
7cm
10cm
S=12cm
C=12.56dm
2
36cm
求圆的周长,面积。
(36÷2) ×3.14=1017.36(cm )
36×3.14=113.04(cm)
O
12cm
求周长,面积。
12 ×3.14×3/4 =339.12
12×2×3.14+12×2=99.36
(1)
练习应用
试试看
判断:
解决问题
一一个圆锥形的沙堆, 底面周长是12.56米, 高3米,如果每立方米沙重3吨,这堆沙约重多少吨?形的稻谷堆, 底周长12.56米, 高1.5米,
提升练习:求铁块的体积
10cm
4cm
10cm
7cm
提示:液体升高部分的体积等于铁块的体积。
拓展延伸
用不同的方法表述等底等高的圆柱与圆锥的体积关系
4.把一块长6厘米,宽4厘米,高5厘米的铁块熔铸成一个高10厘米的圆锥,这个圆锥的底面积是多少平方厘米?
提示:熔铸问题,熔铸前后体积不变。
拓展延伸
下节课见!
