13.3.2等边三角形(2) 课件(共19张PPT)
文档属性
| 名称 | 13.3.2等边三角形(2) 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 19:48:03 | ||
图片预览





文档简介
(共19张PPT)
人教版 八年级数学上
13.3.2等边三角形(2)
学习目标
1.探索含30°角的直角三角形的性质.(重点)
2.能灵活运用含30°角的直角三角形进行有关推理证明.
(难点)
合作探究
思考1:如图,将两个相同的含30°角的三角尺摆放在一起,你能
借助这个图形,得到原直角三角形中短的直角边与斜边之
间的数量关系吗?
分离
拼接
你能证明
这个结论吗?
短的直角边等于斜边的一半.
合作探究
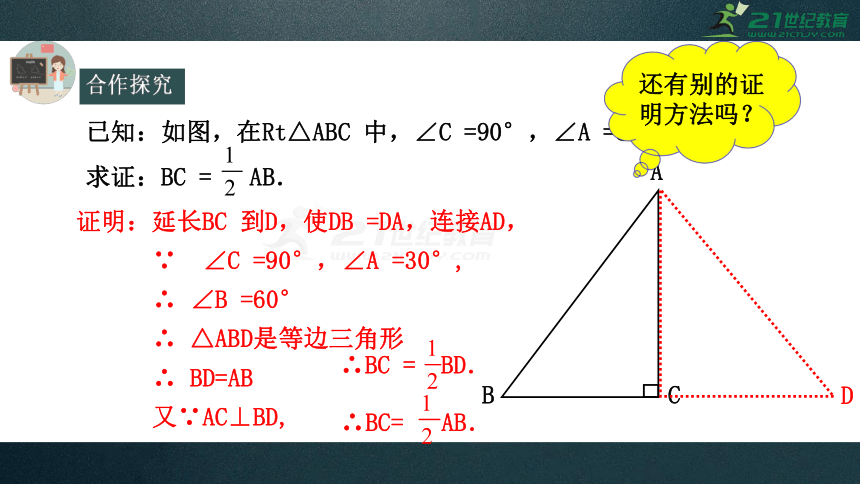
证明:延长BC 到D,使DB =DA,连接AD,
∵ ∠C =90°,∠A =30°,
∴ ∠B =60°
∴ △ABD是等边三角形
∴ BD=AB
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
求证:BC = AB.
A
B
C
D
∴BC= AB.
∴BC = BD.
还有别的证
明方法吗?
合作探究
E
A
B
C
证明2: 在BA上截取BE=BC,连接EC.
∵ ∠B= 60° ,BE=BC.
∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC-∠A=60°-30°=30°.
∴ AE=EC, ∴ AE=BE=BC,
∴ AB=AE+BE=2BC.
∴ BC = AB.
合作探究
A
B
C
归纳总结:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
符号语言:∵∠C =90°, ∠A=30°
∴ BC = AB.
典例精析
例.如图是屋架设计图的一部分,点D 是斜梁AB的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC、DE 要多长?
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,DE = AD.
又 AD = AB,
∴DE = AD =1.85(m) .
∴ BC =3.7(m).
答:立柱BC 的长是3.7 m,DE 的长是1.85 m.
小试牛刀
1.如图,一棵树在一次强台风中于离地面8米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.8米 B.12米 C.16米 D.24米
D
2.在△ABC中,∠B=90° AB=6,∠C=30°,点Q是BC上的一个动点,连接AQ,那么AQ的长度不可能是( )
A.7 B.8.5 C.13 D.12
C
B
Q
A
C
小试牛刀
3.在Rt△ABC中,∠C=90°,∠B=2∠A, 则∠B= ,∠A = ,边AB与BC之间的关系是 。
60°
4.如图,两条铁道路线AC与AD相交于车站A,B市在∠CAD的角平分线上,且距车站A的距离为30km,∠DAC=60°,则B市与铁路AD路线的距离为______km.
30°
AB=2BC
A
C
D
B
15
小试牛刀
5.如图,∠ACB=90°,CD是高,∠A=30°,求证:BD= AB.
证明: ∵∠ACB=90°,∠A=30°,
∴BC= AB,∠B=60°
∵CD是高,
∴∠CDB=90°,∠B=60°,
∴∠BCD=30°,
∴BD= BC, ∴BD= AB.
课堂小结
今天我们收获了哪些知识?(畅所欲言)
1、含30°角的直角三角形的性质是什么?
2、需要注意什么?
实战演练
E
A
1.如图,OP平分∠AOB,∠AOP=15°,PC∥OA交OB于C,PD⊥OA于D,若PC=6,则PD等于( )
A.3 B.5
C. 6 D.4
2.等腰三角形的底角是15°,腰长18,则其腰上的高为( )
A.9 B.5
C. 6 D.8
A
实战演练
3.含30°角的直角三角板与直线a,b的位置关系如图所示,已知a∥b,∠A=30°, ∠1=60° 若AB=8,则CD的长为=____.
4
A
B
C
D
a
b
1
4.如图,在△ABC中,AB=AC,∠BAC=120°, AD⊥AC交BC于点D,AD=6,则BC=____.
A
B
C
D
18
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=5,求BC的长
解:(1)∵∠C=90°.
∴∠CAB+ ∠B=90°
∵AD是∠CAB的平分线,
∴∠1=∠2.
1
2
A
B
C
D
E
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=5,求BC的长
又∵ DE⊥AB ,
∴∠DEA=∠DEB=90°
∵点E为AB的中点
∴AE=BE
∵DE=DE ∴△AED≌△BED(ASA),
1
2
A
B
C
D
E
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=5,求BC的长
∴∠2=∠B
∴∠1=∠2=∠B
∴∠1+ ∠2+∠B=90°
∴∠B=30°
1
2
A
B
C
D
E
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=6,求BC的长
(2)由(1)知:∠1=∠2=∠B=30°
∴ Rt△BDE中, DB=2DE=12
∵ AD是∠BAC的平分线, DE⊥AB, DC⊥AC
∴DC=DE=6
∴BD=DC+DB=18.
1
2
A
B
C
D
E
课后作业
教材83页习题13.3第14、15题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
13.3.2等边三角形(2)
学习目标
1.探索含30°角的直角三角形的性质.(重点)
2.能灵活运用含30°角的直角三角形进行有关推理证明.
(难点)
合作探究
思考1:如图,将两个相同的含30°角的三角尺摆放在一起,你能
借助这个图形,得到原直角三角形中短的直角边与斜边之
间的数量关系吗?
分离
拼接
你能证明
这个结论吗?
短的直角边等于斜边的一半.
合作探究
证明:延长BC 到D,使DB =DA,连接AD,
∵ ∠C =90°,∠A =30°,
∴ ∠B =60°
∴ △ABD是等边三角形
∴ BD=AB
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
求证:BC = AB.
A
B
C
D
∴BC= AB.
∴BC = BD.
还有别的证
明方法吗?
合作探究
E
A
B
C
证明2: 在BA上截取BE=BC,连接EC.
∵ ∠B= 60° ,BE=BC.
∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC-∠A=60°-30°=30°.
∴ AE=EC, ∴ AE=BE=BC,
∴ AB=AE+BE=2BC.
∴ BC = AB.
合作探究
A
B
C
归纳总结:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
符号语言:∵∠C =90°, ∠A=30°
∴ BC = AB.
典例精析
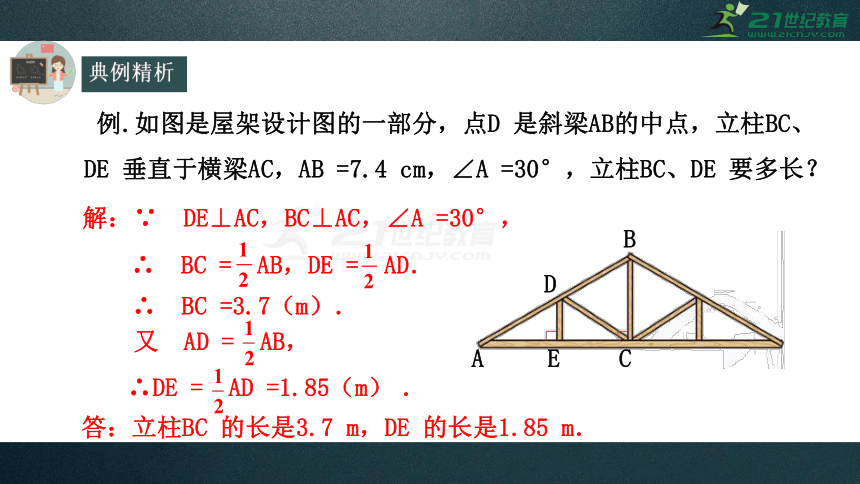
例.如图是屋架设计图的一部分,点D 是斜梁AB的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC、DE 要多长?
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,DE = AD.
又 AD = AB,
∴DE = AD =1.85(m) .
∴ BC =3.7(m).
答:立柱BC 的长是3.7 m,DE 的长是1.85 m.
小试牛刀
1.如图,一棵树在一次强台风中于离地面8米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.8米 B.12米 C.16米 D.24米
D
2.在△ABC中,∠B=90° AB=6,∠C=30°,点Q是BC上的一个动点,连接AQ,那么AQ的长度不可能是( )
A.7 B.8.5 C.13 D.12
C
B
Q
A
C
小试牛刀
3.在Rt△ABC中,∠C=90°,∠B=2∠A, 则∠B= ,∠A = ,边AB与BC之间的关系是 。
60°
4.如图,两条铁道路线AC与AD相交于车站A,B市在∠CAD的角平分线上,且距车站A的距离为30km,∠DAC=60°,则B市与铁路AD路线的距离为______km.
30°
AB=2BC
A
C
D
B
15
小试牛刀
5.如图,∠ACB=90°,CD是高,∠A=30°,求证:BD= AB.
证明: ∵∠ACB=90°,∠A=30°,
∴BC= AB,∠B=60°
∵CD是高,
∴∠CDB=90°,∠B=60°,
∴∠BCD=30°,
∴BD= BC, ∴BD= AB.
课堂小结
今天我们收获了哪些知识?(畅所欲言)
1、含30°角的直角三角形的性质是什么?
2、需要注意什么?
实战演练
E
A
1.如图,OP平分∠AOB,∠AOP=15°,PC∥OA交OB于C,PD⊥OA于D,若PC=6,则PD等于( )
A.3 B.5
C. 6 D.4
2.等腰三角形的底角是15°,腰长18,则其腰上的高为( )
A.9 B.5
C. 6 D.8
A
实战演练
3.含30°角的直角三角板与直线a,b的位置关系如图所示,已知a∥b,∠A=30°, ∠1=60° 若AB=8,则CD的长为=____.
4
A
B
C
D
a
b
1
4.如图,在△ABC中,AB=AC,∠BAC=120°, AD⊥AC交BC于点D,AD=6,则BC=____.
A
B
C
D
18
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=5,求BC的长
解:(1)∵∠C=90°.
∴∠CAB+ ∠B=90°
∵AD是∠CAB的平分线,
∴∠1=∠2.
1
2
A
B
C
D
E
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=5,求BC的长
又∵ DE⊥AB ,
∴∠DEA=∠DEB=90°
∵点E为AB的中点
∴AE=BE
∵DE=DE ∴△AED≌△BED(ASA),
1
2
A
B
C
D
E
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=5,求BC的长
∴∠2=∠B
∴∠1=∠2=∠B
∴∠1+ ∠2+∠B=90°
∴∠B=30°
1
2
A
B
C
D
E
实战演练
5.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB,且点E为AB的中点.
(1)求∠B的度数
(2)若DE=6,求BC的长
(2)由(1)知:∠1=∠2=∠B=30°
∴ Rt△BDE中, DB=2DE=12
∵ AD是∠BAC的平分线, DE⊥AB, DC⊥AC
∴DC=DE=6
∴BD=DC+DB=18.
1
2
A
B
C
D
E
课后作业
教材83页习题13.3第14、15题.
https://www.21cnjy.com/help/help_extract.php
