4.2.2 指数函数的图象和性质 课件(共20张PPT) 2024~2025学年高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.2.2 指数函数的图象和性质 课件(共20张PPT) 2024~2025学年高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 897.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
4.2.2 指数函数的图象和性质
学习目标
1.通过画出具体指数函数的图象,探究指数函数的性质.
情境引入
对折 x 次,厚度y=_____________
假设一张矩形纸张厚度为1
对折 1 次,厚度为
对折 2 次,厚度为
对折 3 次,厚度为
···
新课讲授
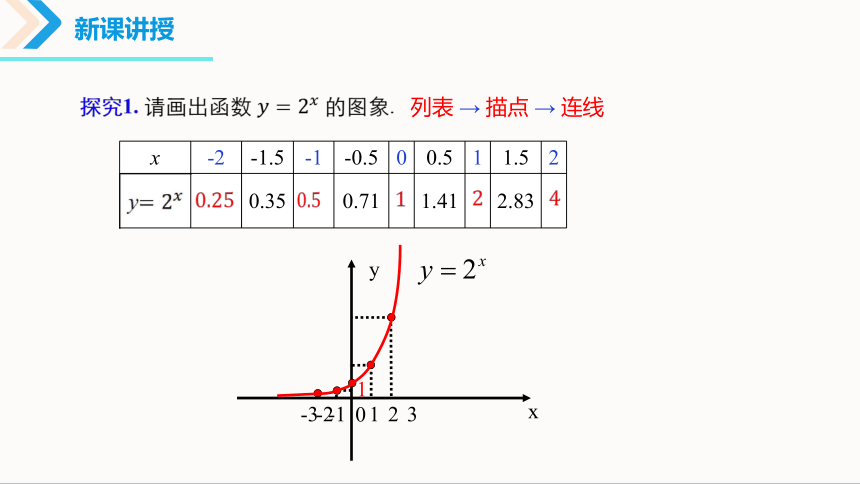
探究1. 请画出函数 的图象.
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y 0.35 0.71 1.41 2.83
列表 → 描点 → 连线
x
y
0
1
2
3
-1
-2
-3
1
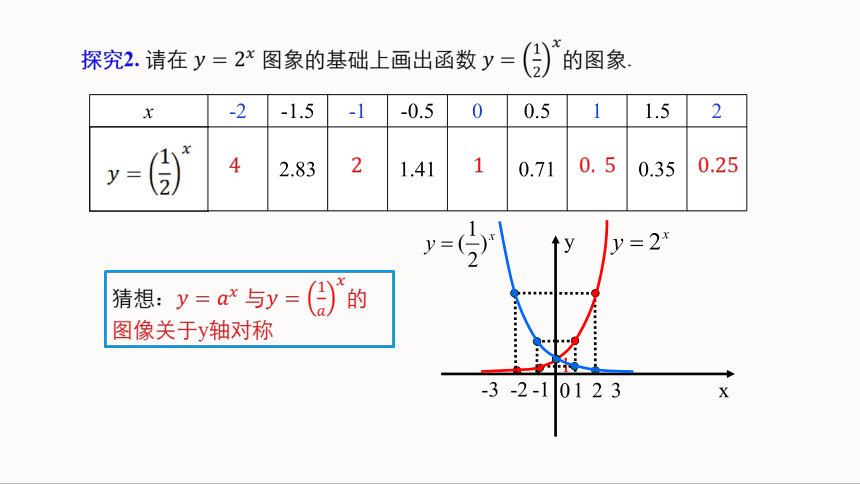
探究2. 请在 图象的基础上画出函数 的图象.
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
2.83 1.41 0.71 0.35
x
y
0
1
2
3
-1
-2
-3
1
猜想 与的图像关于y轴对称
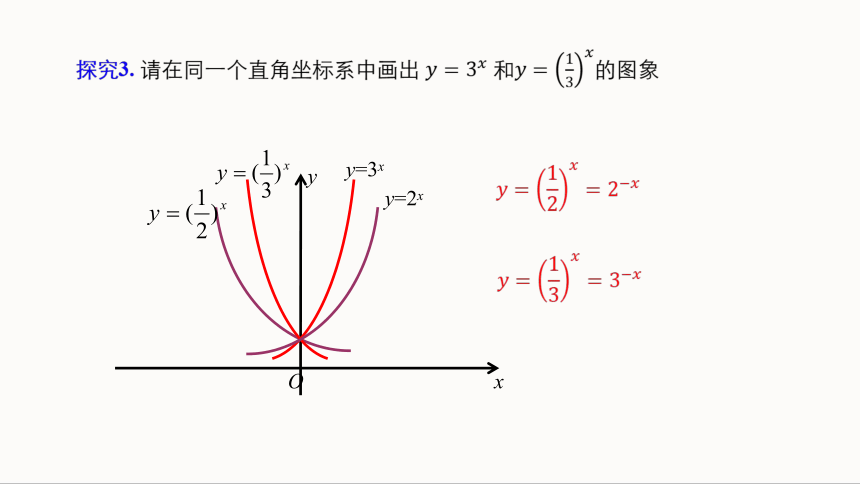
探究3. 请在同一个直角坐标系中画出 和的图象
x
O
y
y=3x
y=2x
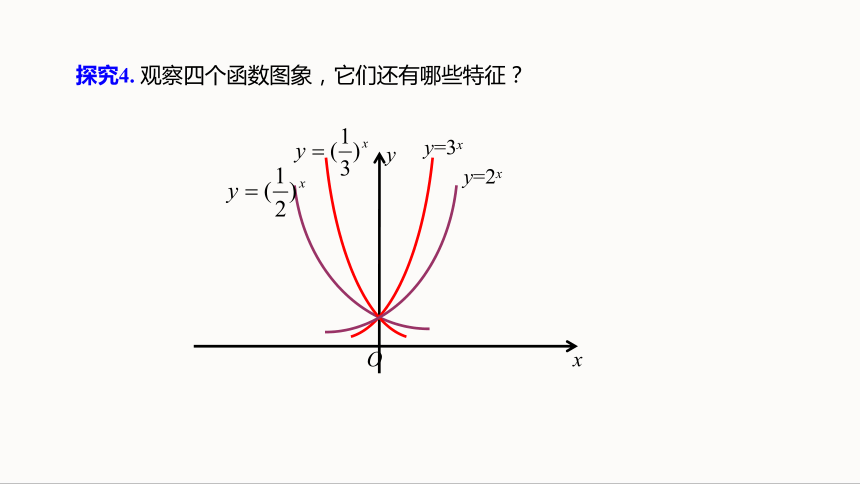
探究4. 观察四个函数图象,它们还有哪些特征?
x
O
y
y=3x
y=2x
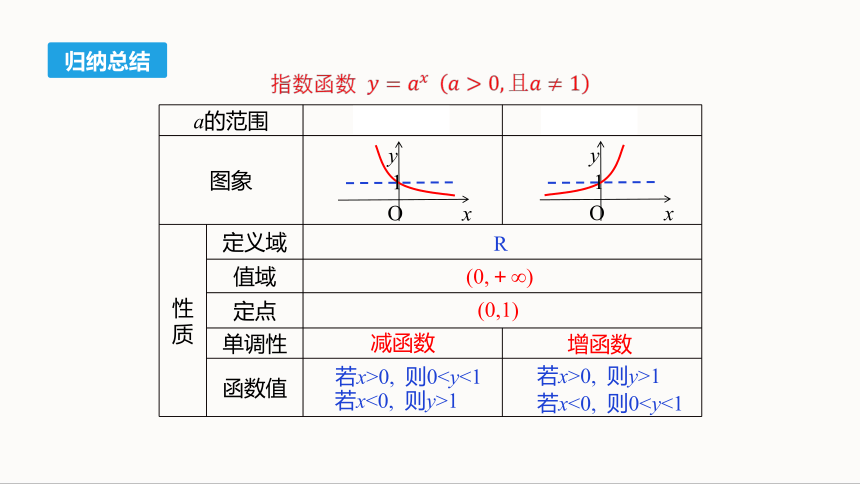
归纳总结
a的范围 01
图象
性质 定义域 值域 定点 单调性
函数值
若x>0, 则y>1
若x<0, 则0若x>0, 则0若x<0, 则y>1
R
(0,+∞)
(0,1)
增函数
减函数
O
x
y
1
O
x
y
1
指数函数
注意
(1)函数图象只出现在x轴上方.
(2)当x=0时,有a0=1,故过定点(0,1).
(3)当0(4)当a>1时,底数越大,图象越靠近y轴.
(5)任意底数互为倒数的两个指数函数的图象关于y轴对称.
例1 如图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.aB.bC.1D.aB
(1)1.72.5 与1.73 (2) 与
例2 利用指数函数的单调性,比较下列各题中两个值的大小.
解 :(1) ∵ 1
∴函数是增函数
又∵ 2.53 ∴ 1.72.51.73
(2)∵ 1
∴函数是减函数
又∵ ∴
同底数幂比大小:
借助指数函数单调性
O
x
y
1
O
x
y
1
练1. 比较 与 的大小关系.
解: ① 当时,
② 当 时,
同底数幂比大小:
底数未知时分类讨论!
练2. 比较 1.70.3 与 0.93.1 的大小关系.
解:∵ 1.70.3 1.70
且 0.93.1 0.90
∴ 1.70.3 0.93.1
不同底数幂(指数不同)
比大小:借助中间值“1”塔桥
指数式比大小
①底数相同(指数不同)
借助指数函数单调性比大小
②底数不同(指数不同)
借助中间值,如与“1”比较大小 (搭桥法)
归纳总结
例3 若函数f(x)=2ax+m-n(a>0,且a≠1)的图象恒过点(-1,4),则m+n等于( )
A.3 B.1 C.-1 D.-2
解析:由函数f(x)=2ax+m-n(a>0,且a≠1)的图象恒过(-1,4),
得m-1=0,2·am-1-n=4,
解得m=1,n=-2,
∴m+n=-1.
C
∴3x-1≥-1,∴x≥0,
故原不等式的解集是{x|x≥0}.
解:
解:设g(x)=x2+2(a-1)x+2,指数函数h(x)=在R上单调递减,
根据复合函数单调性同增异减的原则可知函数g(x)=x2+2(a-1)x+2在区间
(-∞,4]上单调递减.
由于函数g(x)=x2+2(a-1)x+2的图象开口向上,且对称轴为直线x=1-a,
要使函数f(x)在区间(-∞,4]上单调递增,则4≤1-a,即a≤-3.
故a的取值范围为(-∞,-3].
课堂总结
a的范围 01
图象
性质 定义域 值域 定点 单调性
函数值
若x>0, 则y>1
若x<0, 则0若x>0, 则0若x<0, 则y>1
R
(0,+∞)
(0,1)
增函数
减函数
O
x
y
1
O
x
y
1
指数函数
当堂检测
1.函数 y=2-x 的大致图象是( )
B
2.已知指数函数y=(2a-1)x 为减函数,则a的取值范围为_____________.
当堂检测
3. 用“”或“<”填空
(1) 3.10.5 ____ 3.12.3
(2) ____
(3)
(4)2.3-2.5 ____ 0.2-0.1
<
<
<
当堂检测
4. 如果 a-5x > ax+7 (a>0,且a≠1),求x的取值范围.
解 :① 当 时,-5x x+7,则 x
② 当 时, -5xx+7,则 x
综上,当 时,
当 时,
4.2.2 指数函数的图象和性质
学习目标
1.通过画出具体指数函数的图象,探究指数函数的性质.
情境引入
对折 x 次,厚度y=_____________
假设一张矩形纸张厚度为1
对折 1 次,厚度为
对折 2 次,厚度为
对折 3 次,厚度为
···
新课讲授
探究1. 请画出函数 的图象.
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
y 0.35 0.71 1.41 2.83
列表 → 描点 → 连线
x
y
0
1
2
3
-1
-2
-3
1
探究2. 请在 图象的基础上画出函数 的图象.
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
2.83 1.41 0.71 0.35
x
y
0
1
2
3
-1
-2
-3
1
猜想 与的图像关于y轴对称
探究3. 请在同一个直角坐标系中画出 和的图象
x
O
y
y=3x
y=2x
探究4. 观察四个函数图象,它们还有哪些特征?
x
O
y
y=3x
y=2x
归纳总结
a的范围 0
图象
性质 定义域 值域 定点 单调性
函数值
若x>0, 则y>1
若x<0, 则0
R
(0,+∞)
(0,1)
增函数
减函数
O
x
y
1
O
x
y
1
指数函数
注意
(1)函数图象只出现在x轴上方.
(2)当x=0时,有a0=1,故过定点(0,1).
(3)当0
(5)任意底数互为倒数的两个指数函数的图象关于y轴对称.
例1 如图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.a
(1)1.72.5 与1.73 (2) 与
例2 利用指数函数的单调性,比较下列各题中两个值的大小.
解 :(1) ∵ 1
∴函数是增函数
又∵ 2.53 ∴ 1.72.51.73
(2)∵ 1
∴函数是减函数
又∵ ∴
同底数幂比大小:
借助指数函数单调性
O
x
y
1
O
x
y
1
练1. 比较 与 的大小关系.
解: ① 当时,
② 当 时,
同底数幂比大小:
底数未知时分类讨论!
练2. 比较 1.70.3 与 0.93.1 的大小关系.
解:∵ 1.70.3 1.70
且 0.93.1 0.90
∴ 1.70.3 0.93.1
不同底数幂(指数不同)
比大小:借助中间值“1”塔桥
指数式比大小
①底数相同(指数不同)
借助指数函数单调性比大小
②底数不同(指数不同)
借助中间值,如与“1”比较大小 (搭桥法)
归纳总结
例3 若函数f(x)=2ax+m-n(a>0,且a≠1)的图象恒过点(-1,4),则m+n等于( )
A.3 B.1 C.-1 D.-2
解析:由函数f(x)=2ax+m-n(a>0,且a≠1)的图象恒过(-1,4),
得m-1=0,2·am-1-n=4,
解得m=1,n=-2,
∴m+n=-1.
C
∴3x-1≥-1,∴x≥0,
故原不等式的解集是{x|x≥0}.
解:
解:设g(x)=x2+2(a-1)x+2,指数函数h(x)=在R上单调递减,
根据复合函数单调性同增异减的原则可知函数g(x)=x2+2(a-1)x+2在区间
(-∞,4]上单调递减.
由于函数g(x)=x2+2(a-1)x+2的图象开口向上,且对称轴为直线x=1-a,
要使函数f(x)在区间(-∞,4]上单调递增,则4≤1-a,即a≤-3.
故a的取值范围为(-∞,-3].
课堂总结
a的范围 0
图象
性质 定义域 值域 定点 单调性
函数值
若x>0, 则y>1
若x<0, 则0
R
(0,+∞)
(0,1)
增函数
减函数
O
x
y
1
O
x
y
1
指数函数
当堂检测
1.函数 y=2-x 的大致图象是( )
B
2.已知指数函数y=(2a-1)x 为减函数,则a的取值范围为_____________.
当堂检测
3. 用“”或“<”填空
(1) 3.10.5 ____ 3.12.3
(2) ____
(3)
(4)2.3-2.5 ____ 0.2-0.1
<
<
<
当堂检测
4. 如果 a-5x > ax+7 (a>0,且a≠1),求x的取值范围.
解 :① 当 时,-5x x+7,则 x
② 当 时, -5xx+7,则 x
综上,当 时,
当 时,
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
