新人教版九年级下数学27-1《图形的相似》课件
文档属性
| 名称 | 新人教版九年级下数学27-1《图形的相似》课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-01 00:00:00 | ||
图片预览



文档简介
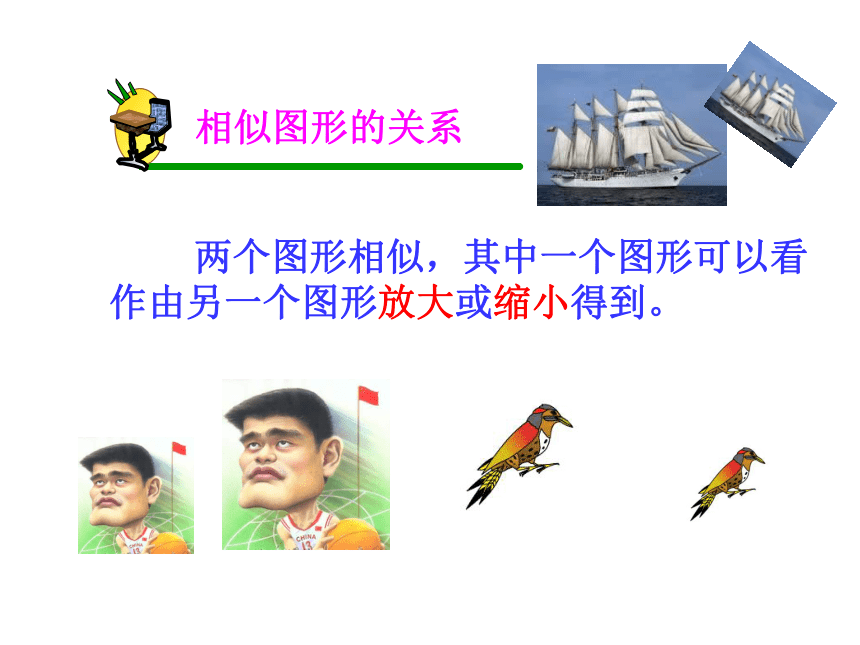
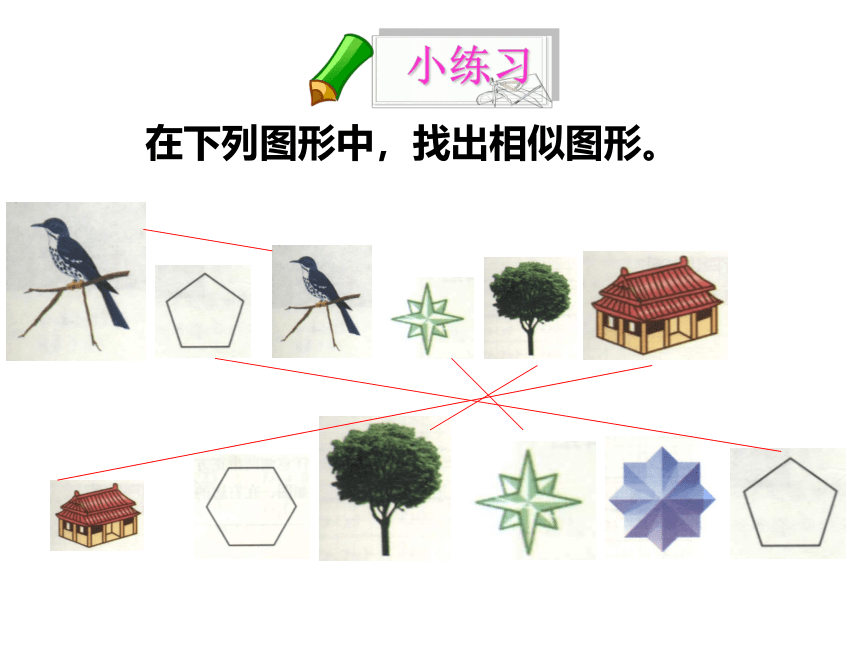
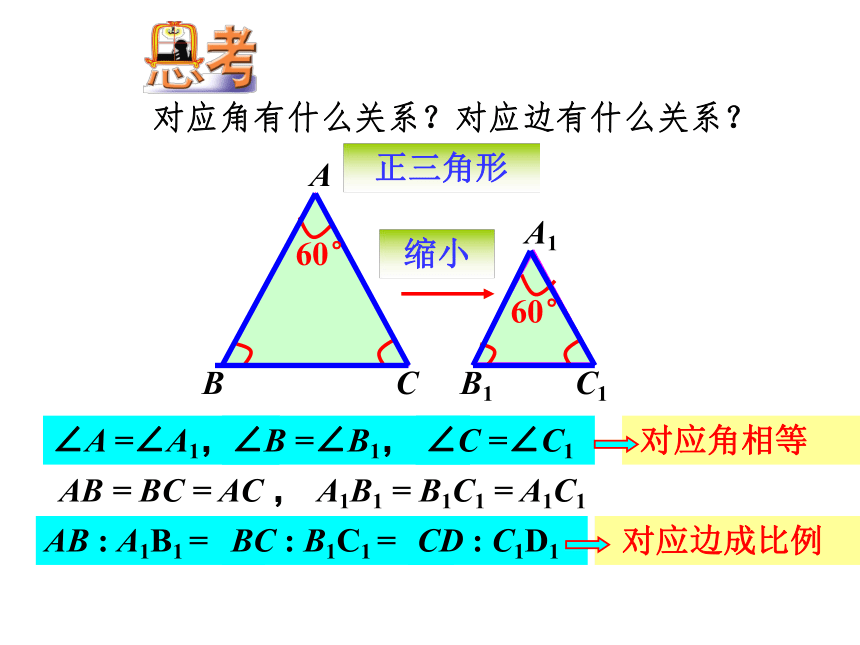
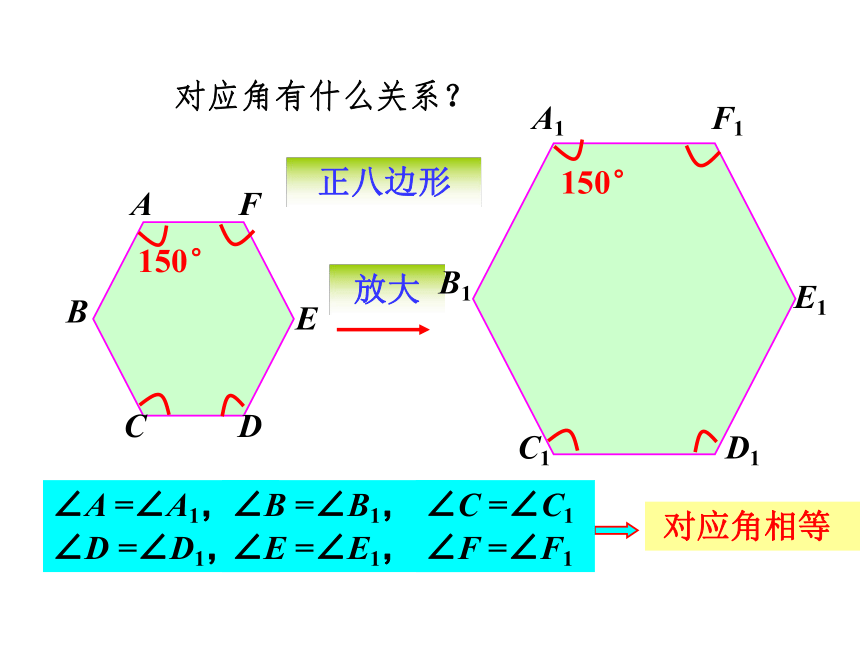
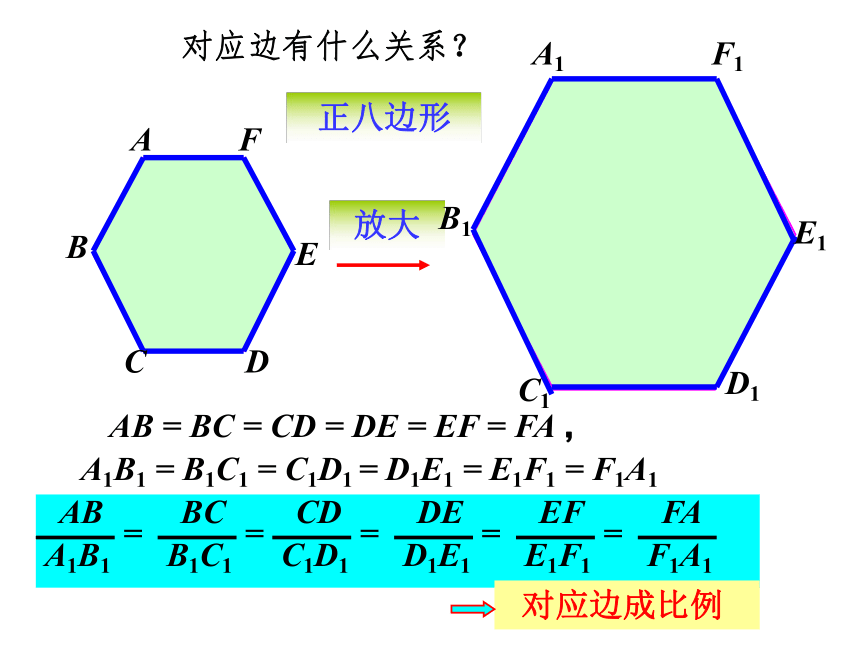
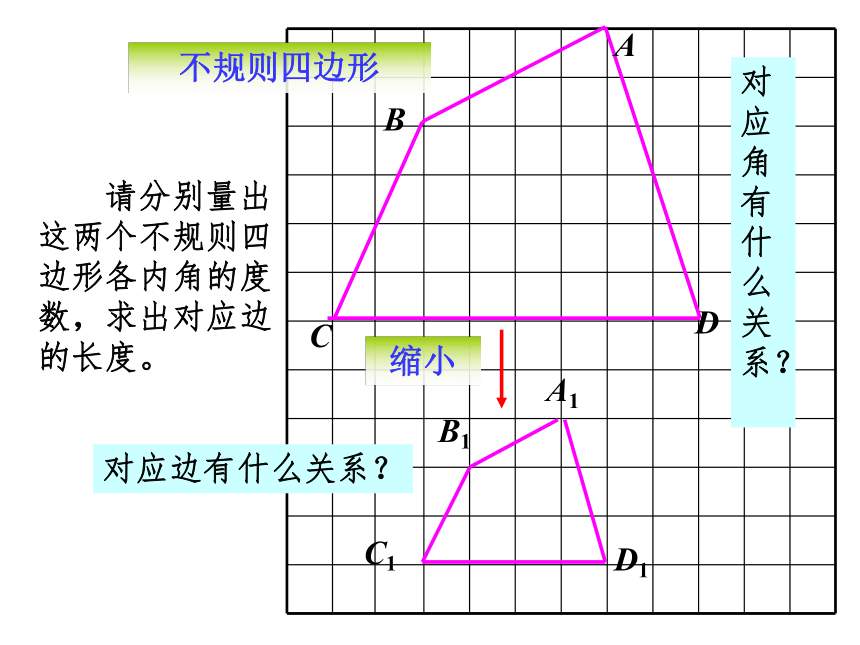
课件29张PPT。 两个图形的形状 ________,但图形的大小位置 __________,这样的图形叫做相似图形。完全相同不一定相同 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。相似图形的关系在下列图形中,找出相似图形。小练习相似多边形这两个图案中,有没有相似的图形? 这个零件中,有没有相似的图形? 根据相似多边形的特征,给相似多边形下定义。ABCA1B1C1正三角形缩小对应角有什么关系?对应边有什么关系?∠A =∠A1,∠B =∠B1,∠C =∠C1AB : A1B1 =BC : B1C1 =CD : C1D1AB = BC = AC ,A1B1 = B1C1 = A1C160°60° 对应角相等 对应边成比例正八边形放大对应角有什么关系?150°150°∠A =∠A1,∠B =∠B1,∠C =∠C1 对应角相等ABCA1B1C1FEDF1E1D1∠D =∠D1,∠E =∠E1,∠F =∠F1正八边形放大对应边有什么关系?ABCA1B1C1FEDF1E1D1AB = BC = CD = DE = EF = FA ,A1B1 = B1C1 = C1D1 = D1E1 = E1F1 = F1A1 对应边成比例=====ABCDA1B1C1D1 请分别量出这两个不规则四边形各内角的度数,求出对应边的长度。对应角有什么关系?对应边有什么关系?不规则四边形缩小 相似多边形(对应边的比相等)相似比相似多边形对应边的比。(k > 0) 若相似比k =1 ,相似图形有什么关系?对应角相等,对应边成比例。全等是一种特殊的相似。当相似比k =1时, 相似图形即是全等图形。 六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为 k1= 2 : 1, 对应边 AB:A1B1= 2 : 1 。 六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为 k2= 1 : 2, 对应边 AB:A1B1= 1 : 2 。相似比与叙述的顺序有关。相似多边形 各对应角相等、各对应边成比例的多边形叫做相似多边形. 对应角相等。
对应边成比例。两个多边形相似的条件相似六边形题型1 判断两个多边形是否相似3正方形344菱形解: ∵ 正方形,菱形的四条边都相等.
∴ 它们的对应边成比例,k = 3 : 4.
∵ 正方形的四个内角均为直角,而菱形的内角有钝角有锐角.
∴ 它们的对应角不相等.
∴ 这一组图形不相似.3正方形368长方形解:∵ 正方形和矩形的四个内角都是直角.
∴ 它们的对应角相等.
∵ 对应边 3 : 6 ≠ 3 : 8.
∴ 它们的对应边不成比例.
∴ 这一组图形不相似.解: ∵ 矩形的每个内角都等于90o.
∴ ∠A =∠E = 90°,∠B =∠F = 90°
∠C =∠G = 90°,∠D =∠H = 90°
∴ 它们的对应角相等.
∵ EH:AD=300:(300+2×7.5)=20/21.
EF:AB =150:(150+2×7.5)=10/11.
∴ EH:AD≠EF:AB.
∴ 它们的对应边不成比例.
∴ 矩形ABCD和矩形EFGH不相似. 一块长 3m,宽1.5m的矩形黑板,镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗?为什么?题型2 求相似多边形的对应角或对应边 五边形ABCDE相似于五边形FGHIJ,且AB=2cm,CD=3cm,DE=2.2cm,GH=6cm,HI =5cm,FJ=4cm, ∠A=120°,∠H=90°
求:(1)相似比等于多少?
(2)FG,IJ,BC,AE, ∠F, ∠CABCDEFGHIJ5解:(1)相似比=CD : HI=3 : 5
(2)∵五边形ABCDE相似于五边形FGHIJ
∴ ∠F =∠A=120o, ∠C= ∠H=90o,
∴AB : FG = BC : GH = CD : HI = DE : IJ = EA : JF
即2 : FG = BC : 6 = 3/5 = 2.2 : IJ = AE :4
解得FG =10/3 cm, BC =18/5cm,IJ=11/3cm,AE=12/5cmABCDEFGHIJ232.2654120°你能找出其中的相似多边形吗?相似正五边形相似正六边形相似正八边形相似正十二边形课堂小结1. 相似图形:形状相同的图形。2. 相似多边形:对应角相等,对应边成比例。相似多边形对应边的比。3. 相似比:随堂练习 1. 判断:
(1)任意两个矩形都是相似图形( )
(2)任意两个圆形是相似图形( )
(3)对应角相等的两个四边形是相似多边形( )
(4)两个正五边形是相似多边形( )
(5)两个全等三角形是相似多边形( )
(6)两菱形是相似多边形( )
(7)两个相似多边形,对应边成比例( ) √√√×√×× 2. 五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3,(1)若∠D=135°,则∠D′= ______。
(2)若A′B′=15cm,则AB= ______。135°5 3. 一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______ 。 18 4. 如图所示的两个矩形相似吗?为什么?
如果相似,相似比是多少?解;矩形ABCD相似于矩形EFGH因为它们的对应角相等,对应边成比例。相似比为:
对应边成比例。两个多边形相似的条件相似六边形题型1 判断两个多边形是否相似3正方形344菱形解: ∵ 正方形,菱形的四条边都相等.
∴ 它们的对应边成比例,k = 3 : 4.
∵ 正方形的四个内角均为直角,而菱形的内角有钝角有锐角.
∴ 它们的对应角不相等.
∴ 这一组图形不相似.3正方形368长方形解:∵ 正方形和矩形的四个内角都是直角.
∴ 它们的对应角相等.
∵ 对应边 3 : 6 ≠ 3 : 8.
∴ 它们的对应边不成比例.
∴ 这一组图形不相似.解: ∵ 矩形的每个内角都等于90o.
∴ ∠A =∠E = 90°,∠B =∠F = 90°
∠C =∠G = 90°,∠D =∠H = 90°
∴ 它们的对应角相等.
∵ EH:AD=300:(300+2×7.5)=20/21.
EF:AB =150:(150+2×7.5)=10/11.
∴ EH:AD≠EF:AB.
∴ 它们的对应边不成比例.
∴ 矩形ABCD和矩形EFGH不相似. 一块长 3m,宽1.5m的矩形黑板,镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗?为什么?题型2 求相似多边形的对应角或对应边 五边形ABCDE相似于五边形FGHIJ,且AB=2cm,CD=3cm,DE=2.2cm,GH=6cm,HI =5cm,FJ=4cm, ∠A=120°,∠H=90°
求:(1)相似比等于多少?
(2)FG,IJ,BC,AE, ∠F, ∠CABCDEFGHIJ5解:(1)相似比=CD : HI=3 : 5
(2)∵五边形ABCDE相似于五边形FGHIJ
∴ ∠F =∠A=120o, ∠C= ∠H=90o,
∴AB : FG = BC : GH = CD : HI = DE : IJ = EA : JF
即2 : FG = BC : 6 = 3/5 = 2.2 : IJ = AE :4
解得FG =10/3 cm, BC =18/5cm,IJ=11/3cm,AE=12/5cmABCDEFGHIJ232.2654120°你能找出其中的相似多边形吗?相似正五边形相似正六边形相似正八边形相似正十二边形课堂小结1. 相似图形:形状相同的图形。2. 相似多边形:对应角相等,对应边成比例。相似多边形对应边的比。3. 相似比:随堂练习 1. 判断:
(1)任意两个矩形都是相似图形( )
(2)任意两个圆形是相似图形( )
(3)对应角相等的两个四边形是相似多边形( )
(4)两个正五边形是相似多边形( )
(5)两个全等三角形是相似多边形( )
(6)两菱形是相似多边形( )
(7)两个相似多边形,对应边成比例( ) √√√×√×× 2. 五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3,(1)若∠D=135°,则∠D′= ______。
(2)若A′B′=15cm,则AB= ______。135°5 3. 一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______ 。 18 4. 如图所示的两个矩形相似吗?为什么?
如果相似,相似比是多少?解;矩形ABCD相似于矩形EFGH因为它们的对应角相等,对应边成比例。相似比为:
