3.1.1 课时2 区间与同一函数 课件 (共22张PPT) 2024~2025学年高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.1.1 课时2 区间与同一函数 课件 (共22张PPT) 2024~2025学年高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
3.1.1 课时2
区间与同一函数
学习目标
1.能正确使用区间表示数集.
2.会求一些简单函数的定义域与函数值.
3.求抽象函数定义域.
4.会判断两个函数是否为同一个函数.
5.求函数的值域.
知识回顾
设A、B为非空实数集,若对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,则称 f :A→B为从集合A到集合B的一个函数,
记作: y=f (x), x∈A.
函数的三要素:定义域、对应关系、值域.
新课讲授
阅读课本64-65页回答以下问题:
(1)什么是闭区间?
(2)什么是开区间?
(3)什么是半开半闭区间?
概念讲解
设a,b是两个实数,而且a⒈满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为[a,b];
⒉满足不等式a⒊满足不等式a≤x这里的实数a,b叫做相应区间的端点.
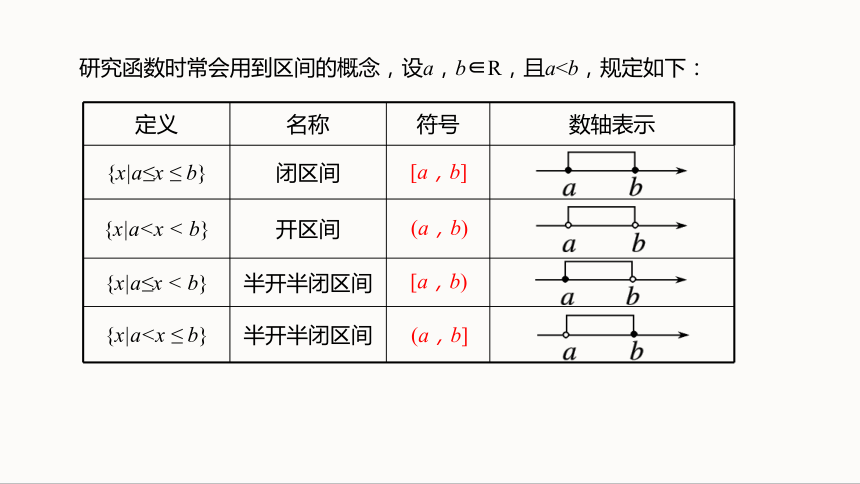
定义 名称 符号 数轴表示
{x|a≤x ≤ b} 闭区间
{x|a{x|a≤x < b} 半开半闭区间
{x|a[a,b]
(a,b)
[a,b)
(a,b]
研究函数时常会用到区间的概念,设a,b∈R,且a定义 名称 符号 数轴表示
{x|x≥a} 半开半闭区间
{x|x >a} 开区间
{x|x≤b} 半开半闭区间
{x|x研究函数时常会用到区间的概念,设a,b∈R,且a[a,+∞)
(a,+∞)
(-∞,b]
(-∞,b)
实数集R可以表示为(-∞,+ ∞)
1.区间是集合,只能表示无限集.
3.区间不能表示不连续的数集.
2.区间(a,b)的左端点必小于右端点,必须有a<b.
6.以“-∞”或“+∞”为区间的一端时,这一端必须是小括号.
5.区间都可以用数轴表示.
4.区间中的元素都是数字,并且有无限多个.
注意点
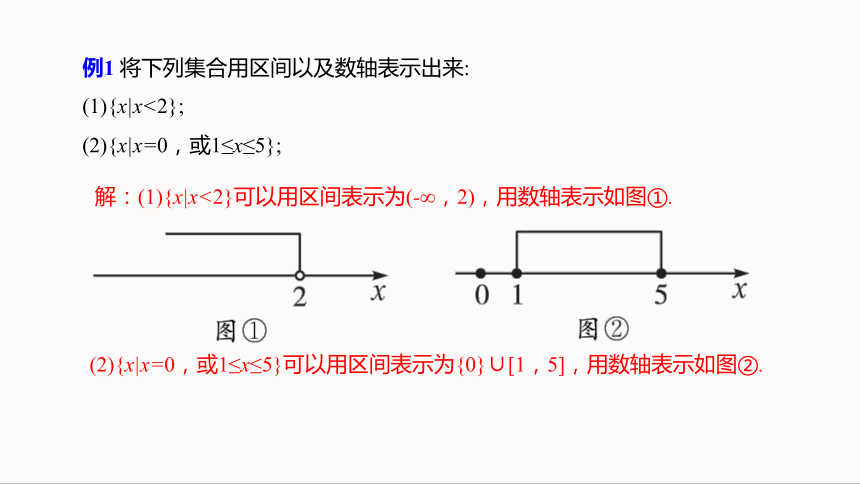
例1 将下列集合用区间以及数轴表示出来:
(1){x|x<2};
(2){x|x=0,或1≤x≤5};
解:(1){x|x<2}可以用区间表示为(-∞,2),用数轴表示如图①.
(2){x|x=0,或1≤x≤5}可以用区间表示为{0}∪[1,5],用数轴表示如图②.
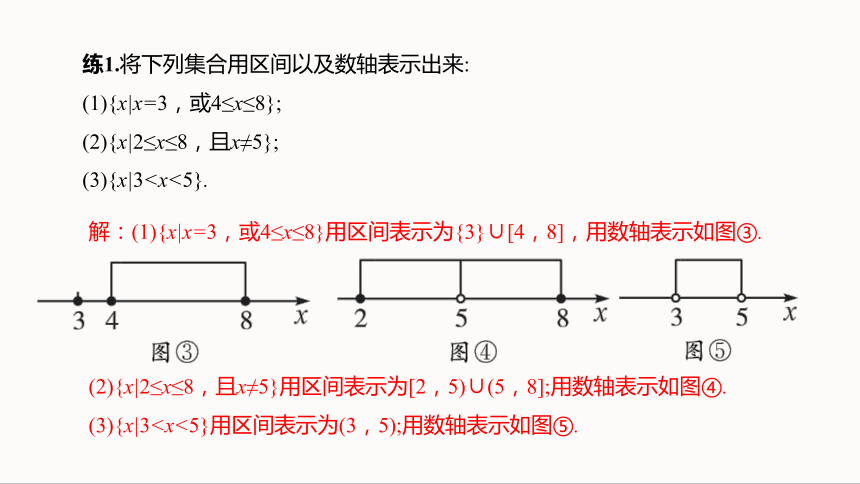
解:(1){x|x=3,或4≤x≤8}用区间表示为{3}∪[4,8],用数轴表示如图③.
(2){x|2≤x≤8,且x≠5}用区间表示为[2,5)∪(5,8];用数轴表示如图④.
(3){x|3练1.将下列集合用区间以及数轴表示出来:
(1){x|x=3,或4≤x≤8};
(2){x|2≤x≤8,且x≠5};
(3){x|3所以f(x)的定义域为[1,+∞).
[1,+∞)
归纳总结
求函数定义域的准则一般有:
(ⅰ)分式的分母不为0;
(ⅱ)偶次根式的被开方数非负;
(ⅲ)y=x0要求x≠0.
(1)求f(2),g(2)的值;
(2)求f(g(3))的值.
练2.若f(x)=2x-1,则f(f(x))等于( )
A.2x-1 B.4x-2
C.4x-3 D.2x-3
C
例4 (1)函数y=f(x)的定义域是[-1,3],则f(2x+1)的定义域为________.
(2)若函数y=f(3x+1)的定义域为[-2,4],则y=f(x)的定义域是( )
A.[-1,1] B.[-5,13]
C.[-5,1] D.[-1,13]
[-1,1]
分析:(1)令-1≤2x+1≤3,解得-1≤x≤1,
所以f(2x+1)的定义域为[-1,1].
(2)由题意知,-2≤x≤4,所以-5≤3x+1≤13,
所以y=f(x)的定义域是[-5,13].
B
练3.已知函数f(x-1)的定义域为{x|-2≤x≤3},则函数f(2x+1)的定义域为( )
A.{x|-1≤x≤9} B.{x|-3≤x≤7}
C.{x|-2≤x≤1} D.
D
例5 下列各组函数中是同一个函数的是( )
A.y=x+1与y=
B.y=x2+1与s=t2+1
C.y=2x与y=2x(x≥0)
D.y=(x+1)2与y=x2
B
判断两个函数为同一个函数应注意的三点:
(1)定义域、对应关系两者中只要有一个不相同就不是同一个函数,即使定义域与值域都相同,也不一定是同一个函数.
(2)函数是两个数集之间的对应关系,所以用什么字母表示自变量、因变量是没有限制的.
(3)在化简解析式时,必须是等价变形.
归纳总结
例6 求下列函数值域.
(1)f(x)=;(2)f(x)=x2+4x-1,x∈[0,3];(3)f(x)=;(4)f(x)=.
解:(1)∵x∈R时,x2≥0,∴1+x2≥1,
∴0<≤1,
∴f(x)的值域为(0,1].
(2)∵f(x)=(x+2)2-5,x∈[0,3],
结合图象知f(x)min=f(0)=-1,f(x)max=f(3)=20,
∴f(x)的值域为[-1,20].
求函数值域的方法——观察法
求函数值域的方法——配方法(二次函数型)
(3)f(x)=;(4)f(x)=.
(3)f(x)===2-,
∵x+1≠0,∴≠0,∴2-≠2,
∴f(x)的值域为(-∞,2)∪(2,+∞).
(4)令t=,
∵x≥1,∴t≥0,且x=t2+1,
∴原函数转化为g(t)=t2+1+t=(t+)2+,
∴结合图象知g(t)min=g(0)=1,即g(t)≥1,
∴f(x)的值域为[1,+∞).
求函数值域的方法——分离常数法
求函数值域的方法——换元法
注意新元的范围
课堂总结
回顾本节课,回答下列问题:
(1)区间如何表示?
(2)如何求简单函数的定义域和函数值?
(3)如何求抽象函数定义域?
(4)如何判断是否为同一个函数?
(5)如何求函数的值域?
当堂检测
1.下列函数中与y=x是同一个函数的是( )
B
2.下列各组函数是同一函数的是 (填序号).
②③
当堂检测
3.求下列函数的值域:
(1); (2)y=x2-4x+6(1≤x≤5).
y∈[2,11]
y∈[0,4]
3.1.1 课时2
区间与同一函数
学习目标
1.能正确使用区间表示数集.
2.会求一些简单函数的定义域与函数值.
3.求抽象函数定义域.
4.会判断两个函数是否为同一个函数.
5.求函数的值域.
知识回顾
设A、B为非空实数集,若对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,则称 f :A→B为从集合A到集合B的一个函数,
记作: y=f (x), x∈A.
函数的三要素:定义域、对应关系、值域.
新课讲授
阅读课本64-65页回答以下问题:
(1)什么是闭区间?
(2)什么是开区间?
(3)什么是半开半闭区间?
概念讲解
设a,b是两个实数,而且a
⒉满足不等式a
定义 名称 符号 数轴表示
{x|a≤x ≤ b} 闭区间
{x|a
{x|a
(a,b)
[a,b)
(a,b]
研究函数时常会用到区间的概念,设a,b∈R,且a
{x|x≥a} 半开半闭区间
{x|x >a} 开区间
{x|x≤b} 半开半闭区间
{x|x
(a,+∞)
(-∞,b]
(-∞,b)
实数集R可以表示为(-∞,+ ∞)
1.区间是集合,只能表示无限集.
3.区间不能表示不连续的数集.
2.区间(a,b)的左端点必小于右端点,必须有a<b.
6.以“-∞”或“+∞”为区间的一端时,这一端必须是小括号.
5.区间都可以用数轴表示.
4.区间中的元素都是数字,并且有无限多个.
注意点
例1 将下列集合用区间以及数轴表示出来:
(1){x|x<2};
(2){x|x=0,或1≤x≤5};
解:(1){x|x<2}可以用区间表示为(-∞,2),用数轴表示如图①.
(2){x|x=0,或1≤x≤5}可以用区间表示为{0}∪[1,5],用数轴表示如图②.
解:(1){x|x=3,或4≤x≤8}用区间表示为{3}∪[4,8],用数轴表示如图③.
(2){x|2≤x≤8,且x≠5}用区间表示为[2,5)∪(5,8];用数轴表示如图④.
(3){x|3
(1){x|x=3,或4≤x≤8};
(2){x|2≤x≤8,且x≠5};
(3){x|3
[1,+∞)
归纳总结
求函数定义域的准则一般有:
(ⅰ)分式的分母不为0;
(ⅱ)偶次根式的被开方数非负;
(ⅲ)y=x0要求x≠0.
(1)求f(2),g(2)的值;
(2)求f(g(3))的值.
练2.若f(x)=2x-1,则f(f(x))等于( )
A.2x-1 B.4x-2
C.4x-3 D.2x-3
C
例4 (1)函数y=f(x)的定义域是[-1,3],则f(2x+1)的定义域为________.
(2)若函数y=f(3x+1)的定义域为[-2,4],则y=f(x)的定义域是( )
A.[-1,1] B.[-5,13]
C.[-5,1] D.[-1,13]
[-1,1]
分析:(1)令-1≤2x+1≤3,解得-1≤x≤1,
所以f(2x+1)的定义域为[-1,1].
(2)由题意知,-2≤x≤4,所以-5≤3x+1≤13,
所以y=f(x)的定义域是[-5,13].
B
练3.已知函数f(x-1)的定义域为{x|-2≤x≤3},则函数f(2x+1)的定义域为( )
A.{x|-1≤x≤9} B.{x|-3≤x≤7}
C.{x|-2≤x≤1} D.
D
例5 下列各组函数中是同一个函数的是( )
A.y=x+1与y=
B.y=x2+1与s=t2+1
C.y=2x与y=2x(x≥0)
D.y=(x+1)2与y=x2
B
判断两个函数为同一个函数应注意的三点:
(1)定义域、对应关系两者中只要有一个不相同就不是同一个函数,即使定义域与值域都相同,也不一定是同一个函数.
(2)函数是两个数集之间的对应关系,所以用什么字母表示自变量、因变量是没有限制的.
(3)在化简解析式时,必须是等价变形.
归纳总结
例6 求下列函数值域.
(1)f(x)=;(2)f(x)=x2+4x-1,x∈[0,3];(3)f(x)=;(4)f(x)=.
解:(1)∵x∈R时,x2≥0,∴1+x2≥1,
∴0<≤1,
∴f(x)的值域为(0,1].
(2)∵f(x)=(x+2)2-5,x∈[0,3],
结合图象知f(x)min=f(0)=-1,f(x)max=f(3)=20,
∴f(x)的值域为[-1,20].
求函数值域的方法——观察法
求函数值域的方法——配方法(二次函数型)
(3)f(x)=;(4)f(x)=.
(3)f(x)===2-,
∵x+1≠0,∴≠0,∴2-≠2,
∴f(x)的值域为(-∞,2)∪(2,+∞).
(4)令t=,
∵x≥1,∴t≥0,且x=t2+1,
∴原函数转化为g(t)=t2+1+t=(t+)2+,
∴结合图象知g(t)min=g(0)=1,即g(t)≥1,
∴f(x)的值域为[1,+∞).
求函数值域的方法——分离常数法
求函数值域的方法——换元法
注意新元的范围
课堂总结
回顾本节课,回答下列问题:
(1)区间如何表示?
(2)如何求简单函数的定义域和函数值?
(3)如何求抽象函数定义域?
(4)如何判断是否为同一个函数?
(5)如何求函数的值域?
当堂检测
1.下列函数中与y=x是同一个函数的是( )
B
2.下列各组函数是同一函数的是 (填序号).
②③
当堂检测
3.求下列函数的值域:
(1); (2)y=x2-4x+6(1≤x≤5).
y∈[2,11]
y∈[0,4]
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
