3.4 函数的应用(一) 课件(共15张PPT) 2024~2025学年高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.4 函数的应用(一) 课件(共15张PPT) 2024~2025学年高一数学人教A版(2019)必修第一册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 724.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
3.4 函数的应用(一)
学习目标
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律.
3.会应用函数模型解决一些简单的实际问题.
情境引入
我们学习了哪些函数 (并用自己的语言描述它们的性质)
常见函数模型 一次函数
二次函数
幂函数型
分段函数
例1 一辆汽车在某段路程中行驶的平均速率 v (单位:km/h)与时间 t (单位:h)的关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时,汽车的里程表读数 s(单位:km)与时间 t 的函数解析式,并画出相应的图象.
例题讲解
分析:当时间t在[0,5]内变化时,对于任意的时刻t都有唯一确定的行驶路程与之对应. 根据图3.4-1在时间段[0,1), [1,2), [2,3), [3,4), [4,5]内行驶的平均速率分别为50 km/h,80 km/h,90 km/h,75 km/h ,65 km/h ,因此在每个时间段内,行驶路程与时间的关系也不一样,需要分段表述.
解:(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360,
阴影部分的面积表示汽车在这5 h 内行驶的路程为360 km.
(2)根据图有
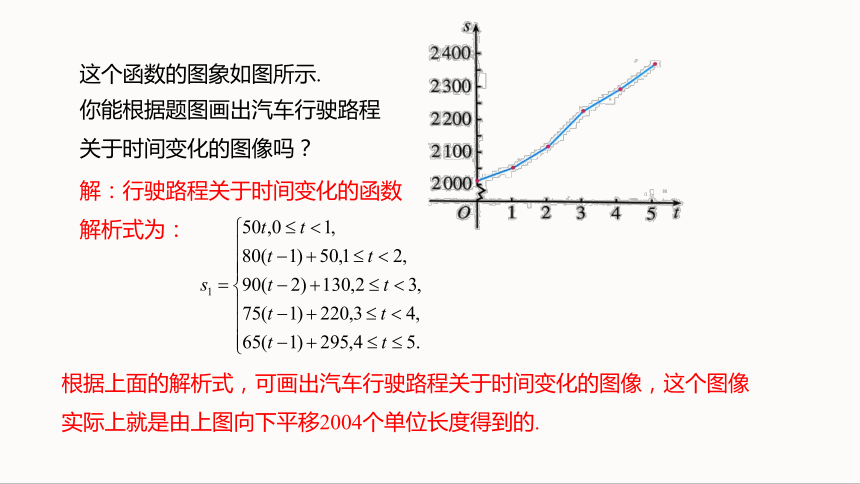
这个函数的图象如图所示.
你能根据题图画出汽车行驶路程关于时间变化的图像吗?
解:行驶路程关于时间变化的函数解析式为:
根据上面的解析式,可画出汽车行驶路程关于时间变化的图像,这个图像实际上就是由上图向下平移2004个单位长度得到的.
归纳总结
解函数应用题的方法和步骤:
1.审题:(1)设出未知量;
(2)找出量与量的关系.
2.建模:建立函数关系式.
3.求解:用数学方法解出未知量.
4.回归实际:检验所求结果是否符合实际并作答.
例2 某报刊亭从报社买进报纸的价格是每份0.24元,卖出的价格是每份0.40元,卖不掉的报纸可以以每份0.08元的价格退回报社.在一个月(以30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的报纸份数必须相同,试问报刊亭摊主应该每天从报社买进多少份报纸,才能使每月所获利润最大.
解:设每天从报社买进x份(250≤x≤400)报纸,每月所获利润是y元,
则每月售出报纸共(20x+10×250)份,每月退回报社报纸共10×(x-250)份.
依题意得,y=(0.40-0.24)×(20x+10×250)-(0.24-0.08)×10(x-250).
即y=0.16(20x+2 500)-0.16(10x-2 500),
化简得y=1.6x+800,其中250≤x≤400,
因为此一次函数的k=1.6>0,
所以y是一个在定义域内单调递增的函数,
再由250≤x≤400知,当x=400时,y取得最大值,
此时y=1.6×400+800=1 440(元).
所以买进400份报纸所获利润最大,获利1 440元.
例2 某报刊亭从报社买进报纸的价格是每份0.24元,卖出的价格是每份0.40元,卖不掉的报纸可以以每份0.08元的价格退回报社.在一个月(以30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的报纸份数必须相同,试问报刊亭摊主应该每天从报社买进多少份报纸,才能使每月所获利润最大.
例3 某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
解:根据题意,得y=90-3(x-50),化简,得y=-3x+240(50≤x≤55,x∈N).
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
解:因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.
所以w=(x-40)(-3x+240)=-3x2+360x-9 600(50≤x≤55,x∈N).
例3 某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(3)当每箱苹果的售价为多少元时,可以获得最大利润?最大利润是多少?
解:因为w=-3x2+360x-9 600
=-3(x-60)2+1 200,
所以当x<60时,w随x的增大而增大.
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1125.
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1125元.
课堂总结
实际问题
建立函数模型
问题结果
数学源于生活,用于生活
当堂检测
1.为了引导居民节约用电,某城市对居民生活用电实行“阶梯电价”,按月用电量计算,将居民家庭每月用电量划分为三个阶梯,电价按阶梯递增.第一阶梯:月用电量不超过240千瓦时的部分,电价为0.5元/千瓦时;第二阶梯:月用电量超过240千瓦时但不超过400千瓦时的部分,电价为0.6元/千瓦时;第三阶梯:月用电量超过400千瓦时的部分,电价为0.8元/千瓦时.若某户居民10月份交纳的电费为360元,则此户居民10月份的用电量为 千瓦时.
580
2.生产一定数量商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为 x2+2x+20万元,商品的售价是每件20元,为获取最大利润(利润=收入-成本),该企业一个月应生产该商品数量为( )
A.9万件 B.18万件
C.22万件 D.36万件
B
3. 某汽车运输公司购买了一批豪华大客车投入运营,据市场分析,每辆客车营运的利润y与营运年数x(x∈N)为二次函数关系(如图),则客车经过___年可使营运的年平均利润最大.
5
3.4 函数的应用(一)
学习目标
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数类型刻画现实问题的变化规律.
3.会应用函数模型解决一些简单的实际问题.
情境引入
我们学习了哪些函数 (并用自己的语言描述它们的性质)
常见函数模型 一次函数
二次函数
幂函数型
分段函数
例1 一辆汽车在某段路程中行驶的平均速率 v (单位:km/h)与时间 t (单位:h)的关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时,汽车的里程表读数 s(单位:km)与时间 t 的函数解析式,并画出相应的图象.
例题讲解
分析:当时间t在[0,5]内变化时,对于任意的时刻t都有唯一确定的行驶路程与之对应. 根据图3.4-1在时间段[0,1), [1,2), [2,3), [3,4), [4,5]内行驶的平均速率分别为50 km/h,80 km/h,90 km/h,75 km/h ,65 km/h ,因此在每个时间段内,行驶路程与时间的关系也不一样,需要分段表述.
解:(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360,
阴影部分的面积表示汽车在这5 h 内行驶的路程为360 km.
(2)根据图有
这个函数的图象如图所示.
你能根据题图画出汽车行驶路程关于时间变化的图像吗?
解:行驶路程关于时间变化的函数解析式为:
根据上面的解析式,可画出汽车行驶路程关于时间变化的图像,这个图像实际上就是由上图向下平移2004个单位长度得到的.
归纳总结
解函数应用题的方法和步骤:
1.审题:(1)设出未知量;
(2)找出量与量的关系.
2.建模:建立函数关系式.
3.求解:用数学方法解出未知量.
4.回归实际:检验所求结果是否符合实际并作答.
例2 某报刊亭从报社买进报纸的价格是每份0.24元,卖出的价格是每份0.40元,卖不掉的报纸可以以每份0.08元的价格退回报社.在一个月(以30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的报纸份数必须相同,试问报刊亭摊主应该每天从报社买进多少份报纸,才能使每月所获利润最大.
解:设每天从报社买进x份(250≤x≤400)报纸,每月所获利润是y元,
则每月售出报纸共(20x+10×250)份,每月退回报社报纸共10×(x-250)份.
依题意得,y=(0.40-0.24)×(20x+10×250)-(0.24-0.08)×10(x-250).
即y=0.16(20x+2 500)-0.16(10x-2 500),
化简得y=1.6x+800,其中250≤x≤400,
因为此一次函数的k=1.6>0,
所以y是一个在定义域内单调递增的函数,
再由250≤x≤400知,当x=400时,y取得最大值,
此时y=1.6×400+800=1 440(元).
所以买进400份报纸所获利润最大,获利1 440元.
例2 某报刊亭从报社买进报纸的价格是每份0.24元,卖出的价格是每份0.40元,卖不掉的报纸可以以每份0.08元的价格退回报社.在一个月(以30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的报纸份数必须相同,试问报刊亭摊主应该每天从报社买进多少份报纸,才能使每月所获利润最大.
例3 某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
解:根据题意,得y=90-3(x-50),化简,得y=-3x+240(50≤x≤55,x∈N).
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
解:因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.
所以w=(x-40)(-3x+240)=-3x2+360x-9 600(50≤x≤55,x∈N).
例3 某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(3)当每箱苹果的售价为多少元时,可以获得最大利润?最大利润是多少?
解:因为w=-3x2+360x-9 600
=-3(x-60)2+1 200,
所以当x<60时,w随x的增大而增大.
又50≤x≤55,x∈N,所以当x=55时,w有最大值,最大值为1125.
所以当每箱苹果的售价为55元时,可以获得最大利润,且最大利润为1125元.
课堂总结
实际问题
建立函数模型
问题结果
数学源于生活,用于生活
当堂检测
1.为了引导居民节约用电,某城市对居民生活用电实行“阶梯电价”,按月用电量计算,将居民家庭每月用电量划分为三个阶梯,电价按阶梯递增.第一阶梯:月用电量不超过240千瓦时的部分,电价为0.5元/千瓦时;第二阶梯:月用电量超过240千瓦时但不超过400千瓦时的部分,电价为0.6元/千瓦时;第三阶梯:月用电量超过400千瓦时的部分,电价为0.8元/千瓦时.若某户居民10月份交纳的电费为360元,则此户居民10月份的用电量为 千瓦时.
580
2.生产一定数量商品的全部费用称为生产成本,某企业一个月生产某种商品x万件时的生产成本为 x2+2x+20万元,商品的售价是每件20元,为获取最大利润(利润=收入-成本),该企业一个月应生产该商品数量为( )
A.9万件 B.18万件
C.22万件 D.36万件
B
3. 某汽车运输公司购买了一批豪华大客车投入运营,据市场分析,每辆客车营运的利润y与营运年数x(x∈N)为二次函数关系(如图),则客车经过___年可使营运的年平均利润最大.
5
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
