高中数学人教A版(2019)必修第一册期中试卷(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册期中试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 51.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 22:14:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
高中数学人教A版(2019)必修第一册期中试卷
一、单选题
1.已知集合 ,则 ( )
A. B.
C. D.
2.已知集合,,则( )
A. B. C. D.
3.已知集合 A={x|x<1} ,
,则下列结论正确的是( )
A.
B.
C.
D.
4.一元二次不等式 的解集是( )
A. B. 或
C. D. 或
5.给出下列四个关系:π∈R, 0 Q ,0.7∈N, 0∈ ,其中正确的关系个数为( )
A.4 B.3 C.2 D.1
6.设集合,,则( )
A.{2} B. C. D.
7.函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.
8.函数f(x)= 的图象( )
A.关于原点对称 B.关于直线y=x对称
C.关于x轴对称 D.关于y轴对称
9.已知函数 的定义域为 ,则函数 的定义域为( )
A. B. C. D.
10.已知函数 是定义在 上的减函数,则实数 的取值范围为( )
A. B. C. D.
二、多选题
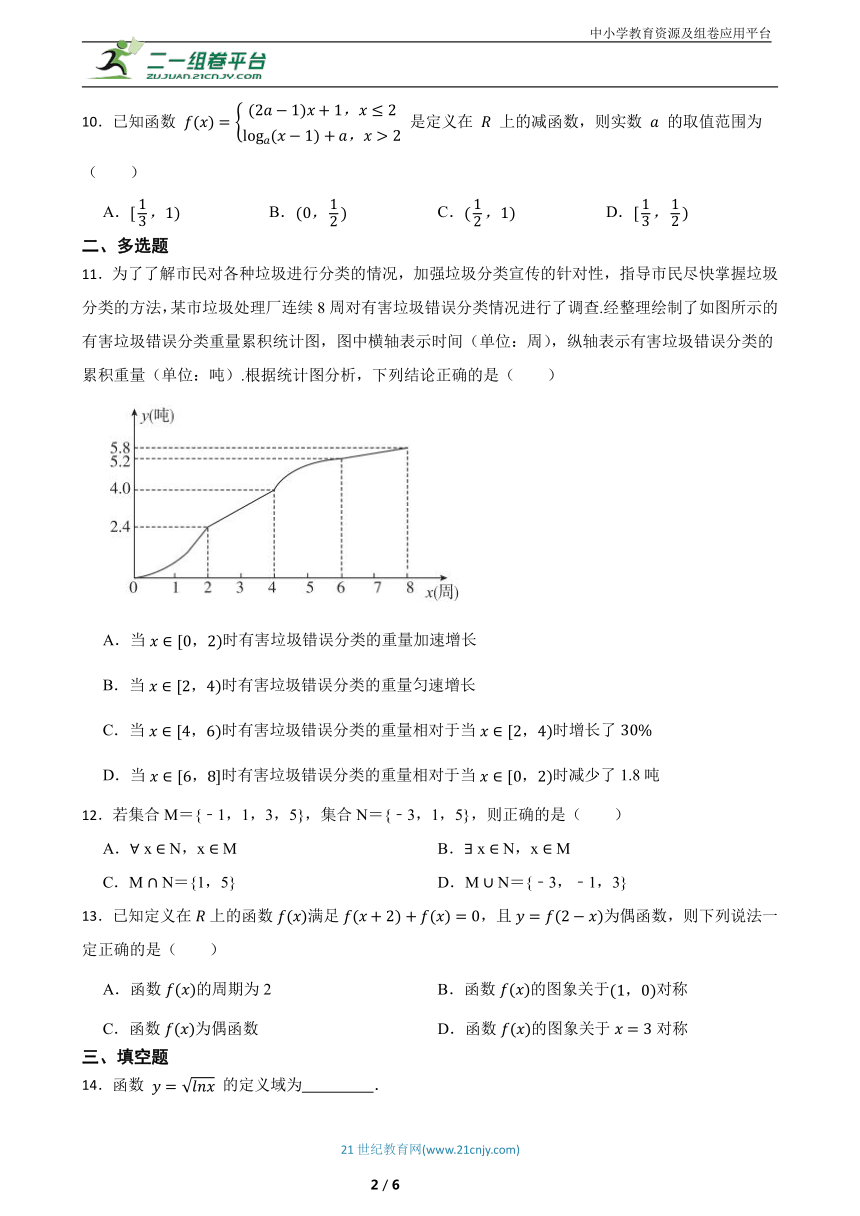
11.为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是( )
A.当时有害垃圾错误分类的重量加速增长
B.当时有害垃圾错误分类的重量匀速增长
C.当时有害垃圾错误分类的重量相对于当时增长了
D.当时有害垃圾错误分类的重量相对于当时减少了1.8吨
12.若集合M={﹣1,1,3,5},集合N={﹣3,1,5},则正确的是( )
A. x N,x M B. x N,x M
C.M N={1,5} D.M N={﹣3,﹣1,3}
13.已知定义在上的函数满足,且为偶函数,则下列说法一定正确的是( )
A.函数的周期为2 B.函数的图象关于对称
C.函数为偶函数 D.函数的图象关于对称
三、填空题
14.函数 的定义域为 .
15.已知集合,则 .
16.命题“ , ”的否定是 .
17.已知直线和平面,与存在位置关系M.若“且M”是“”的充分条件,则M可以是 .
18.若函数f(x)满足f(2x+1)=3﹣2x,则f(x)的解析式为 .
19.2021年湖北高考中政治、地理、化学、生物按照等级赋分,规则如下:原始分按照比例转换成A,B,C,D,E五个等级,然后利用等级赋分公式将原始分转换为赋分,例如B等级赋分公式如下: ,其中 为原始分, 为赋分, ( )为各等级原始分区间的下限和上限,小王地理考了81分, 等级为B,地理B等级原始分区间为 ,可以列式 ,计算出 79分即为赋分,假设高考中小明地理、化学原始分均为 ,等级均为B,地理B等级原始分区间为a~c,化学B等级原始分区间为b~c(b≥a),转换后,地理赋分为 ,化学赋分为 ,则 (空格处填“ ”或“ ”).
四、解答题
20.已知 ,非空集合 ,若 ,求实数 的取值范围.
21.已知函数 .
(1)求函数 的定义域和值域;
(2)判断函数 在区间 上单调性,并用定义来证明所得结论.
22.若 ,集合 .
求:
(1)a+b;
(2) .
23.已知函数 是关于 的偶函数.
(1)求 的值;
(2)求证: 对任意实数 ,函数 的图象与函数 的图象最多只有一个交点.
答案解析部分
1.【答案】A
【知识点】并集及其运算
2.【答案】C
【知识点】交集及其运算
3.【答案】A
【知识点】并集及其运算;交集及其运算
4.【答案】D
【知识点】一元二次不等式及其解法
5.【答案】D
【知识点】集合的含义;元素与集合的关系
6.【答案】B
【知识点】交集及其运算
7.【答案】D
【知识点】函数单调性的性质
8.【答案】D
【知识点】奇偶函数图象的对称性
9.【答案】D
【知识点】函数的定义域及其求法
10.【答案】D
【知识点】函数单调性的判断与证明;函数单调性的性质
11.【答案】A,B,D
【知识点】函数单调性的性质
12.【答案】B,C
【知识点】元素与集合的关系;并集及其运算;交集及其运算
13.【答案】B,C
【知识点】奇函数与偶函数的性质;奇偶函数图象的对称性
14.【答案】
【知识点】函数的定义域及其求法
15.【答案】{1}
【知识点】交集及其运算
16.【答案】 ,
【知识点】命题的否定
17.【答案】(或)
【知识点】充分条件
18.【答案】f(x)=4﹣x
【知识点】函数解析式的求解及常用方法
19.【答案】≥
【知识点】函数单调性的性质
20.【答案】解: ,
非空集合 ,
所以 ,即 ,
所以 ,
因为 是 的子集,
故 ,
解得 ,
故实数 的取值范围是
【知识点】集合间关系的判断
21.【答案】(1)解: ,
的定义域为 .值域
(2)解:由函数解析式得该函数在 为减函数,下面证明:
任取 ,且 ,
, , ,
.
函数在 为减函数
【知识点】函数的定义域及其求法;函数的值域;函数单调性的判断与证明
22.【答案】(1)解:∵ 是分母,
∴ ,
因此只能 ;
(2)解:由 得 ,即 ,
∴ , ,
∴ .
【知识点】集合中元素的确定性、互异性、无序性;集合相等
23.【答案】(1)解:因为f(x)是关于x的偶函数,
所以log2(2 - x + 1) + k( - x) = log2(2x + 1) + kx, 即2kx = log2 = - x, 解得k = -
(2)证明:由 , 得log2(2x + 1) - x = x + m,
所以 m = log2(2x + 1) -x = log2(1 + ). 令h(x) = log2(1 + ),
设x1, x2∈R, 且x1 < x2, 则 > , 所以log2(1 + ) > log2(1 + ),
所以h(x1) – h(x2) = log2(1 + ) - log2(1 + ) > 0, 即 h(x1) > h(x2), ∴ h(x)在R上单调递减.
因此, 函数y = h(x)的图象与直线y = m的图象最多只有一个交点. 所以, 对任意实数m, 函数y = f(x)的图象与直线y = x + m的图象最多只有一个交点
【知识点】函数单调性的判断与证明;奇函数与偶函数的性质
21世纪教育网(www.21cnjy.com)
1 / 1
高中数学人教A版(2019)必修第一册期中试卷
一、单选题
1.已知集合 ,则 ( )
A. B.
C. D.
2.已知集合,,则( )
A. B. C. D.
3.已知集合 A={x|x<1} ,
,则下列结论正确的是( )
A.
B.
C.
D.
4.一元二次不等式 的解集是( )
A. B. 或
C. D. 或
5.给出下列四个关系:π∈R, 0 Q ,0.7∈N, 0∈ ,其中正确的关系个数为( )
A.4 B.3 C.2 D.1
6.设集合,,则( )
A.{2} B. C. D.
7.函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.
8.函数f(x)= 的图象( )
A.关于原点对称 B.关于直线y=x对称
C.关于x轴对称 D.关于y轴对称
9.已知函数 的定义域为 ,则函数 的定义域为( )
A. B. C. D.
10.已知函数 是定义在 上的减函数,则实数 的取值范围为( )
A. B. C. D.
二、多选题
11.为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是( )
A.当时有害垃圾错误分类的重量加速增长
B.当时有害垃圾错误分类的重量匀速增长
C.当时有害垃圾错误分类的重量相对于当时增长了
D.当时有害垃圾错误分类的重量相对于当时减少了1.8吨
12.若集合M={﹣1,1,3,5},集合N={﹣3,1,5},则正确的是( )
A. x N,x M B. x N,x M
C.M N={1,5} D.M N={﹣3,﹣1,3}
13.已知定义在上的函数满足,且为偶函数,则下列说法一定正确的是( )
A.函数的周期为2 B.函数的图象关于对称
C.函数为偶函数 D.函数的图象关于对称
三、填空题
14.函数 的定义域为 .
15.已知集合,则 .
16.命题“ , ”的否定是 .
17.已知直线和平面,与存在位置关系M.若“且M”是“”的充分条件,则M可以是 .
18.若函数f(x)满足f(2x+1)=3﹣2x,则f(x)的解析式为 .
19.2021年湖北高考中政治、地理、化学、生物按照等级赋分,规则如下:原始分按照比例转换成A,B,C,D,E五个等级,然后利用等级赋分公式将原始分转换为赋分,例如B等级赋分公式如下: ,其中 为原始分, 为赋分, ( )为各等级原始分区间的下限和上限,小王地理考了81分, 等级为B,地理B等级原始分区间为 ,可以列式 ,计算出 79分即为赋分,假设高考中小明地理、化学原始分均为 ,等级均为B,地理B等级原始分区间为a~c,化学B等级原始分区间为b~c(b≥a),转换后,地理赋分为 ,化学赋分为 ,则 (空格处填“ ”或“ ”).
四、解答题
20.已知 ,非空集合 ,若 ,求实数 的取值范围.
21.已知函数 .
(1)求函数 的定义域和值域;
(2)判断函数 在区间 上单调性,并用定义来证明所得结论.
22.若 ,集合 .
求:
(1)a+b;
(2) .
23.已知函数 是关于 的偶函数.
(1)求 的值;
(2)求证: 对任意实数 ,函数 的图象与函数 的图象最多只有一个交点.
答案解析部分
1.【答案】A
【知识点】并集及其运算
2.【答案】C
【知识点】交集及其运算
3.【答案】A
【知识点】并集及其运算;交集及其运算
4.【答案】D
【知识点】一元二次不等式及其解法
5.【答案】D
【知识点】集合的含义;元素与集合的关系
6.【答案】B
【知识点】交集及其运算
7.【答案】D
【知识点】函数单调性的性质
8.【答案】D
【知识点】奇偶函数图象的对称性
9.【答案】D
【知识点】函数的定义域及其求法
10.【答案】D
【知识点】函数单调性的判断与证明;函数单调性的性质
11.【答案】A,B,D
【知识点】函数单调性的性质
12.【答案】B,C
【知识点】元素与集合的关系;并集及其运算;交集及其运算
13.【答案】B,C
【知识点】奇函数与偶函数的性质;奇偶函数图象的对称性
14.【答案】
【知识点】函数的定义域及其求法
15.【答案】{1}
【知识点】交集及其运算
16.【答案】 ,
【知识点】命题的否定
17.【答案】(或)
【知识点】充分条件
18.【答案】f(x)=4﹣x
【知识点】函数解析式的求解及常用方法
19.【答案】≥
【知识点】函数单调性的性质
20.【答案】解: ,
非空集合 ,
所以 ,即 ,
所以 ,
因为 是 的子集,
故 ,
解得 ,
故实数 的取值范围是
【知识点】集合间关系的判断
21.【答案】(1)解: ,
的定义域为 .值域
(2)解:由函数解析式得该函数在 为减函数,下面证明:
任取 ,且 ,
, , ,
.
函数在 为减函数
【知识点】函数的定义域及其求法;函数的值域;函数单调性的判断与证明
22.【答案】(1)解:∵ 是分母,
∴ ,
因此只能 ;
(2)解:由 得 ,即 ,
∴ , ,
∴ .
【知识点】集合中元素的确定性、互异性、无序性;集合相等
23.【答案】(1)解:因为f(x)是关于x的偶函数,
所以log2(2 - x + 1) + k( - x) = log2(2x + 1) + kx, 即2kx = log2 = - x, 解得k = -
(2)证明:由 , 得log2(2x + 1) - x = x + m,
所以 m = log2(2x + 1) -x = log2(1 + ). 令h(x) = log2(1 + ),
设x1, x2∈R, 且x1 < x2, 则 > , 所以log2(1 + ) > log2(1 + ),
所以h(x1) – h(x2) = log2(1 + ) - log2(1 + ) > 0, 即 h(x1) > h(x2), ∴ h(x)在R上单调递减.
因此, 函数y = h(x)的图象与直线y = m的图象最多只有一个交点. 所以, 对任意实数m, 函数y = f(x)的图象与直线y = x + m的图象最多只有一个交点
【知识点】函数单调性的判断与证明;奇函数与偶函数的性质
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
