21.5 反比例函数图像与性质课件
图片预览



文档简介
课件17张PPT。反比例函数的图象和性质复习提问1. 下列函数中哪些是反比例函数?
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1y = 2x2y = 3x2. 上节课我们学的反比例函数关系式是什么?
自变量x的取值范围是什么?
函数y的取值范围是什么?x≠0 ,y≠0(k ≠0,k是常数)已知一次函数y=kx+b(k≠0)的图象是大家想不想知道:反比例函数 (k≠0)的图象是什么样子呢?让我们一起画个反比例函数的图象看一看。一条直线回顾画出反比例函数 和
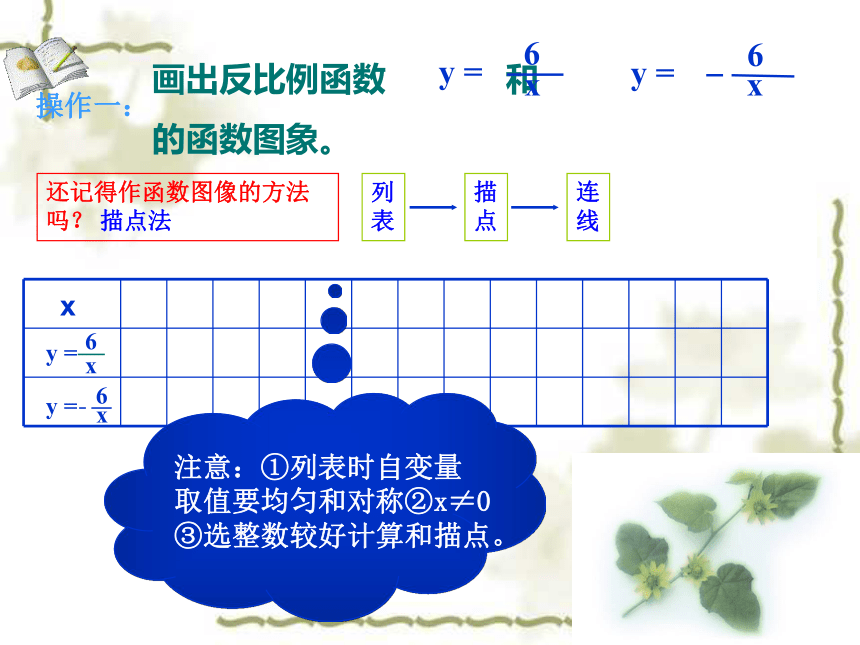
的函数图象。
列
表描
点连
线还记得作函数图像的方法吗? 描点法注意:①列表时自变量
取值要均匀和对称②x≠0
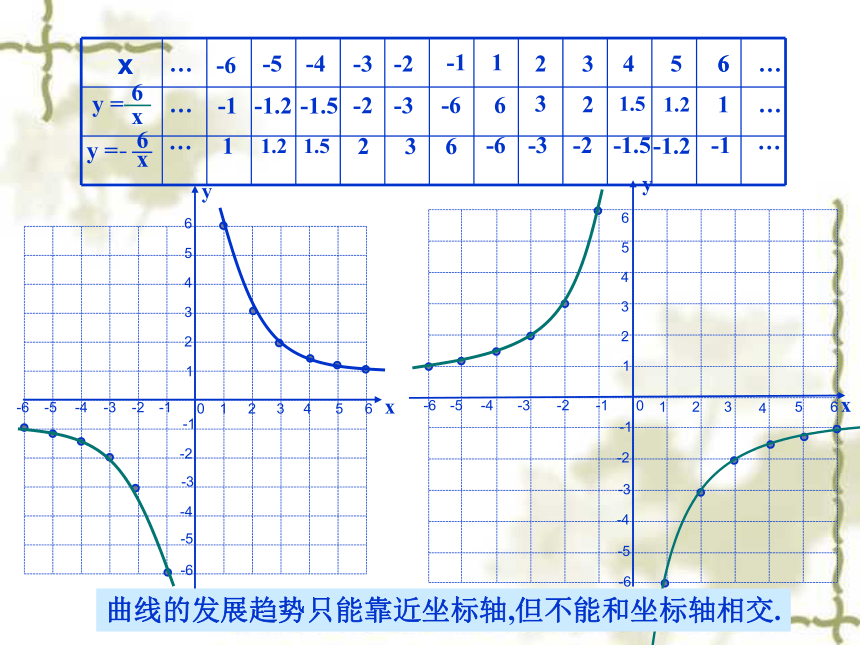
③选整数较好计算和描点。操作一:123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.你认为作反比例函数图象时应注意哪些问题?1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线 ,又可以使图象精确。
2 .描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错。
3.一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接。
4.图像是延伸的,注意不要画成有明确端点。
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
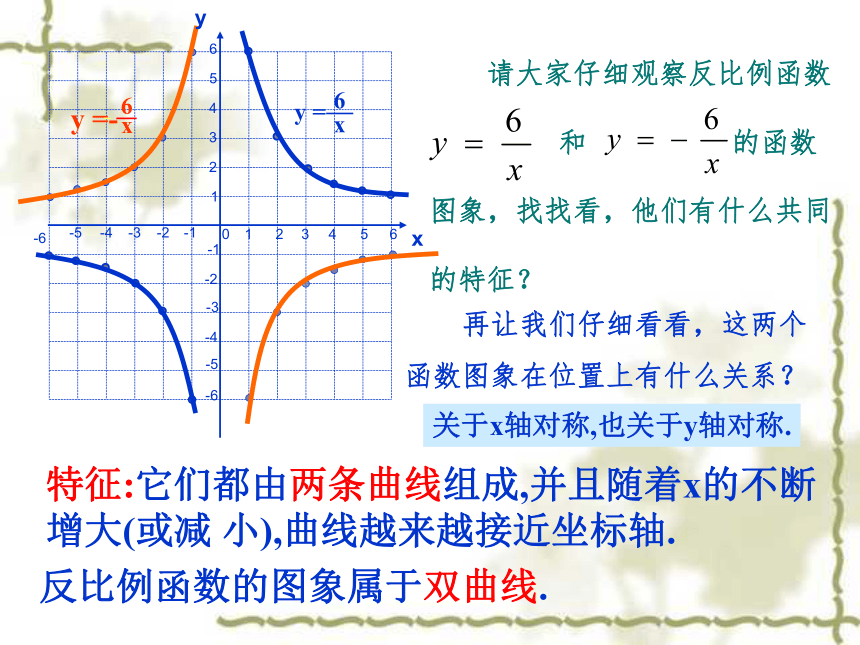
123456-1-3-2-4-51234-1-2-3-40-6-556-6xy 请大家仔细观察反比例函数
和 的函数
图象,找找看,他们有什么共同
的特征? 再让我们仔细看看,这两个
函数图象在位置上有什么关系?特征:它们都由两条曲线组成,并且随着x的不断
增大(或减 小),曲线越来越接近坐标轴.反比例函数的图象属于双曲线.关于x轴对称,也关于y轴对称.123456-1-3-2-4-51234-1-2-3-40-6-556Xy1、这几个函数图象有什么共同点?2、函数图象分别位于哪几个象限?3、y随的x变化有怎样的变化?由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
反比例函数 与 的图象关于x轴对称,也关于y轴对称。反比例函数的图象和性质形状位置增减性图象的发展趋势对称性D活学活用二,四m < 2一、三一、三你学到了什么?回顾:反比例函数的图象和性质
1:形状
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线;
2:位置
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
反比例函数的图象和性质3;性质
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
4:注意事项:
(1)因k≠0,x≠0故y≠0,所以它们都不与坐标轴相交。
(2)画图时注意其美观性(对称性、延伸性):反比例函数的图象既是中心对称图形,又是轴对称图形。它们各自都有一个对称中心两条对称轴;图象分别都是由两支曲线组成的,两个分支都无限趋近但永远不能与x轴和y轴相交。
知识的升华课本46页,第4、5、6题课外探索与交流: 在同一坐标系中,函数 和y=k2x+b的 图像大致如下,则 k1 、k2、b各应满足什么条件?说明理由。 知识的综合运用:祝你成功!再见
① ② ③ ④
⑤ ⑥ ⑦ ⑧
y = 3x-1y = 2x2y = 3x2. 上节课我们学的反比例函数关系式是什么?
自变量x的取值范围是什么?
函数y的取值范围是什么?x≠0 ,y≠0(k ≠0,k是常数)已知一次函数y=kx+b(k≠0)的图象是大家想不想知道:反比例函数 (k≠0)的图象是什么样子呢?让我们一起画个反比例函数的图象看一看。一条直线回顾画出反比例函数 和
的函数图象。
列
表描
点连
线还记得作函数图像的方法吗? 描点法注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。操作一:123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.你认为作反比例函数图象时应注意哪些问题?1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线 ,又可以使图象精确。
2 .描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错。
3.一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接。
4.图像是延伸的,注意不要画成有明确端点。
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
123456-1-3-2-4-51234-1-2-3-40-6-556-6xy 请大家仔细观察反比例函数
和 的函数
图象,找找看,他们有什么共同
的特征? 再让我们仔细看看,这两个
函数图象在位置上有什么关系?特征:它们都由两条曲线组成,并且随着x的不断
增大(或减 小),曲线越来越接近坐标轴.反比例函数的图象属于双曲线.关于x轴对称,也关于y轴对称.123456-1-3-2-4-51234-1-2-3-40-6-556Xy1、这几个函数图象有什么共同点?2、函数图象分别位于哪几个象限?3、y随的x变化有怎样的变化?由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
反比例函数 与 的图象关于x轴对称,也关于y轴对称。反比例函数的图象和性质形状位置增减性图象的发展趋势对称性D活学活用二,四m < 2一、三一、三你学到了什么?回顾:反比例函数的图象和性质
1:形状
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线;
2:位置
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
反比例函数的图象和性质3;性质
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
4:注意事项:
(1)因k≠0,x≠0故y≠0,所以它们都不与坐标轴相交。
(2)画图时注意其美观性(对称性、延伸性):反比例函数的图象既是中心对称图形,又是轴对称图形。它们各自都有一个对称中心两条对称轴;图象分别都是由两支曲线组成的,两个分支都无限趋近但永远不能与x轴和y轴相交。
知识的升华课本46页,第4、5、6题课外探索与交流: 在同一坐标系中,函数 和y=k2x+b的 图像大致如下,则 k1 、k2、b各应满足什么条件?说明理由。 知识的综合运用:祝你成功!再见
