第1章 反比例函数复习课件

课件67张PPT。 信心源自于努力 结合近几年中考试题分析，反比例函数内容的考查主要有以下特点：
1.反比例函数的图象与性质是中考热点之一，特别是反比例函数的增减性、面积问题，都是中考题中经常涉及的知识点.题型以选择题和填空题为主.与其他类型函数的综合题，特别是与一次函数的综合题，通常以解答题的形式出现. 2.反比例函数与物理知识的综合命题，是中考的另一热点，如压力、压强、受力面积的问题，电压、电流、电阻的问题等. 1.反比例函数的图象与性质及其解析式的相关知识是学习本讲的基础,在学习过程中应多分析、多归纳,并结合所给条件画出反比例函数的图象,重点掌握数形结合思想在本讲内容的应用.
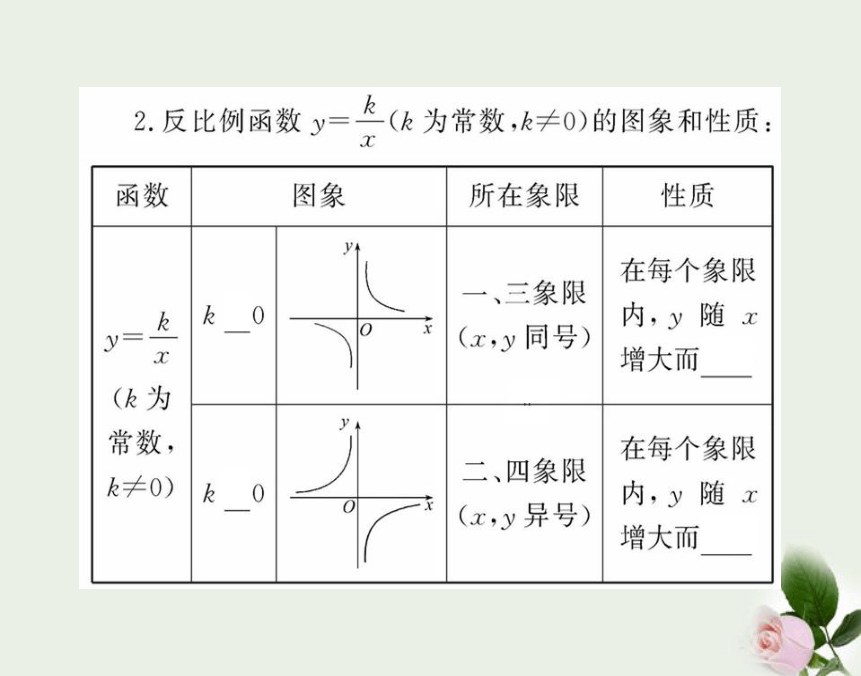
2.反比例函数的解析式的求法及反比例函数与相关知识的融合是中考热点之一,常带有一定的综合性,所以应通过各种形式的题目进行训练.反比例函数的图象与性质1.反比例函数的图象是双曲线,它有两个分支,它们关于原点成中心对称.
2.反比例函数的图象与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远不能与坐标轴相交,在画图时要体现出图象与坐标轴无限贴近的趋势.3.反比例函数的位置和函数的增减性,是由其比例系数k的符号决定的;由反比例函数的图象位置和函数的增减性可以判断k的符号.【例1】(2010·镇江中考)反比例函数 的图象在第二、
四象限，则n的取值范围为_____,A(2,y1),B(3,y2)为图象上两
点，则y1_____y2(用“<”或“>”填空).
【思路点拨】【自主解答】根据题意，得n-1<0,解得n<1;
因为n-1<0,所以在每个象限中，y随x的增大而增大,
又因为2<3,所以y1答案：n<1 <1.(2011·邵阳中考)已知点(1，1)在反比例函数 (k为常
数，k≠0)的图象上，则这个反比例函数的大致图象是( )
【解析】选C.反比例函数的图象是双曲线，又k＝1>0，故图象在一、三象限.2.(2011·连云港中考)关于反比例函数 的图象，下列说
法正确的是( )
(A)必经过点(1,1)
(B)两个分支分布在第二、四象限
(C)两个分支关于x轴成轴对称
(D)两个分支关于原点成中点对称
【解析】选D.反比例函数 的图象在第一、三象限，并且关于原点成中心对称.3.(2011·成都中考)在平面直角坐标系xOy中，已知反比例函
数 (k≠0)满足：当x<0时，y随x的增大而减小.若该反
比例函数的图象与直线 都经过点P，且｜OP｜＝
，则实数k=_____.
【解析】根据题意可得k>0.设P点的坐标为 列方
程得
解得
答案： 4.(2010·常德中考)已知图中的曲线
是反比例函数 (m为常数)图象
的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x
的图象在第一象限的交点为A(2，n)，求点A的坐标及反比例函数的解析式.【解析】(1)∵这个反比例函数的图象分布在第一、第三象限，
∴m-5>0，解得m>5.
(2)∵点A(2,n)在正比例函数y=2x的图象上，
∴n=2×2=4,则A点的坐标为(2,4).
又∵点A在反比例函数 的图象上，
∴ ，即m-5=8.
∴反比例函数的解析式为反比例函数解析式的确定用待定系数法求反比例函数解析式的一般步骤:
(1)设所求的反比例函数解析式为 (k≠0);
(2)根据已知条件(自变量与函数的对应值)列出含k的方程;
(3)解方程得待定系数k的值;
(4)把k值代入函数解析式 .【例2】(2011·菏泽中考)已知一次函数y=x+2与反比例函数 ，其中一次函数y=x+2的图象经过点P(k,5).
(1)试确定反比例函数的解析式；
(2)若点Q是上述一次函数与反比例函数图象在第三象限的交点，求点Q的坐标.
【思路点拨】(1)由一次函数y=x+2经过点P(k，5)求k的值.
(2)解由一次函数与反比例函数解析式组成的方程组，由点Q在第三象限确定点Q的坐标.【自主解答】(1)因一次函数y=x+2的图象经过点P(k,5)，
所以得5=k+2，解得k=3,
所以反比例函数的解析式为
(2)联立一次函数与反比例函数解析式，得方程组
解得 或
故第三象限的交点Q的坐标为(-3，-1).5.(2010·潍坊中考)若正比例函数y＝2kx与反比例函数
(k≠0)的图象交于点A(m，1)，则k的值是( )
(A) (B)
(C) (D)
【解析】选B.由题意,得 ,解得6.(2011·福州中考)如图，△OPQ是边
长为2的等边三角形，若反比例函数的
图象过点P，则它的解析式是_____.
【解析】过点P作PD⊥OQ于点D.则∠OPD＝30°，
∴OD＝1，PD＝ ，∴点P的坐标为(1， ).
设过点P的反比例函数解析式是 ，则
∴函数解析式为
答案： 7.(2011·綦江中考)如图，已知
A(4,a)，B(-2,-4)是一次函数
y=kx+b的图象和反比例函数
的图象的交点.
(1)求反比例函数和一次函数的解
析式；
(2)求△AOB的面积.【解析】(1)因为点B(-2，-4)在反比例函数的图象上，所以m=(-2)×(-4)=8.当x=4时，
可得方程组 ，解得k=1,b=-2.
所以反比例函数和一次函数的解析式分别为 和y=x-2.
(2)设直线AB与x轴的交点为C，可得C点的坐标为(2,0)，所以
反比例函数的实际应用1.利用反比例函数的知识,正确解释日常生活中的特殊事件;
2.能通过实例构建反比例函数模型,从而解决问题;
3.根据题意或图象,列出关系式,并确定自变量的取值范围.【例3】(2010·湛江中考)病人按规
定的剂量服用某种药物，测得服药
后2小时，每毫升血液中的含量达到
最大值为4毫克.已知服药后，2小时
前每毫升血液中的含量y(毫克)与时间x(小时)成正比例；2小时后y与x成反比例(如图所示).根据以上信息解答下列问题：(1)求当0≤x≤2时，y与x的函数解析式；
(2)求当x>2时，y与x的函数解析式;
(3)若每毫升血液中的含量不低于2毫克时的治疗有效，则服药一次，治疗疾病的有效时间是多长？【思路点拨】
【自主解答】(1)当0≤x≤2时，设函数解析式为y=k1x,由题意得4=2k1,解得k1=2,
∴当0≤x≤2时，函数解析式为y=2x.(2)当x>2时,设函数解析式为 ,由题意得 解得
k2=8,
∴当x>2时，函数解析式为
(3)把y=2代入y=2x中，得x=1,
把y=2代入 中，得x=4,∴4-1=3.
答：服药一次，治疗疾病的有效时间是3小时.8.(2010·菏泽中考)某种气球内充
满了一定质量的气体，当温度不变
时，气球内气体的气压P(kPa)是气
球体积V的反比例函数，其图象如图
所示，当气球内的气压大于120 kPa时，气球将爆炸，为了安全，气球的体积应该( )
(A)不大于 (B)小于
(C)不小于 (D)小于【解析】选C.由题意,得120V=1.6×60，所以
又因为，当气球内的气压大于120 kPa时，气球将爆炸,
所以为了安全，气球的体积应该不小于9.(2011·南充中考)小明乘车从南充到成都，行车的平均速度v(km/h)和行车时间t(h)之间的函数图象是( )
【解析】选B.小明乘车从南充到成都，路程一定，即行车的平均速度v(km/h)和行车时间t(h)的乘积一定.所以行车的平均速度v(km/h)和行车时间t(h)成反比例函数关系，而行车的平均速度v和行车时间t均不为负数，故选B.10.(2010·綦江中考)有一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度ρ(单位：kg/m3)是体积V(单位：m3)的反比例函数，它的图象如图所示，当V＝2m3时，气体的密度是_____kg/m3.【解析】由题意可得函数解析式为： 当V=2时，ρ=4.
答案：4反比例函数的比例系数k的几何意义 反比例函数 (k≠0)中比例系数k的几何意义:
(1)过双曲线 (k≠0)上任意一点作x轴、y轴的垂线，所
得矩形OAPB的面积为|k|.
(2)过双曲线 (k≠0)上任意一点作一坐标轴的垂线，连
接该点和原点，所得三角形OCQ的面积为【例】(2010·昆明中考)
如图，点A(x1，y1)、
B(x2，y2)都在双曲
线 (x>0)上，且
x2-x1=4，y1-y2=2；
分别过点A、B向x轴、y轴作垂线段，垂足分别为C、D、E、F，AC与BF相交于G点，四边形FOCG的面积为2，五边形AEODB的面积为14，那么双曲线的解析式为_____.【思路点拨】 【自主解答】因为x2-x1=4，y1-y2=2，
所以GB=4，AG=2，△AGB的面积=
因为四边形FOCG的面积为2，五边形AEODB的面积为14,
所以四边形AEFG的面积=四边形CDBG的面积=4，
四边形AEOC的面积=6，
所以k=6，双曲线的解析式为 (x>0).
答案： (x>0)1.(2011·黄冈中考)如图，点A在双
曲线 上，AB⊥x轴于B，且△AOB
的面积S△AOB=2，则k=_____.
【解析】∵S△AOB=2,即 ，
∴AB·OB=4,
∵图象位于二、四象限，∴k=-4.
答案：-42.(2010·济宁中考)如图，正比例函
数 的图象与反比例函数
(k≠0)在第一象限的图象交于A点，
过A点作x轴的垂线，垂足为M，已知
△OAM的面积为1.
(1)求反比例函数的解析式；
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合)，且B点的横坐标为1，在x轴上求一点P，使PA+PB最小.【解析】(1)设A点的坐标为(a，b)，
则
∵
∴反比例函数的解析式为
(2)由 得 或
又∵点A在第一象限内，∴A为(2，1).
设A点关于x轴的对称点为C，则C点的坐标为(2，-1).
令直线BC的解析式为y=mx+n.
∵B为(1，2)，∴ ,∴
∴BC的解析式为y=-3x+5.
当y=0时，x= ，∴P点为( ，0).1.(2010·青岛中考)函数y=ax-a与 (a≠0)在同一直角坐
标系中的图象可能是( )【解析】选D.可分类考虑：当a>0时，函数y=ax-a的图象在一、
三、四象限， 的图象在一、三象限；当a<0时，函数
y=ax-a的图象在一、二、四象限, 的图象在二、四象限;
只有选项D符合题意,故选D.2.(2009·娄底中考)数学课外兴趣小组的同学每人制作一个面积为200 cm2的矩形学具进行展示.设矩形的宽为x cm,长
为y cm，那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( )【解析】选A.∵矩形面积为：S矩=x·y.
∴ (x>0),根据图象可知，只有A项符合.3.(2010·兰州中考)已知点(-1,y1)，(2,y2)，(3,y3)在反比例函数 的图象上.下列结论中正确的是( )
(A)y1>y2>y3 (B)y1>y3>y2
(C)y3>y1>y2 (D)y2>y3>y1
【解析】选B.根据题意可知，反比例函
数 的图象在第二、四象限，其
大致图象如图所示，在图象上标出点
(-1,y1)，(2,y2)，(3,y3)，显然有y1>y3>y2.4.(2010·衡阳中考)如图，已知双曲线
(k>0)经过直角三角形OAB斜边OB的
中点D，与直角边AB相交于点C.若△OBC
的面积为3，则k＝_____.【解析】由点D、C都在双曲线 (k>0)，得S△ODE =S△OCA,由题意易得△ODE∽△OBA,所以
,解得S△ODE=1，而 ,所以k=xy=2.
答案：25.(2010·衢州中考)若点(4，m)在反比例函数 (x≠0)的图象上，则m的值是_____.
【解析】将(4，m)代入 ，得
答案：26.(2010·郴州中考)已知：
如图，双曲线 的图象
经过A(1,2)、B(2,b)两点.
(1)求双曲线的解析式；
(2)试比较b与2的大小.【解析】(1)因为点A(1，2)在函数 上,所以 ，即k=2，
所以双曲线的解析式为
(2)由函数 的性质可得在第一象限y随x的增大而减小，因为2>1,所以b<2.
(注：还可用点在函数图象上求出b的值，从而比较b与2的大小)7.(2010·巴中中考)一次函数y=kx+b
与反比例函数 的图象交于点
A(2，1)，B(-1，n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)求△AOB的面积.【解析】(1)把A(2，1)代入 ，得m=2，所以反比例函数的解析式为
(2)因为点B(-1，n)也在反比例函数的图象上，所以n=-2，把A、B两点的坐标代入y=kx+b得：
，解得
所以一次函数的解析式为y=x-1.(3)如图，设AB交y轴于点C，则C点的坐标为(0，-1),所以OC=1.分别过A、B作y轴的垂线，垂足为E、F，可知AE=2,BF=1.
所以S△AOB=S△AOC+S△BOC
=Thank you!诲人不倦悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考, 去发现，去总结。教师寄语再见 祝你成功！