湘教版数学九年级上册第1章 反比例函数 复习课件 29张PPt
文档属性
| 名称 | 湘教版数学九年级上册第1章 反比例函数 复习课件 29张PPt |

|
|
| 格式 | zip | ||
| 文件大小 | 809.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-01 00:00:00 | ||
图片预览





文档简介
课件29张PPT。反比例函数复习课对于一次函数 、反比例函数
我们是如何学习的? ①先研究一次函数的定义
②接着研究一次函数图象的画法
③再研究一次函数的性质
④最后研究一次函数的应用想一想(k ≠0)反比例函数三种等价形式:一、反比例函数的定义:②⑤用(1)⑥为什么不是?A用(2)
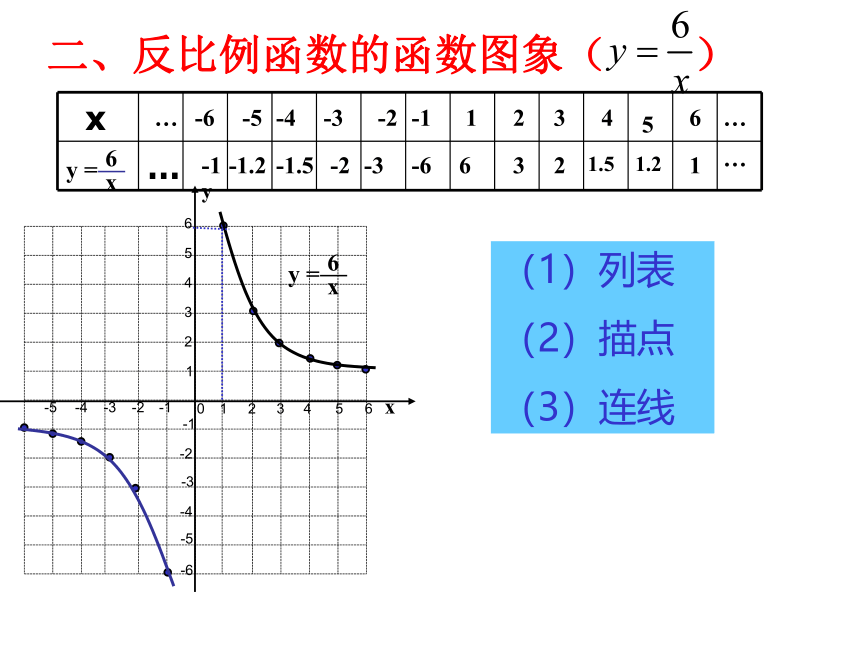
D用(3)123456-1-3-2-4-51234-1-2-3-40-6-556xy16233241.551.216-1-6-2-3-3-1.5-2-4-5-1.2-6-1………二、反比例函数的函数图象( )(1)列表
(2)描点
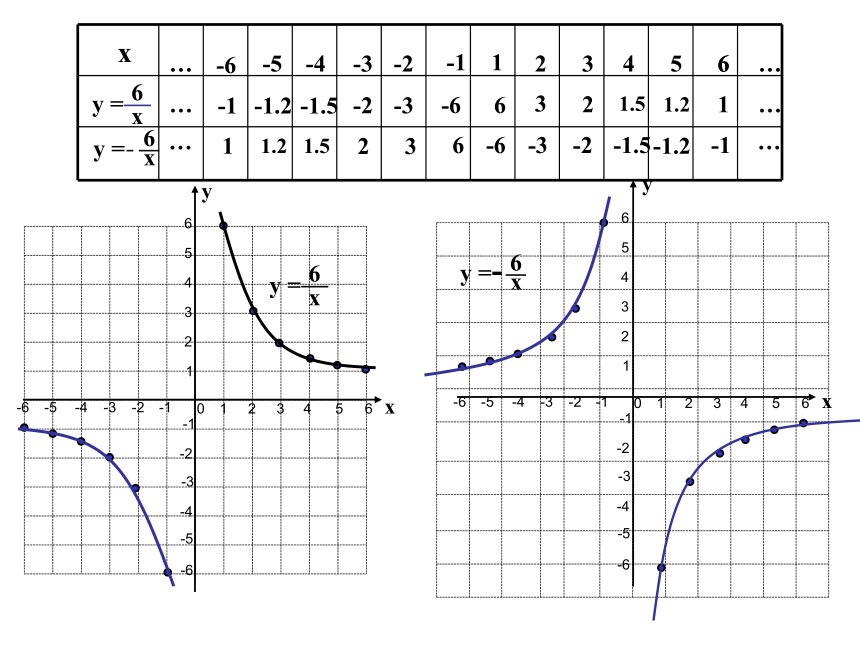
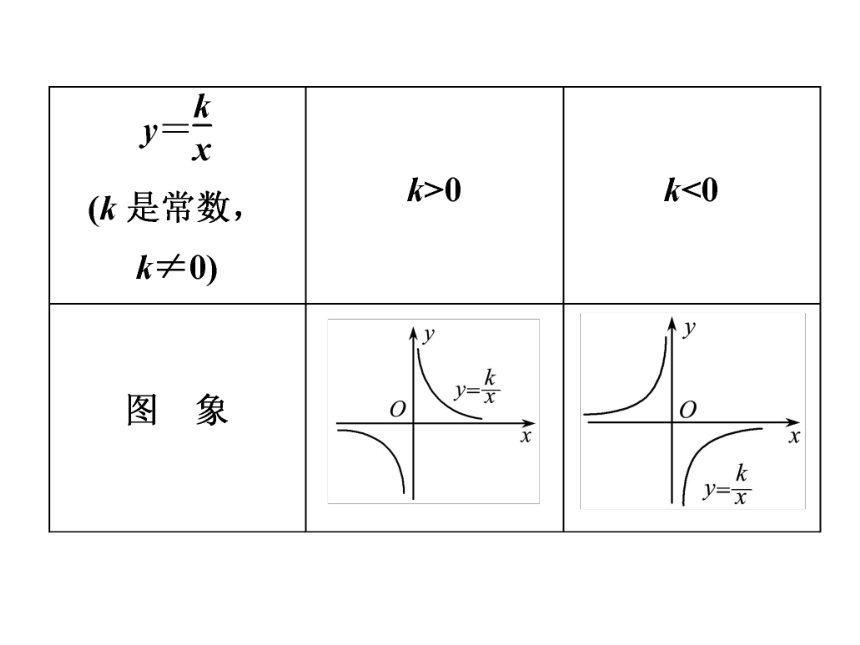
(3)连线123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……2.你能回顾总结一下反比例函数的图象性质特征吗? 与同伴进行交流. 图象是双曲线 当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内 当k>0时,在每一象限内,y随x的增大而减小
当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远
不会与坐标轴相交双曲线是中心对称图形.又是轴对称图形,y=x与 y=-x是它的两条对称轴,原点是它的对称中心。形状
位置
增减性
变化趋势
对称性形 状位 置增减性变化趋势对称性 你同意他的观点吗?
试说明理由变式练习 函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的
大小关系是_______________;y3< y1< y2 观察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-10变式练习例:若正比例函数 的图象与反比例函数
的图象的一个交点是 ,则它们的另一交点是_____ 三、k 值与面积问题在反比例函数 图象上,任意取一点向两坐标轴作垂线段,与两坐标轴所围成的矩形的面积为|k|.面积为矩形,则它的面积为_
__
解析:延长 BA 与 y 轴相交于点E,则矩形OC BE 的面积为3,同理矩形 ODAE 的面积为 1,所以矩形 ABC D 的面积为2.2-4变式练习四、反比例函数与一次函数的综合应用1.要确定反比例函数的解析式只需知道或求出一个点的坐标;要确定一次函数的解析式一般要知道或求出两个点的坐标;
2.解决两种函数的综合问题,要抓住关键点——交点.求它们的交点A、B 的坐标时,可以根据函数与方程的关系,将两个函数关系式联立方程组求解即可.
3.比较两个函数值的大小,利用数形结合,从交点出发,图象在上的函数值大,反之,函数值小;注意反比例函数的断点——x≠0(取值范围不为零).
2、如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围
是( ).A、x<-1 B、x>2
C、-1<x<0或x>2 D、x<-1或0<x<2D1.(2012 广州)如图 ,正比例函数 y1=k1x 和反y2,则 x 的取值范围是()DA.x<-1 或 x>1
B.x<-1 或 0<x<1
C.-1<x<0 或 0<x<1
D.-1<x<0 或 x>1变式练习1、已知反比例函数y= 的图象在第一、三象限, 则一次函数y= -kx+4经过第 象限一、二、四
变式练习(2014遂宁10分)已知:如图,反比例函数
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于
反比例函数值的自变量x的
取值范围.变式练习解(1) ∵A(1,4)在y= ,y=x+b上,
∴4= , 4=1+b, ∴k=4,b=3,
∴一次函数的解析式为y=x+3,反比例函数的解析式为y=4x;(2)∵点B在y=x+3上,∴n=-4+3 =-1,
∴点B的坐标为(-4,-1),
设y=x+3与y轴交于点C(0,y),
令x=0,则y=3,
∴点C的坐标为(0,3),∴OC=3,
如解图,过点A、B分别作y轴垂线
AE、BF,交y轴于E、F点,
由A(1,4),B(-4,-1)
可知AE=1,BF=4,∴△OAB的面积为 (3) x的取值范围是-41五、实际问题与反比例函数1. 病人按规定的剂量服用某种药物,测得服药后
2小时,每毫升血液中的含药量达到最大值为 4 毫克.
已知服药后,2 小时前每毫升血液中的含药量 y(单位:
毫克)与时间 x(单位:小时)成正比例;2 小时后 y 与 x
成反比例(如图 26-7) .根据以上信息解答下列问题:
(1)求当 0≤x≤2 时,y 与 x 的函数关系式;
(2)求当 x>2 时,y 与 x 的函数关系式;(3)若每毫升血液中的含药量
不低于 2毫克时治疗有效,
则服药一次,治疗疾病的
有效时间是多长?
解:(1)当 0≤x≤2 时,y 与 x 成正比例函数关系.
设 y=kx,由于点(2,4)在直线上,
所以 4=2k,k=2,即 y=2x.
(2)当 x>2 时,y 与 x 成反比例函数关系.
设 y=k/x,由于点(2,4)反比例函数的图象上,
所以 k=2×4=8,即 y=8/x.
(3)当 0≤x≤2 时,含药量不低于 2 毫克,
即 2x≥2,x≥1.即服药 1 小时后;
当 x>2 时,含药量不低于 2 毫克,所以服药一次,治疗疾病的有效时间是
1+2=3(小时).忽略自变量的取值范围. 已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).C
我们是如何学习的? ①先研究一次函数的定义
②接着研究一次函数图象的画法
③再研究一次函数的性质
④最后研究一次函数的应用想一想(k ≠0)反比例函数三种等价形式:一、反比例函数的定义:②⑤用(1)⑥为什么不是?A用(2)
D用(3)123456-1-3-2-4-51234-1-2-3-40-6-556xy16233241.551.216-1-6-2-3-3-1.5-2-4-5-1.2-6-1………二、反比例函数的函数图象( )(1)列表
(2)描点
(3)连线123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……2.你能回顾总结一下反比例函数的图象性质特征吗? 与同伴进行交流. 图象是双曲线 当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内 当k>0时,在每一象限内,y随x的增大而减小
当k<0时,在每一象限内,y随x的增大而增大
双曲线无限接近于x、y轴,但永远
不会与坐标轴相交双曲线是中心对称图形.又是轴对称图形,y=x与 y=-x是它的两条对称轴,原点是它的对称中心。形状
位置
增减性
变化趋势
对称性形 状位 置增减性变化趋势对称性 你同意他的观点吗?
试说明理由变式练习 函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的
大小关系是_______________;y3< y1< y2 观察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
__
解析:延长 BA 与 y 轴相交于点E,则矩形OC BE 的面积为3,同理矩形 ODAE 的面积为 1,所以矩形 ABC D 的面积为2.2-4变式练习四、反比例函数与一次函数的综合应用1.要确定反比例函数的解析式只需知道或求出一个点的坐标;要确定一次函数的解析式一般要知道或求出两个点的坐标;
2.解决两种函数的综合问题,要抓住关键点——交点.求它们的交点A、B 的坐标时,可以根据函数与方程的关系,将两个函数关系式联立方程组求解即可.
3.比较两个函数值的大小,利用数形结合,从交点出发,图象在上的函数值大,反之,函数值小;注意反比例函数的断点——x≠0(取值范围不为零).
2、如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围
是( ).A、x<-1 B、x>2
C、-1<x<0或x>2 D、x<-1或0<x<2D1.(2012 广州)如图 ,正比例函数 y1=k1x 和反y2,则 x 的取值范围是()DA.x<-1 或 x>1
B.x<-1 或 0<x<1
C.-1<x<0 或 0<x<1
D.-1<x<0 或 x>1变式练习1、已知反比例函数y= 的图象在第一、三象限, 则一次函数y= -kx+4经过第 象限一、二、四
变式练习(2014遂宁10分)已知:如图,反比例函数
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于
反比例函数值的自变量x的
取值范围.变式练习解(1) ∵A(1,4)在y= ,y=x+b上,
∴4= , 4=1+b, ∴k=4,b=3,
∴一次函数的解析式为y=x+3,反比例函数的解析式为y=4x;(2)∵点B在y=x+3上,∴n=-4+3 =-1,
∴点B的坐标为(-4,-1),
设y=x+3与y轴交于点C(0,y),
令x=0,则y=3,
∴点C的坐标为(0,3),∴OC=3,
如解图,过点A、B分别作y轴垂线
AE、BF,交y轴于E、F点,
由A(1,4),B(-4,-1)
可知AE=1,BF=4,∴△OAB的面积为 (3) x的取值范围是-4
2小时,每毫升血液中的含药量达到最大值为 4 毫克.
已知服药后,2 小时前每毫升血液中的含药量 y(单位:
毫克)与时间 x(单位:小时)成正比例;2 小时后 y 与 x
成反比例(如图 26-7) .根据以上信息解答下列问题:
(1)求当 0≤x≤2 时,y 与 x 的函数关系式;
(2)求当 x>2 时,y 与 x 的函数关系式;(3)若每毫升血液中的含药量
不低于 2毫克时治疗有效,
则服药一次,治疗疾病的
有效时间是多长?
解:(1)当 0≤x≤2 时,y 与 x 成正比例函数关系.
设 y=kx,由于点(2,4)在直线上,
所以 4=2k,k=2,即 y=2x.
(2)当 x>2 时,y 与 x 成反比例函数关系.
设 y=k/x,由于点(2,4)反比例函数的图象上,
所以 k=2×4=8,即 y=8/x.
(3)当 0≤x≤2 时,含药量不低于 2 毫克,
即 2x≥2,x≥1.即服药 1 小时后;
当 x>2 时,含药量不低于 2 毫克,所以服药一次,治疗疾病的有效时间是
1+2=3(小时).忽略自变量的取值范围. 已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).C
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
