3.5 相似三角形应用 课件3

课件14张PPT。相似三角形的性质及其应用
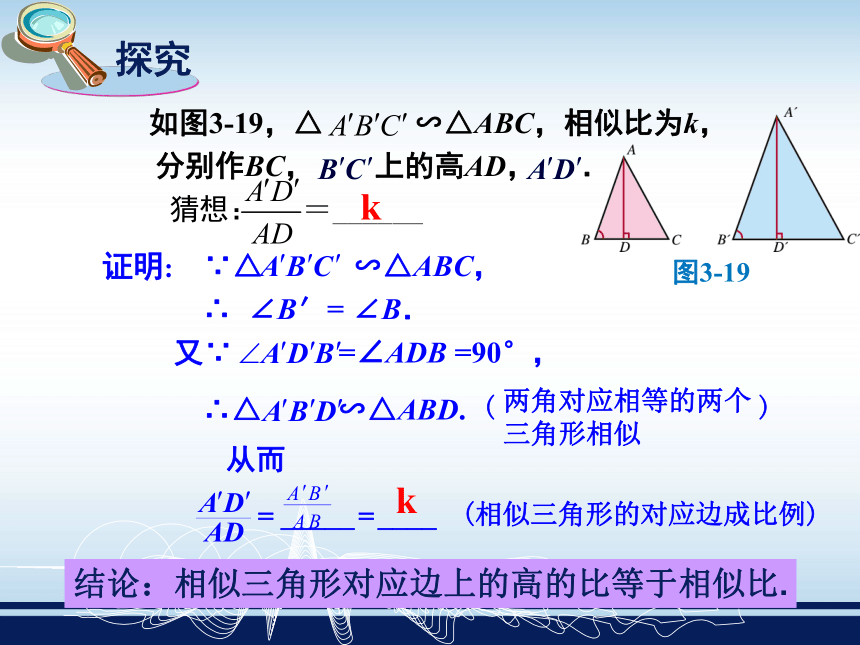
1.相似三角形的基本性质是什么？2.如何判定两三角形相似？ 如图3-19，△ ∽△ABC，相似比为k，
分别作BC， 上的高AD， ．
猜想：∴ ∠B′= ∠B．又∵ =∠ADB =90°，∴△ ∽△ABD. 图3-19结论：相似三角形对应边上的高的比等于相似比.k两角对应相等的两个
三角形相似k( ) 若△ ∽△ABC，相似比为k，
那么它们的周长比是多少？面积比是多少？图3-19∴解：∴ 从而从而= k 若△ ∽△ABC，相似比为k，
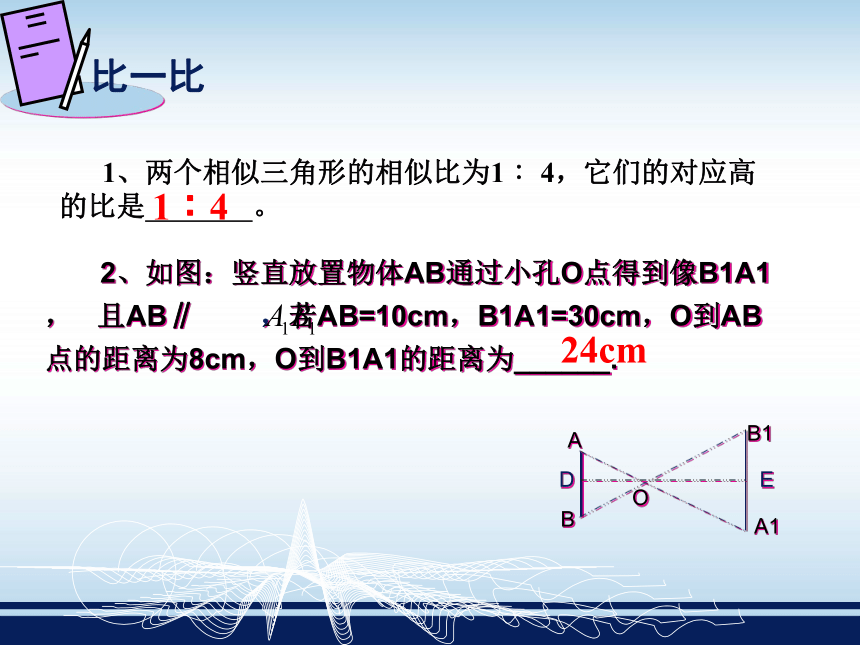
那么它们的周长比是多少？面积比是多少？图3-19解： ∵ △ ∽ △ ABC从而=k∴(等比性质)= = k×k=k2相似三角形对应边上的高的比等于相似比.相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方. 2、如图：竖直放置物体AB通过小孔O点得到像B1A1， 且AB∥ ，若AB=10cm，B1A1=30cm，O到AB点的距离为8cm，O到B1A1的距离为______.ABOB1A1DE24cm 1、两个相似三角形的相似比为1 ∶4，它们的对应高的比是 。1︰43.在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积各发生什么变化?三角形的边长,周长放大为10倍，
三角形的面积放大为100倍6、若△ ABC ∽△A1B1C1 ，且S△ ABC：S△ A1B1C1=4:9,
AB=4cm， 则A1B1 =_____。6cm5、若△ ABC ∽△A1B1C1 ，△ABC的周长为13cm，AB=4cm，,A1B1 =8cm， 则△ A1B1C1的周长为_____。26cm4、两个相似三角形的对应边上的高的比为1 ∶3，它们的周长比是 ，面积比是 。 1:31:9 如图， △ABC是一张锐角三角形硬纸片，AD是边BC上的高，BC＝40cm，AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2 倍的矩形EFGH，使它的一边EF在BC上，定点G、H分别在AC、 AB上，AD与HG的交点为M. 求矩形的面积。解得，x=12 所以EFGH的面积为12×24=288(c㎡).设HE=xcm ,则HG=2xcm,AM=(30- x)cm解： ∵ HEFG是矩形 ∴HG//BC∴△AHG∽△ABC即 HE=12cm ,HG=24c 答： 矩形的面积为288c㎡ 如图， △ABC是一张锐角三角形硬纸片，AD是边BC上的高，BC＝40cm，AD=30cm,从这张硬纸片上剪下一个矩形EFGH，使它的一边EF在BC上，点G、H分别在AC、 AB上，AD与HG的交点为M. 设HE=Xcm.（1）用X的代数式表示HG的长。
（2）用X的代数式表示矩形HEFG的面积。
＊（3）能否剪出最大面积的矩形？若能，X应取多大？
最大面积为多少？
你今天有什么收获？祝 你 成 功 ！2.（书81）如图， △ABC是一张锐角三角形硬纸片，AD是边BC上
的高，BC＝30cm,AD=20cm,从这张硬纸片上剪下一个正方形EFGH,
使它的一边EF在BC上，定点G、H分别在AC、 AB上，AD与HG的交
点为M. 求这个正方形的边长。 你能用我们今天所学的方法（猜想，论证）探索相似
三角形对应中线，对应角平分线的比与相似比的关系 吗？
谢谢各位领导 、专家和老师的亲临指导！
谢谢各位同学的合作！