3.5 相似三角形应用 课件4

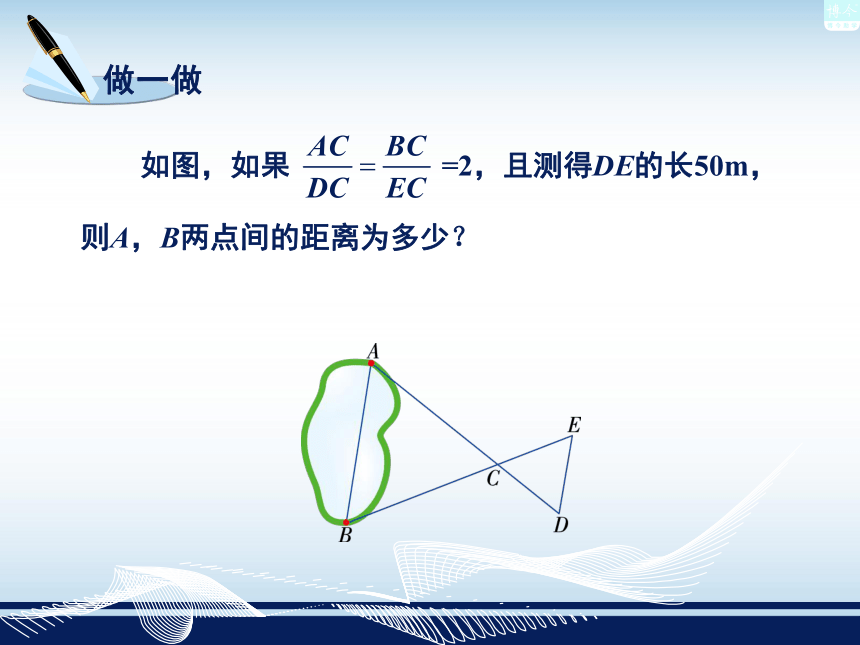
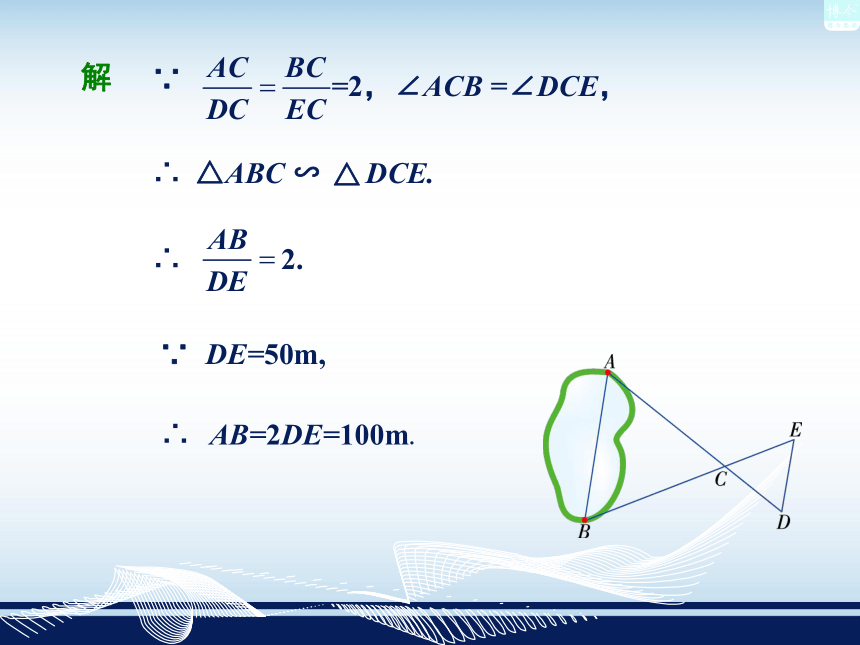
课件15张PPT。相似三角形的应用3.5 如图，A，B两点分别位于一个池塘的两端，小张想测量出A，B间的距离，但由于受条件限制无法直接测量，你能帮他想出一个可行的测量办法吗？举
例例
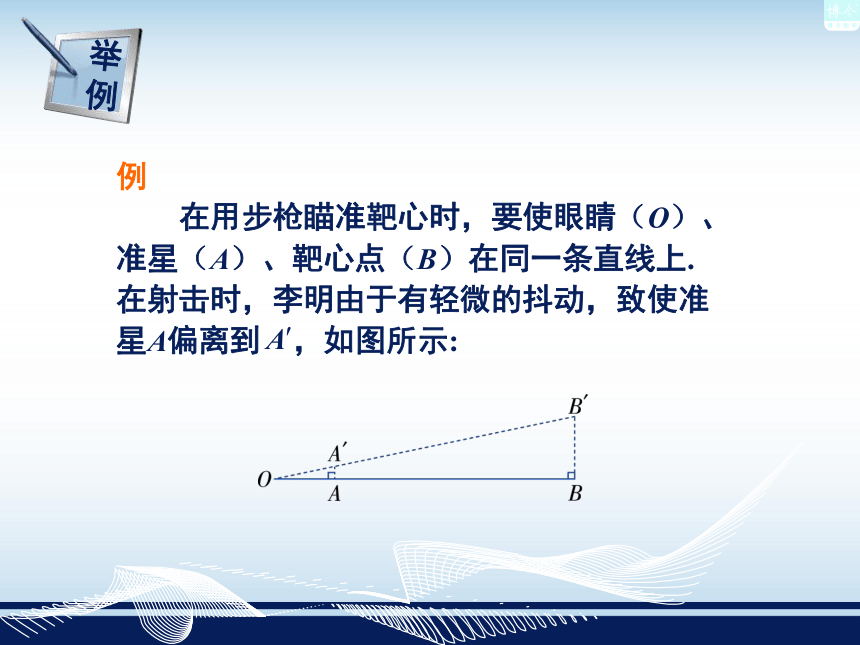
在用步枪瞄准靶心时，要使眼睛（O）、 准星（A）、靶心点（B）在同一条直线上.
在射击时，李明由于有轻微的抖动，致使准
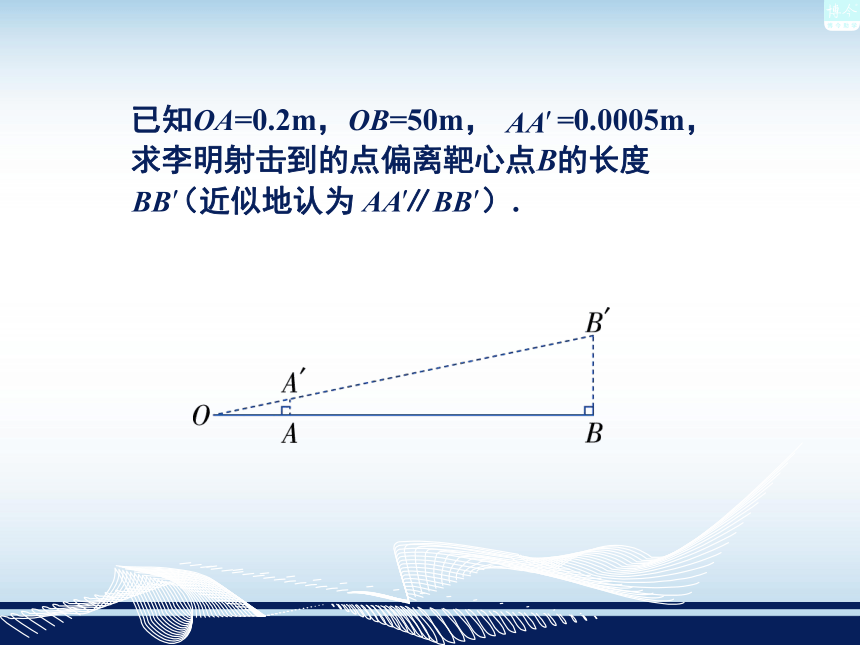
星A偏离到 ，如图所示:已知OA=0.2m，OB=50m， =0.0005m，
求李明射击到的点偏离靶心点B的长度
（近似地认为 ∥ ）.∴∵ OA=0.2m，OB=50m， =0.0005m，∴ = 0.125m.答：李明射击到的点 偏离靶心点B的长度 为0.125m.1.如图，某路口栏杆的短臂长为1m，长臂长为6m.
当短臂端点下降0.5m时，长臂端点升高多少米？由图易知 解Rt△OAB ∽Rt△所以有所以2.如图，小红同学用自制的直角三角形纸板DEF
量树的高度AB，她调整自己的位置，设法使斜
边DF保持水平，并且边DE与点B在同一直线上.
已知纸板的两条直角边DE=80cm，EF=40cm，
测得AC=1.5m，CD=8m，求树高AB.如图所示：∵ O为AB的中点，OC⊥AD，BD⊥AD，∴ OC∥BD，∴ OC是△ABD的中位线，∴ h1=2OC，同理，当将横板AB换成横板A′B′，且A′B′=2AB，O
仍为A′B′的中点，设B′点的最大高度为h2，则h2=2OC，∴ h1=h2．故应选择C.解结 束