青岛版(六三制)数学八年级上册 5.3几何证明举例(第二课时) 课件(共17张PPT)
文档属性
| 名称 | 青岛版(六三制)数学八年级上册 5.3几何证明举例(第二课时) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-24 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第二课时
几何证明举例
一、预习诊断
1.等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
2.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
3.等腰三角形一个角为110°,它的另外两个角为_______ 。等腰三角形一个角为80°,它的另外两个角是_______。
1.进一步掌握证明的基本步骤和书写格式。
2.能用“公理”和“已经证明的定理”为依据,证明等腰三角形的性质定理和判定定理。
教学目标
回顾与思考
1.什么叫等腰三角形?
2.根据本册第二章的学习你知道等腰三角形的哪些性质?
3.这些性质你是怎样得到的?这些性质都是真命题吗?你能用逻辑推理的方法对它们进行证明吗?
二、精讲点拨
证明性质定理1:等腰三角形的两个底角相等
(简称:等边对等角)
已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C
分析:常见辅助线做法(1)作底边上的高
(2)作顶角的平分线 (3)作底边上的中线
通过添加辅助线把三角形ABC分成两个
全等的三角形,只要证得被分成的两个
三角形全等即可得∠B=∠C
A
B
C
D
C
B
A
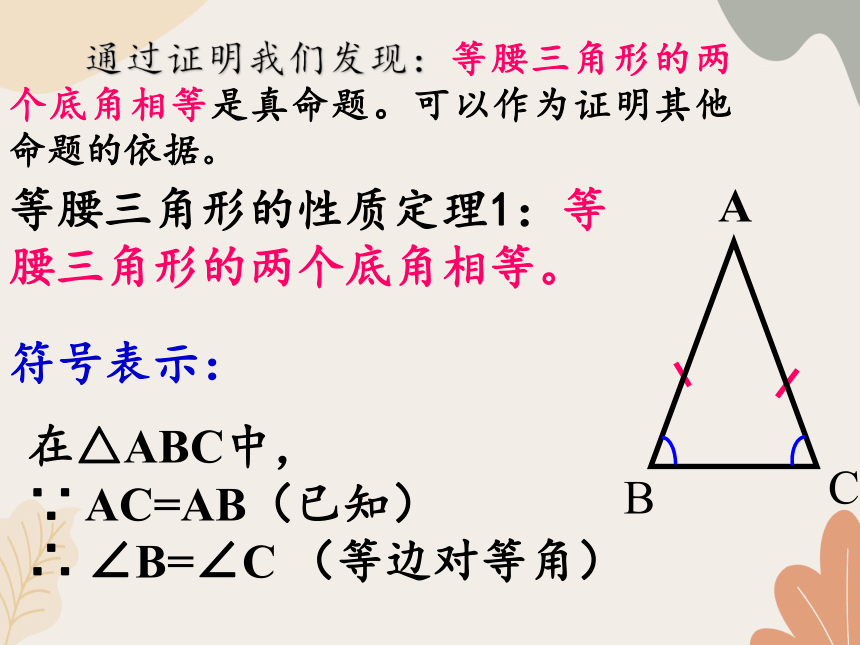
等腰三角形的性质定理1:等腰三角形的两个底角相等。
在△ABC中,
∵ AC=AB(已知)
∴ ∠B=∠C (等边对等角)
通过证明我们发现:等腰三角形的两个底角相等是真命题。可以作为证明其他命题的依据。
符号表示:
交流与发现
根据以上证明,我们还可以得到结论:等腰三角形底边上的高平分底边并且平分顶角。即得到∠BAD=∠CAD与BD=CD,于是得:
性质定理2: 等腰三角形的顶角平分线、底边上的中线、底上的高互相重合(简称“三线合一”)。
A
C
B
D
A
C
B
D
∥
∥
(2)∵AB=AC
图⑵
图⑶
∟
1
2
∥
A
C
B
D
1
2
性质定理2:符号语言的应用
∟
(1)∵AB=AC,
∴AD⊥BC,
BD=CD。
∠1=∠2,
∴AD⊥BC
BD=CD,
∠1=∠2。
(3)∵AB=AC,
AD⊥BC
∴BD=CD,
∠1=∠2。
图⑴
∟
∥
1
2
交流与发现
你能写出“性质定理1:等腰三角形的两个底角相等”的逆命题吗?如何证明这个逆命题是正确的?
如果一个三角形的两个角相等,那么这两个角所对的边也相等。(简称等角对等边)
已知:如图,在△ABC中,∠B=∠C。
求证: AB=AC
分析:是不是仍然可以做辅助线将原三角形
分成两个全等的三角形呢?试试看。
A
B
C
D
等腰三角形的判定定理:
如果一个三角形的两个角相等,那么这两个角所对的边也相等。(简称等角对等边)
C
B
A
符号表示:
在△ABC中,
∵∠B=∠C (已知)
∴ AC=AB(等角对等边)
利用等腰三角形的性质定理和判定定理证明:
学以致用
1.等边三角形的每个内角都是60°
2.三个角都相等的三角形是等边三 角形。
如果一个三角形的每个内角都等于60°,那么这个三角形是等边三角形。
2.当等腰三角形的顶角是60°时
这个逆命题是真命题
1.当等腰三角形的一个底角等于60°角时
思考:“等边三角形的每个内角都等于60°”的逆命题是什么?这个逆命题是真命题吗?
有一个角是60°的等腰三角形是等边三角形吗?
交流与发现
例2:已知:在△ABC中,AB=AC,D是AB上的一点,DE ⊥BC,交BC于点E,交CA的延长线于点F。
求证:AD=AF
分析:从已知出发先由已知AB=AC利用“等边对等角”推得∠B=∠C ,再由等角的余角相等推得∠BDE=∠F,进而得到∠ADF=∠F,最后根据“等角对等边”推出AD=AF。
练一练
1.已知,如图D是△ ABC内的一点,且DB=DC,BD平分∠ABC,CD平分∠ACB,
求证:AB=AC
C
B
A
D
2.在△ABC中,∠ABC、∠ACB的平分线相交
于点O,过点O作DE∥BC,分别交AB、AC于
点D、E。
请说明DE=BD+EC。
3.如图,△ABC是等边三角形,
BD是AC边上的高,延长BC至E,
使CE=CD。连接DE。
(1)∠E等于多少度?
(2)△DBE是什么三角形?
为什么?
三、系统总结
1.等腰三角形的判定方法有下列两种:
①定义②判定定理
2.等腰三角形的判定定理与性质定理的区别
条件和结论刚好相反
3.运用等腰三角形的判定定理时,应注意
在同一个三角形中
谢 谢
第二课时
几何证明举例
一、预习诊断
1.等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;
2.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是 。
3.等腰三角形一个角为110°,它的另外两个角为_______ 。等腰三角形一个角为80°,它的另外两个角是_______。
1.进一步掌握证明的基本步骤和书写格式。
2.能用“公理”和“已经证明的定理”为依据,证明等腰三角形的性质定理和判定定理。
教学目标
回顾与思考
1.什么叫等腰三角形?
2.根据本册第二章的学习你知道等腰三角形的哪些性质?
3.这些性质你是怎样得到的?这些性质都是真命题吗?你能用逻辑推理的方法对它们进行证明吗?
二、精讲点拨
证明性质定理1:等腰三角形的两个底角相等
(简称:等边对等角)
已知:如图,在△ABC中,AB=AC,
求证:∠B=∠C
分析:常见辅助线做法(1)作底边上的高
(2)作顶角的平分线 (3)作底边上的中线
通过添加辅助线把三角形ABC分成两个
全等的三角形,只要证得被分成的两个
三角形全等即可得∠B=∠C
A
B
C
D
C
B
A
等腰三角形的性质定理1:等腰三角形的两个底角相等。
在△ABC中,
∵ AC=AB(已知)
∴ ∠B=∠C (等边对等角)
通过证明我们发现:等腰三角形的两个底角相等是真命题。可以作为证明其他命题的依据。
符号表示:
交流与发现
根据以上证明,我们还可以得到结论:等腰三角形底边上的高平分底边并且平分顶角。即得到∠BAD=∠CAD与BD=CD,于是得:
性质定理2: 等腰三角形的顶角平分线、底边上的中线、底上的高互相重合(简称“三线合一”)。
A
C
B
D
A
C
B
D
∥
∥
(2)∵AB=AC
图⑵
图⑶
∟
1
2
∥
A
C
B
D
1
2
性质定理2:符号语言的应用
∟
(1)∵AB=AC,
∴AD⊥BC,
BD=CD。
∠1=∠2,
∴AD⊥BC
BD=CD,
∠1=∠2。
(3)∵AB=AC,
AD⊥BC
∴BD=CD,
∠1=∠2。
图⑴
∟
∥
1
2
交流与发现
你能写出“性质定理1:等腰三角形的两个底角相等”的逆命题吗?如何证明这个逆命题是正确的?
如果一个三角形的两个角相等,那么这两个角所对的边也相等。(简称等角对等边)
已知:如图,在△ABC中,∠B=∠C。
求证: AB=AC
分析:是不是仍然可以做辅助线将原三角形
分成两个全等的三角形呢?试试看。
A
B
C
D
等腰三角形的判定定理:
如果一个三角形的两个角相等,那么这两个角所对的边也相等。(简称等角对等边)
C
B
A
符号表示:
在△ABC中,
∵∠B=∠C (已知)
∴ AC=AB(等角对等边)
利用等腰三角形的性质定理和判定定理证明:
学以致用
1.等边三角形的每个内角都是60°
2.三个角都相等的三角形是等边三 角形。
如果一个三角形的每个内角都等于60°,那么这个三角形是等边三角形。
2.当等腰三角形的顶角是60°时
这个逆命题是真命题
1.当等腰三角形的一个底角等于60°角时
思考:“等边三角形的每个内角都等于60°”的逆命题是什么?这个逆命题是真命题吗?
有一个角是60°的等腰三角形是等边三角形吗?
交流与发现
例2:已知:在△ABC中,AB=AC,D是AB上的一点,DE ⊥BC,交BC于点E,交CA的延长线于点F。
求证:AD=AF
分析:从已知出发先由已知AB=AC利用“等边对等角”推得∠B=∠C ,再由等角的余角相等推得∠BDE=∠F,进而得到∠ADF=∠F,最后根据“等角对等边”推出AD=AF。
练一练
1.已知,如图D是△ ABC内的一点,且DB=DC,BD平分∠ABC,CD平分∠ACB,
求证:AB=AC
C
B
A
D
2.在△ABC中,∠ABC、∠ACB的平分线相交
于点O,过点O作DE∥BC,分别交AB、AC于
点D、E。
请说明DE=BD+EC。
3.如图,△ABC是等边三角形,
BD是AC边上的高,延长BC至E,
使CE=CD。连接DE。
(1)∠E等于多少度?
(2)△DBE是什么三角形?
为什么?
三、系统总结
1.等腰三角形的判定方法有下列两种:
①定义②判定定理
2.等腰三角形的判定定理与性质定理的区别
条件和结论刚好相反
3.运用等腰三角形的判定定理时,应注意
在同一个三角形中
谢 谢
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
