数学:24.3相似三角形的性质课件(沪科版九年上)
文档属性
| 名称 | 数学:24.3相似三角形的性质课件(沪科版九年上) |  | |
| 格式 | rar | ||
| 文件大小 | 100.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-22 19:24:00 | ||
图片预览




文档简介
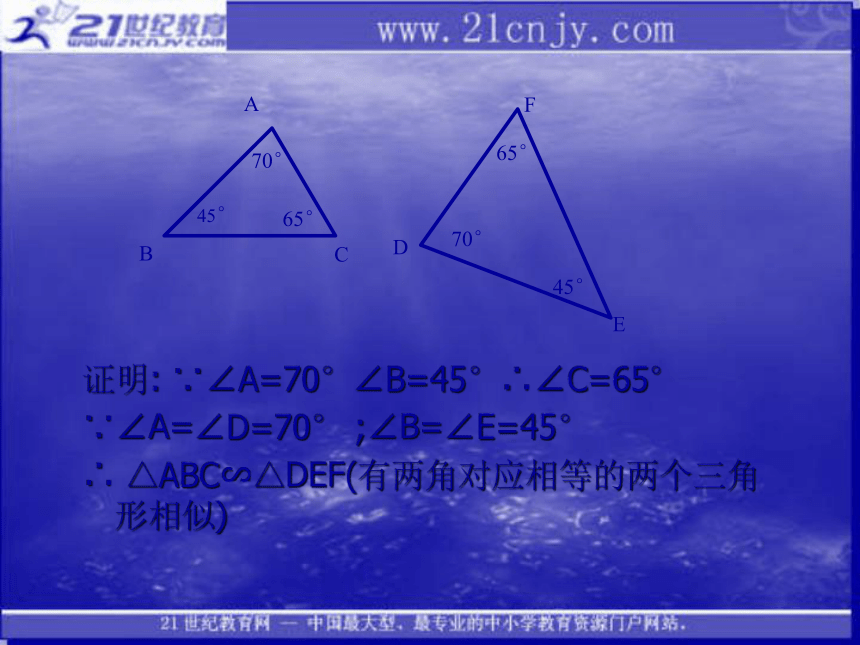
课件16张PPT。24.3相似三角形的性质试一试1.根据下列各图中给出的条件,确定△ABC与△DEF是否相似
证明: ∵∠A=70°∠B=45°∴∠C=65°
∵∠A=∠D=70° ;∠B=∠E=45°
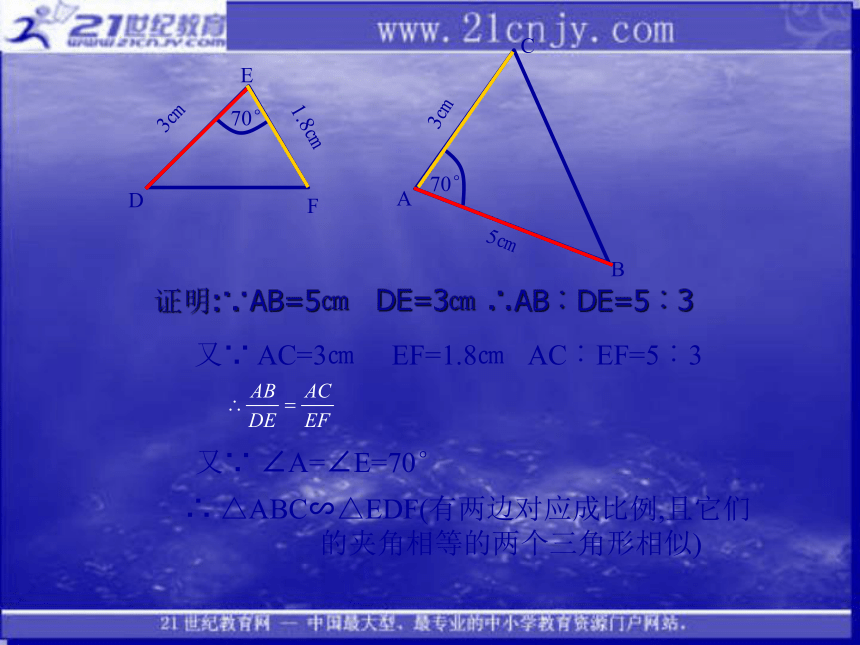
∴ △ABC∽△DEF(有两角对应相等的两个三角形相似)ABC45°70°65°DFE65°70°45°证明:∵AB=5㎝ DE=3㎝ ∴AB︰DE=5︰3
又∵ AC=3㎝ EF=1.8㎝ AC︰EF=5︰3又∵ ∠A=∠E=70°∴ △ABC∽△EDF(有两边对应成比例,且它们
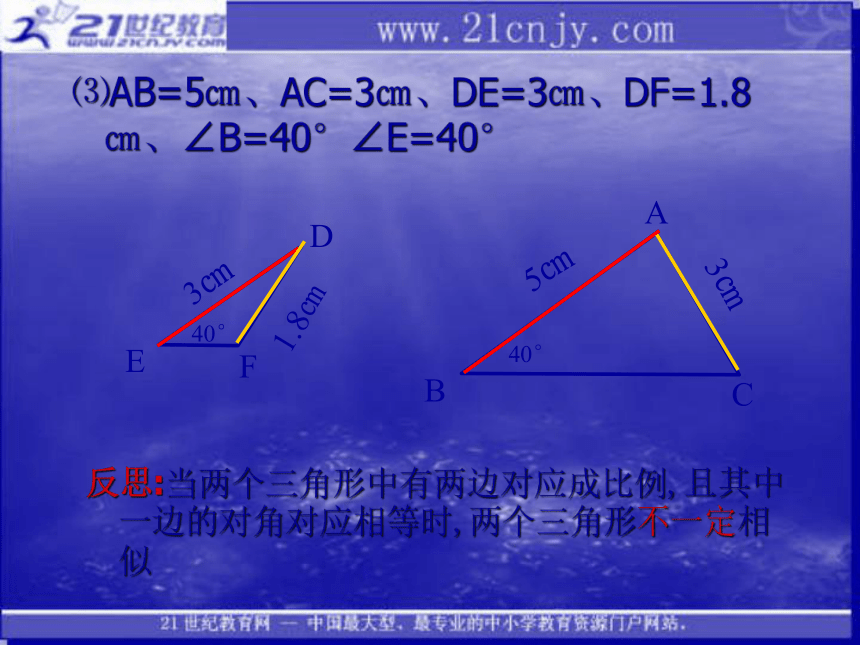
的夹角相等的两个三角形相似)⑶AB=5㎝、AC=3㎝、DE=3㎝、DF=1.8㎝、∠B=40°∠E=40°反思:当两个三角形中有两边对应成比例,且其中一边的对角对应相等时,两个三角形不一定相似∴ △ABC∽△DEF(有三边对应成比例的两个三角形 相似)
证明:2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEF边角EFD6㎝8㎝2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEF10 ㎝增加:DF=10,则可得△ABC和△DEF中有三边对应成比例,所以这两个三角形相似2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEFEFD6㎝增加:∠B=∠E,则可得△ABC和△DEF中有两边对应成比例且它们的夹角对应相等,所以这两个三角形相似8㎝2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEFEFD6㎝8㎝10 ㎝增加: DF=10, 则可得△ABC和△DEF中有三边对应成比例,所以这两个三角形相似增加: ∠B=∠E 则可得△ABC和△DEF中有两边对应成比例,且它们的夹角对应相等,所以这两个三角形相似回顾与反思: 当两个三角形中已有两边对应成比例而要证明两个三角形相似时 ,可以再设法寻找第三边与它们成比例;或找这两边的夹角对应相等 3.如图,已知:在△ABC中D、E分别是AC、AB上的点,且∠ADE=∠C,AD:AC= ︰2, AB=6, DE= ,求AE,BC的长.解:在△ABC和△ADE中
∵ ∠A=∠A ∠ADE=∠C
∴ △ABC∽△AED 已知如图: AD:AC=2︰3 AE= 3 AB= 4.5 求证: △ABC∽△AED.又∵ ∠EAD =∠BAC
∴△ABC∽△AED.解:探究新知 例题1 已知如图: △ABC∽△A′B′C′,相似比K=2︰3,又BD、B′D′分别是∠ABC、∠A′B′C′的平分线,求证BD︰B′D′=2︰3. 证明:∵△ABC∽△A′B′C′
∴∠A =∠A′; ∠ABC=∠A′B′C′思考:若K=a︰b,则可得AD︰A′D′的值为多少?由此可得什么结论相似三角形的性质:相似三角形对应角平分线的比等于相似比.∵△ABC与△A′B′C′的相似比 k=2︰3,.∴△ABD∽△A′B′D′ ∵BD、B′D′分别是∠ABC、∠A′B′C的平分线,
∴∠ABD=∠A′B′D′; 又∠A =∠A′;C′例题2 已知如图: △ABC∽△A′B′C′,相似比k,又AD、A′D′分别是BC、B′C′上的中线,求证AD︰A′D′=k. 证明:∵△ABC∽△A′B′C′结论:相似三角形对应中线的比等于相似比 ∵AD、A′D′分别是BC、B′C′ 的中线,∴∠B=∠B′又∵∠B=∠B′∴△ABD∽△A′B′D′猜测:相似三角形对应高的比等于________. 试一试∵AD⊥BC,A’D’⊥B’C’
∴∠ADB = ∠A’D’B’
又∵ ∠B = ∠B’
∴ △ABD∽△A’B’D’∴相似三角形对应高的比等于相似比. 相似比.已知如图: △ABC∽△A′B′C′,相似比k,又AD、A′D′分别是BC、B′C′上的高,求证:AD︰A′D′=k. 证明:∵△ABC∽△A′B′C′,相似比k
又AD、A′D′分别是BC、B′C′上的高 本课复习了相似三角形的基本特征及主要识别方法;并由此推出了相似三角形的另外三个重要的特征,即: 你通过这节课的学习有何收获? 相似三角形对应角平分线的比、对应中线的比、对应高的比都等于相似比。 事实上,若两个图形相似,其中所有的对应线段的比都等于相似比. 那么它的面积的比、周长比与相似比是什么关系呢?请同学们课后思考 .
∵∠A=∠D=70° ;∠B=∠E=45°
∴ △ABC∽△DEF(有两角对应相等的两个三角形相似)ABC45°70°65°DFE65°70°45°证明:∵AB=5㎝ DE=3㎝ ∴AB︰DE=5︰3
又∵ AC=3㎝ EF=1.8㎝ AC︰EF=5︰3又∵ ∠A=∠E=70°∴ △ABC∽△EDF(有两边对应成比例,且它们
的夹角相等的两个三角形相似)⑶AB=5㎝、AC=3㎝、DE=3㎝、DF=1.8㎝、∠B=40°∠E=40°反思:当两个三角形中有两边对应成比例,且其中一边的对角对应相等时,两个三角形不一定相似∴ △ABC∽△DEF(有三边对应成比例的两个三角形 相似)
证明:2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEF边角EFD6㎝8㎝2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEF10 ㎝增加:DF=10,则可得△ABC和△DEF中有三边对应成比例,所以这两个三角形相似2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEFEFD6㎝增加:∠B=∠E,则可得△ABC和△DEF中有两边对应成比例且它们的夹角对应相等,所以这两个三角形相似8㎝2.在△ABC和△DEF中若AB=9、BC=12㎝、AC=15㎝、DE=6㎝.EF=8㎝.请你再增加一个条件,使△ABC∽△DEFEFD6㎝8㎝10 ㎝增加: DF=10, 则可得△ABC和△DEF中有三边对应成比例,所以这两个三角形相似增加: ∠B=∠E 则可得△ABC和△DEF中有两边对应成比例,且它们的夹角对应相等,所以这两个三角形相似回顾与反思: 当两个三角形中已有两边对应成比例而要证明两个三角形相似时 ,可以再设法寻找第三边与它们成比例;或找这两边的夹角对应相等 3.如图,已知:在△ABC中D、E分别是AC、AB上的点,且∠ADE=∠C,AD:AC= ︰2, AB=6, DE= ,求AE,BC的长.解:在△ABC和△ADE中
∵ ∠A=∠A ∠ADE=∠C
∴ △ABC∽△AED 已知如图: AD:AC=2︰3 AE= 3 AB= 4.5 求证: △ABC∽△AED.又∵ ∠EAD =∠BAC
∴△ABC∽△AED.解:探究新知 例题1 已知如图: △ABC∽△A′B′C′,相似比K=2︰3,又BD、B′D′分别是∠ABC、∠A′B′C′的平分线,求证BD︰B′D′=2︰3. 证明:∵△ABC∽△A′B′C′
∴∠A =∠A′; ∠ABC=∠A′B′C′思考:若K=a︰b,则可得AD︰A′D′的值为多少?由此可得什么结论相似三角形的性质:相似三角形对应角平分线的比等于相似比.∵△ABC与△A′B′C′的相似比 k=2︰3,.∴△ABD∽△A′B′D′ ∵BD、B′D′分别是∠ABC、∠A′B′C的平分线,
∴∠ABD=∠A′B′D′; 又∠A =∠A′;C′例题2 已知如图: △ABC∽△A′B′C′,相似比k,又AD、A′D′分别是BC、B′C′上的中线,求证AD︰A′D′=k. 证明:∵△ABC∽△A′B′C′结论:相似三角形对应中线的比等于相似比 ∵AD、A′D′分别是BC、B′C′ 的中线,∴∠B=∠B′又∵∠B=∠B′∴△ABD∽△A′B′D′猜测:相似三角形对应高的比等于________. 试一试∵AD⊥BC,A’D’⊥B’C’
∴∠ADB = ∠A’D’B’
又∵ ∠B = ∠B’
∴ △ABD∽△A’B’D’∴相似三角形对应高的比等于相似比. 相似比.已知如图: △ABC∽△A′B′C′,相似比k,又AD、A′D′分别是BC、B′C′上的高,求证:AD︰A′D′=k. 证明:∵△ABC∽△A′B′C′,相似比k
又AD、A′D′分别是BC、B′C′上的高 本课复习了相似三角形的基本特征及主要识别方法;并由此推出了相似三角形的另外三个重要的特征,即: 你通过这节课的学习有何收获? 相似三角形对应角平分线的比、对应中线的比、对应高的比都等于相似比。 事实上,若两个图形相似,其中所有的对应线段的比都等于相似比. 那么它的面积的比、周长比与相似比是什么关系呢?请同学们课后思考 .
