4.1 对数的概念 课件 (共26张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 4.1 对数的概念 课件 (共26张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第四章
4.1 对数的概念
1.了解对数的概念.
2.弄清指数与对数之间的关系,并对它们进行灵活的转化,对于常用对数、自然对数的简记方法要熟悉.
3.了解对数、常用对数、自然对数的概念,并体会将指数式化为对数式,将对数式化为指数式的含义与作用.
1光年为9 460 730 472 580 800米.
一个人走完一光年需要 大约196,362,193年,约2亿年.
英国数学家卡斯纳(E.Kasner)的侄子创造了单词“googol”
——大数,10100
指数的指数——超指数
象征无与伦比的搜索能力
很多巨大的数可以用指数来表示
感受指数
在16至17世纪,天文学开始迅速发展,天文学家为了计算一个行星的位置,
时常需要耗费几个月甚至几年的时间,问题主要就集中在“大数”运算上.
因此,改进运算方法成为了天文学家们的当务之急.
一、对数的产生
数学家们也在试图改进运算方法,他们发现借助指数幂是有效的方法.
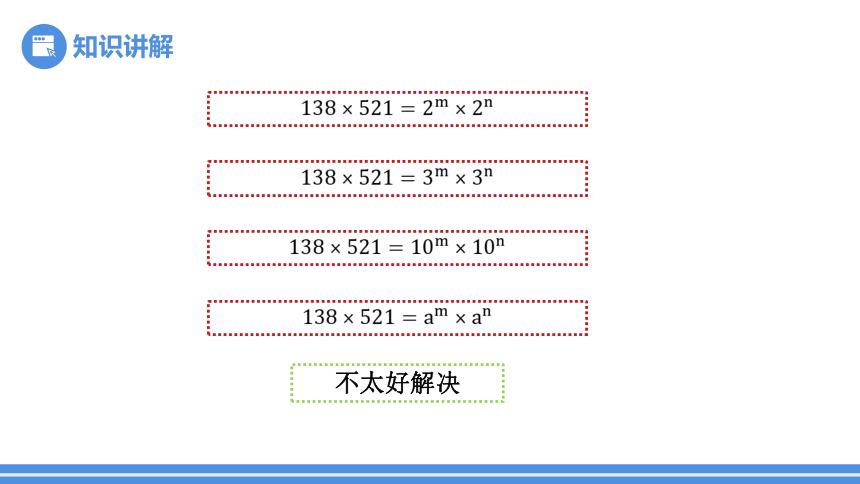
在不使用计算器的前提下,计算256×4096=1048576.
不太好解决
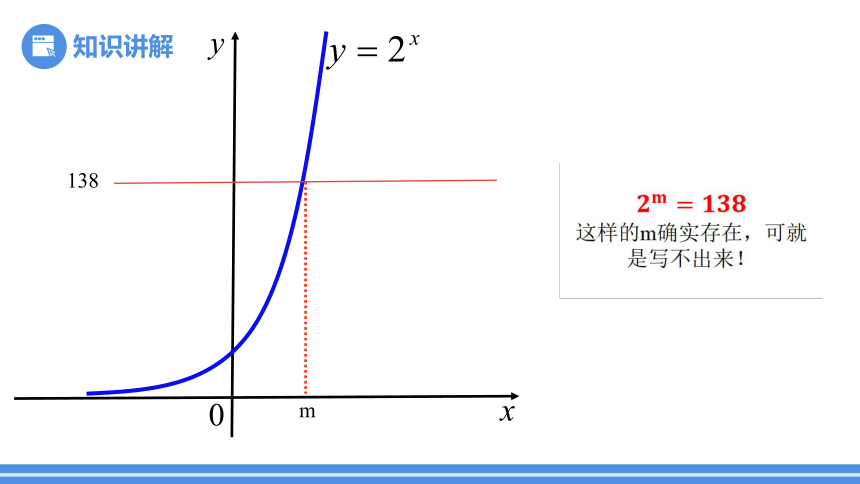
m
138
这样的m确实存在,可就是写不出来!
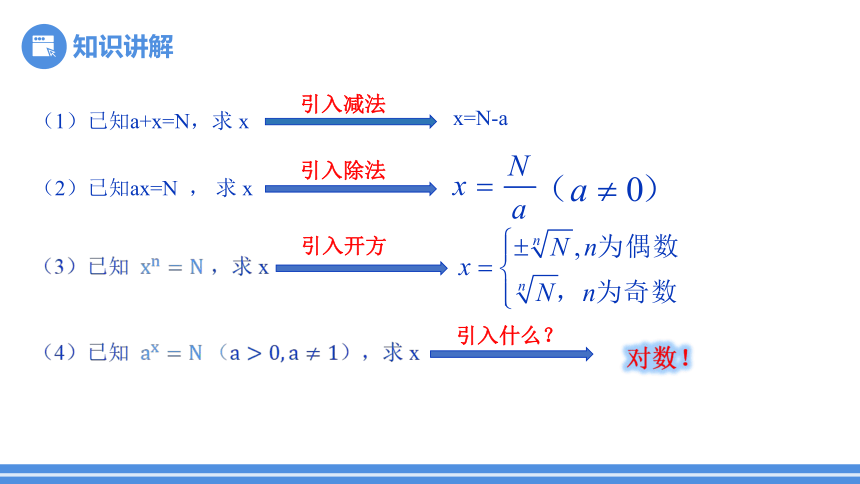
引入减法
x=N-a
引入除法
引入开方
引入什么?
对数!
(1)已知a+x=N,求 x
(2)已知ax=N , 求 x
(3)已知 ,求 x
(4)已知 ),求 x
二、对数的定义
一般地,如果 ,那么数x叫做以a为底N的对数(logarithm),记作 .
其中a叫做对数的底数,N叫做真数,读作:以a为底N的对数.
表示一种运算
1.有什么关系,代表什么含义?
2.为什么规定
3.为什么零
阅读教材 思考交流
底数
底数
指数
对数
幂
真数
?
关系图
2.在对数的定义中为什么规定a>0,且a≠1
因为对数概念源出于指数,对数式logaN=b是由指数式ab=N转化而来,对数的底数就是指数的底数,而ab=N中要使它对任意实数b都有意义,必须a>0,且a≠1,所以对数式中也必须要求a>0,且a≠1.
请判断“因为(-2)4=16,所以log(-2)16=4”这个说法正确吗
不正确.因为要求底数大于0,否则指数式与对数式不能互化.
为什么零和负数没有对数?
由对数的定义:ax=N(a>0且a≠1),则总有N>0,所以转化为对数式x=logaN时,不存在N≤0的情况.
例1. 已知对数log(1-a)(a+2)有意义,求实数a的取值范围.
[解] 由于对数log(1-a)(a+2)有意义,则有,解得-2所以实数a的取值范围是(-2,0)∪(0,1).
三、两种特殊的对数
(1)常用对数:当对数的底数a=10时,通常称之为常用对数,并将log10N简记为lg N .
(2)自然对数:在科学技术领域,常常使用以无理数e=2.718 28
…为底数的对数,称之为自然对数,并将logeN简记为ln N .
对数基本性质
(1)负数和零没有对数;
(2)若a>0,且a≠1,则loga1= ,logaa= ;
(3)= .
答案:(2)0 1 (3)N
例2. 将下列指数式化为对数式,对数式化为指数式:
(1)2-7= ; (2)33=27;
(3)lo32= -5; (4)lg 0.001=-3.
解:(1)因为2-7=,所以log2=-7.
(2)因为33=27,所以log327=3.
(3)因为lo32=-5,所以=32.
(4)因为lg 0.001=-3,所以10-3=0.001.
1.对数式与指数式关系图
对数式logaN=b是由指数式ab=N变换而来的,两式底数相同,对数式中的真数N就是指数式中的幂的值N,而对数值b是指数式中的幂指数.
2.并非所有指数式都可以直接化为对数式.如(-3)2=9就不能直接写成log(-3)9=2,只有当a>0,且a≠1,N>0时,才有ax=N x=logaN.
互化经验
,
解析:(1)由log3(log2(lg x))=0,可得log2(lg x)=1,
所以lg x=2,所以x=100.
(2)已知log2[log3(log4x)]=log3[log4(log2y)]=0,求x+y的值.
解:因为log2[log3(log4x)]=0,
所以log3(log4x)=1,所以log4x=3,所以x=43=64.
同理可得y=24=16所以x+y=80.
求值经验
利用对数性质求解的两类问题的解法
(1)求多重对数式的值解题方法是由内到外,如求loga(logbc)的值,先求logbc的值,
再求loga(logbc)的值.
(2)已知多重对数式的值,求变量值,应从外到内求,逐步脱去
(3)求解形如“(a>0,且a≠1)”的值的一般步骤
①借助指数幂的运算,使其变形为·a±m.
②借助恒等式=N及指数幂的运算求值.
1.判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)1的对数是1.( × )
(2)2log22-1=-1.( × )
(3)对数运算的实质是求幂指数.( √ )
?
?
?
2.下列指数式与对数式互化不正确的一组是( )
A.e0=1与ln 1=0
B. 与
C.log39=2与
D.log77=1与71=7
答案:C
解析:根据ab=N b=logaN可知,A,B,D均正确,C不正确.
log39=2 32=9,
3.若有意义,求x的取值范围.
解:由题意,有
解得x>10,且x≠11.
故x的取值范围是{x|x>10,且x≠11}.
4.求下列各式中x的值
(1)log2(log5x)=0;
(2)log3(lg x)=1;
(3)log3(log4(log5x))=0.
解:(1)∵log2(log5x)=0,∴log5x=20=1,∴x=51=5.
(2)∵log3(lg x)=1,∴lg x=31=3,∴x=103=1 000.
(3)由log3(log4(log5x))=0可得log4(log5x)=1,故log5x=4,所以x=54=625.
1.对数函数概念;
2.对数的基本性质.
数学素养:通过指数式与对数式的互化及对数的基本性质的学习,培养逻辑推理素养与数学运算素养.
第四章
4.1 对数的概念
1.了解对数的概念.
2.弄清指数与对数之间的关系,并对它们进行灵活的转化,对于常用对数、自然对数的简记方法要熟悉.
3.了解对数、常用对数、自然对数的概念,并体会将指数式化为对数式,将对数式化为指数式的含义与作用.
1光年为9 460 730 472 580 800米.
一个人走完一光年需要 大约196,362,193年,约2亿年.
英国数学家卡斯纳(E.Kasner)的侄子创造了单词“googol”
——大数,10100
指数的指数——超指数
象征无与伦比的搜索能力
很多巨大的数可以用指数来表示
感受指数
在16至17世纪,天文学开始迅速发展,天文学家为了计算一个行星的位置,
时常需要耗费几个月甚至几年的时间,问题主要就集中在“大数”运算上.
因此,改进运算方法成为了天文学家们的当务之急.
一、对数的产生
数学家们也在试图改进运算方法,他们发现借助指数幂是有效的方法.
在不使用计算器的前提下,计算256×4096=1048576.
不太好解决
m
138
这样的m确实存在,可就是写不出来!
引入减法
x=N-a
引入除法
引入开方
引入什么?
对数!
(1)已知a+x=N,求 x
(2)已知ax=N , 求 x
(3)已知 ,求 x
(4)已知 ),求 x
二、对数的定义
一般地,如果 ,那么数x叫做以a为底N的对数(logarithm),记作 .
其中a叫做对数的底数,N叫做真数,读作:以a为底N的对数.
表示一种运算
1.有什么关系,代表什么含义?
2.为什么规定
3.为什么零
阅读教材 思考交流
底数
底数
指数
对数
幂
真数
?
关系图
2.在对数的定义中为什么规定a>0,且a≠1
因为对数概念源出于指数,对数式logaN=b是由指数式ab=N转化而来,对数的底数就是指数的底数,而ab=N中要使它对任意实数b都有意义,必须a>0,且a≠1,所以对数式中也必须要求a>0,且a≠1.
请判断“因为(-2)4=16,所以log(-2)16=4”这个说法正确吗
不正确.因为要求底数大于0,否则指数式与对数式不能互化.
为什么零和负数没有对数?
由对数的定义:ax=N(a>0且a≠1),则总有N>0,所以转化为对数式x=logaN时,不存在N≤0的情况.
例1. 已知对数log(1-a)(a+2)有意义,求实数a的取值范围.
[解] 由于对数log(1-a)(a+2)有意义,则有,解得-2
三、两种特殊的对数
(1)常用对数:当对数的底数a=10时,通常称之为常用对数,并将log10N简记为lg N .
(2)自然对数:在科学技术领域,常常使用以无理数e=2.718 28
…为底数的对数,称之为自然对数,并将logeN简记为ln N .
对数基本性质
(1)负数和零没有对数;
(2)若a>0,且a≠1,则loga1= ,logaa= ;
(3)= .
答案:(2)0 1 (3)N
例2. 将下列指数式化为对数式,对数式化为指数式:
(1)2-7= ; (2)33=27;
(3)lo32= -5; (4)lg 0.001=-3.
解:(1)因为2-7=,所以log2=-7.
(2)因为33=27,所以log327=3.
(3)因为lo32=-5,所以=32.
(4)因为lg 0.001=-3,所以10-3=0.001.
1.对数式与指数式关系图
对数式logaN=b是由指数式ab=N变换而来的,两式底数相同,对数式中的真数N就是指数式中的幂的值N,而对数值b是指数式中的幂指数.
2.并非所有指数式都可以直接化为对数式.如(-3)2=9就不能直接写成log(-3)9=2,只有当a>0,且a≠1,N>0时,才有ax=N x=logaN.
互化经验
,
解析:(1)由log3(log2(lg x))=0,可得log2(lg x)=1,
所以lg x=2,所以x=100.
(2)已知log2[log3(log4x)]=log3[log4(log2y)]=0,求x+y的值.
解:因为log2[log3(log4x)]=0,
所以log3(log4x)=1,所以log4x=3,所以x=43=64.
同理可得y=24=16所以x+y=80.
求值经验
利用对数性质求解的两类问题的解法
(1)求多重对数式的值解题方法是由内到外,如求loga(logbc)的值,先求logbc的值,
再求loga(logbc)的值.
(2)已知多重对数式的值,求变量值,应从外到内求,逐步脱去
(3)求解形如“(a>0,且a≠1)”的值的一般步骤
①借助指数幂的运算,使其变形为·a±m.
②借助恒等式=N及指数幂的运算求值.
1.判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)1的对数是1.( × )
(2)2log22-1=-1.( × )
(3)对数运算的实质是求幂指数.( √ )
?
?
?
2.下列指数式与对数式互化不正确的一组是( )
A.e0=1与ln 1=0
B. 与
C.log39=2与
D.log77=1与71=7
答案:C
解析:根据ab=N b=logaN可知,A,B,D均正确,C不正确.
log39=2 32=9,
3.若有意义,求x的取值范围.
解:由题意,有
解得x>10,且x≠11.
故x的取值范围是{x|x>10,且x≠11}.
4.求下列各式中x的值
(1)log2(log5x)=0;
(2)log3(lg x)=1;
(3)log3(log4(log5x))=0.
解:(1)∵log2(log5x)=0,∴log5x=20=1,∴x=51=5.
(2)∵log3(lg x)=1,∴lg x=31=3,∴x=103=1 000.
(3)由log3(log4(log5x))=0可得log4(log5x)=1,故log5x=4,所以x=54=625.
1.对数函数概念;
2.对数的基本性质.
数学素养:通过指数式与对数式的互化及对数的基本性质的学习,培养逻辑推理素养与数学运算素养.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
