5.2.2 用函数模型解决实际问题 课件(共20张PPT) 2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 5.2.2 用函数模型解决实际问题 课件(共20张PPT) 2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 22:18:45 | ||
图片预览






文档简介
(共20张PPT)
5.2.2 用函数模型解决实际问题
1.能利用已知函数模型解决实际问题.
情境:数学模型是针对某种事物的主要特征、主要关系,用形式化的数学语言,抽象概括地、简化近似地表述出来的一种数学结构.其中,函数模型是应用最广泛的数学模型之一.实际问题一旦被认定是函数关系,就可以通过研究这个函数的性质,使问题得到解决.
问题1 在之前的学习中,我们学过哪些函数?
名称 解析式 条件
一次函数模型
反比例函数模型
二次函数模型
指数函数模型 ,
对数函数模型 ,
幂函数模型
例1 某国年至年国内生产总值(单位:万亿元)如下表所示:
年份 2018 2019 2020 2021
x(年) 0 1 2 3
生产总值(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
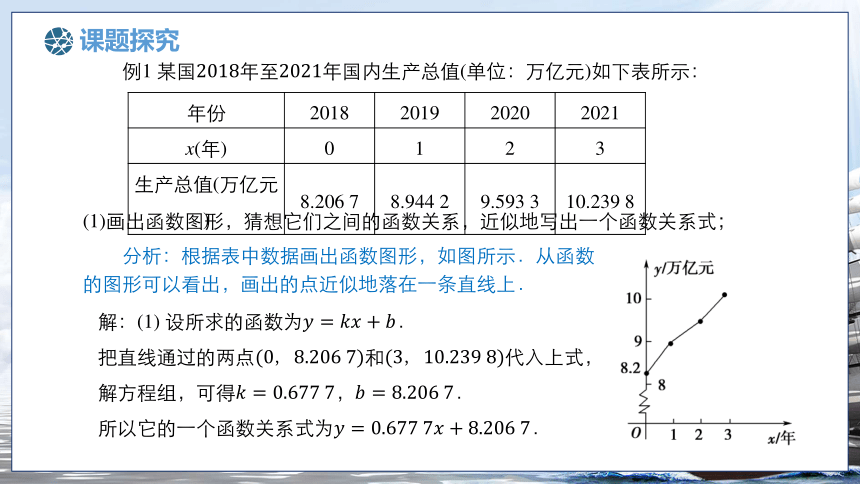
(1)画出函数图形,猜想它们之间的函数关系,近似地写出一个函数关系式;
解:(1) 设所求的函数为.
把直线通过的两点和代入上式,
解方程组,可得,.
所以它的一个函数关系式为.
分析:根据表中数据画出函数图形,如图所示.从函数的图形可以看出,画出的点近似地落在一条直线上.
例1 某国年至年国内生产总值(单位:万亿元)如下表所示:
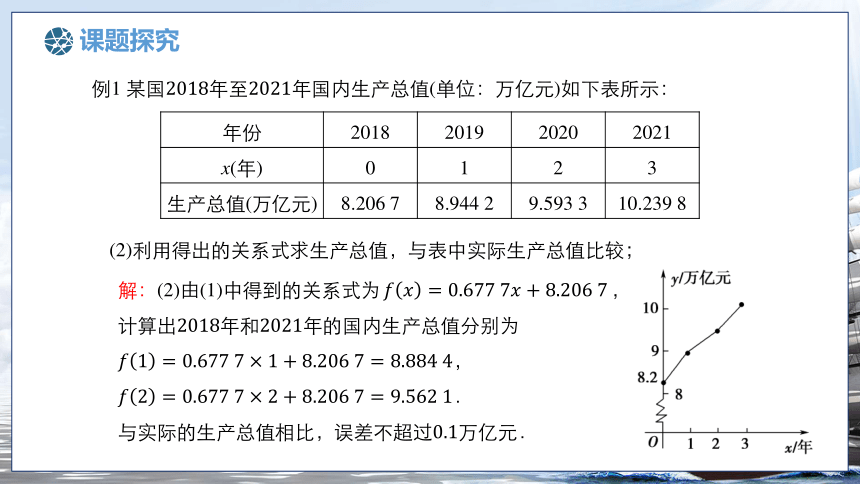
(2)利用得出的关系式求生产总值,与表中实际生产总值比较;
解:(2)由(1)中得到的关系式为,
计算出年和年的国内生产总值分别为
,
.
与实际的生产总值相比,误差不超过万亿元.
年份 2018 2019 2020 2021
x(年) 0 1 2 3
生产总值(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
例1 某国年至年国内生产总值(单位:万亿元)如下表所示:
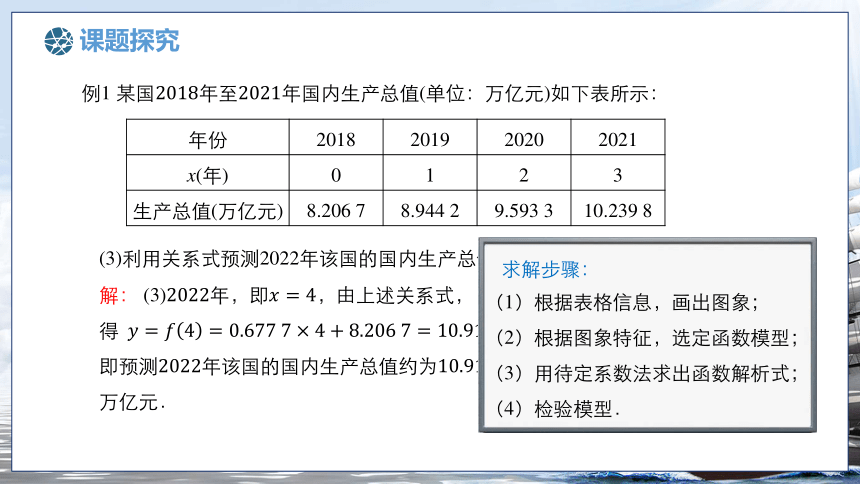
(3)利用关系式预测2022年该国的国内生产总值.
解: (3)年,即,由上述关系式,
得,
即预测年该国的国内生产总值约为万亿元.
年份 2018 2019 2020 2021
x(年) 0 1 2 3
生产总值(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
(1)根据表格信息,画出图象;
(2)根据图象特征,选定函数模型;
(3)用待定系数法求出函数解析式;
(4)检验模型.
求解步骤:
例2 如图1是某公共汽车线路收支差额元与乘客量的图象.
(1)试说明图上点、点以及射线上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象,说明这两种建议的意义吗?
(3)此问题中直线斜率的实际意义是什么?
(4)图、图、图中的票价分别是多少元?
解:(1)点表示无人乘车时收支差额为元,
点表示有人乘车时收支差额为元,
线段上的点表示亏损,
延长线上的点表示盈利.
图1
图2
图3
例2 如图1是某公共汽车线路收支差额元与乘客量的图象.
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象,说明这两种建议的意义吗?
(3)此问题中直线斜率的实际意义是什么?
(4)图、图、图中的票价分别是多少元?
解: (2)图的建议是降低成本,票价不变,
图的建议是提高票价.
(3)斜率表示票价.
(4)图、中的票价是元,
图中的票价是元.
与轴交点由变为
斜率不变
与轴交点不变
斜率变大
图1
图2
图3
斜率
特征
特征
例3 要建造一段的高速公路,工程队需要把人分成两组,一组完成一段的软土地带公路的建造任务,同时另一组完成剩下的的硬土地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是人·天和人·天.问:如何安排两组的人数,才能使全队筑路工期最短?
分析:设在软土地带工作的人数为人,
则在硬土地带工作的人数为人,
在软土地带筑路时间为:,
在硬土土地带筑路时间为:,
取较大值得到关于
全队筑路时间的函数
最小值
例3 要建造一段的高速公路,工程队需要把人分成两组,一组完成一段的软土地带公路的建造任务,同时另一组完成剩下的的硬土地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是人·天和人·天.问:如何安排两组的人数,才能使全队筑路工期最短?
解:设在软土地带工作的人数为人,则在硬土地带工作的人数为人.
根据题意,在软土地带筑路时间为,
在硬土地带筑路时间为,其中,.
因为函数在区间上是减函数,函数在区间上是增函数,
所以全队筑路工期为:
例3 要建造一段的高速公路,工程队需要把人分成两组,一组完成一段的软土地带公路的建造任务,同时另一组完成剩下的的硬土地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是人·天和人·天.问:如何安排两组的人数,才能使全队筑路工期最短?
由,即,得.从而.
因为函数在区间上递减,在区间上递增,所以是函数的最小值点.但不是整数,于是计算和,其中较小者即为所求.
经计算,,.
于是,当安排人到软土地带工作,人到硬土地带工作时,可以使全队筑路工期最短.
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
分析:首先要做一些假设:
每天需同样多的元件;
其他费用可以作为常数看待.
总费用
库存费
手续费
其他费用
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
解:将个元件所需的总费用记为元,一年总库存费记为元,购买元件总手续费记为元,其他费用记为元(为常数),则.
若每年平均进货次(),则每次的进货量为个.
假设用完个元件的时间为年,在内,时刻的库存量为,
满足,,.
解得 .
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
如图,阴影部分的面积是第一个时间段内需支付库存费的库存量的总和,相当于在年内每一时刻需支付库存费的库存量均为个.
在年内,每个元件的库存费为元,
则个元件的库存费为(元).
一年总库存费为:(元).
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
另外,元,所以.
由基本不等式,得.
当且仅当,即时,上面的不等式取等号,此时总费用最少,故每年进货次最经济.
存贮模型
1.判断:
(1)在建立实际问题的函数模型时,除了要考虑变量的数学意义,还要考虑变量的实际意义.( )
(2)由函数模型得到的解就是实际问题的解.( )
解: (1)正确;
(2)由函数模型得到的解,要回到实际问题中去,验证是否符合实际问题,然后才能确定实际问题的解;故错误.
×
√
2.某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往,他先前进了,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了,当他想起诗句“不到长城非好汉”时,便调转车头继续前进,则该同学离起点的距离与时间的函数关系图象大致为( )
C
A
B
C
D
解:由题意知,在前的路程中,是关于时间的一次函数,图象特征是直线上升.由于中间休息了一段时间,该段时间的图象应是平行于横轴的一条线段.然后原路返回,图象下降,再调转车头继续前进,则直线一致上升.故选C.
解:由题意得窗框总长,
∴,∴.
由得,
当时,,
此时,
所以,当矩形的高等于半圆的半径时,窗户透光面积最大.
3. 要在墙上开一个上部为半圆,下部为矩形的窗户,如图所示,窗框为定长的条件下,要使窗户透光面积最大,窗户应具有怎样的尺寸?
建立函数模型解决实际问题的基本思路:
实际问题
数学问题
实际问题的结论
数学问题的解
转化
确定函数模型
符合实际
问题解决
5.2.2 用函数模型解决实际问题
1.能利用已知函数模型解决实际问题.
情境:数学模型是针对某种事物的主要特征、主要关系,用形式化的数学语言,抽象概括地、简化近似地表述出来的一种数学结构.其中,函数模型是应用最广泛的数学模型之一.实际问题一旦被认定是函数关系,就可以通过研究这个函数的性质,使问题得到解决.
问题1 在之前的学习中,我们学过哪些函数?
名称 解析式 条件
一次函数模型
反比例函数模型
二次函数模型
指数函数模型 ,
对数函数模型 ,
幂函数模型
例1 某国年至年国内生产总值(单位:万亿元)如下表所示:
年份 2018 2019 2020 2021
x(年) 0 1 2 3
生产总值(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
(1)画出函数图形,猜想它们之间的函数关系,近似地写出一个函数关系式;
解:(1) 设所求的函数为.
把直线通过的两点和代入上式,
解方程组,可得,.
所以它的一个函数关系式为.
分析:根据表中数据画出函数图形,如图所示.从函数的图形可以看出,画出的点近似地落在一条直线上.
例1 某国年至年国内生产总值(单位:万亿元)如下表所示:
(2)利用得出的关系式求生产总值,与表中实际生产总值比较;
解:(2)由(1)中得到的关系式为,
计算出年和年的国内生产总值分别为
,
.
与实际的生产总值相比,误差不超过万亿元.
年份 2018 2019 2020 2021
x(年) 0 1 2 3
生产总值(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
例1 某国年至年国内生产总值(单位:万亿元)如下表所示:
(3)利用关系式预测2022年该国的国内生产总值.
解: (3)年,即,由上述关系式,
得,
即预测年该国的国内生产总值约为万亿元.
年份 2018 2019 2020 2021
x(年) 0 1 2 3
生产总值(万亿元) 8.206 7 8.944 2 9.593 3 10.239 8
(1)根据表格信息,画出图象;
(2)根据图象特征,选定函数模型;
(3)用待定系数法求出函数解析式;
(4)检验模型.
求解步骤:
例2 如图1是某公共汽车线路收支差额元与乘客量的图象.
(1)试说明图上点、点以及射线上的点的实际意义;
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象,说明这两种建议的意义吗?
(3)此问题中直线斜率的实际意义是什么?
(4)图、图、图中的票价分别是多少元?
解:(1)点表示无人乘车时收支差额为元,
点表示有人乘车时收支差额为元,
线段上的点表示亏损,
延长线上的点表示盈利.
图1
图2
图3
例2 如图1是某公共汽车线路收支差额元与乘客量的图象.
(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象,说明这两种建议的意义吗?
(3)此问题中直线斜率的实际意义是什么?
(4)图、图、图中的票价分别是多少元?
解: (2)图的建议是降低成本,票价不变,
图的建议是提高票价.
(3)斜率表示票价.
(4)图、中的票价是元,
图中的票价是元.
与轴交点由变为
斜率不变
与轴交点不变
斜率变大
图1
图2
图3
斜率
特征
特征
例3 要建造一段的高速公路,工程队需要把人分成两组,一组完成一段的软土地带公路的建造任务,同时另一组完成剩下的的硬土地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是人·天和人·天.问:如何安排两组的人数,才能使全队筑路工期最短?
分析:设在软土地带工作的人数为人,
则在硬土地带工作的人数为人,
在软土地带筑路时间为:,
在硬土土地带筑路时间为:,
取较大值得到关于
全队筑路时间的函数
最小值
例3 要建造一段的高速公路,工程队需要把人分成两组,一组完成一段的软土地带公路的建造任务,同时另一组完成剩下的的硬土地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是人·天和人·天.问:如何安排两组的人数,才能使全队筑路工期最短?
解:设在软土地带工作的人数为人,则在硬土地带工作的人数为人.
根据题意,在软土地带筑路时间为,
在硬土地带筑路时间为,其中,.
因为函数在区间上是减函数,函数在区间上是增函数,
所以全队筑路工期为:
例3 要建造一段的高速公路,工程队需要把人分成两组,一组完成一段的软土地带公路的建造任务,同时另一组完成剩下的的硬土地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是人·天和人·天.问:如何安排两组的人数,才能使全队筑路工期最短?
由,即,得.从而.
因为函数在区间上递减,在区间上递增,所以是函数的最小值点.但不是整数,于是计算和,其中较小者即为所求.
经计算,,.
于是,当安排人到软土地带工作,人到硬土地带工作时,可以使全队筑路工期最短.
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
分析:首先要做一些假设:
每天需同样多的元件;
其他费用可以作为常数看待.
总费用
库存费
手续费
其他费用
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
解:将个元件所需的总费用记为元,一年总库存费记为元,购买元件总手续费记为元,其他费用记为元(为常数),则.
若每年平均进货次(),则每次的进货量为个.
假设用完个元件的时间为年,在内,时刻的库存量为,
满足,,.
解得 .
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
如图,阴影部分的面积是第一个时间段内需支付库存费的库存量的总和,相当于在年内每一时刻需支付库存费的库存量均为个.
在年内,每个元件的库存费为元,
则个元件的库存费为(元).
一年总库存费为:(元).
例4 某公司每年需要某种计算机元件个,每次购买元件需手续费元,每个元件的库存费是每年元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)?
另外,元,所以.
由基本不等式,得.
当且仅当,即时,上面的不等式取等号,此时总费用最少,故每年进货次最经济.
存贮模型
1.判断:
(1)在建立实际问题的函数模型时,除了要考虑变量的数学意义,还要考虑变量的实际意义.( )
(2)由函数模型得到的解就是实际问题的解.( )
解: (1)正确;
(2)由函数模型得到的解,要回到实际问题中去,验证是否符合实际问题,然后才能确定实际问题的解;故错误.
×
√
2.某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往,他先前进了,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了,当他想起诗句“不到长城非好汉”时,便调转车头继续前进,则该同学离起点的距离与时间的函数关系图象大致为( )
C
A
B
C
D
解:由题意知,在前的路程中,是关于时间的一次函数,图象特征是直线上升.由于中间休息了一段时间,该段时间的图象应是平行于横轴的一条线段.然后原路返回,图象下降,再调转车头继续前进,则直线一致上升.故选C.
解:由题意得窗框总长,
∴,∴.
由得,
当时,,
此时,
所以,当矩形的高等于半圆的半径时,窗户透光面积最大.
3. 要在墙上开一个上部为半圆,下部为矩形的窗户,如图所示,窗框为定长的条件下,要使窗户透光面积最大,窗户应具有怎样的尺寸?
建立函数模型解决实际问题的基本思路:
实际问题
数学问题
实际问题的结论
数学问题的解
转化
确定函数模型
符合实际
问题解决
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
