2024-2025学年浙教版七年级上册期中拔高练习(含解析)
文档属性
| 名称 | 2024-2025学年浙教版七年级上册期中拔高练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-25 09:45:42 | ||
图片预览



文档简介
浙教版七年级上册期中拔高练习
一、数字类规律探索
1.如图,图1所示的数字规律表,已知图2是从图1中按未显示部分截取下来的一部分,则△处的数字不可能是( )
A.75 B.50 C.26 D.9
2.记的所有正因数为,,…,,则( )
A. B. C. D.
3.在数学上,常用符号来简洁地表示多个数求和,例如表示把代数式取为1,2,3,……,99,100时的代数式的值分别求和,即结果为,则的结果为( )
A. B. C. D.
4.将正整数按下表规律排列:表中数2在第二行、第一列,与有序数对对应,数5与对应;数14与对应;根据这一规律,数2023对应的有序数对为( )
第一列 二列 三列 四列 五列 …
第一行 1 4 5 16 17
第二行 2 3 6 15 …
第三行 9 8 7 14
第四行 10 11 12 13
第五行
…
A. B. C. D.
5.我们规定:表示不超过x的最大整数.如:,.现已知对所有正整数n成立,则的值为 .
6.现有一列数:,,,,,,(为正整数),规定,,,,,则的值为 .
7.已知有理数a≠1,我们把称为a的差倒数,如:2的差倒数是=﹣1,﹣1的差倒数是.如果a1=﹣2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……依此类推,那么a1+a2+…+a100的值是 .
8.若a是不为2的有理数,我们把称为a的“牛顿数”.如3的“牛顿数”是,的“牛顿数”是,已知,是的“牛顿数”,是的“牛顿数”,是的“牛顿数”,…,依此类推,则 .
9.在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地毯”,如图1,计算,将乘数82记入上行,乘数34记入右行,然后用乘数82的每位数字乘以乘数34的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2788.如图2,用“铺地毯”的方法表示两个两位数相乘,则= ,= .
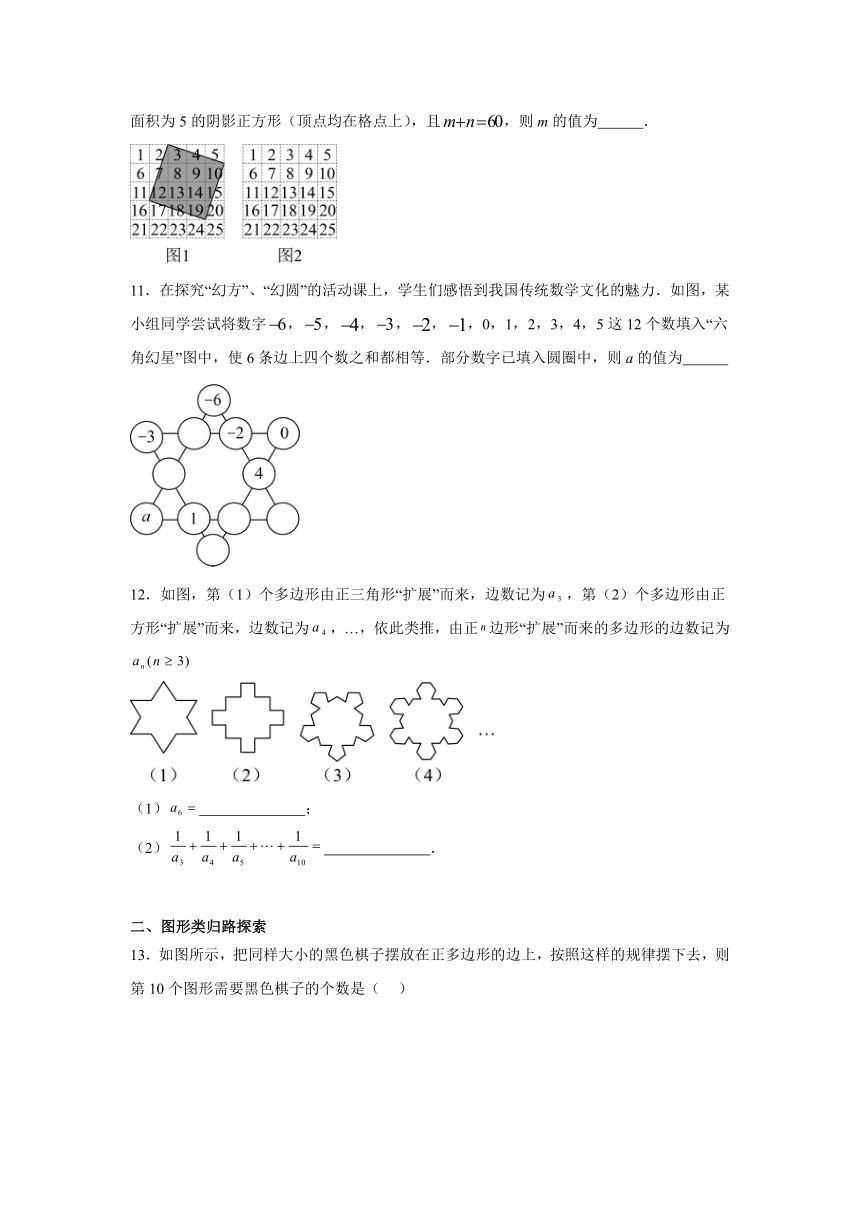
10.如图,在的方格中,每个小方格的边长为1且标记数字,在方格中画阴影正方形.现规定被阴影正方形全部覆盖的小方格,其数值之和记为m,部分覆盖的小方格,其数值之和的一半记为n.以图1中阴影正方形为例,.若在图2中画一个面积为5的阴影正方形(顶点均在格点上),且,则m的值为 .
11.在探究“幻方”、“幻圆”的活动课上,学生们感悟到我国传统数学文化的魅力.如图,某小组同学尝试将数字,,,,,,0,1,2,3,4,5这12个数填入“六角幻星”图中,使6条边上四个数之和都相等.部分数字已填入圆圈中,则a的值为
12.如图,第(1)个多边形由正三角形“扩展”而来,边数记为,第(2)个多边形由正方形“扩展”而来,边数记为,…,依此类推,由正边形“扩展”而来的多边形的边数记为
(1) ;
(2) .
二、图形类归路探索
13.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10个图形需要黑色棋子的个数是( )
A.120个 B.122个 C.130个 D.132个
14.电子跳蚤游戏盘(如图)为,,,,如果电子跳蚤开始时在BC边的点,,第一步跳蚤从跳到AC边上点,且;第二步跳蚤从跳到AB边上点,且;第三步跳蚤从跳回到BC边上点,且;……跳蚤按上述规则跳下去,第n次落点为.则与之间的距离为( )
A.0 B.1 C.4 D.5
15.用边长相等的正方形和等边三角形卡片按如图所示的方式和规律拼出图形.拼第1个图形所用两种卡片的总数为7枚,拼第2个图形所用两种卡片的总数为12枚若按照这样的规律拼出的第个图形中,所用正方形卡片比等边三角形卡片多10枚,则拼第个图形所用两种卡片的总数为( )
A.57枚 B.52枚 C.50枚 D.47枚
16.用若干根长为1的火柴恰好可以拼成如图1所示的47个边长为1的正方形,若将这些火柴按如图2所示的方式拼,则可以拼出 个边长为1的正方形.
17.用正方形按如图所示的规律拼图案,其中第①个图案中有个正方形,第②个图案中有个正方形,第③个图案中有个正方形,第④个图案中有个正方形,此规律排列下去,则第⑨个图案中正方形的个数为 .
三、整式加减的应用
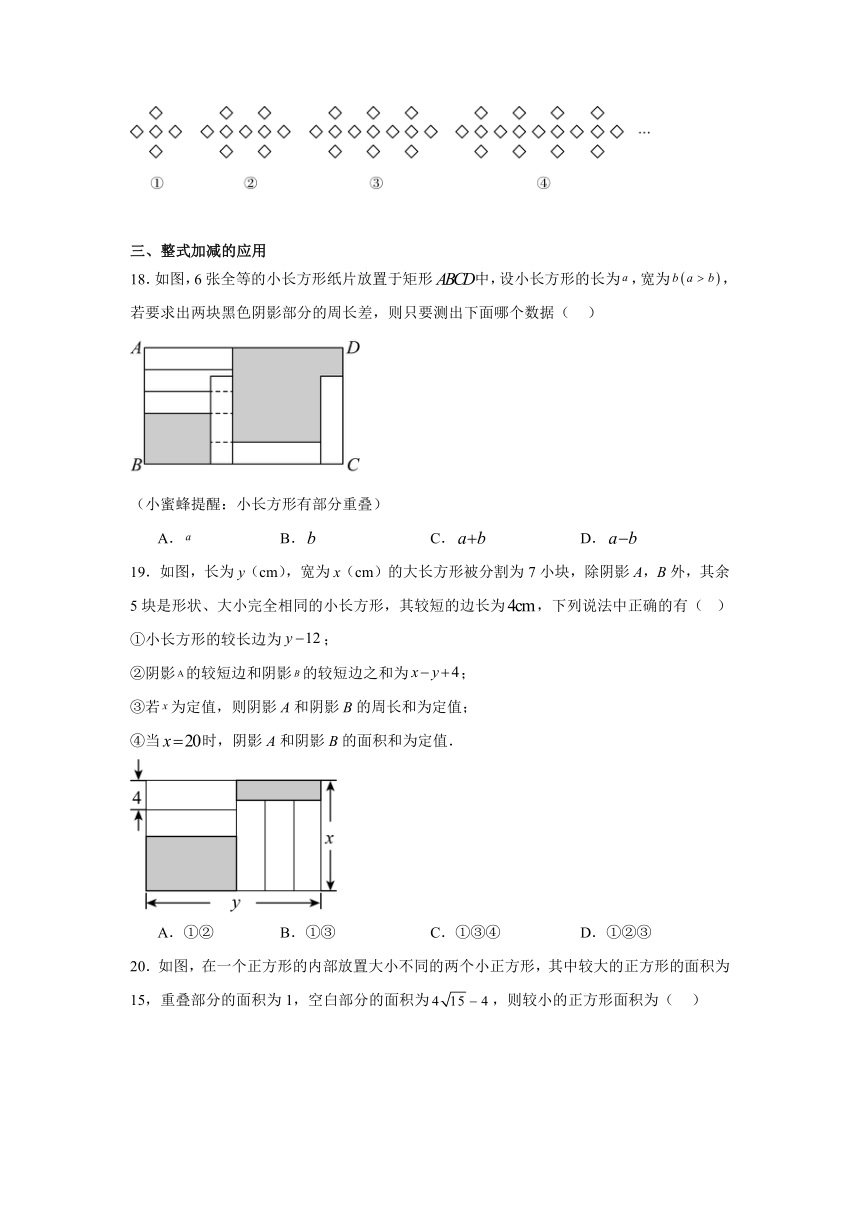
18.如图,6张全等的小长方形纸片放置于矩形中,设小长方形的长为,宽为,若要求出两块黑色阴影部分的周长差,则只要测出下面哪个数据( )
(小蜜蜂提醒:小长方形有部分重叠)
A. B. C. D.
19.如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为,下列说法中正确的有( )
①小长方形的较长边为;
②阴影的较短边和阴影的较短边之和为;
③若为定值,则阴影A和阴影B的周长和为定值;
④当时,阴影A和阴影B的面积和为定值.
A.①② B.①③ C.①③④ D.①②③
20.如图,在一个正方形的内部放置大小不同的两个小正方形,其中较大的正方形的面积为15,重叠部分的面积为1,空白部分的面积为,则较小的正方形面积为( )
A.4 B. C.9 D.
21.已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形,小明把这2个小长方形按如图所示放置在大长方形中,小明经过推事得知,要求出图中阴影部分的周长之和,只需知道a、b、m、n中的一个量即可,则要知道的那个量是( )
A.a B.b C.m D.n
22.如图1,周长为16的长方形纸片剪成①,②,③,④号正方形和⑤号长方形,并将它们按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为 .
23.如图,5张完全一样的长方形卡片放入一张面积为17的正方形卡片中(卡片不重叠,无缝隙),则未被长方形卡片覆盖的A区域与B区域的周长和为 .
24.现有三种边长分别为3,2,1的正方形卡片(如图1),分别记为Ⅰ,Ⅱ,Ⅲ.还有一个长为a,宽为b的长方形.将Ⅰ,Ⅱ,Ⅲ三张卡片按图2的方式,放置在长方形中,则右上角阴影部分与左下角阴影部分周长的差为 .
四、数轴上两点之间的距离和动点问题
25.一把刻度尺的部分在数轴上的位置摆放如图所示,若刻度尺上的刻度“”和“”分别对应数轴上的和,现将该刻度尺沿数轴向右平移个单位,则刻度尺上对应数轴上的数为 .
26.如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示 2的点重合,再将圆沿着数轴向右滚动,则数轴上表示2023的点与圆周上表示哪个数字的点重合?( )
A.0 B.1 C.2 D.3
27.在数学上,不但可以表示5与之差的绝对值,也可以理解为5与两数在数轴上所对应的两点之间的距离,则使得这样的整数一共有( )个
A.7 B.6 C.5 D.4
28.如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示的点重合,再将圆沿着数轴向右滚动,则圆周上表示数字 的点与数轴上表示2023的点重合.
29.长方形在数轴上的位置如图所示,点B、C对应的数分别为和,.若长方形绕着点C顺时针方向在数轴上翻转,翻转1次后,点D所对应的数为2;绕点D翻转第2次;继续翻转,则翻转2023次后,落在数轴上的两点所对应的数中较大的是 .
30.等边在数轴上的位置如图所示,点A、C对应的数分别为0和,若绕顶点按顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转次后,点B对应的数是 .
31.如图,数轴上的点A表示数,点B表示数3,图形I和图形II都有3个边长为1个单位的正方形组成且底边均落在数轴上,开始时,图形的顶点P与顶点A重合,图形II的顶点Q与点B重合,现图形I以每秒3个单位长度的速度向数轴正方向运动,同时图形II以每秒个单位长度的速度向数轴正方向运动.
(1)点A与点B的距离是__________个单位长度.
(2)经过多少时间后,图形I与图形II并行(点P与点Q重合),并求此时点P表示的数.
(3)在运动过程中,当两个图形重叠部分的面积与未重叠部分的面积之比为时,则点P表示的数是__________(直接写出答案).
32.已知:A,B在数轴上,且满足.点B向右平移个单位得到点C,点C向右平移个单位得到点D,点A,B,C,D对应的数分别为a,b,c,d,.
(1) , .
(2)用含n的代数式表示c和d, , .
(3)定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就称点C是的美好点.有理数a,b,c,d,四个数的积为负数,点C,D中存在的美好点,求n的值.
33.如图,动点A,B同时从表示数1的位置出发沿数轴做匀速运动,已知动点A,B运动速度之比是(速度单位:1个单位长度/秒).若经过4秒,点A运动到点M,点M表示的数为,点B运动到点N,且点N在原点的右侧.
(1)点N表示的数为 ;
(2)若动点A,B分别由M,N两点位置同时开始继续按原速运动,且在数轴上的运动方向不限.
①若A,B两点同向运动,当点A运动到与表示数1的位置相距13个单位长度时,求此时点B表示的数.
②若A,B两点在这段运动过程中有段时间内,点B所表示的数与点A所表示的数的和与差均为非负数,则相应这段时间持续了 秒(直接写出答案).
34.如图,数轴上有A,B两点,A,B之间距离为15,原点O在A,B之间,O到A的距离是O到B的距离的两倍.
(1)点A表示的数为______,点B表示的数为______.
(2)点A、点B和点P(点P初始位置在原点O)同时向左运动,它们的速度分别为1,2,2个单位长度每秒,则经过多少秒,点P到点A与点B的距离相等?
(3)点B沿着数轴移动,每次只允许移动1个单位长度,经过6次移动后,点B与原点O相距1个单位长度.满足条件的点B的移动方法共有多少种?
(4)点A和点B同时沿着数轴移动,两点每次均只允许移动1个单位长度.请判点A和点B经过相同次数的移动后,能否同时到达原点O?如果能,请给出点A和点B各自的移动方法:如果不能,请说明理由.
35.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长(单位长度),慢车长(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点为原点,取向右方向为正方向画数轴,此时快车头在数轴上表示的数是,慢车头在数轴上表示的数是.若快车以4个单位长度/秒的速度向右匀速继续行驶,同时慢车以2个单位长度/秒的速度向左匀速继续行驶,且与互为相反数.
温馨提示:忽略两辆火车的车身及双铁轨的宽度.
(1)求此时刻快车头与慢车头之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头相距6个单位长度?
(3)此时在快车上有一位爱动脑筋的七年级学生乘客,他发现行驶中有一段时间秒钟,他的位置到两列火车头、的距离和加上到两列火车尾、的距离和是一个不变的值(即为定值).你认为学生发现的这一结论是否正确?若正确;求出这个时间的值和这个不变值;若不正确,请说明理由.
36.如图,在数轴上有A,B两点,分别表示的数为a,b,且.点P从A点出发以每秒19个单位长度的速度沿数轴向右匀速运动,当它到达B点后立即以相同的速度返回往A点运动,并持续在A,B两点间往返运动.在点P出发的同时,点Q从B点出发以每秒3个单位长度向左匀速运动,当点Q到达A点时,点P,Q停止运动.
(1)________(填空),并求运动了多长时间后,点P,Q第一次相遇,以及相遇点所表示的数;
(2)点C在数轴上对应的数为81,在数轴上是否存在点M,使,若存在,求出点M对应的数,若不存在,说明理由;
(3)求当点P,Q停止运动时,点P所在的位置表示的数;在整个过程中,点P和点Q一共相遇了多少次?
37.已知数轴上A,B两点对应的数字分别是,4,如果把点A往左移动4个单位长度到达点C.动点P以每秒a个单位长度的速度从点C出发往数轴正方向运动,同时动点Q以每秒b个单位长度的速度从点A出发往数轴正方向运动,且.
(1)点A和点B的距离是______,点C对应的数字是______.
(2)若经过3秒后,点P与点Q重合,求的值.
(3)在运动过程中,
①当点P与点Q的距离是2个单位长度且点P位于点Q的左侧时,则所经过的时间为______.(用含a,b的代数式表示)
②若,,当点P与点Q的距离与点A与点B距离之比为时,求此时点P表示的数.
38.【背景知识】数轴是初中数学学习的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律,例如:若数轴上点A,B分别对应数a,b.则A,B两点之间的距离为.
【问题情境】如图,数轴上点A,B分别对应数a,b.其中.
【综合运用】
(1)当时,线段的长度是__________;
(2)若该数轴上另有一点N对应着数n.
①在(1)的条件下,若点N在点A,B之间,且满足,则数n是__________;
②当,且时,探究a与n之间的数量关系.
39.数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小白在草稿纸上画了一条数轴进行操作探究:
操作一:
(1)折叠纸面,若使1表示的点与-1表示的点重合,则-2表示的点与______表示的点重合;
操作二:
(2)折叠纸面,若使1表示的点与-3表示的点重合,回答以下问题:
①3表示的点与______表示的点重合;
②若数轴上、两点之间距离为7(在的左侧),且、两点经折叠后重合,则、两点表示的数分别是______;
操作三:
(3)在数轴上剪下8个单位长度(从-2到6)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图).若这三条线段的长度之比为,则折痕处对应的点所表示的数可能是______.
40.如图1.在数轴上点M表示的数为m,点N表示的数为n,点M到点N的距离记为.我们规定:的大小用位于右边的点表示的数减去左边的点表示的数表示,即.请用上面的知识解答下面的问题:如图2:在数轴上点A表示数a,点B表示数b,点C表示数c,b是最大的负整数.且a,c满足与互为相反数.
(1) , , ;
(2)若将数轴折叠,使得A点与C点重合,则点B与表示数 的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟后.
①请问:的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
②探究:若点A,C向右运动,点B向左运动,速度保持不变,的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.
41.如图,将两个形状完全相同的长方形,放置在数轴上,它们的长为2,宽为1,C与表示的点重合,F与表示3的点重合.长方形以每秒1个单位长度的速度沿数轴向右运动,同时长方形以每秒2个单位长度的速度沿数轴向左运动.设运动时间为t.
(1)当时,点C表示的数为______,点F表示的数为______.
(2)当点C和点F重合时,求t的值.
(3)在运动过程中,两个长方形会出现重叠部分
①请求出有重叠部分时持续的时间.
②当重叠部分周长是长方形周长的一半时,请直接写出此时点C所表示的数为______.
42.实践与探究
【实践】
求出下列每对数在数轴上对应点之间的距离:
(1)与;
(2)与;
(3)与.
【探案】
结论:数轴上两点之间的距离等于这两个点对应数的差的绝对值.
(1)数轴上表示数与1的两点之间的距离可用符号语言记作______.
(2)的含义是数轴上表示数与______的两点之间的距离;
(3)若,则______.
【应用】
如图,长方形和各有一条边在数轴上,长方形的一条边长为2,长方形的一条边长为1,四个点对应的数分别为.用和分别表示两个长方形的面积,求这两个长方形的面积(用含的代数式表示)并比较它们的大小.
43.如图,点为数轴的原点,点表示的数为,边长为的正方形在数轴上,此时点在点左边,且点与点的距离为.
(1)写出数轴上点表示的数为______.
(2)若正方形以每秒个单位长度的速度沿数轴向右运动,同时点以每秒个单位长度从原点出发沿数轴向右运动.
①当,两点相遇时,请求出此时点在数轴上表示的数.
②在整个运动过程中,当点遇到点时,立即以原速度沿数轴向左运动.若点与点的距离等于点到点的距离,此时在数轴上表示的数为______.(直接写出答案即可)
五、实数与数轴
44.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A、B两点表示的数分别为___________,____________;
(2)请你参照上面的方法:
①把图3中的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长___________.(注:小正方形边长都为1,拼接不重叠也无空隙)
②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及.(图中标出必要线段的长)
六、绝对值的意义
45.已知.
(1)用的代数式表示为______;用的代数式表示为______.
(2)求代数式的值.
(3)均为整数,且,求满足条件的的值.
46.已知点A在数轴上对应的数为,点在数轴上对应的数为,,且,A、之间的距离为或,请回答问题:
(1)请直接写出 , , ;
(2)设点在数轴上对应的数为,且,求的值;
(3)如图,点,,是数轴上的三点,点表示的数为4,点表示的数为,动点表示的数是.
①若,求的值;
②求的最小值,并写出此时整数的值.
47.东东在研究数学问题时遇到一个定义:将三个已经排好顺序数,称为数列,计算,,,将这三个数的最小值称为数列的最佳值.例如,对于数列2,,3,因为,,,所以数列2,,3的最佳值为.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列,2,3的最佳值为;数列3,,2的最佳值为1;….经过研究,东东发现,对于“2,,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为.根据以上材料,回答下列问题:
(1)数列,,1的最佳值为
(2)将“,,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,,这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
48.数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.通过研究数轴,我们发现了许多重要的规律,比如:数轴上点A和点B表示的数为a,b,则A,B两点之间的距离.若点A表示的数a为最大的负整数,点B表示的数b在原点右侧,且绝对值为6,则
(1)点A表示的数a为______,点B表示的数b为______,数轴上A,B两点之间的距离为______;
(2)满足的实数x的值为______;
(3)的最小值为______;
(4)满足的实数x的值为______;
(5)若正实数c满足,则当x的值为______时,取到最小值______.
49.如图,已知数轴上两点A、B对应的数分别为a、b,且.动点P从点B出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒().
(1)写出数轴上点A表示的数为 ,点B表示的数为 ,点P表示的数为______(用含t的式子表示);
(2)动点Q从点A出发,以每秒3个单位长度的速度向左匀速运动,动点M从点B出发,以每秒1个单位长度的速度向右匀速运动,且点P、Q、M同时出发.
①当t为何值时,点P、Q两点到点A的距离相等?
②式子的值不随时间t的变化而变化,求m的值.
50.已知有理数理数、、在数轴上的位置如图:
(1)用“”或“”填空:
__________,__________,__________0.
(2)化简:.
(3)若数轴上存在两点、,,则的值是多少?
51.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长(单位长度),慢车长(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头在数轴上表示的数是,慢车头在数轴上表示的数是.若快车以个单位长度/秒的速度向右匀速继续行驶,同时慢车以个单位长度/秒的速度向左匀速继续行驶,且与互为相反数.
(1)求此时刻快车头与慢车头之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头和相距个单位长度.
(3)此时在快车上有一位爱动脑筋的六年级学生乘客,他发现行驶中有一段时间秒钟,他的位置到两列火车头,的距离和加上到两列火车尾,的距离和是一个不变的值(即为定值).你认为学生发现的这一结论是否正确?若正确,求出这个时间及定值;若不正确,请说明理由.
52.阅读信息:
信息一:的几何意义是x与y两数在数轴上所对应的两点之间的距离.例如的几何意义是3与1两数在数轴上所对应的两点之间的距离.
信息二:对于有理数a,b,n,d,若,则称a和b关于n的“双倍关系值”为d.例如,,则6和3关于1的“双倍关系值”为5.
根据以上信息回答下列问题:
(1)和5关于2的“双倍关系值”为______.
(2)若a和3关于1的“双倍关系值”为4,求a的值;
(3)若和关于1的“双倍关系值”为2,和关于2的“双倍关系值”为2,和关于3的“双倍关系值”为2,…,和关于21的“双倍关系值”为2.
①的最大值为______;
②的值为______(用含的式子表示).
53.数轴上有A、B两点,分别对应的数为a,b,已知与互为相反数.点为数轴上一动点,对应的数为x.
(1)若点P到点A和点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A和点B的距离之和为10?若存在,请求出x的值;若不存在,说明理由;
(3)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,点B以每分钟20个单位长度的速度向左运动,问几分钟时点P到点A、点B的距离相等?
54.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为.在数轴上A、B两点之间的距离.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是______,数轴上表示2和的两点之间的距离为______.
(2)数轴上表示x和两点之间的距离为______,若x表示一个有理数,且,则______.
(3)利用数轴求出的最小值为______,并写出此时x可取哪些整数值______.
参考答案:
题号 1 2 3 4 13 14 15 18 19 20
答案 B A D B A A B B C C
题号 21 26 27
答案 D B A
1.B
【难度】0.65
【分析】本题考查数字规律探究.
根据数字规律表可知,偶数行为负数,奇数行为正数;第二行的数是第一行数正序对应数的倍,第三行的数是第一行数反序后对应数的倍,第四行的数是第一行数反序后对应数的倍,第五行的数是第一行对应数的倍,,则第一行从第一行到第四行的排序方式是正序、正序、反序、反序的方式循环;第行就是倍,偶数行时为,奇数行时为;按此规律列出所以可能情况即可判断.
【详解】解:根据题意,当在第6行时,△在第7行,数字为第一行反序后对应数的倍,即为;
当在第8行时, △在第9行,数字为第一行数正序对应数的倍,即为;
当在第12行时, △在第13行,数字为第一行数正序对应数的倍,即为;
当在第24行时, △在第25行,数字为第一行数正序对应数的倍,即为;
综上所述,可能出现的数字为:,
∴不可能出现的数字是50,
故答案为:B.
2.A
【难度】0.65
【分析】本题考查了数字类变化规律,根据题意计算归纳得出若的所有正约数为,,…,,则,再结合,得出,即可得出答案,得出规律是解此题的关键.
【详解】解:对于的个正约数1,,,有,
对于的个正约数,,,有,
对于的个正约数,,,,,有,
对于的个正约数,,,有,
对于的个正约数,,,,,,,,,有,
…,
若的所有正约数为,,…,,则,
,
,
当时,,
故选:A.
3.D
【难度】0.65
【分析】本题主要考查了有理数混合运算,解题的关键是根据题意得出,求出即可得出答案.
【详解】解:
,
设,
则,
∴,
解得:,
∴,
即.
故选:D.
4.B
【难度】0.85
【分析】此题主要考查了数字的规律知识,得出第一列的奇数行的数的规律与第一行的偶数列的数的规律是解决问题的关键.
根据已知数据可得出第一列的奇数行的数的规律是第几行就是那个数平方,同理可得出第一行的偶数列的数的规律,从而得出2023所在的位置.
【详解】解:由已知可得:根据第一列的奇数行的数的规律是第几行就是那个数平方,第一行的偶数列的数的规律,与奇数行规律相同;
∵,在第45行,
∵向右依次减小,
∴2023所在的位置是第45行,第3列,
∴其有序数对.
故选:B.
5.301
【难度】0.4
【分析】本题考查了无理数的估算,掌握算术平方根的意义及新定义的意义是解题的关键;根据的意义,对每个无理数进行估算即可.
【详解】解:当时,;当时,;当时,;当时,;当时,;当时,;当时,;
∴
.
故答案为:301.
6.
【难度】0.65
【分析】本题考查数字变化的规律,解题的关键是能根据题意依次求出,,,,,及熟知(为正整数).据此解答即可.
【详解】解:由题意得:
,
,
,
∴,
∴(为正整数),
∴
.
故答案为:.
7.
【难度】0.4
【分析】根据题意,先求出这列数的前几项,从而得出这个数列以-2,,依次循环,且-2++=-,再求出这100个数中有多少个循环组,从而得出答案.
【详解】解:∵a1=-2,
,
,
,
……
∴这个数列以-2,,依次循环,且-2++=-,
∵100÷3=33…1,
∴a1+a2+…+a100=33×(-)-2=-.
故答案为:-.
【点睛】本题是对数字变化规律的考查,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.
8.
【难度】0.65
【分析】本题考查了数字的规律变化,通过观察数字,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键.根据题意易得,, ,,…,由此可得该组数是4个一循环,进而问题可求解.
【详解】解∶∵,是的“牛顿数”,
∴,
∵是的“牛顿数”,
∴,
∵是的“牛顿数”,
∴,
∵是的“牛顿数”,
∴,
…,
∴,,,四个一循环,
∵,
∴.
故答案为:.
9. 3 6
【难度】0.65
【分析】本题考查了古籍数学的认识和应用,设的十位数是m,个位数是n,根据“铺地毯”法则,建立等式计算即可.
【详解】设的十位数是m,个位数是n,
根据题意,如图,
∴,
∴,
∴,
∴,
故答案为:3, 6.
10.12
【难度】0.65
【分析】本题考查的是图形的变化规律,关键是通过图1中面积为10的阴影正方形,分析出图2中面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;然后列式求解即可.
图1中阴影正方形的面积为10,被全部覆盖的小方格有4个,被部分覆盖的小方格有10个;则面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为、、、、、、、;因,将式子进行化简计算即可.
【详解】解:如图所示,
面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;
被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为;
因为,即,
,
解得:.
故答案为:12.
11.
【难度】0.65
【分析】本题考查了一元一次方程的应用.根据“使6条边上四个数之和都相等”列方程求解.
【详解】解:设右下边为x,由满足6条边上四个数之和都相等,他们的和为,如图所示:
观察图形还有,,,2,3,5六个数字,
观察“六角幻星”图可知与相差6,只有,5或2,满足,
则或,
解得:或(不合题意,舍去),
故答案为:.
12.
【难度】0.65
【分析】(1)结合图形观察数字,发现:,,进一步得到;
(2)在计算的时候,根据,…进行简便计算.
【详解】,
,
,
,
,
∴,
,
故答案为:;.
【点睛】此题考查了图形的变化规律题,找到规律,利用分数的加减法进行简便计算是解题的关键.
13.A
【难度】0.85
【分析】此题考查图形的变化规律.由图可知:则第n个图形需要黑色棋子的个数是.由此代入求得答案即可.
【详解】解:∵第1个图形需要黑色棋子的个数是,
第2个图形需要黑色棋子的个数是,
第3个图形需要黑色棋子的个数是,
…,
∴第n个图形需要黑色棋子的个数是;
则第10个图形需要黑色棋子的个数是.
故选:A.
14.A
【难度】0.65
【分析】根据题意分别求出电子跳蚤每次跳后的位置,从而得到点P6与点P4重合,然后用2014除以6,根据余数是4可得P2014与P4重合,从而得解.
【详解】解:∵BC=10,BP0=4,
∴CP0=6,
第一步:CP1=CP0=6,
∵AC=9,
∴AP1=9-6=3,
第二步:AP2=AP1=3,
∵AB=8,
∴BP2=5,
第三步:BP3=BP2=5,
依此类推,第四步,CP4=CP3=5,
第五步,AP5=AP4=4,
第六步,BP6=BP5=4,
此时P6与P0重合,即经过6次跳,电子跳蚤回到起跳点,
∵2014÷6=335余4,
∴P2014是第336循环组的第4步,与P4重合,
此时P4与P2014之间的距离是0.
故选:A.
【点睛】本题是对图形变化规律的考查,读懂题目信息求出各步跳动后的位置,并且得到经过6次跳,电子跳蚤回到起跳点是解题的关键.
15.B
【难度】0.85
【分析】总结规律第个图形中所用正方形卡片比等边三角形卡片多几枚,当时,求出所用正方形卡片及等边三角形卡片的数量,栽求和即可得到答案.
【详解】解:第1个图形中所用正方形卡片比等边三角形卡片多(枚),
第2个图形中所用正方形卡片比等边三角形卡片多(枚),
第3个图形中所用正方形卡片比等边三角形卡片多(枚),
第个图形中所用正方形卡片比等边三角形卡片多(枚),
当时,所用正方形卡片为:(枚),所用等边三角形卡片为:,
所用两种卡片的总数为:(枚),
故选:B.
【点睛】本题考查了与有理数有关的规律探究,解题的关键是总结规律第个图形中所用正方形卡片比等边三角形卡片多几枚.
16.56
【难度】0.85
【分析】本题主要考查了图形规律探索,一元一次方程的应用,解题的关键是根据图形得出规律,先求出拼成图1所示的47个边长为1的正方形,需要的火柴棒的根数为142根,设这些火柴按如图2所示的方式拼,可以拼成的正方形个数为x个,根据图形规律列出方程,解方程即可.
【详解】解:拼成图1所示的47个边长为1的正方形,则需要的火柴棒的根数为:
(根),
设这些火柴按如图2所示的方式拼,可以拼成的正方形个数为x个,根据题意得:
,
解得:,
即可以拼出56个边长为1的正方形.
故答案为:56.
17.
【难度】0.85
【分析】根据图形变化的规律得出第个图形中有个正方形即可解答
【详解】解:由题知,第①个图案中有个正方形,第②个图案中有个正方形,第③个图案中有个正方形,第④个图案中有个正方形,…,第n个图案中有个正方形,
∴第⑨个图案中正方形的个数为,
故答案为:.
【点睛】本题考查了图形的变化规律,根据图形的变化得出第个图形中有个正方形是解题的关键.
18.B
【难度】0.65
【分析】本题考查整式加减的应用,准确识图,利用平移思想分析得出两块阴影部分的周长之差即为长方形和长方形的周长之差是解题关键.延长交于点K,根据图形得出,,,,根据题意得出,两块阴影部分的周长差为:,然后去括号,合并同类项得出结果,作出判断即可.
【详解】解:延长交于点K,如图所示:
由题意可得:,,,,
结合平移思想可得两块阴影部分的周长之差即为长方形和长方形的周长之差,
两块阴影部分的周长差为:
,
若要求出两块黑色阴影部分的周长差,则只要测出数据b,
故选:B.
19.C
【难度】0.65
【分析】先根据图形即题目给出的数据得出阴影A、阴影B和5个小长方形的较长边和较短边,分别按照①②③④的要求进行计算即可.
【详解】解:由题可知,阴影A的较长边为,较短边为;
阴影B的较长边为12,较短边为;
小长方形的较长边为,较短边为4,
则①小长方形的较长边为,故①正确;
②阴影A的较短边和阴影B的较短边之和为,故②错误;
③阴影A和阴影B的周长和为,若x为定值,则阴影A和阴影B的周长和为定值,故③正确;
④阴影A和阴影B的面积和为,当时,阴影A和阴影B的面积和为240,是一个定值,故④正确.
综上可知,正确的为①③④.
故答案选C.
【点睛】本题考查了整式加减的运用,准确计算是解题关键.
20.C
【难度】0.85
【分析】本题主要考查了二次根式的应用,观察图形得到各个正方形边长之间的关系是解题的关键.根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
【详解】解:∵观察可知,两个空白部分的长相等,宽也相等,
∴重叠部分也为正方形,
∵空白部分的面积为,
∴一个空白长方形面积为,
∵大正方形面积为15,重叠部分面积为1,
∴大正方形边长为,重叠部分边长1,
∴空白部分的长为,
设空白部分宽为x,可得:,解得:,
∴小正方形的边长=空白部分的宽+重叠部分边长,
∴小正方形面积,
故选:C.
21.D
【难度】0.94
【分析】先用含a、b、m、n的代数式表示出阴影矩形的长宽,再求阴影矩形的周长和即可.
【详解】解:如图,由图和已知条件可知:AB=a,EF=b,AC=n﹣b,GE=n﹣a.
阴影部分的周长为:2(AB+AC)+2(GE+EF)
=2(a+n﹣b)+2(n﹣a+b)
=2a+2n﹣2b+2n﹣2a+2b
=4n.
∴求图中阴影部分的周长之和,只需知道n一个量即可.
故选:D.
【点睛】本题主要考查了整式的加减,能用含a、b、m、n的代数式表示出阴影矩形的长宽是解决本题的关键.
22.
【难度】0.65
【分析】本题考查整式加减法与几何图形的应用,巧妙设未知数,列出代数式表示各个图形的边长,利用整体思想求值是解答的关键.
在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,根据图1的周长求得,再根据图2的周长求得,进而可由没有覆盖的阴影部分的周长为求解即可.
【详解】解:在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,
由图1中长方形的周长为16得,
解得:,
如图2,
由图2中的长方形的周长为40得,
∴,
由图2得没有覆盖的阴影部分的周长为,
故答案为:36.
23.
【难度】0.65
【分析】本题考查整式的加减运算的应用,算术平方根的应用.
设长方形的长为a,宽为b. 根据正方形的面积求得a,b,然后根据图中等量关系列代数式求值即可.
【详解】解:设长方形的长为a,宽为b.
因为面积为17的正方形卡片可知,,
解得:,,
所以未被长方形卡片覆盖的A区域与B区域的周长和为:
.
故答案为:.
24.4
【难度】0.85
【分析】本题考查了整式的加减的应用,根据周长的定义列出代数式计算即可得出答案,采用数形结合的思想是解此题的关键.
【详解】解:由图可得:
周长之差为:
,
故答案为:.
25.
【难度】0.65
【分析】通过两点间的距离比求出数轴上刻度“”与刻度“”之间的距离,进而求刻度“”在数轴对应的数及符号,最后通过“左加右减”即可求解.
本题主要考查了数轴与刻度尺,解题关键是求出一个单位长度代表多少厘米.
【详解】解:因为刻度尺上的刻度“”和“”分别对应数轴上的和,
∴刻度尺上刻度“”与刻度“”之间的距离是,是刻度尺上刻度“”与刻度“”之间的距离的倍;
而数轴上刻度“”和“”之间的数轴距离是,
所以数轴上刻度“”与刻度“”之间的距离是,由于刻度“”在数轴的左边,属于负数,所以对应的数应为,向右平移个单位后为.
故刻度尺上对应数轴上的数为.
故答案为:.
26.B
【难度】0.85
【分析】本题考查数轴,有理数的减法与除法,圆周上表示数字0的点与数轴上表示的点重合,滚动到2023时,滚动了2025个单位长度,用2025除以4,余数即为重合点.
【详解】解:圆周上表示数字0的点与数轴上表示的点重合,
,
,
∴数轴上表示2023的点与圆周上表示1的点重合.
故选:B.
27.A
【难度】0.85
【分析】本题考查了数轴,绝对值等知识.理解为:数对应的点到两数1与两数在数轴上所对应的两点之间的距离之和为6.所以数对应的点在1到之间,整数有7个.
【详解】解:.
,
,,,,,0,1共7个整数.
故答案为:A.
28.0
【难度】0.85
【分析】圆周上的0点与重合,滚动到2023,圆滚动了2024个单位长度,用2024除以4,余数即为重合点.
【详解】解:圆周上的0点与重合,
,
,
圆滚动了506 周到2023,
圆周上的0与数轴上的2023重合,
故答案为:0.
【点睛】本题考查了数轴,找出圆运动的规律与数轴上的数字的对应关系是解决此类题目的关键.
29.
【难度】0.65
【分析】本题考查了数轴的应用,解题的关键是找出题目中的规律,根据发现的规律可以计算出数轴上对应的数.由题意知,每4次翻转为一个循环组依次循环,且矩形周长为8,计算2023被4除的余数即可求得答案.
【详解】解:由题意得:
第一次翻转,右边的点移动3个单位,
第二次翻转,右边的点移动1个单位,
第三次翻转,右边的点移动3个单位,
第四次翻转,右边的点移动1个单位,
翻转4次,为一个周期,
一个周期,右边的点移动8个单位,
,
右边的点移动,
,
故答案为:.
30.
【难度】0.85
【分析】先确定,翻转1次后,点B所对应的数为1;翻转4次后,点B所对应的数为;翻转7次后,点B所对应的数为,由于,从而可判断连续翻转次后,点B对应的数为.
【详解】解:∵点A、C对应的数分别为0和,
∴,
∵为等边三角形,
∴,
∵绕顶点按顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,翻转3次后,点B所对应的数为3,翻转4次后,点B所对应的数为;翻转7次后,点B所对应的数为,
而,
∴连续翻转次后,点B对应的数为.
故答案为:.
【点睛】本题考查了数轴:所有的有理数都可以用数轴上的点表示.也考查了等边三角形的定义和数字变换规律型问题的解决方法.
31.(1)8
(2)经过秒后,图形I与图形II并行(点P与点Q重合),此时点P表示的数为
(3)或
【难度】0.65
【分析】本题考查了数轴,一元一次方程的应用;
(1)根据数轴上两点间距离的求法计算即可;
(2)设运动时间为t,根据点P与点Q重合时表示的数相同,列方程求出时间t,进而可计算此时点P表示的数;
(3)由题意可知重叠部分为1个正方形,设运动时间为t,分情况讨论:当点P在点Q左侧时;当点P在点Q右侧时;分别根据重叠部分为1个正方形,列方程求出时间t,进而可计算此时点P表示的数.
【详解】(1)解:∵点A表示数,点B表示数3,
∴点A与点B的距离是,
故答案为:8;
(2)设运动时间为t,
由题意得:,
解得:,
此时点P表示的数为,
答:经过秒后,图形I与图形II并行(点P与点Q重合),此时点P表示的数为;
(3)∵重叠部分的面积与未重叠部分的面积之比为,
∴重叠部分为1个正方形,
设运动时间为t,
当点P在点Q左侧时,
由题意得:,
解得:,
此时点P表示的数为;
当点P在点Q右侧时,
由题意得:,
解得:
此时点P表示的数为:;
故答案为:或.
32.(1),
(2),
(3)
【难度】0.65
【分析】本题考查绝对值和算术平方根的非负性,数轴,一元一次方程的应用.
(1)根据绝对值和算术平方根的非负性求解即可;
(2)根据数轴上的点平移的变化规律即可解答;
(3)分两种情况讨论:点C是的美好点或点D是的美好点.根据“美好点”的定义列出方程,求解后结合进行取舍,即可解答.
【详解】(1)解:∵,,
且,
∴,,
∴,,
∴,;
故答案为:,
(2)解:∵点B表示的数是,向右平移个单位得到点C,
∴点C表示的数是,即,
∵点C向右平移个单位得到点D,
∴点D表示的数是,即.
故答案为:,
(3)解:若点C是的美好点,
则
解得:,
∴,,
∴,不合题意,舍去;
若点D是的美好点,
则
解得:,
∴,,
∴,符合题意.
综上所述,.
33.(1)5
(2)①或;②或1
【难度】0.65
【分析】此题考查了一元一次方程的实际应用-行程问题;有理数在数轴上的表示,数形结合和列出一元一次方程是解题的关键.
(1)先求点A的运动速度,然后根据点A,B的运动速度之比求点B的运动速度,进而得到点N的表示的数.
(2)①分两种情况:当 A,B两点向左运动时;当A,B两点向右运动时, 然后分别求点B表示的数.
②设运动t秒,根据点B所表示的数与点A所表示的数的和与差均为非负数,分两种情况:当 A,B两点向右运动时,点A所表示的数为,点B所表示的数为;当A点向右,B点向左运动时,点A所表示的数为,点B所表示的数为,然后列等式求解即可.
【详解】(1)解:∵点A从数1的位置经过4秒运动到点M, 点M表示的数为,
∴点A的运动速度为
∵点A,B的运动速度之比是,
∴点B的运动速度为1.
所以点N的表示的数为.
故答案为:5.
(2)①分两种情况:
当 A,B两点向左运动时, 点B表示的数为;
当A,B两点向右运动时, 点B表示的数为.
综上所述, 点B表示的数为或.
②设运动t秒,根据点B所表示的数与点A所表示的数的和与差均为非负数,分两种情况:
当 A,B两点向右运动时,点A所表示的数为,点B所表示的数为
所以,解得 .
,解得.
所以相应这段时间持续了秒 ;
当A点向右,B点向左运动时,点A所表示的数为,点B所表示的数为
所以,解得.
. 解得
所以相应这段时间持续了秒 .
综上所述, 这段时间持续了或1秒 .
34.(1);
(2)经过5或15秒,点P到点A与点B的距离相等;
(3)有7种移动方法;
(4)A和点B经过相同次数的移动后,不能同时到达原点O
【难度】0.4
【分析】(1)设,则,根据“A,B之间距离为15“列方程,可求出x,进而得到点A表示的数,点B表示的数;
(2)设经过t秒,点P到点A与点B的距离相等,列方程求解即可;
(3)设点B沿着数轴向左移动次,则向右移动次,可得,再分析即可;
(4)设点A向左移动次,向右移动次,则B移动次,可得:,设B向左移动次,向右移动了次,可得,结合移动次数为非负整数可得答案.
【详解】(1)解:设点B表示的数为x,则点A表示的数为,
则,
解得:,
∴点A表示的数为,点B表示的数为;
(2)设经过t秒,A对应的数为,P对应的数为,B对应的数为,而点P到点A与点B的距离相等,
则:即,
解得:或,
答:经过5或15秒,点P到点A与点B的距离相等;
(3)设点B沿着数轴向左移动次,则向右移动次,
∴,即,
解得:或,
当时,有1种移动方法,
当时,移动方式有左5(连续)右1,左4(连续)右1左1,左3(连续)右1左2(连续),左2(连续)右1左3(连续),左1右1左4(连续),右1左5(连续),
综上共有7种移动方法;
(4)不能,理由如下:
设点A向左移动次,向右移动次,则B移动次
∴,
解得:,
设B向左移动次,向右移动了次,
∴,
∴
∵,,都为正整数,
∴不符合题意,
∴A和点B经过相同次数的移动后,不能同时到达原点O.
【点睛】本题考查的是数轴上两点之间的距离,数轴上的动点问题,一元一次方程的应用,本题难度大,熟练的利用一元一次方程解题是关键.
35.(1);
(2)再行驶3秒或5秒钟两列火车行驶到车头相距6个单位长度;
(3)这个时间为秒,定值为6个单位.
【难度】0.65
【分析】(1)由题意可得,求出,即可求解;
(2)分两种情况,点在点的右侧或点在点的左侧,分别求解即可;
(3)由题意可得当在之间时,为定值,据此求解即可.
【详解】(1)解:由题意可得
∴,,解得,
即点表示的数为,点表示的数为,
之间的距离为;
(2)设经过秒钟,相距为6个单位,此时点表示的数为,点表示的数为,
当点在点的右侧,,解得
当在点的左侧时,,解得
即再行驶3秒或5秒钟两列火车行驶到车头相距6个单位长度;
(3)由题意可得,在线段上
∴
由为定值可得,为定值,
所以此时点在线段上,,
时间
即这个时间为秒,定值为6个单位.
【点睛】本题考查了两点的距离,数轴,绝对值和偶次方的非负性,知道数轴上任意两点之间的距离等于右边的数减去左边的数,熟练掌握行程问题的数量关系,时间等于路程除以速度,根据数形结合的思想理解和解决问题.
36.(1)132;6;61
(2)存在点M,使,点M对应的数为或
(3)当点P,Q停止运动时,点P所在的位置表示的数为,点P和点Q一共相遇了次
【难度】0.4
【分析】本题考查了数轴上的动点问题,数轴上两点间距离;
(1)根据可得,故可得的长度,再利用时间等于路程除以速度和,即可解答;再根据求得时间,即可得到相遇点表示的数;
(2)设点表示的数为,考虑两种情况,即点在点左边,点在点和点中间,再根据,列方程即可解答;
(3)求出点运动的时间,即可算出点运动的路程,再求出点的位置即可,再根据点来回次数,求得和点相遇次数.
熟练利用代数式表示动点表示的位置是解题的关键.
【详解】(1)解:根据,可得,,
,
(秒),
相遇的点为;
(2)解:设点表示的数为,
①当点在点左边时,
,,,
根据,可列方程,
解得;
②点在点和点中间时,
,,,
根据,可列方程,
解得;
综上所述,存在点M,使,点M对应的数为或;
(3)解:点运动的时间为(秒),
,
所以可得点总共往返6趟,且最后停止在处,
综上所述,点P和点Q一共相遇了7次.
37.(1)6;
(2)
(3)①;②;8
【难度】0.65
【分析】(1)根据数轴上两点间距离公式进行解答即可;
(2)①根据时间进行计算即可;
②设运动时间为,则运动后,点P表示的数为:,点Q表示的数,分两种情况:Q在P右侧时,Q在P左侧时,列出方程,求出t的值即可.
【详解】(1)解:点A和点B的距离是:;
点C对应的数是;
故答案为:6;.
(2)解:∵的距离长度为4,
∴速度差,
∴.
(3)解:①的距离为6,则的距离为2,的距离长度为4.
Q在P左侧时,时间秒;
故答案为:.
②∵点P与点Q的距离与点A与点B距离之比为,
∴此时,
∵,,
∴设运动时间为,则运动后,点P表示的数为:,点Q表示的数,
(i)Q在P右侧时,,
解得:,
则P点对应的数为.
(ii)Q在P左侧时,,
解得:,
则P点对应的数为.
综上分析可知,点P表示的数为或8.
【点睛】本题主要考查了数轴上两点间的距离,用数轴上点表示有理数,数轴上动点问题,一元一次方程的应用,解题的关键是熟练掌握数轴上两点间距离,注意分类讨论.
38.(1)10
(2)①;②或.
【难度】0.85
【分析】本题考查了数轴上两点之间的距离、一元一次方程、合并同类项.
(1)根据两点之间的距离公式计算即可;
(2)①根据两点之间的距离公式,得出,,再根据,列出一元一次方程,解出即可得出答案;
②根据题意,列出方程整理即可得出结论.
【详解】(1)解:∵当,时,
∴线段;
故答案为:10;
(2)解:①∵数轴上另有一点N对应着数n,点N在点A,B之间,,,
∴,,
又∵,
∴,
解得:,
∴数n是;
故答案为:;
②∵,
∴,
整理得或,
即或.
39.(1)2;(2)①-5,②-4.5和2.5;(3)1或2或3
【难度】0.65
【分析】(1)利用数轴的对称性可得答案;
(2)①先确定好折痕点对应的数,再利用距离相等可得答案;②利用数轴上、两点到折痕的距离为3.5,从而可得答案;
(3)分三种情况画出符合题意的图形,再利用对折的性质,逐一解答即可.
【详解】解:操作一,
(1)∵表示的点1与-1表示的点重合,
∴折痕为原点,
则-2表示的点与2表示的点重合,
故答案为:2;
操作二:
(2)∵折叠纸面,若使1表示的点与-3表示的点重合,
则折痕表示的点为-1,
①设3表示的点与数表示的点重合,
则,
则;
②∵数轴上、两点之间距离为7,
∴数轴上、两点到折痕-1的距离为3.5,
∵在的左侧,
则、两点表示的数分别是-4.5和2.5;
故答案为:①-5,②-4.5和2.5;
操作三:
(3)如图1,当时,
设,,,
,
则,
∴,,,
∴折痕处对应的点所表示的数是:,
如图2,当时,
设,,,
,
则,
∴,,,
∴折痕处对应的点所表示的数是:,
如图3,当时,
设,,,
,
则,
∴,,
∴折痕处对应的点所表示的数是:,
综上所述:则折痕处对应的点所表示的数可能是1或2或3.
故答案为:1或2或3.
【点睛】本题考查了实数和数轴的关系,及数轴上的折叠变换问题,明确①数轴上折叠后重合的点到折痕的距离相等,②数轴上任意两点的距离为两点坐标的绝对值;本题第三问有难度,采用了分类讨论的思想.
40.(1),,5
(2)3
(3)①28;②当时,的值随时间t的变化而变化;当时,的值为26.
【难度】0.4
【分析】(1)根据最大的负整数是 1,绝对值和偶次方具有非负性可求解;
(2)由题意容易得出折叠点表示的数是1,再根据与2的距离可得答案;
(3)①先表示出t秒后A、B、C表示的数,然后分别求出,,再代入计算即可得出结论;
②先表示出t秒后A、B、C表示的数,然后分别求出,,然后分A在B的左侧;A在B的右侧讨论,再代入计算即可得出结论.
【详解】(1)解:∵a,c满足与互为相反数,
∴,
∴,,
∴,,
∵b是最大的负整数,
∴;
故答案为:,,5;
(2)解:当与5重合时,折叠点是,
∴与点B重合的点表示的数为:,
故答案为:3;
(3)解:①t秒后,A表示的数为,B表示的数为,C表示的数,
∴,
,
∴
;
②秒后,A表示的数为,B表示的数为,C表示的数,
∴,
,
当A、B重合时,,解得,
当A在B的左侧,即时,,
∴
,
∴的值随时间t的变化而变化;
当A在B的右侧,即时,,
∴
;
综上,当时,的值随时间t的变化而变化;当时,的值为26.
41.(1),1
(2)的值为3
(3)①有重叠部分时持续的时间为1秒;②或
【难度】0.4
【分析】本题考查数轴上点的运动,一元一次方程的应用,解题关键是表示出运动后点表示的数.
(1)当时,根据路程速度时间及数轴上两点之间的距离即可求解;
(2)根据题意,可得点表示的数为,点表示的数为,再由点和点重合,建立方程求解即可得出答案;
(3)①分别求得点与点重合、点与点重合所需时间,求出两个时间差即可;②分两种情况:当点落在线段上时,当点落在线段上时,分别画出图形,根据题意建立方程求解即可得出答案.
【详解】(1)解:当时,点表示的数为,点表示的数为,
(2)由题意得:秒后,点表示的数为:,点表示的数为:,
∵点和点重合,
∴,
解得:,
∴的值为3;
(3)①由题意得:秒后,点表示的数为:,点表示的数为:,
当点与点重合时:,
解得:,
由(2)知:时,点与点重合,
∵(秒),
∴有重叠部分时持续的时间为1秒;
②当点落在线段上时,如图,
∵重叠部分长方形的周长是长方形的周长的一半,
∴,
∵,,,
∴,
解得:,
∴点所表示的数为;
当点落在线段上时,如图,
∵重叠部分长方形的周长是长方形的周长的一半,
∴,
∵,,,
∴,
解得:,
∴点所表示的数为;
综上所述,点所表示的数为或;
42.实践:(1);(2);(3)6;探案:(1);(2);(3)1或;应用:,;
【难度】0.65
【分析】实践:根据数轴上两点间距离公式进行求解即可;
探案:(1)根据数轴上两点间距离计算方法进行表示即可;
(2)根据绝对值的意义和数轴上两点间距离公式进行解答即可;
(3)解绝对值方程求出结果即可;
应用:根据数轴上两点距离公式和长方形面积公式求出和,然后进行比较大小即可.
【详解】解:实践:(1);
(2);
(3);
探案:(1)数轴上表示数与1的两点之间的距离可用符号语言记作;
故答案为:;
(2)的含义是数轴上表示数与的两点之间的距离;
故答案为:;
(3)∵,
∴,
解得:或;
故答案为:1或;
应用:,
,
∴
,
根据数轴可知,,
∴,
∴,
∴.
【点睛】本题主要考查了数轴上两点间距离,绝对值的意义,整式加减的应用,绝对值方程,数轴上点的特点,解题的关键是熟练掌握相关的知识,数形结合.
43.(1)
(2)①点在数轴上表示的数为;②或
【难度】0.4
【分析】(1)根据点表示的数和点与点的位置关系和距离求出点表示的数,再根据正方形的边长即可求出数轴上点表示的数;
(2)①根据点和点之间的距离以及运动速度求出两点相遇时的运动时间,即可求出相遇时点表示的数,再加上正方形的边长即可求出相遇时点在数轴上表示的数;
②由①可知相遇时点在数轴上表示的数,然后根据条件列出方程,求出满足条件时的运动时间,再根据运动时间即可求出点在数轴上表示的数.
【详解】(1)解:∵点表示的数为,点在点左边,且点与点的距离为;
∴点表示的数为:,
∵边长为的正方形在数轴上,
∴点在点左边,,
∴点表示的数为:,
故答案为:;
(2)①设P、B两点相遇时间为秒,
由题意得:,
解得:,
此时点表示的数为:,
∴相遇时点表示的数为:;
②由①可知:相遇时、表示的数为,点表示的数为,
即点与点重合,
设相遇后的运动时间为秒,
当点与点的距离等于点到点的距离时,,,
∴,
解得:或,
∴当时,点表示的数为:,
当时,点表示的数为:,
综上所述,此时在数轴上表示的数为或.
故答案为:或.
【点睛】本题考查用数轴上的点表示数,数轴上的动点问题,数轴上两点之间的距离,一元一次方程的应用,路程与速度之间的关系等知识点,正确理解题意并建立一元一次方程是解题的关键.
44.(1),;(2)①图见解析,;②见解析
【难度】0.4
【分析】(1)根据图1得到小正方形的对角线长,即可得出数轴上点A和点B表示的数
(2)根据长方形的面积得正方形的面积,即可得到正方形的边长,再画出图象即可;
(3)从原点开始画一个长是2,高是1的长方形,对角线长即是a,再用圆规以这个长度画弧,交数轴于点M,再把这个长方形向左平移3个单位,用同样的方法得到点N.
【详解】(1)由图1知,小正方形的对角线长是,
∴图2中点A表示的数是,点B表示的数是,
故答案是:,;
(2)①长方形的面积是5,拼成的正方形的面积也应该是5,
∴正方形的边长是,
如图所示:
故答案是:;
②如图所示:
【点睛】本题考查无理数的表示方法,解题的关键是理解题意,模仿题目中给出的解题方法进行求解.
45.(1);
(2)
(3),,,
【难度】0.65
【分析】此题主要考查了代数式求值,等式性质,绝对值的意义,解题的关键是掌握整体代入的思想.
(1)根据等式的性质即可求解;
(2)将原式变形,进而将已知代入求出即可;
(3)根据,得出,,再根据均为整数,即可求解.
【详解】(1)解:∵,
∴用的代数式表示为,
用的代数式表示为.
故答案为:;.
(2)解:,
.
(3)解:∵,
∴,,
,均为整数,,
∴,,,.
46.(1);2;5
(2)10或0
(3)①或;②,0,1,2,3,4
【难度】0.85
【分析】(1)先根据绝对值的非负性求出a、b的值,再根据两点间的距离公式求解;
(2)分类讨论解方程即可;
(3)①先根据x的范围去掉绝对值符号,再解方程即可;
②根据点M、点N之间时,最小,求出此时整数的值即可.
【详解】(1)解:∵,
∴,
∴A、B间的距离为,
故答案为:;
(2)解:
当时,,则;
当时,,则;
10或0.
(3)解:①当点在点左侧时,,
∴,
;
当点在点右侧时,,
,
∴,
;
综上所述,或.
②当点在点、之间时,,
的最小值为;
此时,,0,1,2,3,4.
【点睛】本题考查的是数轴上两点之间的距离,一元一次方程的应用,绝对值方程,数轴上点表示有理数,利用数形结合,方程思想解决问题是解本题的关键.
47.(1)3
(2);,2,或2,,
(3)11或4或10
【难度】0.65
【分析】(1)根据上述材料给出的方法计算其相应的最佳值为即可;
(2)按照三个数不同的顺序排列算出最佳值,由计算可以看出,要求得这些数列的最佳值的最小值;只有当前两个数的和的绝对值最小,最小只能为,由此得出答案即可;
(3)分情况算出对应的数值,建立方程求得a的数值即可.
【详解】(1)因为,,,
所以数列,,1的最佳值为3.
故答案为3.
(2)对于数列,,2,
因为,,,
所以数列,,2的最佳值为;
对于数列,2,,
因为,,,
所以数列,2,的最佳值为1;
对于数列2,,,
因为,,,
所以数列2,,的最佳值为1;
对于数列2,,,
因为,,,
所以数列2,,的最佳值为;
对于数列,,2,
因为,,,
所以数列,,2的最佳值为;
对于数列,2,,
因为,,,
所以数列,2, 4的最佳值为
∴数列的最佳值的最小值为,数列可以为:,2,或2,,.
故答案为,,2,或2,,.
(3)当时,则或,不合题意;
当,则或7;
当时,数列为,7,2,因为,,,
所以数列,7,2的最佳值为0,不符合题意;
当,则或10.
∴或4或10.
【点睛】此题考查数字的变化规律,理解新定义运算的方法是解决问题的关键.
48.(1);6;7
(2)7或
(3)
(4)2或3
(5);7
【难度】0.4
【分析】(1)由最大的负整数与绝对值的含义可得,的值,再求解两点之间的距离即可;
(2)由,再分三种情况讨论即可;
(3)由,再分三种情况讨论即可;
(4)由,可得或;再结合(2)可得结论;
(5)先求解,再结合绝对值的含义可得答案.
【详解】(1)解:∵点A表示的数a为最大的负整数,点B表示的数b在原点右侧,且绝对值为6,
∴,,
∴数轴上A,B两点之间的距离为;
(2)∵,
∴,
当时,,
∴,
当时,
∴,
方程无解;
当时,
∴,
解得:;
(3)∵,
当时,原式,
当时,
∴原式,
当时取得最小值;
当时,
∴原式;
综上:的最小值为;
(4)∵,
∴,
∴或;
当时,
结合(2)得:此时,
∴,
解得:,
当,结合(2)得:此时,
∴,
解得:,
综上:或;
(5)∵正实数c满足,
∴,
∴,
∵,
∴结合绝对值的含义可得当时,取得最小值,
最小值为:.
【点睛】本题考查的是数轴上两点之间的距离,绝对值的应用,一元一次方程的应用,利用平方根的含义解方程,二次根式的加减运算,掌握绝对值的几何意义是解本题的关键.
49.(1),12,
(2)①当t的值为2或8时,点P、Q两点到点A的距离相等;②
【难度】0.85
【分析】本题考查了一元一次方程的应用以及数轴,
(1)先利用非负性求出,即可表示出两点A、B对应的数,从而表示出点P表示的数;
(2)①先表示出,,再建立等式求解;②先表示出点Q表示的数,点M表示的数,再表示出,通过计算出,再根据与t无关即可求解.
【详解】(1)解:,
,,
,,
点A表示的数为,点B表示的数为12,点P表示的数,
故答案为:,12,.
(2)解:①,
由点P、Q两点到点A的距离相等,得,
,
解得:或8;
②点Q表示的数,点M表示的数.
则,,
,
∵式子的值不随时间t的变化而变化,
∴,
∴.
50.(1),,
(2)
(3)的取值是或3
【难度】0.65
【分析】(1)根据点在数轴上的位置,判断出式子的符号即可;
(2)先判断出式子的符号,再化简绝对值即可;
(3)分,,,,,和,,进行讨论求解即可.
【详解】(1)解:由图可知:,,
∴,,;
故答案为:,,;
(2)解:∵,,,
∴原式
;
(3)
,
①当,时,则
;
②当,时,则
;
③当,时,则
;
④当,时,则
.
综上所述:的取值是或3.
【点睛】本题考查利用数轴判断式子的符号,化简绝对值,整式的加减运算,利用数形结合和分类讨论的思想进行求解,是解题的关键.
51.(1)单位长度
(2)秒或秒
(3)正确,这个时间是秒,定值是个单位长度
【难度】0.4
【分析】(1)根据非负数的性质求出,,求差即可求解;
(2)根据时间=路程和÷速度和,设行驶秒钟两列火车行驶到车头和相距单位长度,列方程即可求解;
(3)由于,只需要是定值,从快车上乘客与慢车相遇到完全离开之间都满足是定值,依此分析即可求解.
【详解】(1)解:∵与互为相反数,
∴,
∴,,
解得:,,
∴此时刻快车头与慢车头之间相距(单位长度);
答:此时快车头与慢车头之间相距单位长度;
(2)设行驶秒钟两列火车行驶到车头和相距个单位长度,
两车相遇前可列方程为
,
解得,;
两车相遇后可列方程为
,
解得,;
答:再行驶秒或秒,两列火车行驶到车头和相距个单位长度;
(3)正确.理由如下:
∵六年级学生乘客在快车上,
∴,
当在之间时,是定值,即路程为,
∴行驶时间:(秒),
此时(单位长度),
∴这个时间是秒,定值是个单位长度.
【点睛】本题考查一元一次方程的应用,数轴、绝对值和偶次方的非负性,数轴上两点之间的距离,熟练掌握行程问题的等量关系:时间=路程÷速度,本题难度较大.方程思想和数形结合思想的应用是解题的关键.
52.(1)
(2)的值为5或
(3)①6,②420或440或460或
【难度】0.4
【分析】此题考查了绝对值的应用,解题的关键是理解“双倍关系值”的定义,熟练掌握绝对值的性质.
(1)根据“双倍关系值”的定义,求解即可;
(2)根据“双倍关系值”的定义,列方程,求解即可;
(3)①根据题意列出方程,再分为四种情况,分别讨论,根据绝对值的性质,把绝对值方程转化为常规方程进行解答便可;②分10种情况计算即可.
【详解】(1)解:由题意得:
,
故答案为:;
(2)解:由题意得:,即,
,
或,
解得:或,
的值为5或;
(3)解:①和关于1的“双倍关系值”为2,
,
分四种情况:
当时,,则;
当时,,则,即;
当时,,则;即;
当时,,则;
综上,的最大值为6,
故答案为:6;
②分10种情况:
1、当时,,解得,
由可得,,
……,
可得,
;
2、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
3、当时,,解得:或,
时,由,可得,此种情形不存在;
时,由,解得:或,
时,由,可得,此种情形不存在;
时,由,解得:或,
,
同理得:,
;
4、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
5、当,由,解得:或,
时,与矛盾,此种情形不存在;
,则,解得:或,
时,与矛盾,此种情形不存在;
,
同理:,,……,;
,即;
,即;
;
6、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
7、当,由,可得,解得:或,
时,与矛盾,此种情形不存在;
,
当时,由,可得,解得:或,
,与矛盾,此种情形不存在;
,
同理:,,……,;
;
8、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
9、当时,,解得,
由可得,,
……,
可得,
;
10、当时,,与矛盾,此种情形不存在;
综上所述:的值为420或440或460或,
故答案为:420或440或460或.
53.(1)2
(2)存在,或7
(3)或
【难度】0.85
【分析】本题主要考查非负性、两点之间的距离和一元一次方程的应用,
(1)根据相反数的意义,平方的非负性和绝对值的非负性求得a和b,利用两点之间距离即可求得;
(2)根据题意将距离之和表示为,利用数轴上两点之间距离去绝对值即可求得答案;
(3)先将第t分钟点A、B和P表示出,进一步求得和的距离,根据题意列出等式,解绝对值方程即可;
【详解】(1)解:∵,
∴,.
设P点对应的数为x,根据数轴得:,解得:,
则P对应的数为:2.
(2)根据题意得:,
由于点和点B之间距离为8,则点P只能位于A和B两侧,
当时,化简得:,即;
当时,化简得:,即;
故点P为或7时到点A和点B的距离之和为10.
(3)设第t分钟时,点P到点A、点B的距离相等.
∵A:,B:,P:,
∴.
.
∵,
∴.
则当,解得:;
当,解得:;
∴在分钟或分钟时距离相等.
54.(1)4;3
(2)
(3)
【难度】0.65
【分析】(1)根据数轴上、两点之间的距离计算便可;
(2)根据数轴上、两点之间的距离解答便可;当在表示数与2的两点及两点之间时,利用绝对值性质化简即可;
(3)利用分类讨论的数学思想解答本题.
【详解】(1)数轴上表示1和5两点之间的距离是,数轴上表示2和的两点之间的距离是,
故答案为:4;3
(2)数轴上表示x和两点之间的距离为.
∵x表示一个有理数,且,
∴,
故答案为:;
(3)由数轴可知,当时,取得最小值,
最小值是:,
此时,可取的整数值是:.
即的最小值是8,此时可取的整数值是:.
故答案为:.
【点睛】本题考查数轴上两点间的距离、绝对值,解题的关键是利用分类讨论的思想去绝对值符号.
一、数字类规律探索
1.如图,图1所示的数字规律表,已知图2是从图1中按未显示部分截取下来的一部分,则△处的数字不可能是( )
A.75 B.50 C.26 D.9
2.记的所有正因数为,,…,,则( )
A. B. C. D.
3.在数学上,常用符号来简洁地表示多个数求和,例如表示把代数式取为1,2,3,……,99,100时的代数式的值分别求和,即结果为,则的结果为( )
A. B. C. D.
4.将正整数按下表规律排列:表中数2在第二行、第一列,与有序数对对应,数5与对应;数14与对应;根据这一规律,数2023对应的有序数对为( )
第一列 二列 三列 四列 五列 …
第一行 1 4 5 16 17
第二行 2 3 6 15 …
第三行 9 8 7 14
第四行 10 11 12 13
第五行
…
A. B. C. D.
5.我们规定:表示不超过x的最大整数.如:,.现已知对所有正整数n成立,则的值为 .
6.现有一列数:,,,,,,(为正整数),规定,,,,,则的值为 .
7.已知有理数a≠1,我们把称为a的差倒数,如:2的差倒数是=﹣1,﹣1的差倒数是.如果a1=﹣2,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……依此类推,那么a1+a2+…+a100的值是 .
8.若a是不为2的有理数,我们把称为a的“牛顿数”.如3的“牛顿数”是,的“牛顿数”是,已知,是的“牛顿数”,是的“牛顿数”,是的“牛顿数”,…,依此类推,则 .
9.在明代的《算法统宗》一书中将用格子的方法计算两个数相乘称作“铺地毯”,如图1,计算,将乘数82记入上行,乘数34记入右行,然后用乘数82的每位数字乘以乘数34的每位数字,将结果记入相应的格子中,最后按斜行加起来,既得2788.如图2,用“铺地毯”的方法表示两个两位数相乘,则= ,= .
10.如图,在的方格中,每个小方格的边长为1且标记数字,在方格中画阴影正方形.现规定被阴影正方形全部覆盖的小方格,其数值之和记为m,部分覆盖的小方格,其数值之和的一半记为n.以图1中阴影正方形为例,.若在图2中画一个面积为5的阴影正方形(顶点均在格点上),且,则m的值为 .
11.在探究“幻方”、“幻圆”的活动课上,学生们感悟到我国传统数学文化的魅力.如图,某小组同学尝试将数字,,,,,,0,1,2,3,4,5这12个数填入“六角幻星”图中,使6条边上四个数之和都相等.部分数字已填入圆圈中,则a的值为
12.如图,第(1)个多边形由正三角形“扩展”而来,边数记为,第(2)个多边形由正方形“扩展”而来,边数记为,…,依此类推,由正边形“扩展”而来的多边形的边数记为
(1) ;
(2) .
二、图形类归路探索
13.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10个图形需要黑色棋子的个数是( )
A.120个 B.122个 C.130个 D.132个
14.电子跳蚤游戏盘(如图)为,,,,如果电子跳蚤开始时在BC边的点,,第一步跳蚤从跳到AC边上点,且;第二步跳蚤从跳到AB边上点,且;第三步跳蚤从跳回到BC边上点,且;……跳蚤按上述规则跳下去,第n次落点为.则与之间的距离为( )
A.0 B.1 C.4 D.5
15.用边长相等的正方形和等边三角形卡片按如图所示的方式和规律拼出图形.拼第1个图形所用两种卡片的总数为7枚,拼第2个图形所用两种卡片的总数为12枚若按照这样的规律拼出的第个图形中,所用正方形卡片比等边三角形卡片多10枚,则拼第个图形所用两种卡片的总数为( )
A.57枚 B.52枚 C.50枚 D.47枚
16.用若干根长为1的火柴恰好可以拼成如图1所示的47个边长为1的正方形,若将这些火柴按如图2所示的方式拼,则可以拼出 个边长为1的正方形.
17.用正方形按如图所示的规律拼图案,其中第①个图案中有个正方形,第②个图案中有个正方形,第③个图案中有个正方形,第④个图案中有个正方形,此规律排列下去,则第⑨个图案中正方形的个数为 .
三、整式加减的应用
18.如图,6张全等的小长方形纸片放置于矩形中,设小长方形的长为,宽为,若要求出两块黑色阴影部分的周长差,则只要测出下面哪个数据( )
(小蜜蜂提醒:小长方形有部分重叠)
A. B. C. D.
19.如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为,下列说法中正确的有( )
①小长方形的较长边为;
②阴影的较短边和阴影的较短边之和为;
③若为定值,则阴影A和阴影B的周长和为定值;
④当时,阴影A和阴影B的面积和为定值.
A.①② B.①③ C.①③④ D.①②③
20.如图,在一个正方形的内部放置大小不同的两个小正方形,其中较大的正方形的面积为15,重叠部分的面积为1,空白部分的面积为,则较小的正方形面积为( )
A.4 B. C.9 D.
21.已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形,小明把这2个小长方形按如图所示放置在大长方形中,小明经过推事得知,要求出图中阴影部分的周长之和,只需知道a、b、m、n中的一个量即可,则要知道的那个量是( )
A.a B.b C.m D.n
22.如图1,周长为16的长方形纸片剪成①,②,③,④号正方形和⑤号长方形,并将它们按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为 .
23.如图,5张完全一样的长方形卡片放入一张面积为17的正方形卡片中(卡片不重叠,无缝隙),则未被长方形卡片覆盖的A区域与B区域的周长和为 .
24.现有三种边长分别为3,2,1的正方形卡片(如图1),分别记为Ⅰ,Ⅱ,Ⅲ.还有一个长为a,宽为b的长方形.将Ⅰ,Ⅱ,Ⅲ三张卡片按图2的方式,放置在长方形中,则右上角阴影部分与左下角阴影部分周长的差为 .
四、数轴上两点之间的距离和动点问题
25.一把刻度尺的部分在数轴上的位置摆放如图所示,若刻度尺上的刻度“”和“”分别对应数轴上的和,现将该刻度尺沿数轴向右平移个单位,则刻度尺上对应数轴上的数为 .
26.如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示 2的点重合,再将圆沿着数轴向右滚动,则数轴上表示2023的点与圆周上表示哪个数字的点重合?( )
A.0 B.1 C.2 D.3
27.在数学上,不但可以表示5与之差的绝对值,也可以理解为5与两数在数轴上所对应的两点之间的距离,则使得这样的整数一共有( )个
A.7 B.6 C.5 D.4
28.如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上0,1,2,3,先让圆周上表示数字0的点与数轴上表示的点重合,再将圆沿着数轴向右滚动,则圆周上表示数字 的点与数轴上表示2023的点重合.
29.长方形在数轴上的位置如图所示,点B、C对应的数分别为和,.若长方形绕着点C顺时针方向在数轴上翻转,翻转1次后,点D所对应的数为2;绕点D翻转第2次;继续翻转,则翻转2023次后,落在数轴上的两点所对应的数中较大的是 .
30.等边在数轴上的位置如图所示,点A、C对应的数分别为0和,若绕顶点按顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转次后,点B对应的数是 .
31.如图,数轴上的点A表示数,点B表示数3,图形I和图形II都有3个边长为1个单位的正方形组成且底边均落在数轴上,开始时,图形的顶点P与顶点A重合,图形II的顶点Q与点B重合,现图形I以每秒3个单位长度的速度向数轴正方向运动,同时图形II以每秒个单位长度的速度向数轴正方向运动.
(1)点A与点B的距离是__________个单位长度.
(2)经过多少时间后,图形I与图形II并行(点P与点Q重合),并求此时点P表示的数.
(3)在运动过程中,当两个图形重叠部分的面积与未重叠部分的面积之比为时,则点P表示的数是__________(直接写出答案).
32.已知:A,B在数轴上,且满足.点B向右平移个单位得到点C,点C向右平移个单位得到点D,点A,B,C,D对应的数分别为a,b,c,d,.
(1) , .
(2)用含n的代数式表示c和d, , .
(3)定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就称点C是的美好点.有理数a,b,c,d,四个数的积为负数,点C,D中存在的美好点,求n的值.
33.如图,动点A,B同时从表示数1的位置出发沿数轴做匀速运动,已知动点A,B运动速度之比是(速度单位:1个单位长度/秒).若经过4秒,点A运动到点M,点M表示的数为,点B运动到点N,且点N在原点的右侧.
(1)点N表示的数为 ;
(2)若动点A,B分别由M,N两点位置同时开始继续按原速运动,且在数轴上的运动方向不限.
①若A,B两点同向运动,当点A运动到与表示数1的位置相距13个单位长度时,求此时点B表示的数.
②若A,B两点在这段运动过程中有段时间内,点B所表示的数与点A所表示的数的和与差均为非负数,则相应这段时间持续了 秒(直接写出答案).
34.如图,数轴上有A,B两点,A,B之间距离为15,原点O在A,B之间,O到A的距离是O到B的距离的两倍.
(1)点A表示的数为______,点B表示的数为______.
(2)点A、点B和点P(点P初始位置在原点O)同时向左运动,它们的速度分别为1,2,2个单位长度每秒,则经过多少秒,点P到点A与点B的距离相等?
(3)点B沿着数轴移动,每次只允许移动1个单位长度,经过6次移动后,点B与原点O相距1个单位长度.满足条件的点B的移动方法共有多少种?
(4)点A和点B同时沿着数轴移动,两点每次均只允许移动1个单位长度.请判点A和点B经过相同次数的移动后,能否同时到达原点O?如果能,请给出点A和点B各自的移动方法:如果不能,请说明理由.
35.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长(单位长度),慢车长(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点为原点,取向右方向为正方向画数轴,此时快车头在数轴上表示的数是,慢车头在数轴上表示的数是.若快车以4个单位长度/秒的速度向右匀速继续行驶,同时慢车以2个单位长度/秒的速度向左匀速继续行驶,且与互为相反数.
温馨提示:忽略两辆火车的车身及双铁轨的宽度.
(1)求此时刻快车头与慢车头之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头相距6个单位长度?
(3)此时在快车上有一位爱动脑筋的七年级学生乘客,他发现行驶中有一段时间秒钟,他的位置到两列火车头、的距离和加上到两列火车尾、的距离和是一个不变的值(即为定值).你认为学生发现的这一结论是否正确?若正确;求出这个时间的值和这个不变值;若不正确,请说明理由.
36.如图,在数轴上有A,B两点,分别表示的数为a,b,且.点P从A点出发以每秒19个单位长度的速度沿数轴向右匀速运动,当它到达B点后立即以相同的速度返回往A点运动,并持续在A,B两点间往返运动.在点P出发的同时,点Q从B点出发以每秒3个单位长度向左匀速运动,当点Q到达A点时,点P,Q停止运动.
(1)________(填空),并求运动了多长时间后,点P,Q第一次相遇,以及相遇点所表示的数;
(2)点C在数轴上对应的数为81,在数轴上是否存在点M,使,若存在,求出点M对应的数,若不存在,说明理由;
(3)求当点P,Q停止运动时,点P所在的位置表示的数;在整个过程中,点P和点Q一共相遇了多少次?
37.已知数轴上A,B两点对应的数字分别是,4,如果把点A往左移动4个单位长度到达点C.动点P以每秒a个单位长度的速度从点C出发往数轴正方向运动,同时动点Q以每秒b个单位长度的速度从点A出发往数轴正方向运动,且.
(1)点A和点B的距离是______,点C对应的数字是______.
(2)若经过3秒后,点P与点Q重合,求的值.
(3)在运动过程中,
①当点P与点Q的距离是2个单位长度且点P位于点Q的左侧时,则所经过的时间为______.(用含a,b的代数式表示)
②若,,当点P与点Q的距离与点A与点B距离之比为时,求此时点P表示的数.
38.【背景知识】数轴是初中数学学习的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律,例如:若数轴上点A,B分别对应数a,b.则A,B两点之间的距离为.
【问题情境】如图,数轴上点A,B分别对应数a,b.其中.
【综合运用】
(1)当时,线段的长度是__________;
(2)若该数轴上另有一点N对应着数n.
①在(1)的条件下,若点N在点A,B之间,且满足,则数n是__________;
②当,且时,探究a与n之间的数量关系.
39.数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小白在草稿纸上画了一条数轴进行操作探究:
操作一:
(1)折叠纸面,若使1表示的点与-1表示的点重合,则-2表示的点与______表示的点重合;
操作二:
(2)折叠纸面,若使1表示的点与-3表示的点重合,回答以下问题:
①3表示的点与______表示的点重合;
②若数轴上、两点之间距离为7(在的左侧),且、两点经折叠后重合,则、两点表示的数分别是______;
操作三:
(3)在数轴上剪下8个单位长度(从-2到6)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图).若这三条线段的长度之比为,则折痕处对应的点所表示的数可能是______.
40.如图1.在数轴上点M表示的数为m,点N表示的数为n,点M到点N的距离记为.我们规定:的大小用位于右边的点表示的数减去左边的点表示的数表示,即.请用上面的知识解答下面的问题:如图2:在数轴上点A表示数a,点B表示数b,点C表示数c,b是最大的负整数.且a,c满足与互为相反数.
(1) , , ;
(2)若将数轴折叠,使得A点与C点重合,则点B与表示数 的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟后.
①请问:的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
②探究:若点A,C向右运动,点B向左运动,速度保持不变,的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.
41.如图,将两个形状完全相同的长方形,放置在数轴上,它们的长为2,宽为1,C与表示的点重合,F与表示3的点重合.长方形以每秒1个单位长度的速度沿数轴向右运动,同时长方形以每秒2个单位长度的速度沿数轴向左运动.设运动时间为t.
(1)当时,点C表示的数为______,点F表示的数为______.
(2)当点C和点F重合时,求t的值.
(3)在运动过程中,两个长方形会出现重叠部分
①请求出有重叠部分时持续的时间.
②当重叠部分周长是长方形周长的一半时,请直接写出此时点C所表示的数为______.
42.实践与探究
【实践】
求出下列每对数在数轴上对应点之间的距离:
(1)与;
(2)与;
(3)与.
【探案】
结论:数轴上两点之间的距离等于这两个点对应数的差的绝对值.
(1)数轴上表示数与1的两点之间的距离可用符号语言记作______.
(2)的含义是数轴上表示数与______的两点之间的距离;
(3)若,则______.
【应用】
如图,长方形和各有一条边在数轴上,长方形的一条边长为2,长方形的一条边长为1,四个点对应的数分别为.用和分别表示两个长方形的面积,求这两个长方形的面积(用含的代数式表示)并比较它们的大小.
43.如图,点为数轴的原点,点表示的数为,边长为的正方形在数轴上,此时点在点左边,且点与点的距离为.
(1)写出数轴上点表示的数为______.
(2)若正方形以每秒个单位长度的速度沿数轴向右运动,同时点以每秒个单位长度从原点出发沿数轴向右运动.
①当,两点相遇时,请求出此时点在数轴上表示的数.
②在整个运动过程中,当点遇到点时,立即以原速度沿数轴向左运动.若点与点的距离等于点到点的距离,此时在数轴上表示的数为______.(直接写出答案即可)
五、实数与数轴
44.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A、B两点表示的数分别为___________,____________;
(2)请你参照上面的方法:
①把图3中的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长___________.(注:小正方形边长都为1,拼接不重叠也无空隙)
②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及.(图中标出必要线段的长)
六、绝对值的意义
45.已知.
(1)用的代数式表示为______;用的代数式表示为______.
(2)求代数式的值.
(3)均为整数,且,求满足条件的的值.
46.已知点A在数轴上对应的数为,点在数轴上对应的数为,,且,A、之间的距离为或,请回答问题:
(1)请直接写出 , , ;
(2)设点在数轴上对应的数为,且,求的值;
(3)如图,点,,是数轴上的三点,点表示的数为4,点表示的数为,动点表示的数是.
①若,求的值;
②求的最小值,并写出此时整数的值.
47.东东在研究数学问题时遇到一个定义:将三个已经排好顺序数,称为数列,计算,,,将这三个数的最小值称为数列的最佳值.例如,对于数列2,,3,因为,,,所以数列2,,3的最佳值为.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列,2,3的最佳值为;数列3,,2的最佳值为1;….经过研究,东东发现,对于“2,,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为.根据以上材料,回答下列问题:
(1)数列,,1的最佳值为
(2)将“,,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,,这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
48.数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.通过研究数轴,我们发现了许多重要的规律,比如:数轴上点A和点B表示的数为a,b,则A,B两点之间的距离.若点A表示的数a为最大的负整数,点B表示的数b在原点右侧,且绝对值为6,则
(1)点A表示的数a为______,点B表示的数b为______,数轴上A,B两点之间的距离为______;
(2)满足的实数x的值为______;
(3)的最小值为______;
(4)满足的实数x的值为______;
(5)若正实数c满足,则当x的值为______时,取到最小值______.
49.如图,已知数轴上两点A、B对应的数分别为a、b,且.动点P从点B出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒().
(1)写出数轴上点A表示的数为 ,点B表示的数为 ,点P表示的数为______(用含t的式子表示);
(2)动点Q从点A出发,以每秒3个单位长度的速度向左匀速运动,动点M从点B出发,以每秒1个单位长度的速度向右匀速运动,且点P、Q、M同时出发.
①当t为何值时,点P、Q两点到点A的距离相等?
②式子的值不随时间t的变化而变化,求m的值.
50.已知有理数理数、、在数轴上的位置如图:
(1)用“”或“”填空:
__________,__________,__________0.
(2)化简:.
(3)若数轴上存在两点、,,则的值是多少?
51.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长(单位长度),慢车长(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头在数轴上表示的数是,慢车头在数轴上表示的数是.若快车以个单位长度/秒的速度向右匀速继续行驶,同时慢车以个单位长度/秒的速度向左匀速继续行驶,且与互为相反数.
(1)求此时刻快车头与慢车头之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头和相距个单位长度.
(3)此时在快车上有一位爱动脑筋的六年级学生乘客,他发现行驶中有一段时间秒钟,他的位置到两列火车头,的距离和加上到两列火车尾,的距离和是一个不变的值(即为定值).你认为学生发现的这一结论是否正确?若正确,求出这个时间及定值;若不正确,请说明理由.
52.阅读信息:
信息一:的几何意义是x与y两数在数轴上所对应的两点之间的距离.例如的几何意义是3与1两数在数轴上所对应的两点之间的距离.
信息二:对于有理数a,b,n,d,若,则称a和b关于n的“双倍关系值”为d.例如,,则6和3关于1的“双倍关系值”为5.
根据以上信息回答下列问题:
(1)和5关于2的“双倍关系值”为______.
(2)若a和3关于1的“双倍关系值”为4,求a的值;
(3)若和关于1的“双倍关系值”为2,和关于2的“双倍关系值”为2,和关于3的“双倍关系值”为2,…,和关于21的“双倍关系值”为2.
①的最大值为______;
②的值为______(用含的式子表示).
53.数轴上有A、B两点,分别对应的数为a,b,已知与互为相反数.点为数轴上一动点,对应的数为x.
(1)若点P到点A和点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A和点B的距离之和为10?若存在,请求出x的值;若不存在,说明理由;
(3)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,点B以每分钟20个单位长度的速度向左运动,问几分钟时点P到点A、点B的距离相等?
54.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为.在数轴上A、B两点之间的距离.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是______,数轴上表示2和的两点之间的距离为______.
(2)数轴上表示x和两点之间的距离为______,若x表示一个有理数,且,则______.
(3)利用数轴求出的最小值为______,并写出此时x可取哪些整数值______.
参考答案:
题号 1 2 3 4 13 14 15 18 19 20
答案 B A D B A A B B C C
题号 21 26 27
答案 D B A
1.B
【难度】0.65
【分析】本题考查数字规律探究.
根据数字规律表可知,偶数行为负数,奇数行为正数;第二行的数是第一行数正序对应数的倍,第三行的数是第一行数反序后对应数的倍,第四行的数是第一行数反序后对应数的倍,第五行的数是第一行对应数的倍,,则第一行从第一行到第四行的排序方式是正序、正序、反序、反序的方式循环;第行就是倍,偶数行时为,奇数行时为;按此规律列出所以可能情况即可判断.
【详解】解:根据题意,当在第6行时,△在第7行,数字为第一行反序后对应数的倍,即为;
当在第8行时, △在第9行,数字为第一行数正序对应数的倍,即为;
当在第12行时, △在第13行,数字为第一行数正序对应数的倍,即为;
当在第24行时, △在第25行,数字为第一行数正序对应数的倍,即为;
综上所述,可能出现的数字为:,
∴不可能出现的数字是50,
故答案为:B.
2.A
【难度】0.65
【分析】本题考查了数字类变化规律,根据题意计算归纳得出若的所有正约数为,,…,,则,再结合,得出,即可得出答案,得出规律是解此题的关键.
【详解】解:对于的个正约数1,,,有,
对于的个正约数,,,有,
对于的个正约数,,,,,有,
对于的个正约数,,,有,
对于的个正约数,,,,,,,,,有,
…,
若的所有正约数为,,…,,则,
,
,
当时,,
故选:A.
3.D
【难度】0.65
【分析】本题主要考查了有理数混合运算,解题的关键是根据题意得出,求出即可得出答案.
【详解】解:
,
设,
则,
∴,
解得:,
∴,
即.
故选:D.
4.B
【难度】0.85
【分析】此题主要考查了数字的规律知识,得出第一列的奇数行的数的规律与第一行的偶数列的数的规律是解决问题的关键.
根据已知数据可得出第一列的奇数行的数的规律是第几行就是那个数平方,同理可得出第一行的偶数列的数的规律,从而得出2023所在的位置.
【详解】解:由已知可得:根据第一列的奇数行的数的规律是第几行就是那个数平方,第一行的偶数列的数的规律,与奇数行规律相同;
∵,在第45行,
∵向右依次减小,
∴2023所在的位置是第45行,第3列,
∴其有序数对.
故选:B.
5.301
【难度】0.4
【分析】本题考查了无理数的估算,掌握算术平方根的意义及新定义的意义是解题的关键;根据的意义,对每个无理数进行估算即可.
【详解】解:当时,;当时,;当时,;当时,;当时,;当时,;当时,;
∴
.
故答案为:301.
6.
【难度】0.65
【分析】本题考查数字变化的规律,解题的关键是能根据题意依次求出,,,,,及熟知(为正整数).据此解答即可.
【详解】解:由题意得:
,
,
,
∴,
∴(为正整数),
∴
.
故答案为:.
7.
【难度】0.4
【分析】根据题意,先求出这列数的前几项,从而得出这个数列以-2,,依次循环,且-2++=-,再求出这100个数中有多少个循环组,从而得出答案.
【详解】解:∵a1=-2,
,
,
,
……
∴这个数列以-2,,依次循环,且-2++=-,
∵100÷3=33…1,
∴a1+a2+…+a100=33×(-)-2=-.
故答案为:-.
【点睛】本题是对数字变化规律的考查,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.
8.
【难度】0.65
【分析】本题考查了数字的规律变化,通过观察数字,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键.根据题意易得,, ,,…,由此可得该组数是4个一循环,进而问题可求解.
【详解】解∶∵,是的“牛顿数”,
∴,
∵是的“牛顿数”,
∴,
∵是的“牛顿数”,
∴,
∵是的“牛顿数”,
∴,
…,
∴,,,四个一循环,
∵,
∴.
故答案为:.
9. 3 6
【难度】0.65
【分析】本题考查了古籍数学的认识和应用,设的十位数是m,个位数是n,根据“铺地毯”法则,建立等式计算即可.
【详解】设的十位数是m,个位数是n,
根据题意,如图,
∴,
∴,
∴,
∴,
故答案为:3, 6.
10.12
【难度】0.65
【分析】本题考查的是图形的变化规律,关键是通过图1中面积为10的阴影正方形,分析出图2中面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;然后列式求解即可.
图1中阴影正方形的面积为10,被全部覆盖的小方格有4个,被部分覆盖的小方格有10个;则面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为、、、、、、、;因,将式子进行化简计算即可.
【详解】解:如图所示,
面积为5的阴影正方形,被全部覆盖的小方格有1个,被部分覆盖的小方格有8个;
被全部覆盖的小方格数值即为m,被部分覆盖的小方格,数值分别为;
因为,即,
,
解得:.
故答案为:12.
11.
【难度】0.65
【分析】本题考查了一元一次方程的应用.根据“使6条边上四个数之和都相等”列方程求解.
【详解】解:设右下边为x,由满足6条边上四个数之和都相等,他们的和为,如图所示:
观察图形还有,,,2,3,5六个数字,
观察“六角幻星”图可知与相差6,只有,5或2,满足,
则或,
解得:或(不合题意,舍去),
故答案为:.
12.
【难度】0.65
【分析】(1)结合图形观察数字,发现:,,进一步得到;
(2)在计算的时候,根据,…进行简便计算.
【详解】,
,
,
,
,
∴,
,
故答案为:;.
【点睛】此题考查了图形的变化规律题,找到规律,利用分数的加减法进行简便计算是解题的关键.
13.A
【难度】0.85
【分析】此题考查图形的变化规律.由图可知:则第n个图形需要黑色棋子的个数是.由此代入求得答案即可.
【详解】解:∵第1个图形需要黑色棋子的个数是,
第2个图形需要黑色棋子的个数是,
第3个图形需要黑色棋子的个数是,
…,
∴第n个图形需要黑色棋子的个数是;
则第10个图形需要黑色棋子的个数是.
故选:A.
14.A
【难度】0.65
【分析】根据题意分别求出电子跳蚤每次跳后的位置,从而得到点P6与点P4重合,然后用2014除以6,根据余数是4可得P2014与P4重合,从而得解.
【详解】解:∵BC=10,BP0=4,
∴CP0=6,
第一步:CP1=CP0=6,
∵AC=9,
∴AP1=9-6=3,
第二步:AP2=AP1=3,
∵AB=8,
∴BP2=5,
第三步:BP3=BP2=5,
依此类推,第四步,CP4=CP3=5,
第五步,AP5=AP4=4,
第六步,BP6=BP5=4,
此时P6与P0重合,即经过6次跳,电子跳蚤回到起跳点,
∵2014÷6=335余4,
∴P2014是第336循环组的第4步,与P4重合,
此时P4与P2014之间的距离是0.
故选:A.
【点睛】本题是对图形变化规律的考查,读懂题目信息求出各步跳动后的位置,并且得到经过6次跳,电子跳蚤回到起跳点是解题的关键.
15.B
【难度】0.85
【分析】总结规律第个图形中所用正方形卡片比等边三角形卡片多几枚,当时,求出所用正方形卡片及等边三角形卡片的数量,栽求和即可得到答案.
【详解】解:第1个图形中所用正方形卡片比等边三角形卡片多(枚),
第2个图形中所用正方形卡片比等边三角形卡片多(枚),
第3个图形中所用正方形卡片比等边三角形卡片多(枚),
第个图形中所用正方形卡片比等边三角形卡片多(枚),
当时,所用正方形卡片为:(枚),所用等边三角形卡片为:,
所用两种卡片的总数为:(枚),
故选:B.
【点睛】本题考查了与有理数有关的规律探究,解题的关键是总结规律第个图形中所用正方形卡片比等边三角形卡片多几枚.
16.56
【难度】0.85
【分析】本题主要考查了图形规律探索,一元一次方程的应用,解题的关键是根据图形得出规律,先求出拼成图1所示的47个边长为1的正方形,需要的火柴棒的根数为142根,设这些火柴按如图2所示的方式拼,可以拼成的正方形个数为x个,根据图形规律列出方程,解方程即可.
【详解】解:拼成图1所示的47个边长为1的正方形,则需要的火柴棒的根数为:
(根),
设这些火柴按如图2所示的方式拼,可以拼成的正方形个数为x个,根据题意得:
,
解得:,
即可以拼出56个边长为1的正方形.
故答案为:56.
17.
【难度】0.85
【分析】根据图形变化的规律得出第个图形中有个正方形即可解答
【详解】解:由题知,第①个图案中有个正方形,第②个图案中有个正方形,第③个图案中有个正方形,第④个图案中有个正方形,…,第n个图案中有个正方形,
∴第⑨个图案中正方形的个数为,
故答案为:.
【点睛】本题考查了图形的变化规律,根据图形的变化得出第个图形中有个正方形是解题的关键.
18.B
【难度】0.65
【分析】本题考查整式加减的应用,准确识图,利用平移思想分析得出两块阴影部分的周长之差即为长方形和长方形的周长之差是解题关键.延长交于点K,根据图形得出,,,,根据题意得出,两块阴影部分的周长差为:,然后去括号,合并同类项得出结果,作出判断即可.
【详解】解:延长交于点K,如图所示:
由题意可得:,,,,
结合平移思想可得两块阴影部分的周长之差即为长方形和长方形的周长之差,
两块阴影部分的周长差为:
,
若要求出两块黑色阴影部分的周长差,则只要测出数据b,
故选:B.
19.C
【难度】0.65
【分析】先根据图形即题目给出的数据得出阴影A、阴影B和5个小长方形的较长边和较短边,分别按照①②③④的要求进行计算即可.
【详解】解:由题可知,阴影A的较长边为,较短边为;
阴影B的较长边为12,较短边为;
小长方形的较长边为,较短边为4,
则①小长方形的较长边为,故①正确;
②阴影A的较短边和阴影B的较短边之和为,故②错误;
③阴影A和阴影B的周长和为,若x为定值,则阴影A和阴影B的周长和为定值,故③正确;
④阴影A和阴影B的面积和为,当时,阴影A和阴影B的面积和为240,是一个定值,故④正确.
综上可知,正确的为①③④.
故答案选C.
【点睛】本题考查了整式加减的运用,准确计算是解题关键.
20.C
【难度】0.85
【分析】本题主要考查了二次根式的应用,观察图形得到各个正方形边长之间的关系是解题的关键.根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
【详解】解:∵观察可知,两个空白部分的长相等,宽也相等,
∴重叠部分也为正方形,
∵空白部分的面积为,
∴一个空白长方形面积为,
∵大正方形面积为15,重叠部分面积为1,
∴大正方形边长为,重叠部分边长1,
∴空白部分的长为,
设空白部分宽为x,可得:,解得:,
∴小正方形的边长=空白部分的宽+重叠部分边长,
∴小正方形面积,
故选:C.
21.D
【难度】0.94
【分析】先用含a、b、m、n的代数式表示出阴影矩形的长宽,再求阴影矩形的周长和即可.
【详解】解:如图,由图和已知条件可知:AB=a,EF=b,AC=n﹣b,GE=n﹣a.
阴影部分的周长为:2(AB+AC)+2(GE+EF)
=2(a+n﹣b)+2(n﹣a+b)
=2a+2n﹣2b+2n﹣2a+2b
=4n.
∴求图中阴影部分的周长之和,只需知道n一个量即可.
故选:D.
【点睛】本题主要考查了整式的加减,能用含a、b、m、n的代数式表示出阴影矩形的长宽是解决本题的关键.
22.
【难度】0.65
【分析】本题考查整式加减法与几何图形的应用,巧妙设未知数,列出代数式表示各个图形的边长,利用整体思想求值是解答的关键.
在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,根据图1的周长求得,再根据图2的周长求得,进而可由没有覆盖的阴影部分的周长为求解即可.
【详解】解:在图1中,设①号正方形的边长为x,②号正方形的边长为y,则③号正方形的边长为,④号正方形的边长为,
由图1中长方形的周长为16得,
解得:,
如图2,
由图2中的长方形的周长为40得,
∴,
由图2得没有覆盖的阴影部分的周长为,
故答案为:36.
23.
【难度】0.65
【分析】本题考查整式的加减运算的应用,算术平方根的应用.
设长方形的长为a,宽为b. 根据正方形的面积求得a,b,然后根据图中等量关系列代数式求值即可.
【详解】解:设长方形的长为a,宽为b.
因为面积为17的正方形卡片可知,,
解得:,,
所以未被长方形卡片覆盖的A区域与B区域的周长和为:
.
故答案为:.
24.4
【难度】0.85
【分析】本题考查了整式的加减的应用,根据周长的定义列出代数式计算即可得出答案,采用数形结合的思想是解此题的关键.
【详解】解:由图可得:
周长之差为:
,
故答案为:.
25.
【难度】0.65
【分析】通过两点间的距离比求出数轴上刻度“”与刻度“”之间的距离,进而求刻度“”在数轴对应的数及符号,最后通过“左加右减”即可求解.
本题主要考查了数轴与刻度尺,解题关键是求出一个单位长度代表多少厘米.
【详解】解:因为刻度尺上的刻度“”和“”分别对应数轴上的和,
∴刻度尺上刻度“”与刻度“”之间的距离是,是刻度尺上刻度“”与刻度“”之间的距离的倍;
而数轴上刻度“”和“”之间的数轴距离是,
所以数轴上刻度“”与刻度“”之间的距离是,由于刻度“”在数轴的左边,属于负数,所以对应的数应为,向右平移个单位后为.
故刻度尺上对应数轴上的数为.
故答案为:.
26.B
【难度】0.85
【分析】本题考查数轴,有理数的减法与除法,圆周上表示数字0的点与数轴上表示的点重合,滚动到2023时,滚动了2025个单位长度,用2025除以4,余数即为重合点.
【详解】解:圆周上表示数字0的点与数轴上表示的点重合,
,
,
∴数轴上表示2023的点与圆周上表示1的点重合.
故选:B.
27.A
【难度】0.85
【分析】本题考查了数轴,绝对值等知识.理解为:数对应的点到两数1与两数在数轴上所对应的两点之间的距离之和为6.所以数对应的点在1到之间,整数有7个.
【详解】解:.
,
,,,,,0,1共7个整数.
故答案为:A.
28.0
【难度】0.85
【分析】圆周上的0点与重合,滚动到2023,圆滚动了2024个单位长度,用2024除以4,余数即为重合点.
【详解】解:圆周上的0点与重合,
,
,
圆滚动了506 周到2023,
圆周上的0与数轴上的2023重合,
故答案为:0.
【点睛】本题考查了数轴,找出圆运动的规律与数轴上的数字的对应关系是解决此类题目的关键.
29.
【难度】0.65
【分析】本题考查了数轴的应用,解题的关键是找出题目中的规律,根据发现的规律可以计算出数轴上对应的数.由题意知,每4次翻转为一个循环组依次循环,且矩形周长为8,计算2023被4除的余数即可求得答案.
【详解】解:由题意得:
第一次翻转,右边的点移动3个单位,
第二次翻转,右边的点移动1个单位,
第三次翻转,右边的点移动3个单位,
第四次翻转,右边的点移动1个单位,
翻转4次,为一个周期,
一个周期,右边的点移动8个单位,
,
右边的点移动,
,
故答案为:.
30.
【难度】0.85
【分析】先确定,翻转1次后,点B所对应的数为1;翻转4次后,点B所对应的数为;翻转7次后,点B所对应的数为,由于,从而可判断连续翻转次后,点B对应的数为.
【详解】解:∵点A、C对应的数分别为0和,
∴,
∵为等边三角形,
∴,
∵绕顶点按顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,翻转3次后,点B所对应的数为3,翻转4次后,点B所对应的数为;翻转7次后,点B所对应的数为,
而,
∴连续翻转次后,点B对应的数为.
故答案为:.
【点睛】本题考查了数轴:所有的有理数都可以用数轴上的点表示.也考查了等边三角形的定义和数字变换规律型问题的解决方法.
31.(1)8
(2)经过秒后,图形I与图形II并行(点P与点Q重合),此时点P表示的数为
(3)或
【难度】0.65
【分析】本题考查了数轴,一元一次方程的应用;
(1)根据数轴上两点间距离的求法计算即可;
(2)设运动时间为t,根据点P与点Q重合时表示的数相同,列方程求出时间t,进而可计算此时点P表示的数;
(3)由题意可知重叠部分为1个正方形,设运动时间为t,分情况讨论:当点P在点Q左侧时;当点P在点Q右侧时;分别根据重叠部分为1个正方形,列方程求出时间t,进而可计算此时点P表示的数.
【详解】(1)解:∵点A表示数,点B表示数3,
∴点A与点B的距离是,
故答案为:8;
(2)设运动时间为t,
由题意得:,
解得:,
此时点P表示的数为,
答:经过秒后,图形I与图形II并行(点P与点Q重合),此时点P表示的数为;
(3)∵重叠部分的面积与未重叠部分的面积之比为,
∴重叠部分为1个正方形,
设运动时间为t,
当点P在点Q左侧时,
由题意得:,
解得:,
此时点P表示的数为;
当点P在点Q右侧时,
由题意得:,
解得:
此时点P表示的数为:;
故答案为:或.
32.(1),
(2),
(3)
【难度】0.65
【分析】本题考查绝对值和算术平方根的非负性,数轴,一元一次方程的应用.
(1)根据绝对值和算术平方根的非负性求解即可;
(2)根据数轴上的点平移的变化规律即可解答;
(3)分两种情况讨论:点C是的美好点或点D是的美好点.根据“美好点”的定义列出方程,求解后结合进行取舍,即可解答.
【详解】(1)解:∵,,
且,
∴,,
∴,,
∴,;
故答案为:,
(2)解:∵点B表示的数是,向右平移个单位得到点C,
∴点C表示的数是,即,
∵点C向右平移个单位得到点D,
∴点D表示的数是,即.
故答案为:,
(3)解:若点C是的美好点,
则
解得:,
∴,,
∴,不合题意,舍去;
若点D是的美好点,
则
解得:,
∴,,
∴,符合题意.
综上所述,.
33.(1)5
(2)①或;②或1
【难度】0.65
【分析】此题考查了一元一次方程的实际应用-行程问题;有理数在数轴上的表示,数形结合和列出一元一次方程是解题的关键.
(1)先求点A的运动速度,然后根据点A,B的运动速度之比求点B的运动速度,进而得到点N的表示的数.
(2)①分两种情况:当 A,B两点向左运动时;当A,B两点向右运动时, 然后分别求点B表示的数.
②设运动t秒,根据点B所表示的数与点A所表示的数的和与差均为非负数,分两种情况:当 A,B两点向右运动时,点A所表示的数为,点B所表示的数为;当A点向右,B点向左运动时,点A所表示的数为,点B所表示的数为,然后列等式求解即可.
【详解】(1)解:∵点A从数1的位置经过4秒运动到点M, 点M表示的数为,
∴点A的运动速度为
∵点A,B的运动速度之比是,
∴点B的运动速度为1.
所以点N的表示的数为.
故答案为:5.
(2)①分两种情况:
当 A,B两点向左运动时, 点B表示的数为;
当A,B两点向右运动时, 点B表示的数为.
综上所述, 点B表示的数为或.
②设运动t秒,根据点B所表示的数与点A所表示的数的和与差均为非负数,分两种情况:
当 A,B两点向右运动时,点A所表示的数为,点B所表示的数为
所以,解得 .
,解得.
所以相应这段时间持续了秒 ;
当A点向右,B点向左运动时,点A所表示的数为,点B所表示的数为
所以,解得.
. 解得
所以相应这段时间持续了秒 .
综上所述, 这段时间持续了或1秒 .
34.(1);
(2)经过5或15秒,点P到点A与点B的距离相等;
(3)有7种移动方法;
(4)A和点B经过相同次数的移动后,不能同时到达原点O
【难度】0.4
【分析】(1)设,则,根据“A,B之间距离为15“列方程,可求出x,进而得到点A表示的数,点B表示的数;
(2)设经过t秒,点P到点A与点B的距离相等,列方程求解即可;
(3)设点B沿着数轴向左移动次,则向右移动次,可得,再分析即可;
(4)设点A向左移动次,向右移动次,则B移动次,可得:,设B向左移动次,向右移动了次,可得,结合移动次数为非负整数可得答案.
【详解】(1)解:设点B表示的数为x,则点A表示的数为,
则,
解得:,
∴点A表示的数为,点B表示的数为;
(2)设经过t秒,A对应的数为,P对应的数为,B对应的数为,而点P到点A与点B的距离相等,
则:即,
解得:或,
答:经过5或15秒,点P到点A与点B的距离相等;
(3)设点B沿着数轴向左移动次,则向右移动次,
∴,即,
解得:或,
当时,有1种移动方法,
当时,移动方式有左5(连续)右1,左4(连续)右1左1,左3(连续)右1左2(连续),左2(连续)右1左3(连续),左1右1左4(连续),右1左5(连续),
综上共有7种移动方法;
(4)不能,理由如下:
设点A向左移动次,向右移动次,则B移动次
∴,
解得:,
设B向左移动次,向右移动了次,
∴,
∴
∵,,都为正整数,
∴不符合题意,
∴A和点B经过相同次数的移动后,不能同时到达原点O.
【点睛】本题考查的是数轴上两点之间的距离,数轴上的动点问题,一元一次方程的应用,本题难度大,熟练的利用一元一次方程解题是关键.
35.(1);
(2)再行驶3秒或5秒钟两列火车行驶到车头相距6个单位长度;
(3)这个时间为秒,定值为6个单位.
【难度】0.65
【分析】(1)由题意可得,求出,即可求解;
(2)分两种情况,点在点的右侧或点在点的左侧,分别求解即可;
(3)由题意可得当在之间时,为定值,据此求解即可.
【详解】(1)解:由题意可得
∴,,解得,
即点表示的数为,点表示的数为,
之间的距离为;
(2)设经过秒钟,相距为6个单位,此时点表示的数为,点表示的数为,
当点在点的右侧,,解得
当在点的左侧时,,解得
即再行驶3秒或5秒钟两列火车行驶到车头相距6个单位长度;
(3)由题意可得,在线段上
∴
由为定值可得,为定值,
所以此时点在线段上,,
时间
即这个时间为秒,定值为6个单位.
【点睛】本题考查了两点的距离,数轴,绝对值和偶次方的非负性,知道数轴上任意两点之间的距离等于右边的数减去左边的数,熟练掌握行程问题的数量关系,时间等于路程除以速度,根据数形结合的思想理解和解决问题.
36.(1)132;6;61
(2)存在点M,使,点M对应的数为或
(3)当点P,Q停止运动时,点P所在的位置表示的数为,点P和点Q一共相遇了次
【难度】0.4
【分析】本题考查了数轴上的动点问题,数轴上两点间距离;
(1)根据可得,故可得的长度,再利用时间等于路程除以速度和,即可解答;再根据求得时间,即可得到相遇点表示的数;
(2)设点表示的数为,考虑两种情况,即点在点左边,点在点和点中间,再根据,列方程即可解答;
(3)求出点运动的时间,即可算出点运动的路程,再求出点的位置即可,再根据点来回次数,求得和点相遇次数.
熟练利用代数式表示动点表示的位置是解题的关键.
【详解】(1)解:根据,可得,,
,
(秒),
相遇的点为;
(2)解:设点表示的数为,
①当点在点左边时,
,,,
根据,可列方程,
解得;
②点在点和点中间时,
,,,
根据,可列方程,
解得;
综上所述,存在点M,使,点M对应的数为或;
(3)解:点运动的时间为(秒),
,
所以可得点总共往返6趟,且最后停止在处,
综上所述,点P和点Q一共相遇了7次.
37.(1)6;
(2)
(3)①;②;8
【难度】0.65
【分析】(1)根据数轴上两点间距离公式进行解答即可;
(2)①根据时间进行计算即可;
②设运动时间为,则运动后,点P表示的数为:,点Q表示的数,分两种情况:Q在P右侧时,Q在P左侧时,列出方程,求出t的值即可.
【详解】(1)解:点A和点B的距离是:;
点C对应的数是;
故答案为:6;.
(2)解:∵的距离长度为4,
∴速度差,
∴.
(3)解:①的距离为6,则的距离为2,的距离长度为4.
Q在P左侧时,时间秒;
故答案为:.
②∵点P与点Q的距离与点A与点B距离之比为,
∴此时,
∵,,
∴设运动时间为,则运动后,点P表示的数为:,点Q表示的数,
(i)Q在P右侧时,,
解得:,
则P点对应的数为.
(ii)Q在P左侧时,,
解得:,
则P点对应的数为.
综上分析可知,点P表示的数为或8.
【点睛】本题主要考查了数轴上两点间的距离,用数轴上点表示有理数,数轴上动点问题,一元一次方程的应用,解题的关键是熟练掌握数轴上两点间距离,注意分类讨论.
38.(1)10
(2)①;②或.
【难度】0.85
【分析】本题考查了数轴上两点之间的距离、一元一次方程、合并同类项.
(1)根据两点之间的距离公式计算即可;
(2)①根据两点之间的距离公式,得出,,再根据,列出一元一次方程,解出即可得出答案;
②根据题意,列出方程整理即可得出结论.
【详解】(1)解:∵当,时,
∴线段;
故答案为:10;
(2)解:①∵数轴上另有一点N对应着数n,点N在点A,B之间,,,
∴,,
又∵,
∴,
解得:,
∴数n是;
故答案为:;
②∵,
∴,
整理得或,
即或.
39.(1)2;(2)①-5,②-4.5和2.5;(3)1或2或3
【难度】0.65
【分析】(1)利用数轴的对称性可得答案;
(2)①先确定好折痕点对应的数,再利用距离相等可得答案;②利用数轴上、两点到折痕的距离为3.5,从而可得答案;
(3)分三种情况画出符合题意的图形,再利用对折的性质,逐一解答即可.
【详解】解:操作一,
(1)∵表示的点1与-1表示的点重合,
∴折痕为原点,
则-2表示的点与2表示的点重合,
故答案为:2;
操作二:
(2)∵折叠纸面,若使1表示的点与-3表示的点重合,
则折痕表示的点为-1,
①设3表示的点与数表示的点重合,
则,
则;
②∵数轴上、两点之间距离为7,
∴数轴上、两点到折痕-1的距离为3.5,
∵在的左侧,
则、两点表示的数分别是-4.5和2.5;
故答案为:①-5,②-4.5和2.5;
操作三:
(3)如图1,当时,
设,,,
,
则,
∴,,,
∴折痕处对应的点所表示的数是:,
如图2,当时,
设,,,
,
则,
∴,,,
∴折痕处对应的点所表示的数是:,
如图3,当时,
设,,,
,
则,
∴,,
∴折痕处对应的点所表示的数是:,
综上所述:则折痕处对应的点所表示的数可能是1或2或3.
故答案为:1或2或3.
【点睛】本题考查了实数和数轴的关系,及数轴上的折叠变换问题,明确①数轴上折叠后重合的点到折痕的距离相等,②数轴上任意两点的距离为两点坐标的绝对值;本题第三问有难度,采用了分类讨论的思想.
40.(1),,5
(2)3
(3)①28;②当时,的值随时间t的变化而变化;当时,的值为26.
【难度】0.4
【分析】(1)根据最大的负整数是 1,绝对值和偶次方具有非负性可求解;
(2)由题意容易得出折叠点表示的数是1,再根据与2的距离可得答案;
(3)①先表示出t秒后A、B、C表示的数,然后分别求出,,再代入计算即可得出结论;
②先表示出t秒后A、B、C表示的数,然后分别求出,,然后分A在B的左侧;A在B的右侧讨论,再代入计算即可得出结论.
【详解】(1)解:∵a,c满足与互为相反数,
∴,
∴,,
∴,,
∵b是最大的负整数,
∴;
故答案为:,,5;
(2)解:当与5重合时,折叠点是,
∴与点B重合的点表示的数为:,
故答案为:3;
(3)解:①t秒后,A表示的数为,B表示的数为,C表示的数,
∴,
,
∴
;
②秒后,A表示的数为,B表示的数为,C表示的数,
∴,
,
当A、B重合时,,解得,
当A在B的左侧,即时,,
∴
,
∴的值随时间t的变化而变化;
当A在B的右侧,即时,,
∴
;
综上,当时,的值随时间t的变化而变化;当时,的值为26.
41.(1),1
(2)的值为3
(3)①有重叠部分时持续的时间为1秒;②或
【难度】0.4
【分析】本题考查数轴上点的运动,一元一次方程的应用,解题关键是表示出运动后点表示的数.
(1)当时,根据路程速度时间及数轴上两点之间的距离即可求解;
(2)根据题意,可得点表示的数为,点表示的数为,再由点和点重合,建立方程求解即可得出答案;
(3)①分别求得点与点重合、点与点重合所需时间,求出两个时间差即可;②分两种情况:当点落在线段上时,当点落在线段上时,分别画出图形,根据题意建立方程求解即可得出答案.
【详解】(1)解:当时,点表示的数为,点表示的数为,
(2)由题意得:秒后,点表示的数为:,点表示的数为:,
∵点和点重合,
∴,
解得:,
∴的值为3;
(3)①由题意得:秒后,点表示的数为:,点表示的数为:,
当点与点重合时:,
解得:,
由(2)知:时,点与点重合,
∵(秒),
∴有重叠部分时持续的时间为1秒;
②当点落在线段上时,如图,
∵重叠部分长方形的周长是长方形的周长的一半,
∴,
∵,,,
∴,
解得:,
∴点所表示的数为;
当点落在线段上时,如图,
∵重叠部分长方形的周长是长方形的周长的一半,
∴,
∵,,,
∴,
解得:,
∴点所表示的数为;
综上所述,点所表示的数为或;
42.实践:(1);(2);(3)6;探案:(1);(2);(3)1或;应用:,;
【难度】0.65
【分析】实践:根据数轴上两点间距离公式进行求解即可;
探案:(1)根据数轴上两点间距离计算方法进行表示即可;
(2)根据绝对值的意义和数轴上两点间距离公式进行解答即可;
(3)解绝对值方程求出结果即可;
应用:根据数轴上两点距离公式和长方形面积公式求出和,然后进行比较大小即可.
【详解】解:实践:(1);
(2);
(3);
探案:(1)数轴上表示数与1的两点之间的距离可用符号语言记作;
故答案为:;
(2)的含义是数轴上表示数与的两点之间的距离;
故答案为:;
(3)∵,
∴,
解得:或;
故答案为:1或;
应用:,
,
∴
,
根据数轴可知,,
∴,
∴,
∴.
【点睛】本题主要考查了数轴上两点间距离,绝对值的意义,整式加减的应用,绝对值方程,数轴上点的特点,解题的关键是熟练掌握相关的知识,数形结合.
43.(1)
(2)①点在数轴上表示的数为;②或
【难度】0.4
【分析】(1)根据点表示的数和点与点的位置关系和距离求出点表示的数,再根据正方形的边长即可求出数轴上点表示的数;
(2)①根据点和点之间的距离以及运动速度求出两点相遇时的运动时间,即可求出相遇时点表示的数,再加上正方形的边长即可求出相遇时点在数轴上表示的数;
②由①可知相遇时点在数轴上表示的数,然后根据条件列出方程,求出满足条件时的运动时间,再根据运动时间即可求出点在数轴上表示的数.
【详解】(1)解:∵点表示的数为,点在点左边,且点与点的距离为;
∴点表示的数为:,
∵边长为的正方形在数轴上,
∴点在点左边,,
∴点表示的数为:,
故答案为:;
(2)①设P、B两点相遇时间为秒,
由题意得:,
解得:,
此时点表示的数为:,
∴相遇时点表示的数为:;
②由①可知:相遇时、表示的数为,点表示的数为,
即点与点重合,
设相遇后的运动时间为秒,
当点与点的距离等于点到点的距离时,,,
∴,
解得:或,
∴当时,点表示的数为:,
当时,点表示的数为:,
综上所述,此时在数轴上表示的数为或.
故答案为:或.
【点睛】本题考查用数轴上的点表示数,数轴上的动点问题,数轴上两点之间的距离,一元一次方程的应用,路程与速度之间的关系等知识点,正确理解题意并建立一元一次方程是解题的关键.
44.(1),;(2)①图见解析,;②见解析
【难度】0.4
【分析】(1)根据图1得到小正方形的对角线长,即可得出数轴上点A和点B表示的数
(2)根据长方形的面积得正方形的面积,即可得到正方形的边长,再画出图象即可;
(3)从原点开始画一个长是2,高是1的长方形,对角线长即是a,再用圆规以这个长度画弧,交数轴于点M,再把这个长方形向左平移3个单位,用同样的方法得到点N.
【详解】(1)由图1知,小正方形的对角线长是,
∴图2中点A表示的数是,点B表示的数是,
故答案是:,;
(2)①长方形的面积是5,拼成的正方形的面积也应该是5,
∴正方形的边长是,
如图所示:
故答案是:;
②如图所示:
【点睛】本题考查无理数的表示方法,解题的关键是理解题意,模仿题目中给出的解题方法进行求解.
45.(1);
(2)
(3),,,
【难度】0.65
【分析】此题主要考查了代数式求值,等式性质,绝对值的意义,解题的关键是掌握整体代入的思想.
(1)根据等式的性质即可求解;
(2)将原式变形,进而将已知代入求出即可;
(3)根据,得出,,再根据均为整数,即可求解.
【详解】(1)解:∵,
∴用的代数式表示为,
用的代数式表示为.
故答案为:;.
(2)解:,
.
(3)解:∵,
∴,,
,均为整数,,
∴,,,.
46.(1);2;5
(2)10或0
(3)①或;②,0,1,2,3,4
【难度】0.85
【分析】(1)先根据绝对值的非负性求出a、b的值,再根据两点间的距离公式求解;
(2)分类讨论解方程即可;
(3)①先根据x的范围去掉绝对值符号,再解方程即可;
②根据点M、点N之间时,最小,求出此时整数的值即可.
【详解】(1)解:∵,
∴,
∴A、B间的距离为,
故答案为:;
(2)解:
当时,,则;
当时,,则;
10或0.
(3)解:①当点在点左侧时,,
∴,
;
当点在点右侧时,,
,
∴,
;
综上所述,或.
②当点在点、之间时,,
的最小值为;
此时,,0,1,2,3,4.
【点睛】本题考查的是数轴上两点之间的距离,一元一次方程的应用,绝对值方程,数轴上点表示有理数,利用数形结合,方程思想解决问题是解本题的关键.
47.(1)3
(2);,2,或2,,
(3)11或4或10
【难度】0.65
【分析】(1)根据上述材料给出的方法计算其相应的最佳值为即可;
(2)按照三个数不同的顺序排列算出最佳值,由计算可以看出,要求得这些数列的最佳值的最小值;只有当前两个数的和的绝对值最小,最小只能为,由此得出答案即可;
(3)分情况算出对应的数值,建立方程求得a的数值即可.
【详解】(1)因为,,,
所以数列,,1的最佳值为3.
故答案为3.
(2)对于数列,,2,
因为,,,
所以数列,,2的最佳值为;
对于数列,2,,
因为,,,
所以数列,2,的最佳值为1;
对于数列2,,,
因为,,,
所以数列2,,的最佳值为1;
对于数列2,,,
因为,,,
所以数列2,,的最佳值为;
对于数列,,2,
因为,,,
所以数列,,2的最佳值为;
对于数列,2,,
因为,,,
所以数列,2, 4的最佳值为
∴数列的最佳值的最小值为,数列可以为:,2,或2,,.
故答案为,,2,或2,,.
(3)当时,则或,不合题意;
当,则或7;
当时,数列为,7,2,因为,,,
所以数列,7,2的最佳值为0,不符合题意;
当,则或10.
∴或4或10.
【点睛】此题考查数字的变化规律,理解新定义运算的方法是解决问题的关键.
48.(1);6;7
(2)7或
(3)
(4)2或3
(5);7
【难度】0.4
【分析】(1)由最大的负整数与绝对值的含义可得,的值,再求解两点之间的距离即可;
(2)由,再分三种情况讨论即可;
(3)由,再分三种情况讨论即可;
(4)由,可得或;再结合(2)可得结论;
(5)先求解,再结合绝对值的含义可得答案.
【详解】(1)解:∵点A表示的数a为最大的负整数,点B表示的数b在原点右侧,且绝对值为6,
∴,,
∴数轴上A,B两点之间的距离为;
(2)∵,
∴,
当时,,
∴,
当时,
∴,
方程无解;
当时,
∴,
解得:;
(3)∵,
当时,原式,
当时,
∴原式,
当时取得最小值;
当时,
∴原式;
综上:的最小值为;
(4)∵,
∴,
∴或;
当时,
结合(2)得:此时,
∴,
解得:,
当,结合(2)得:此时,
∴,
解得:,
综上:或;
(5)∵正实数c满足,
∴,
∴,
∵,
∴结合绝对值的含义可得当时,取得最小值,
最小值为:.
【点睛】本题考查的是数轴上两点之间的距离,绝对值的应用,一元一次方程的应用,利用平方根的含义解方程,二次根式的加减运算,掌握绝对值的几何意义是解本题的关键.
49.(1),12,
(2)①当t的值为2或8时,点P、Q两点到点A的距离相等;②
【难度】0.85
【分析】本题考查了一元一次方程的应用以及数轴,
(1)先利用非负性求出,即可表示出两点A、B对应的数,从而表示出点P表示的数;
(2)①先表示出,,再建立等式求解;②先表示出点Q表示的数,点M表示的数,再表示出,通过计算出,再根据与t无关即可求解.
【详解】(1)解:,
,,
,,
点A表示的数为,点B表示的数为12,点P表示的数,
故答案为:,12,.
(2)解:①,
由点P、Q两点到点A的距离相等,得,
,
解得:或8;
②点Q表示的数,点M表示的数.
则,,
,
∵式子的值不随时间t的变化而变化,
∴,
∴.
50.(1),,
(2)
(3)的取值是或3
【难度】0.65
【分析】(1)根据点在数轴上的位置,判断出式子的符号即可;
(2)先判断出式子的符号,再化简绝对值即可;
(3)分,,,,,和,,进行讨论求解即可.
【详解】(1)解:由图可知:,,
∴,,;
故答案为:,,;
(2)解:∵,,,
∴原式
;
(3)
,
①当,时,则
;
②当,时,则
;
③当,时,则
;
④当,时,则
.
综上所述:的取值是或3.
【点睛】本题考查利用数轴判断式子的符号,化简绝对值,整式的加减运算,利用数形结合和分类讨论的思想进行求解,是解题的关键.
51.(1)单位长度
(2)秒或秒
(3)正确,这个时间是秒,定值是个单位长度
【难度】0.4
【分析】(1)根据非负数的性质求出,,求差即可求解;
(2)根据时间=路程和÷速度和,设行驶秒钟两列火车行驶到车头和相距单位长度,列方程即可求解;
(3)由于,只需要是定值,从快车上乘客与慢车相遇到完全离开之间都满足是定值,依此分析即可求解.
【详解】(1)解:∵与互为相反数,
∴,
∴,,
解得:,,
∴此时刻快车头与慢车头之间相距(单位长度);
答:此时快车头与慢车头之间相距单位长度;
(2)设行驶秒钟两列火车行驶到车头和相距个单位长度,
两车相遇前可列方程为
,
解得,;
两车相遇后可列方程为
,
解得,;
答:再行驶秒或秒,两列火车行驶到车头和相距个单位长度;
(3)正确.理由如下:
∵六年级学生乘客在快车上,
∴,
当在之间时,是定值,即路程为,
∴行驶时间:(秒),
此时(单位长度),
∴这个时间是秒,定值是个单位长度.
【点睛】本题考查一元一次方程的应用,数轴、绝对值和偶次方的非负性,数轴上两点之间的距离,熟练掌握行程问题的等量关系:时间=路程÷速度,本题难度较大.方程思想和数形结合思想的应用是解题的关键.
52.(1)
(2)的值为5或
(3)①6,②420或440或460或
【难度】0.4
【分析】此题考查了绝对值的应用,解题的关键是理解“双倍关系值”的定义,熟练掌握绝对值的性质.
(1)根据“双倍关系值”的定义,求解即可;
(2)根据“双倍关系值”的定义,列方程,求解即可;
(3)①根据题意列出方程,再分为四种情况,分别讨论,根据绝对值的性质,把绝对值方程转化为常规方程进行解答便可;②分10种情况计算即可.
【详解】(1)解:由题意得:
,
故答案为:;
(2)解:由题意得:,即,
,
或,
解得:或,
的值为5或;
(3)解:①和关于1的“双倍关系值”为2,
,
分四种情况:
当时,,则;
当时,,则,即;
当时,,则;即;
当时,,则;
综上,的最大值为6,
故答案为:6;
②分10种情况:
1、当时,,解得,
由可得,,
……,
可得,
;
2、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
3、当时,,解得:或,
时,由,可得,此种情形不存在;
时,由,解得:或,
时,由,可得,此种情形不存在;
时,由,解得:或,
,
同理得:,
;
4、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
5、当,由,解得:或,
时,与矛盾,此种情形不存在;
,则,解得:或,
时,与矛盾,此种情形不存在;
,
同理:,,……,;
,即;
,即;
;
6、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
7、当,由,可得,解得:或,
时,与矛盾,此种情形不存在;
,
当时,由,可得,解得:或,
,与矛盾,此种情形不存在;
,
同理:,,……,;
;
8、当时,由,,……,
,,
或,
,则,与矛盾,此种情形不存在;
,,则,
或,
,则,与矛盾,此种情形不存在;
,
同理:,,……,;
,即;
,即;
同理可得:,…,,
,
;
9、当时,,解得,
由可得,,
……,
可得,
;
10、当时,,与矛盾,此种情形不存在;
综上所述:的值为420或440或460或,
故答案为:420或440或460或.
53.(1)2
(2)存在,或7
(3)或
【难度】0.85
【分析】本题主要考查非负性、两点之间的距离和一元一次方程的应用,
(1)根据相反数的意义,平方的非负性和绝对值的非负性求得a和b,利用两点之间距离即可求得;
(2)根据题意将距离之和表示为,利用数轴上两点之间距离去绝对值即可求得答案;
(3)先将第t分钟点A、B和P表示出,进一步求得和的距离,根据题意列出等式,解绝对值方程即可;
【详解】(1)解:∵,
∴,.
设P点对应的数为x,根据数轴得:,解得:,
则P对应的数为:2.
(2)根据题意得:,
由于点和点B之间距离为8,则点P只能位于A和B两侧,
当时,化简得:,即;
当时,化简得:,即;
故点P为或7时到点A和点B的距离之和为10.
(3)设第t分钟时,点P到点A、点B的距离相等.
∵A:,B:,P:,
∴.
.
∵,
∴.
则当,解得:;
当,解得:;
∴在分钟或分钟时距离相等.
54.(1)4;3
(2)
(3)
【难度】0.65
【分析】(1)根据数轴上、两点之间的距离计算便可;
(2)根据数轴上、两点之间的距离解答便可;当在表示数与2的两点及两点之间时,利用绝对值性质化简即可;
(3)利用分类讨论的数学思想解答本题.
【详解】(1)数轴上表示1和5两点之间的距离是,数轴上表示2和的两点之间的距离是,
故答案为:4;3
(2)数轴上表示x和两点之间的距离为.
∵x表示一个有理数,且,
∴,
故答案为:;
(3)由数轴可知,当时,取得最小值,
最小值是:,
此时,可取的整数值是:.
即的最小值是8,此时可取的整数值是:.
故答案为:.
【点睛】本题考查数轴上两点间的距离、绝对值,解题的关键是利用分类讨论的思想去绝对值符号.
同课章节目录
