数学:24.4中位线课件(华东师大版九年级上)
文档属性
| 名称 | 数学:24.4中位线课件(华东师大版九年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 495.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-22 19:24:00 | ||
图片预览



文档简介
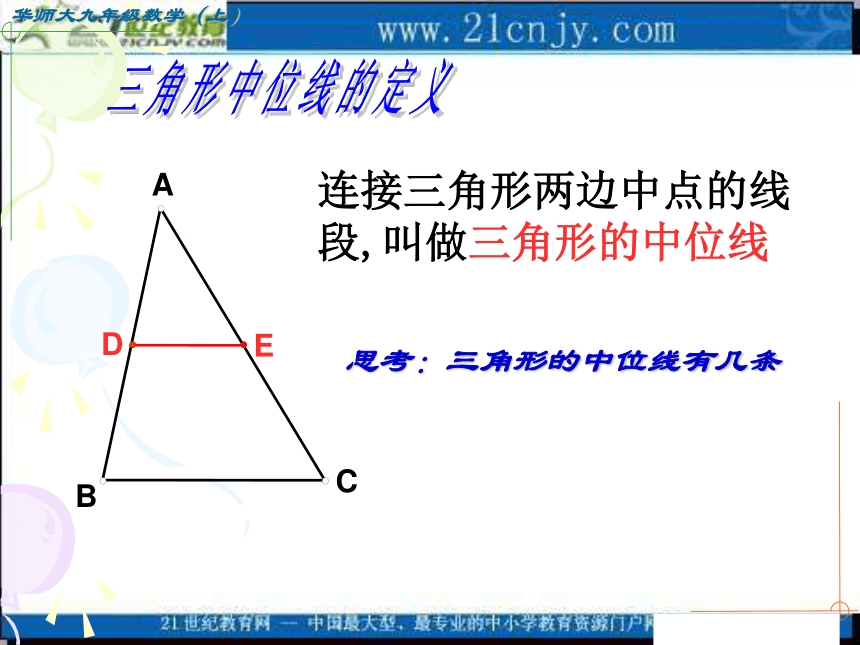
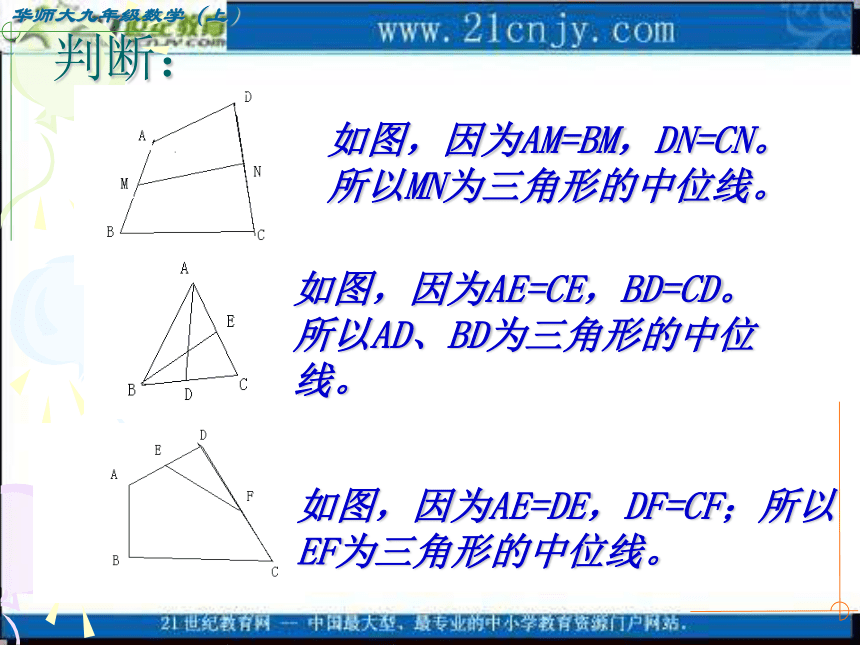
课件13张PPT。 如图, △ABC 中,点D、E分别是AB与AC的中点,证明:△ADE∽ △ABC猜想:DE∥BC,DE= BC.猜想DE与BC有怎样的位置关系和数量关系?为什么?CBAED连接三角形两边中点的线段,叫做三角形的中位线三角形中位线的定义思考:三角形的中位线有几条 课题 §24.4三角形的中位线判断:如图,因为AM=BM,DN=CN。所以MN为三角形的中位线。如图,因为AE=CE,BD=CD。所以AD、BD为三角形的中位线。如图,因为AE=DE,DF=CF;所以EF为三角形的中位线。
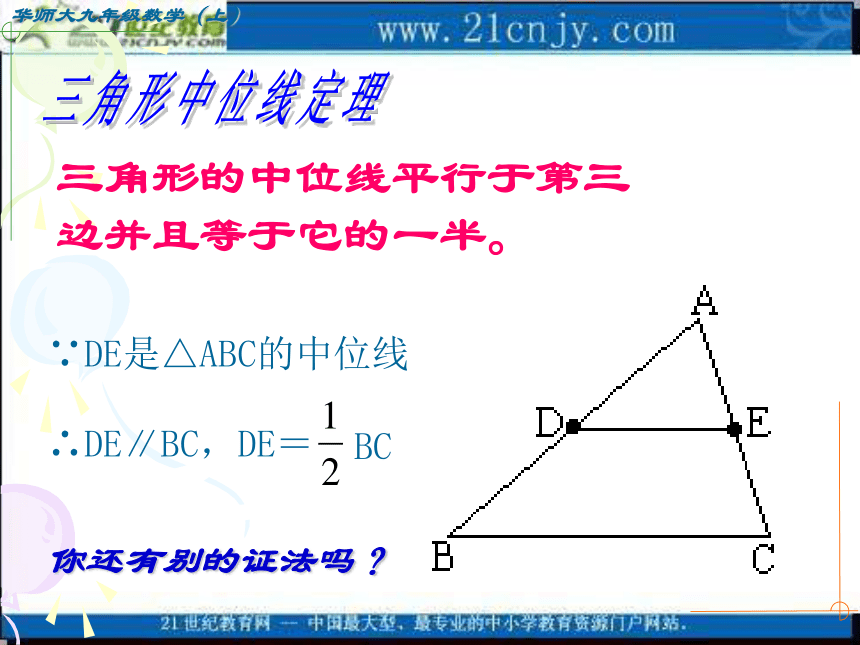
三角形中位线定理∵DE是△ABC的中位线
∴DE∥BC,DE=BC 三角形的中位线平行于第三边并且等于它的一半。你还有别的证法吗?已知:如果,点D、E、F分别是△ABC的三边的中点. (1)若AB=8cm,求EF的长;(2)若DE=5cm,求BC的长.(3)若增加M、N分别BD、BF的中点,问MN与AC有什么关系?为什么?练一练:(2)若△ABC的三条中位线围成的三角形周长为15cm, △ABC的周长是____。(1)若△ABC三边AB、AC、BC的长分别为8、6、 4,它的三条中位线围成的△DEF的周长_____。(3)若△ABC的三条中位线长分别为3、4、5,则△ABC的周长为 面积为 。 N
例1已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
(1)四边形ADEF是什么形状的四边形?并加以证明。
(2)DE与AF有什么关系?
(1)四边形ADEF是平行四边形.
证明 :
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 求证(1)四边形EFGH是平行四边形。
(2)请增加一个条件使得四边形ADFE为菱形。
(3) 请增加一个条件使得四边形ADFE为矩形。(4)能不能只增加一个条件使得四边形ADFE为正方形。
说一说你学到了什么?练习4 已知: 在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证∠PMN=∠PNM.布置作业1、练习 第1题
2、习题24.4 第1题 祝同学们学习愉快
三角形中位线定理∵DE是△ABC的中位线
∴DE∥BC,DE=BC 三角形的中位线平行于第三边并且等于它的一半。你还有别的证法吗?已知:如果,点D、E、F分别是△ABC的三边的中点. (1)若AB=8cm,求EF的长;(2)若DE=5cm,求BC的长.(3)若增加M、N分别BD、BF的中点,问MN与AC有什么关系?为什么?练一练:(2)若△ABC的三条中位线围成的三角形周长为15cm, △ABC的周长是____。(1)若△ABC三边AB、AC、BC的长分别为8、6、 4,它的三条中位线围成的△DEF的周长_____。(3)若△ABC的三条中位线长分别为3、4、5,则△ABC的周长为 面积为 。 N
例1已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
(1)四边形ADEF是什么形状的四边形?并加以证明。
(2)DE与AF有什么关系?
(1)四边形ADEF是平行四边形.
证明 :
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点. 求证(1)四边形EFGH是平行四边形。
(2)请增加一个条件使得四边形ADFE为菱形。
(3) 请增加一个条件使得四边形ADFE为矩形。(4)能不能只增加一个条件使得四边形ADFE为正方形。
说一说你学到了什么?练习4 已知: 在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证∠PMN=∠PNM.布置作业1、练习 第1题
2、习题24.4 第1题 祝同学们学习愉快
