1.2.2.1 全称量词命题与存在量词命题 课件 (共29 张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 1.2.2.1 全称量词命题与存在量词命题 课件 (共29 张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 622.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
1.2.2.1 全称量词命题与存在量词命题
1.了解命题的有关概念,能判断一个语句是否是命题.
2.理解全称量词、存在量词、全称量词命题、存在量词命题的概念及表示方法.(重点)
3.掌握判断全称量词命题、存在量词命题真假性的方法.(难点)
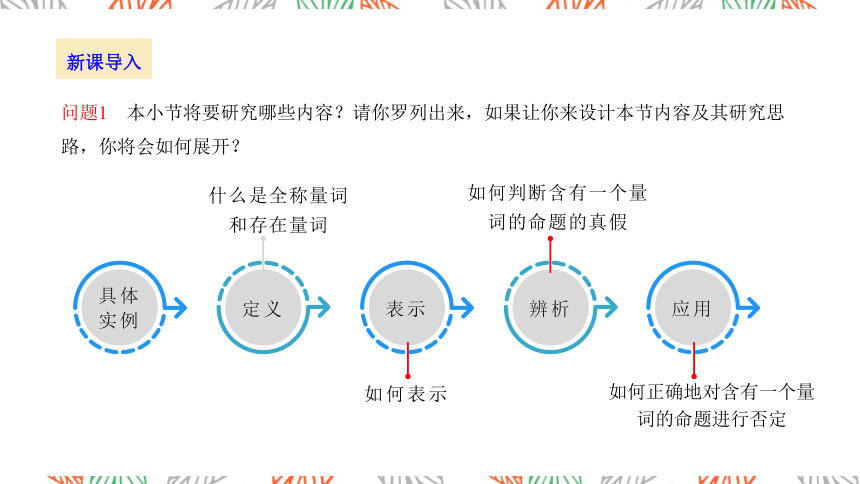
具体实例
定义
什么是全称量词和存在量词
表示
如何表示
应用
如何正确地对含有一个量词的命题进行否定
辨析
如何判断含有一个量词的命题的真假
问题1 本小节将要研究哪些内容?请你罗列出来,如果让你来设计本节内容及其研究思路,你将会如何展开?
新课导入
(1)x>3;
(2)2x+1是整数.
(1)(2)都不是命题,因为在这两个语句中,不知道变量x代表什么数,无法判断真假,所以它们不是命题.
问题2 下列语句是命题吗?为什么?
(1)x>3;
(2)2x+1是整数;
(3)对所有的x∈R,x>3;
(4)对任意一个x∈Z,2x+1是整数.
问题3 语句(3)(4)是命题吗?比较(1)和(3),(2)和(4),它们之间有什么关系?
√
√
(3)在(1)的基础上增加了短语“所有的”对变量x进行限定;
(4)在(2)的基础上增加了短语“任意一个”对变量x进行限定,
从而使(3)(4)成为可以判断真假的陈述句,所以(3)(4)是命题.
用一个短语对变量的取值范围进行限定,可以使类似“x>3”“2x+1是整数”的开语句成为一个命题,我们把这样的短语称为量词.
短语“所有的”、“任意一个”在逻辑中通常叫做全称量词,并用符号“ ”表示.
含有全称量词的命题,叫做全称量词命题.
通常,将含有变量x的语句用p(x),q(x),r(x),…,表示,变量x的取值范围用M表示.那么,全称量词命题“对M中任意一个x,p(x)成立”可用符号简记为: x∈M,p(x).
新知探究
常见的全称量词:
“每一个”“任意”“所有”“一切”“任给”等.
全称量词的含义:
在指定范围内,表示整体或者全部的含义.
新知探究
问题4 你还能说出哪些全称量词?全称量词的含义是什么?并试着举出几个全称量词命题.
全称量词命题举例:
(1)对任意的x∈R,x2+1>0;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
……
追问 全称量词命题可以简记为“ x∈M,p(x)”.对应下面的命题,“M”,“p(x)”分别指的是什么?
(1)“M”指的是R,“p(x)”指的是“x2+1>0”;
(2)“M”指的是“所有无理数”,“p(x)”指的是“x2也是无理数”;
(3)“M”指的是“所有一元二次方程”,“p(x)”指的是“方程都有实根”;
(1)对任意的x∈R,x2+1>0;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
(1)对任意的x∈R,x2+1>0;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
(1)是真命题;
对于 x∈R,总有x2+1≥1>0.所以,全称量词命题
“对任意的x∈R,x2+1>0”为真命题;
新知探究
问题5 请判断上述全称命题的真假,并说明理由.
(2)是假命题;
因为 是无理数, 是有理数.所以,全称量词命题“对任意一个无理数x,x2也是无理数”是假命题;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
问题5 请判断上述全称命题的真假,并说明理由.
(3)是假命题;
一元二次方程x2+x+1=0没有实根.所以,全称量词命题“所有的一元二次方程都有实根”是假命题.
(3)所有的一元二次方程都有实根;
问题5 请判断上述全称命题的真假,并说明理由.
追问 对给定的全称量词命题,如何判断它的真假?
如果对集合M中的每一个x,p(x)都成立,那么“ x∈M,p(x)”为真命题;
如果在集合M中存在一个x0,使得p(x0)不成立,那么“ x∈M,p(x)”为假命题.
新知探究
(1)2x+1=3;
(2)x能被2和3整除;
(3)存在一个x∈R,使2x+1=3;
(4)至少有一个x∈Z,x能被2和3整除.
(3)在(1)的基础上增加了短语“存在一个”对变量x进行限定;
不是
不是
是
是
(4)在(2)的基础上增加了短语“至少有一个”对变量x进行限定,
从而使(3)(4)成为可以判断真假的陈述句,
所以(3)(4)是命题.
新知探究
问题6 下列语句是命题吗?比较(1)和(3),(2)和(4),它们之间有什么关系?
短语“存在一个”、“至少有一个”在逻辑中通常叫做存在量词,并用符号“ ”表示.
含有存在量词的命题,叫做存在量词命题.
类比全称量词命题的符号表示,存在量词命题“存在M中的元素x,p(x)成立”可用符号简记为 x∈M,p(x).
新知探究
常见的存在量词:“存在一个”“至少有一个”“有些”“有一个”“对某些”“有的”等.
存在量词的含义:在指定范围内,表示个别或一部分的含义.
新知探究
问题7 你还能说出哪些存在量词?存在量词的含义是什么?并试着举出几个存在量词命题.
存在量词命题举例:
(1)有一个实数 ,使x2+1=0;
(2)存在一个无理数x,x2也是无理数;
(3)有些平行四边形是菱形;
新知探究
(1)有一个实数x,使x2+1=0;
(2)存在一个无理数x,x2也是无理数;
(3)有些平行四边形是菱形;
(1)是假命题;
对于 x∈R,总有x2+1>0,即不存在x∈R,使得x2+1=0.
所以,存在量词命题“有一个实数x,使x2+1=0”为假命题;
问题8 你能判断这些存在命题的真假吗?说明理由,并类比全称量词命题总结出存在量词命题真假的判断方法.
(2)存在一个无理数x,x2也是无理数;
(3)有些平行四边形是菱形;
(2)是真命题;
所以,存在量词命题“存在一个无理数x,x2也是无理数”是真命题;
因为 +1是无理数,( +1)2=3+ 是无理数.
新知探究
问题8 你能判断上述存在命题的真假吗?说明理由,并类比全称量词命题总结出存在量词命题真假的判断方法.
(3)有些平行四边形是菱形;
(3)是真命题;
对角线互相垂直的平行四边形是菱形.
所以,存在量词命题“有些平行四边形是菱形”是真命题.
新知探究
问题8 你能判断上述存在命题的真假吗?说明理由,并类比全称量词命题总结出存在量词命题真假的判断方法.
如果在集合M中存在一个x0,使得p(x0)成立,那么“ x∈M,p(x)”为真命题;
如果对集合M中每一个x,p(x)都不成立,那么“ x∈M,p(x)”为假命题.
新知探究
判断方法:
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
(1)对所有的实数a,b,关于x的方程ax+b=0恰有唯一解;
(2)所有的矩形都是平行四边形;
(3)至少有一个偶数是素数;
(4)存在x∈R,使x2+1<0.
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
目标检测
(1)对所有的实数a,b,关于x的方程ax+b=0恰有唯一解;
全称量词命题;
a,b∈R,关于x的方程ax+b=0恰有唯一解;
假命题;
因为当a=0,b≠0时,方程无解,
所以其为假命题;
目标检测
(2)所有的矩形都是平行四边形;
全称量词命题;
的矩形都是平行四边形;
真命题;
根据矩形的定义可知其为真命题;
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
目标检测
(3)至少有一个偶数是素数;
存在量词命题;
x是偶数,x是素数;
真命题;
所以“至少有一个偶数是素数”是真命题;
2是偶数,2也是素数,
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
(4)存在x∈R,使x2+1<0.
(4)存在量词命题;
x∈R,使x2+1<0;
假命题;
因为“ x∈R,x2+1>0”,
所以为假命题.
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
2.(1)将语句“x+y∈Z(整数集)”修改成全称量词命题,并使得该命题为真命题.
(2)将语句“a能被2整除”修改成存在量词命题,并使得该命题为假命题.
(1)对于 x,y∈Z,x+y∈Z;
(2) 奇数 ,a能被2整除.
回顾本节课所学知识,并用列表形式进行表示.
全称量词 存在量词
含义
举例
对应的命题
表示
判断
在指定范围内,表示整体或者全部.
在指定范围内,表示个别或一部分.
“所有的”、“每一个”、“任何一个”、“一切”等
“存在一个”、“至少有一个”、“有些”、“有的”等
全称量词命题
存在量词命题
对M中任意一个x,p(x)成立
存在M中元素x,p(x)成立
x∈M,p(x)
x∈M,p(x)
如果对集合M中的每一个x,p(x)都成立,那么“ x∈M,p(x) ”为真命题
如果在集合M中存在一个x0,使得p(x0)成立,那么“ x∈M,p(x) ”为真命题
如果在集合M中存在一个x0,使得p(x0)不成立,那么“ x∈M,p(x) ”为假命题
如果对集合M中每一个x,p(x)都不成立,那么“ x∈M,p(x) ”为假命题
1.2.2.1 全称量词命题与存在量词命题
1.了解命题的有关概念,能判断一个语句是否是命题.
2.理解全称量词、存在量词、全称量词命题、存在量词命题的概念及表示方法.(重点)
3.掌握判断全称量词命题、存在量词命题真假性的方法.(难点)
具体实例
定义
什么是全称量词和存在量词
表示
如何表示
应用
如何正确地对含有一个量词的命题进行否定
辨析
如何判断含有一个量词的命题的真假
问题1 本小节将要研究哪些内容?请你罗列出来,如果让你来设计本节内容及其研究思路,你将会如何展开?
新课导入
(1)x>3;
(2)2x+1是整数.
(1)(2)都不是命题,因为在这两个语句中,不知道变量x代表什么数,无法判断真假,所以它们不是命题.
问题2 下列语句是命题吗?为什么?
(1)x>3;
(2)2x+1是整数;
(3)对所有的x∈R,x>3;
(4)对任意一个x∈Z,2x+1是整数.
问题3 语句(3)(4)是命题吗?比较(1)和(3),(2)和(4),它们之间有什么关系?
√
√
(3)在(1)的基础上增加了短语“所有的”对变量x进行限定;
(4)在(2)的基础上增加了短语“任意一个”对变量x进行限定,
从而使(3)(4)成为可以判断真假的陈述句,所以(3)(4)是命题.
用一个短语对变量的取值范围进行限定,可以使类似“x>3”“2x+1是整数”的开语句成为一个命题,我们把这样的短语称为量词.
短语“所有的”、“任意一个”在逻辑中通常叫做全称量词,并用符号“ ”表示.
含有全称量词的命题,叫做全称量词命题.
通常,将含有变量x的语句用p(x),q(x),r(x),…,表示,变量x的取值范围用M表示.那么,全称量词命题“对M中任意一个x,p(x)成立”可用符号简记为: x∈M,p(x).
新知探究
常见的全称量词:
“每一个”“任意”“所有”“一切”“任给”等.
全称量词的含义:
在指定范围内,表示整体或者全部的含义.
新知探究
问题4 你还能说出哪些全称量词?全称量词的含义是什么?并试着举出几个全称量词命题.
全称量词命题举例:
(1)对任意的x∈R,x2+1>0;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
……
追问 全称量词命题可以简记为“ x∈M,p(x)”.对应下面的命题,“M”,“p(x)”分别指的是什么?
(1)“M”指的是R,“p(x)”指的是“x2+1>0”;
(2)“M”指的是“所有无理数”,“p(x)”指的是“x2也是无理数”;
(3)“M”指的是“所有一元二次方程”,“p(x)”指的是“方程都有实根”;
(1)对任意的x∈R,x2+1>0;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
(1)对任意的x∈R,x2+1>0;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
(1)是真命题;
对于 x∈R,总有x2+1≥1>0.所以,全称量词命题
“对任意的x∈R,x2+1>0”为真命题;
新知探究
问题5 请判断上述全称命题的真假,并说明理由.
(2)是假命题;
因为 是无理数, 是有理数.所以,全称量词命题“对任意一个无理数x,x2也是无理数”是假命题;
(2)对任意一个无理数x,x2也是无理数;
(3)所有的一元二次方程都有实根;
问题5 请判断上述全称命题的真假,并说明理由.
(3)是假命题;
一元二次方程x2+x+1=0没有实根.所以,全称量词命题“所有的一元二次方程都有实根”是假命题.
(3)所有的一元二次方程都有实根;
问题5 请判断上述全称命题的真假,并说明理由.
追问 对给定的全称量词命题,如何判断它的真假?
如果对集合M中的每一个x,p(x)都成立,那么“ x∈M,p(x)”为真命题;
如果在集合M中存在一个x0,使得p(x0)不成立,那么“ x∈M,p(x)”为假命题.
新知探究
(1)2x+1=3;
(2)x能被2和3整除;
(3)存在一个x∈R,使2x+1=3;
(4)至少有一个x∈Z,x能被2和3整除.
(3)在(1)的基础上增加了短语“存在一个”对变量x进行限定;
不是
不是
是
是
(4)在(2)的基础上增加了短语“至少有一个”对变量x进行限定,
从而使(3)(4)成为可以判断真假的陈述句,
所以(3)(4)是命题.
新知探究
问题6 下列语句是命题吗?比较(1)和(3),(2)和(4),它们之间有什么关系?
短语“存在一个”、“至少有一个”在逻辑中通常叫做存在量词,并用符号“ ”表示.
含有存在量词的命题,叫做存在量词命题.
类比全称量词命题的符号表示,存在量词命题“存在M中的元素x,p(x)成立”可用符号简记为 x∈M,p(x).
新知探究
常见的存在量词:“存在一个”“至少有一个”“有些”“有一个”“对某些”“有的”等.
存在量词的含义:在指定范围内,表示个别或一部分的含义.
新知探究
问题7 你还能说出哪些存在量词?存在量词的含义是什么?并试着举出几个存在量词命题.
存在量词命题举例:
(1)有一个实数 ,使x2+1=0;
(2)存在一个无理数x,x2也是无理数;
(3)有些平行四边形是菱形;
新知探究
(1)有一个实数x,使x2+1=0;
(2)存在一个无理数x,x2也是无理数;
(3)有些平行四边形是菱形;
(1)是假命题;
对于 x∈R,总有x2+1>0,即不存在x∈R,使得x2+1=0.
所以,存在量词命题“有一个实数x,使x2+1=0”为假命题;
问题8 你能判断这些存在命题的真假吗?说明理由,并类比全称量词命题总结出存在量词命题真假的判断方法.
(2)存在一个无理数x,x2也是无理数;
(3)有些平行四边形是菱形;
(2)是真命题;
所以,存在量词命题“存在一个无理数x,x2也是无理数”是真命题;
因为 +1是无理数,( +1)2=3+ 是无理数.
新知探究
问题8 你能判断上述存在命题的真假吗?说明理由,并类比全称量词命题总结出存在量词命题真假的判断方法.
(3)有些平行四边形是菱形;
(3)是真命题;
对角线互相垂直的平行四边形是菱形.
所以,存在量词命题“有些平行四边形是菱形”是真命题.
新知探究
问题8 你能判断上述存在命题的真假吗?说明理由,并类比全称量词命题总结出存在量词命题真假的判断方法.
如果在集合M中存在一个x0,使得p(x0)成立,那么“ x∈M,p(x)”为真命题;
如果对集合M中每一个x,p(x)都不成立,那么“ x∈M,p(x)”为假命题.
新知探究
判断方法:
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
(1)对所有的实数a,b,关于x的方程ax+b=0恰有唯一解;
(2)所有的矩形都是平行四边形;
(3)至少有一个偶数是素数;
(4)存在x∈R,使x2+1<0.
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
目标检测
(1)对所有的实数a,b,关于x的方程ax+b=0恰有唯一解;
全称量词命题;
a,b∈R,关于x的方程ax+b=0恰有唯一解;
假命题;
因为当a=0,b≠0时,方程无解,
所以其为假命题;
目标检测
(2)所有的矩形都是平行四边形;
全称量词命题;
的矩形都是平行四边形;
真命题;
根据矩形的定义可知其为真命题;
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
目标检测
(3)至少有一个偶数是素数;
存在量词命题;
x是偶数,x是素数;
真命题;
所以“至少有一个偶数是素数”是真命题;
2是偶数,2也是素数,
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
(4)存在x∈R,使x2+1<0.
(4)存在量词命题;
x∈R,使x2+1<0;
假命题;
因为“ x∈R,x2+1>0”,
所以为假命题.
1.下列命题中,哪些是全称量词命题,哪些是存在量词命题.用符号“ ”或“ ”表示下面的命题,并判断其真假.
2.(1)将语句“x+y∈Z(整数集)”修改成全称量词命题,并使得该命题为真命题.
(2)将语句“a能被2整除”修改成存在量词命题,并使得该命题为假命题.
(1)对于 x,y∈Z,x+y∈Z;
(2) 奇数 ,a能被2整除.
回顾本节课所学知识,并用列表形式进行表示.
全称量词 存在量词
含义
举例
对应的命题
表示
判断
在指定范围内,表示整体或者全部.
在指定范围内,表示个别或一部分.
“所有的”、“每一个”、“任何一个”、“一切”等
“存在一个”、“至少有一个”、“有些”、“有的”等
全称量词命题
存在量词命题
对M中任意一个x,p(x)成立
存在M中元素x,p(x)成立
x∈M,p(x)
x∈M,p(x)
如果对集合M中的每一个x,p(x)都成立,那么“ x∈M,p(x) ”为真命题
如果在集合M中存在一个x0,使得p(x0)成立,那么“ x∈M,p(x) ”为真命题
如果在集合M中存在一个x0,使得p(x0)不成立,那么“ x∈M,p(x) ”为假命题
如果对集合M中每一个x,p(x)都不成立,那么“ x∈M,p(x) ”为假命题
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
