1.4.1 一元二次函数 课件(共25张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 1.4.1 一元二次函数 课件(共25张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 920.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
1.4.1 一元二次函数
1.理解函数y=ax2(a≠0)与y=(x-h)2+k(a≠0)及y=ax2+bx+c(a≠0)的图象之间的关系.
2.掌握二次函数的概念、表达式、图象与性质.
3.会用配方法解决有关问题、能熟练地求二次函数的最值.
函数 开口方向 对称轴 顶点坐标
请同学们完成下表:
新课导入
思考:
规律探究
在同一个坐标系下画出下列函数图像:
探索发现
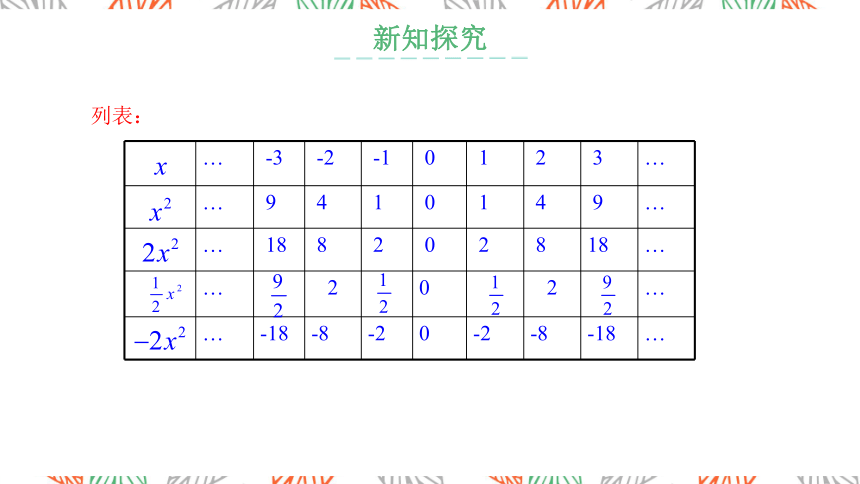
列表:
… -3 -2 -1 0 1 2 3 …
… 9 4 1 0 1 4 9 …
… 18 8 2 0 2 8 18 …
… 2 0 2 …
… -18 -8 -2 0 -2 -8 -18 …
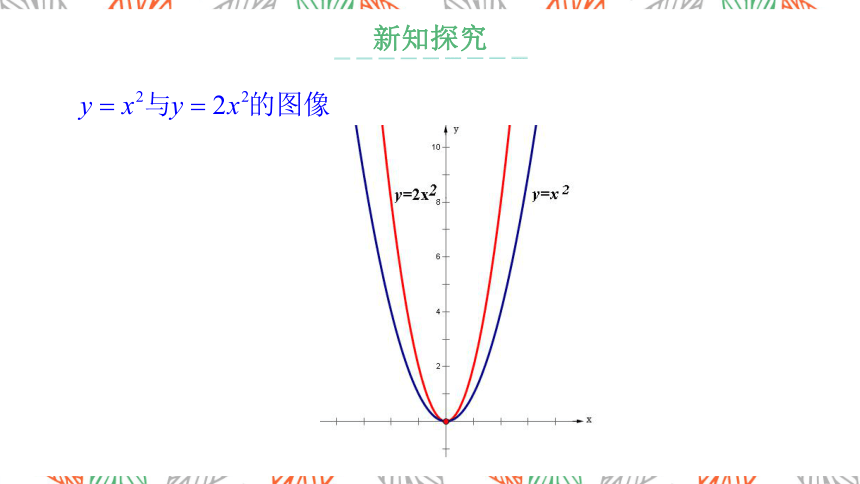
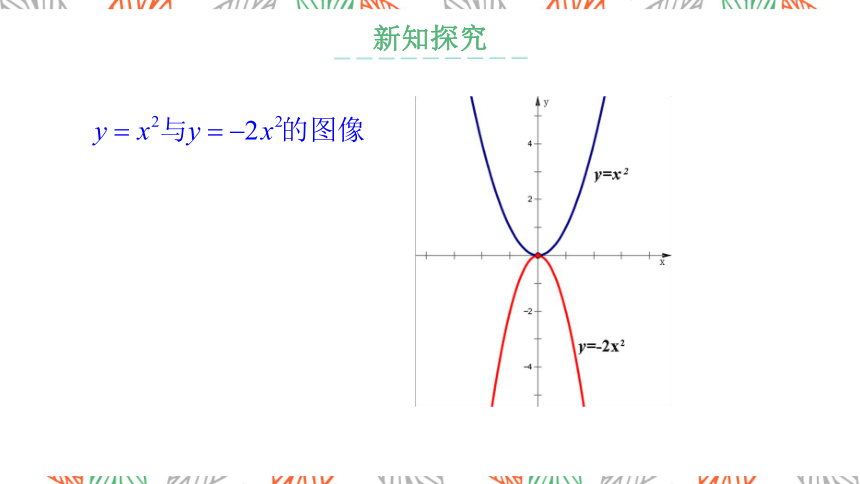
1.二次函数 的图像可由 的图像各点的纵坐标变为原来的 a 倍得到
2.a决定了图像的开口方向:a>0开口向上,a<0开口向下
3.a决定了图像在同一直角坐标系中的开口大小:
|a|越小,图像开口就越大
抽象概括
1.下列二次函数图像开口,按从小到大的顺序排列为
________________
(4),(2),(3),(1)
练一练:
, ,
,
说一说:这四个函数图像之间的关系,它们是进行了怎样的平移得到的?
规律探究
o
y
x
x=1
y=3x2+2
y=3x2
y=3(x-1)2
2
1
y=3(x-1)2+2
函数 的图像
函数 的图像
函数 的图像
函数 的图像
向上平移
2个单位
向右平移
1个单位
向右平移1个单位
向上平移2个单位
对称轴:y轴
开口方向:向上
顶点:(0,0)
对称轴:y轴
开口方向:向上
顶点: (0,2)
对称轴:x=1
开口方向:向上
顶点:(1,0)
对称轴:x=1 开口方向:向上 顶点:(1,2)
h=1>0
k=2>0
k=2>0
h=1>0
二次函数y=a(x-h) +k与y=ax 的关系
y=ax
(a≠0)
y=ax +k
(a≠0)
y=a(x-h) +k
(a≠0)
y=a(x-h)
(a≠0)
沿对称轴上(下)
平移|k|个单位
再向右(左)平移|h|个单位
沿对称轴上(下)
平移|k|个单位
沿x轴右(左)
平移|h|个单位
a>0时开口向上
a<0时开口向下
k>0时向上平移
k<0时向下平移
h>0时向右平移
h<0时向左平移
对于二次函数 (a≠0)的图像
抽象概括
回忆:二次函数y=ax2+bx+c(a≠0)的图像和性质
将二次函数y=ax2+bx+c(a≠0)配成y=a(x+h)2+k
抛物线 y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
顶点坐标
对称轴
开口方向
增减性
最值
向上
向下
二次函数y=ax2+bx+c(a≠0)的图像和性质
二次函数的性质可以通过下图直观表示出来
开口方向,顶点坐标,对称轴,单调性,最大值或最少值及图像
配方
2.把下列二次函数配方
练一练:
例2 将函数y=-3x2-6x+1配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.
解 : y=-3x2-6x+1=-3(x+1)2+4.
开口方向:
顶点坐标:
对称轴为:
单调区间:
最大值是:
向下
(-1,4)
x+1=0(或x=-1)
在区间(-∞,-1]上是增加的,
在区间[-1,+∞)上是减少的
4.
画图
y
4
3
2
1
-1
-2
-1
1
x
采用描点法
顶点A(-1,4)
(-1,4)A
D
B
C
与y轴的交点D(0,1)
E
再取点E(-2,1)
在配方后选取函数的关键点,使画图的操作更简便,图像更精确
3.已知函数f(x)=2x2-3x+1
(1)求这个函数图像的顶点坐标和对称轴;
(2)求这个函数的最小值;
(3) 试比较f(-1)和f(1)的大小.
练一练:
1.函数f(x)=x2+4ax+2在区间(-∞,6]上是减少的,则a的取值范围是( )
A、a≥3 B、a≤3
C、a≥-3 D、a≤-3
D
2.已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上是增加的,
则f(x)在[1,2]上的值域____________.
[21,49]
开口方向,顶点坐标,对称轴,单调性,最大值或最小值
配方
选取关键点
画图
求解最值问题
1.4.1 一元二次函数
1.理解函数y=ax2(a≠0)与y=(x-h)2+k(a≠0)及y=ax2+bx+c(a≠0)的图象之间的关系.
2.掌握二次函数的概念、表达式、图象与性质.
3.会用配方法解决有关问题、能熟练地求二次函数的最值.
函数 开口方向 对称轴 顶点坐标
请同学们完成下表:
新课导入
思考:
规律探究
在同一个坐标系下画出下列函数图像:
探索发现
列表:
… -3 -2 -1 0 1 2 3 …
… 9 4 1 0 1 4 9 …
… 18 8 2 0 2 8 18 …
… 2 0 2 …
… -18 -8 -2 0 -2 -8 -18 …
1.二次函数 的图像可由 的图像各点的纵坐标变为原来的 a 倍得到
2.a决定了图像的开口方向:a>0开口向上,a<0开口向下
3.a决定了图像在同一直角坐标系中的开口大小:
|a|越小,图像开口就越大
抽象概括
1.下列二次函数图像开口,按从小到大的顺序排列为
________________
(4),(2),(3),(1)
练一练:
, ,
,
说一说:这四个函数图像之间的关系,它们是进行了怎样的平移得到的?
规律探究
o
y
x
x=1
y=3x2+2
y=3x2
y=3(x-1)2
2
1
y=3(x-1)2+2
函数 的图像
函数 的图像
函数 的图像
函数 的图像
向上平移
2个单位
向右平移
1个单位
向右平移1个单位
向上平移2个单位
对称轴:y轴
开口方向:向上
顶点:(0,0)
对称轴:y轴
开口方向:向上
顶点: (0,2)
对称轴:x=1
开口方向:向上
顶点:(1,0)
对称轴:x=1 开口方向:向上 顶点:(1,2)
h=1>0
k=2>0
k=2>0
h=1>0
二次函数y=a(x-h) +k与y=ax 的关系
y=ax
(a≠0)
y=ax +k
(a≠0)
y=a(x-h) +k
(a≠0)
y=a(x-h)
(a≠0)
沿对称轴上(下)
平移|k|个单位
再向右(左)平移|h|个单位
沿对称轴上(下)
平移|k|个单位
沿x轴右(左)
平移|h|个单位
a>0时开口向上
a<0时开口向下
k>0时向上平移
k<0时向下平移
h>0时向右平移
h<0时向左平移
对于二次函数 (a≠0)的图像
抽象概括
回忆:二次函数y=ax2+bx+c(a≠0)的图像和性质
将二次函数y=ax2+bx+c(a≠0)配成y=a(x+h)2+k
抛物线 y=ax2+bx+c(a>0) y=ax2+bx+c(a<0)
顶点坐标
对称轴
开口方向
增减性
最值
向上
向下
二次函数y=ax2+bx+c(a≠0)的图像和性质
二次函数的性质可以通过下图直观表示出来
开口方向,顶点坐标,对称轴,单调性,最大值或最少值及图像
配方
2.把下列二次函数配方
练一练:
例2 将函数y=-3x2-6x+1配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.
解 : y=-3x2-6x+1=-3(x+1)2+4.
开口方向:
顶点坐标:
对称轴为:
单调区间:
最大值是:
向下
(-1,4)
x+1=0(或x=-1)
在区间(-∞,-1]上是增加的,
在区间[-1,+∞)上是减少的
4.
画图
y
4
3
2
1
-1
-2
-1
1
x
采用描点法
顶点A(-1,4)
(-1,4)A
D
B
C
与y轴的交点D(0,1)
E
再取点E(-2,1)
在配方后选取函数的关键点,使画图的操作更简便,图像更精确
3.已知函数f(x)=2x2-3x+1
(1)求这个函数图像的顶点坐标和对称轴;
(2)求这个函数的最小值;
(3) 试比较f(-1)和f(1)的大小.
练一练:
1.函数f(x)=x2+4ax+2在区间(-∞,6]上是减少的,则a的取值范围是( )
A、a≥3 B、a≤3
C、a≥-3 D、a≤-3
D
2.已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上是增加的,
则f(x)在[1,2]上的值域____________.
[21,49]
开口方向,顶点坐标,对称轴,单调性,最大值或最小值
配方
选取关键点
画图
求解最值问题
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
