2.1 生活中的变量关系 课件 (共17张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 2.1 生活中的变量关系 课件 (共17张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-23 22:32:51 | ||
图片预览





文档简介
(共17张PPT)
2.1 生活中的变量关系
1.了解生活中两个变量之间的依赖关系、函数关系.
2. 能辨析依赖关系与函数关系的区别与联系.
3.理解分段函数的概念,能够写出分段函数的解析式,画出其图象.
情景导入——乌鸦喝水
观看视频,你发现了哪些量不可以改变?哪些量可以改变?
(1)瓶口的大小不可以改变,水的数量也不能改变.
(2)瓶中水的高度可以改变,石块的数量可以改变,投的石块越多,水面越高.
复习回顾——函数关系
在初中你学过哪些函数?
正比例函数:y=kx (k≠0)
反比例函数:y=k/x (k≠0)
一次函数:y=kx+b (k≠0)
二次函数:
它们都表示了自变量x与函数值y之间的一种对应关系,是解析式表示的函数.
探究1:依赖关系
思考:V,h,w之间是否具有某种关系?
情景1 :如图是某高速公路加油站的图片,加油站在地下常用圆柱体储油罐储存汽油等燃料. 储油罐的长度 d、截面半径 r 是常量;油面高度 h、油面宽度 w、储油量 V 是变量.
结论:储油量 V 与油面高度 h 存在着依赖关系,
也与油面宽度 w 存在着依赖关系;
油面高度 h 的每一个取值,都有唯一的储油量 V 和它对应;
每一个油面宽度 w 的值,却对应着两个储油量 V .
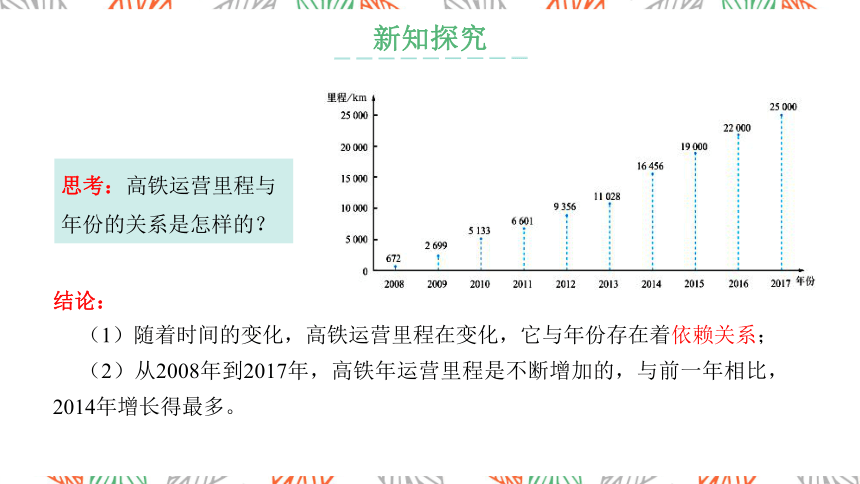
思考:高铁运营里程与年份的关系是怎样的?
情景2 :自2008年京津城际列车开通运营以来,高速铁路在中国大陆迅猛发展.截至2017年年底,中国高铁运营里程突破25000km.图中表示的是中国高铁年运营里程的变化.
结论:
(1)随着时间的变化,高铁运营里程在变化,它与年份存在着依赖关系;
(2)从2008年到2017年,高铁年运营里程是不断增加的,与前一年相比,2014年增长得最多。
思考:高铁运营里程与年份的关系是怎样的?
归纳总结
在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会随之发生变化,那么就称这两个变量具有依赖关系.
探究2:函数关系
函数概念中需注意:
凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都唯一确定的值和它对应”。
在初中数学中,函数的定义如下:
如果在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,那么y就是x的函数,其中x是自变量,y是因变量.
表示两个变量关系的函数的代数式,叫函数解析式.
如在例1中,储油量V是油面高度h的函数,但不是油面宽度w的函数.
依赖关系与函数关系的区别与联系
函数关系一定是依赖关系,而依赖关系不一定是函数关系.要确定变量的函数关系,需先分清谁是自变量,谁是因变量.
并非所有依赖关系的两个变量都有函数关系,只有满足对于其中一个变量的每一个值,另一个变量都有唯一确定的值时,才称它们之间有函数关系.
深入研究:
巩固练习
1.下列说法不正确的是( )
A.依赖关系不一定是函数关系
B.函数关系是依赖关系
C.如果变量m是变量n的函数,那么变量n也是变量m的函数
D.如果变量m是变量n的函数,那么变量n不一定是变量m的函数
环节二——函数关系
情景3 :弹簧的伸长量x与弹力y满足函数关系y=kx,其中k为劲度系数
说明:
对于变量“伸长量x”的每一个值,变量“弹力y”都有唯一确定的值和它对应,弹力y是伸长量x的函数.
说明:
对于变量“气压”的每一个值,变量“沸点”都有唯一确定的值和它对应,沸点是气压的函数.
情景4 :如表,记录了几个不同气压下水的沸点:
探究2:函数关系
说明:
图中反映的都是对于“时间”的每一个值,都有唯一确定的“气温”值和它对应,所以每一条曲线都表示了一个函数关系.
情景5 :绿化可以改变小环境气候某市有甲、乙两个气温观测点,观测点甲的绿化优于观测点乙,图中是这两个观测点某一天的气温曲线图.
探究3:分段函数
情景6 :国内某快递公司邮寄普通货物限重 30 kg,从 A 城市到 B 城市的快递资费标准是:质量 1 kg及以下收费 12 元,以后质量每增加 1 kg收费增加 8 元,质量不足1 kg 按 1 kg 计算.
试一试:请写出邮件的质量 m kg 与邮资 M 元的函数解析式,并画出局部图象.
解:依题意知邮件的质量 m kg与邮资M 元的函数解析式为:
O
1
2
3
4
5
12
20
36
28
44
M /元
m / kg
函数 M 局部图象
形如上述函数,在自变量的不同取值范围内,有不同的对应法则,需要用不同的解析式来表示的函数叫作分段函数.
本节课你学到了哪些知识?
2.1 生活中的变量关系
1.了解生活中两个变量之间的依赖关系、函数关系.
2. 能辨析依赖关系与函数关系的区别与联系.
3.理解分段函数的概念,能够写出分段函数的解析式,画出其图象.
情景导入——乌鸦喝水
观看视频,你发现了哪些量不可以改变?哪些量可以改变?
(1)瓶口的大小不可以改变,水的数量也不能改变.
(2)瓶中水的高度可以改变,石块的数量可以改变,投的石块越多,水面越高.
复习回顾——函数关系
在初中你学过哪些函数?
正比例函数:y=kx (k≠0)
反比例函数:y=k/x (k≠0)
一次函数:y=kx+b (k≠0)
二次函数:
它们都表示了自变量x与函数值y之间的一种对应关系,是解析式表示的函数.
探究1:依赖关系
思考:V,h,w之间是否具有某种关系?
情景1 :如图是某高速公路加油站的图片,加油站在地下常用圆柱体储油罐储存汽油等燃料. 储油罐的长度 d、截面半径 r 是常量;油面高度 h、油面宽度 w、储油量 V 是变量.
结论:储油量 V 与油面高度 h 存在着依赖关系,
也与油面宽度 w 存在着依赖关系;
油面高度 h 的每一个取值,都有唯一的储油量 V 和它对应;
每一个油面宽度 w 的值,却对应着两个储油量 V .
思考:高铁运营里程与年份的关系是怎样的?
情景2 :自2008年京津城际列车开通运营以来,高速铁路在中国大陆迅猛发展.截至2017年年底,中国高铁运营里程突破25000km.图中表示的是中国高铁年运营里程的变化.
结论:
(1)随着时间的变化,高铁运营里程在变化,它与年份存在着依赖关系;
(2)从2008年到2017年,高铁年运营里程是不断增加的,与前一年相比,2014年增长得最多。
思考:高铁运营里程与年份的关系是怎样的?
归纳总结
在某变化过程中有两个变量,如果其中一个变量的值发生了变化,另一个变量的值也会随之发生变化,那么就称这两个变量具有依赖关系.
探究2:函数关系
函数概念中需注意:
凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值,变量y都唯一确定的值和它对应”。
在初中数学中,函数的定义如下:
如果在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,那么y就是x的函数,其中x是自变量,y是因变量.
表示两个变量关系的函数的代数式,叫函数解析式.
如在例1中,储油量V是油面高度h的函数,但不是油面宽度w的函数.
依赖关系与函数关系的区别与联系
函数关系一定是依赖关系,而依赖关系不一定是函数关系.要确定变量的函数关系,需先分清谁是自变量,谁是因变量.
并非所有依赖关系的两个变量都有函数关系,只有满足对于其中一个变量的每一个值,另一个变量都有唯一确定的值时,才称它们之间有函数关系.
深入研究:
巩固练习
1.下列说法不正确的是( )
A.依赖关系不一定是函数关系
B.函数关系是依赖关系
C.如果变量m是变量n的函数,那么变量n也是变量m的函数
D.如果变量m是变量n的函数,那么变量n不一定是变量m的函数
环节二——函数关系
情景3 :弹簧的伸长量x与弹力y满足函数关系y=kx,其中k为劲度系数
说明:
对于变量“伸长量x”的每一个值,变量“弹力y”都有唯一确定的值和它对应,弹力y是伸长量x的函数.
说明:
对于变量“气压”的每一个值,变量“沸点”都有唯一确定的值和它对应,沸点是气压的函数.
情景4 :如表,记录了几个不同气压下水的沸点:
探究2:函数关系
说明:
图中反映的都是对于“时间”的每一个值,都有唯一确定的“气温”值和它对应,所以每一条曲线都表示了一个函数关系.
情景5 :绿化可以改变小环境气候某市有甲、乙两个气温观测点,观测点甲的绿化优于观测点乙,图中是这两个观测点某一天的气温曲线图.
探究3:分段函数
情景6 :国内某快递公司邮寄普通货物限重 30 kg,从 A 城市到 B 城市的快递资费标准是:质量 1 kg及以下收费 12 元,以后质量每增加 1 kg收费增加 8 元,质量不足1 kg 按 1 kg 计算.
试一试:请写出邮件的质量 m kg 与邮资 M 元的函数解析式,并画出局部图象.
解:依题意知邮件的质量 m kg与邮资M 元的函数解析式为:
O
1
2
3
4
5
12
20
36
28
44
M /元
m / kg
函数 M 局部图象
形如上述函数,在自变量的不同取值范围内,有不同的对应法则,需要用不同的解析式来表示的函数叫作分段函数.
本节课你学到了哪些知识?
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
